机场群可达性空间布局优化模型
陈一村, 赵 健, 陶西贵, 唐振宇, 冯进技, 贾艺凡
(军事科学院 国防工程研究院, 北京 100850)
随着我国社会经济和国防建设发展需要,机场作为城市航空运输和作战保障的关键基础设施,其数量规模正不断扩大,已初步形成了以大型枢纽机场为核心、以中型骨干和小型节点机场为补充的机场群体系[1-3]。相关数据显示[4],2020年,我国已有民用运输机场238个,到2035年,国家民用运输机场预计达到400个左右。然而,由于机场建管分离的管理模式和持续高强度建设的影响,小型机场因客运流量少出现了设施闲置、资源浪费等现象,大型枢纽机场因超饱和运行,服务质量和满意度进一步下滑,总体上造成机场群体系内的竞争协同关系呈恶化趋势发展。例如,2019年民航生产量统计公报显示[5],旅客吞吐量低于200万人次/年的中小机场占我国机场总数近70%,但这近70%的机场完成旅客吞吐量只占境内机场旅客总吞吐量的6.8%。因此,机场群体系利用不充分、不均衡问题逐渐突出,已成为困扰其建设发展的重大难题,亟需更合理、高效的建设发展方式。
为解决机场群体系发展面临的难题,提高机场群总体服务质量,增强中小型机场利用率,现有研究主要分为两大类[6-10]:第一类是开展机场群协同运营管理,基于现有机场体系,采用信息共享、协调运营和收益补偿等多种管理方式实现机场群的组织协调和运营维护。通过机场群客运流量预测分析与优化、服务质量调查和发展战略研究等定性分析,结合机场群利益关联性分析、空域和航线调度优化等定量分析方法,能够有效改善机场群总体服务质量和机场利用率;第二类是合理规划机场群体系的空间结构,通过空间规划基本理论和方法,确定机场群空间位置分布,采用新建、改建和废弃等工程方式,在有限资源约束下提高机场可达性,进而实现机场群总体服务质量和承载能力的提高。
截至目前,在交通规划和重大工程管理领域,已有针对机场群体系发展不均衡的相关研究,大部分集中在机场群协同运营管理上,机场群体系空间规划布局的研究鲜见[11-12]。但相比于协同运营管理方式,合理的机场群体系空间规划布局是打破机场群总体服务质量和运营效率瓶颈的基础前提,也是优化机场空域流量及运营管理方式的重要支撑。
为分析机场群体系空间布局对总体服务质量和可达性的影响,本文建立了基于可达性的机场群空间布局分析模型,考虑建设总费用、覆盖范围和机场承载力等多约束条件,并通过MATLAB仿真模拟,探索了不同机场群的空间布局形式并分析其时空可达性,为优化机场群空间结构、提高机场服务质量提供支撑。
1 机场群概念分析
近年来,城市化进程不断推动城市规模扩大,航空运输需求也不断增长。机场作为航空运输的重要枢纽,其新建和改扩建使得机场间距离不断拉近,造成不同等级的机场群越来越多。根据不同区域尺度,机场群通常由一个或多个地区的两个或多个机场组成[11,13]。
机场群在增强区域的航空服务能力和竞争力的同时,也带来了一定的“负效应”[14-17]。一方面,受地缘经济、人口数量和土地利用等影响,空运需求方对时间成本、服务质量和服务频次等差异化需求,单个机场受空间制约又难以全部满足,必须开展群组化协作。另一方面,受机场空域限制、流量瓶颈和票价浮动等多约束影响,机场间的竞争关系在不同层面加剧,使机场群的整体运营效率偏低,难以达到各机场理论上的最大服务能力。因此,要提高机场群覆盖范围和服务质量水平,应在规划之初就开展不同空间布局方案评估和优化,科学合理地规划机场群空间以改善机场间的相互作用关系。
从机场群的主要研究对象上看,机场群主要包含需求方和供给方。其中:需求方指利用机场群从事相关活动的客户,包括客运和货运,供给方为需求方提供服务,通常包括各个航空公司和机场管理者。对客运需求方而言,影响机场选择的因素很多,包括时间成本、服务质量、区域经济、飞机类型、机场设施安全性、燃油价格以及汇率等多个方面。但是,基于旅客出行行为特征的数据表明,到达机场的时间是影响机场选择的主要因素[16, 18]。
对供给方而言,满足价格、服务质量和覆盖范围上的动态多样化需求,促进机场群内相互竞争转化为可持续发展,避免机场运营效率低下,是当前亟待解决的难题。随着需求的不断增长,机场群效率低下会带来的航班延误和拥堵等影响,将产生巨大的经济损失。同时,机场群内的相互依赖,造成的时间和空间限制,反向要求机场群必须耦合协同。而面临这些问题,最为重要的就是解决邻近机场之间相互干扰的问题,应在规划之初就予以统筹[13]。因此,实现机场群空间距离上的合理布局,是机场空域和容量优化的重要基础,也是提高机场群运营效率的前提条件。
对此,综合考虑需求方和供给方两个维度,以实现最大化的机场群服务质量满意度为目标,通过对机场群内不同等级机场容量、经费投入限制和客户选择偏好进行约束,可以建立基于可达性的机场群空间非线性优化模型,并设计相应求解方法以快速实现多区域内机场群空间布局的整体优化分析。
2 基于可达性的机场群空间布局模型
2.1 模型假设
在机场群形成的服务网络中,考虑决策者和投资者总是力图在有限资源投入并满足所有客户需求条件下,会尽可能提高整体服务质量这一要素,结合机场群客运服务特征,本文做出以下假设:
(1)政府决策者本着服务质量总体满意度最大化的原则,会在有限资源范围内尽可能投入资源进行机场群体系建设;
(2)居民出行本着便捷性和随机性的原则,在前往不同机场时其客运流量会依据可达性值按比例进行分配;
(3)机场体系内仅考虑大型枢纽机场、中型骨干机场和小型节点机场3种类型,每种类型的建设费用和最大客运保障能力相同;
(4)在一个时间段内,各位置区域居民空中出行需求不随时间变化,且各位置区域均满足不同类型机场相关建设要求。
2.2 可达性模型
可达性是机场服务的关键因素之一[18-19]。考虑机场最大承载能力、客户与机场距离以及其他因素影响,基于引力模型[20],提出改进的机场群空间可达性引力模型。一方面,相比于中小型机场,大型枢纽机场的承载能力高,设备更新能力强,对居民出行的吸引力更大;另一方面,居民往往偏向距离较近、交通更为便捷的机场。设aij表示在子区域(i,j)内居民的机场群时空可达性,可表示为
∀i∈N1,j∈N2
(1)

对此,机场群体系的时空可达性A可表示为
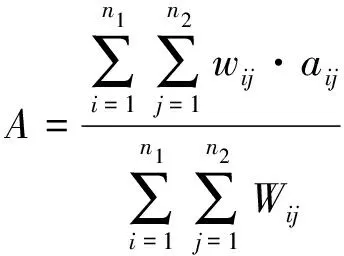
(2)
式中:wij和Wij分别表示子区域(i,j)内居民实际空运流量和需求量。式(2)表明,机场群体系的时空可达性A与居民空运需求总量和实际空运流量相关,且受各区域可达性的影响。
2.3 机场群空间布局模型构建
对于给定的客运需求量Wij∈W,基于可达性的机场群空间布局模型可使用非线性整数规划模型来描述,表示为
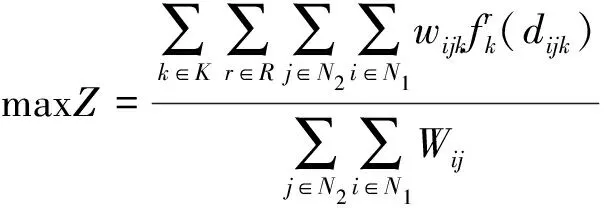
(3)
s.t.
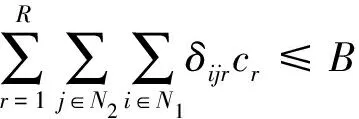
(4)
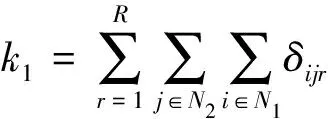
(5)
(6)
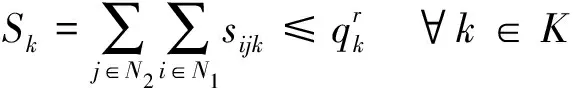
(7)

(8)

(9)
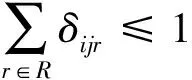
(10)
wij≤Wij
(11)
wij≥0 ∀i∈N1,j∈N2
(12)
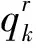
式(4~7)分别表示机场群体系建设经费投入总量、机场建设总数量、各需求区域最低服务水平以及各机场最大客运流量的约束条件;式(8,9)表示出行需求和机场客运流量的守恒关系;式(10)表示各子区域最多只能修建一个机场;式(11,12)表示在整个机场群体系中,各区域实际客运流量应小于或等于需求量,且具有非负性。
3.设置的问题要有灵活性。同一教学方法可以解决不同的教学内容,不同的教学方法也可以解决相同的教学内容;同一教学方法面对不同的教学对象会产生不同的教学效果,不同的教学方法面对相同的教学对象也会产生不同的教学效果。因此,教学策略的运用要随着问题、目标、内容和教学对象的不同而改变。
3 模型求解与算法设计
机场群空间布局模型具有非线性特征,属于整数规划问题,其求解方法通常分为解析方法和启发式算法[21]。其中,解析方法一般将非线性问题等价或者松弛转化为线性规划问题进行求解,但转化难度高且计算效率低,较适合小型网络。而相较于解析方法,启发式算法不直接依赖模型的数学性质,可以快速地获得近似全局最优解。因此,本文基于粒子群算法来求解基于可达性的机场群空间布局模型。
粒子群算法是一种基于群体智能的优化方法,具有全局优化能力,在系统设计、目标优化、生物工程、疾病治疗等领域得到了广泛的应用[22-24]。为了解决复杂环境下的优化问题,粒子群通常通过粒子间的协作和信息共享来调整每个粒子的运动。在机场群空间布局模型求解上,通常将每个粒子视为没有质量或大小的点来代表一个可行解,为自变量δijr的集合,并使用目标函数值Z的大小来评估粒子是否为较优可行解。以n1和n2取值分别为4和5为例,区域内共包含20个子区域,其中有6个子区域存在空运需求,其最优化过程如图1所示。
其中,第i个粒子可表示为Gi,含有n3个粒子的群集合可表示为G=(G1,G2,…,Gn3)。则在t时刻,Gi的位置、速度和对应的服务质量总体满意度值可分别表示为Pi(t)=(δ111i(t),δ112i(t),δ113i(t),δ121i(t),δ122i(t),δ123i(t),…,δn1n21i(t),δn1n22i(t),δn1n23i(t))T,Vi(t)=(v111i(t),v112i(t),v113i(t),v121i(t),v122i(t),v123i(t),…,vn1n21i(t),vn1n22i(t),vn1n23i(t))T和Zi(t)。在优化搜索和趋向移动过程中,一旦全体发现较优解,其他粒子将利用PSO算法调整速度方向和大小,趋近较优解粒子所在的位置。
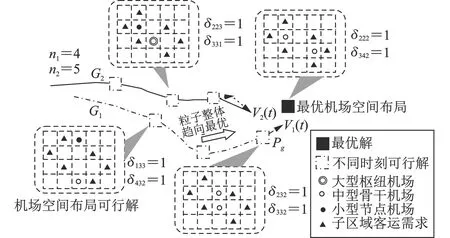
图1 利用粒子群算法寻找机场群最优空间布局过程示意图
以求解机场群体系的总体满意度为例,在t时刻,粒子Gi对应目标函数历史极值位置为Ppi,整个群体历史极值位置为Pg,则从时间t到t+Δt,由个体粒子历史极值和全局极值的更新,粒子Gi的速度和位置也将更新,表示如下
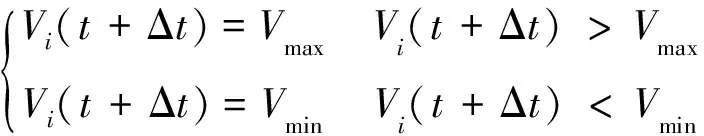
(13)
Pi(t+Δt)=Pi(t)+Vi(t+Δt)Δt
(14)
式中:φ表示惯性权重,权衡粒子Gi按照上一时刻速度惯性移动的程度;b1和b2分别表示粒子Gi从个体和群体运动中吸取经验的学习因子;两个相互独立的随机数λ1和λ2分别表示粒子随个体和群体移动的随机性,其取值范围在0到1之间;Vmax和Vmin分别表示粒子Gi移动的最大速度和最小速度。
基于可达性的机场群空间布局模型的求解流程如图2所示。本文采用MATLAB软件进行仿真,其主要步骤如下:
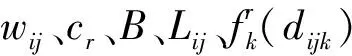
步骤2PSO算法基本参数设置与状态初始化。输入n3、φ、b1、b2、λ1、λ2、Vmax、Vmin等参数并设置最大迭代次数tmax,依据式(4~11),随机给出t=0时刻符合约束条件的粒子初始位置和初始速度,并根据式(3)计算此时各粒子对应的服务质量总体满意度值;
步骤3粒子个体与群体极值计算与迭代更新。依据式(12,13),更新粒子和群体历史极值后,再次计算各粒子位置和速度,以及对应的服务质量总体满意度值;
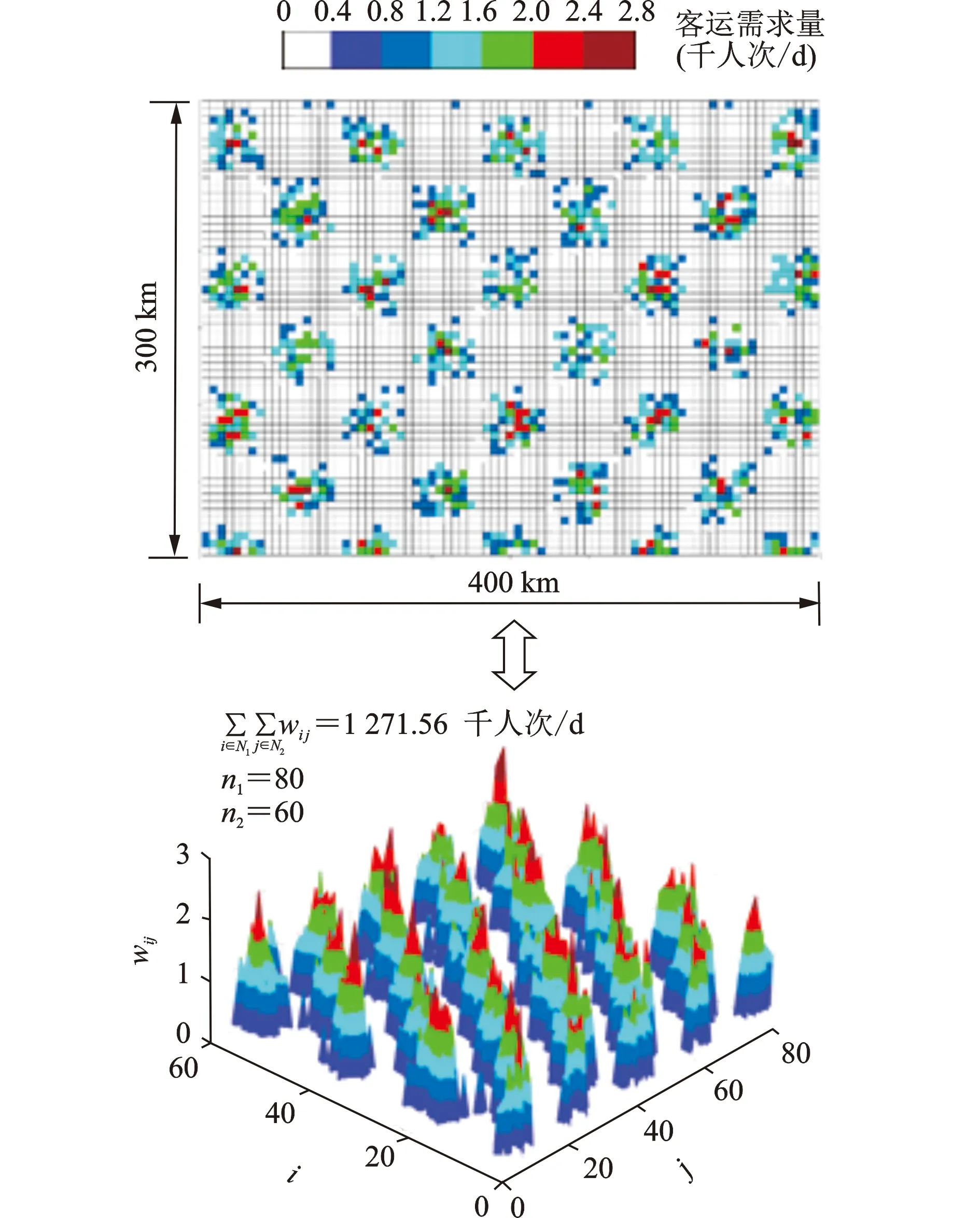
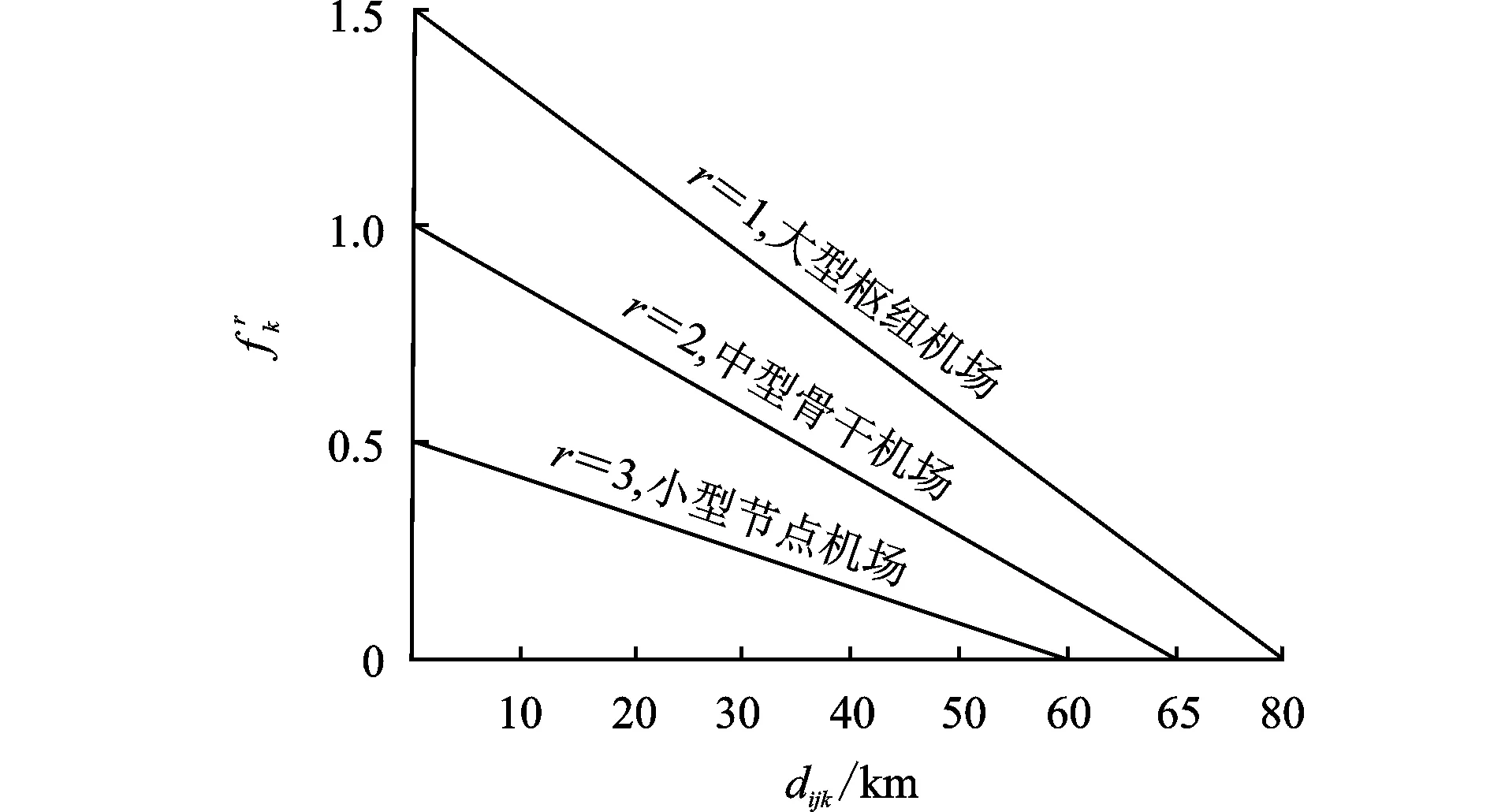
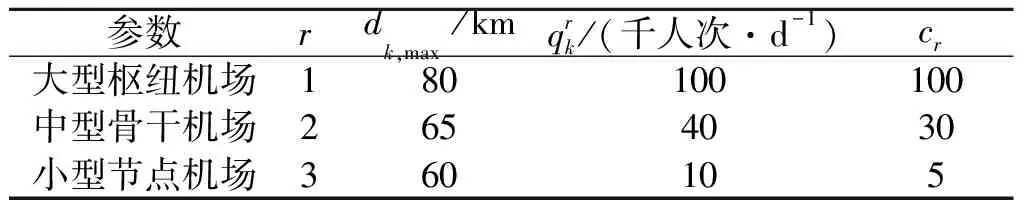
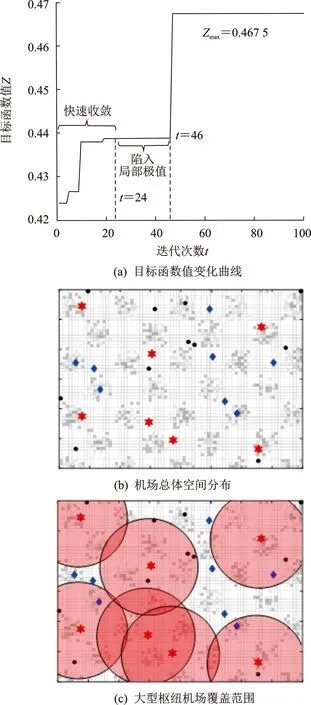
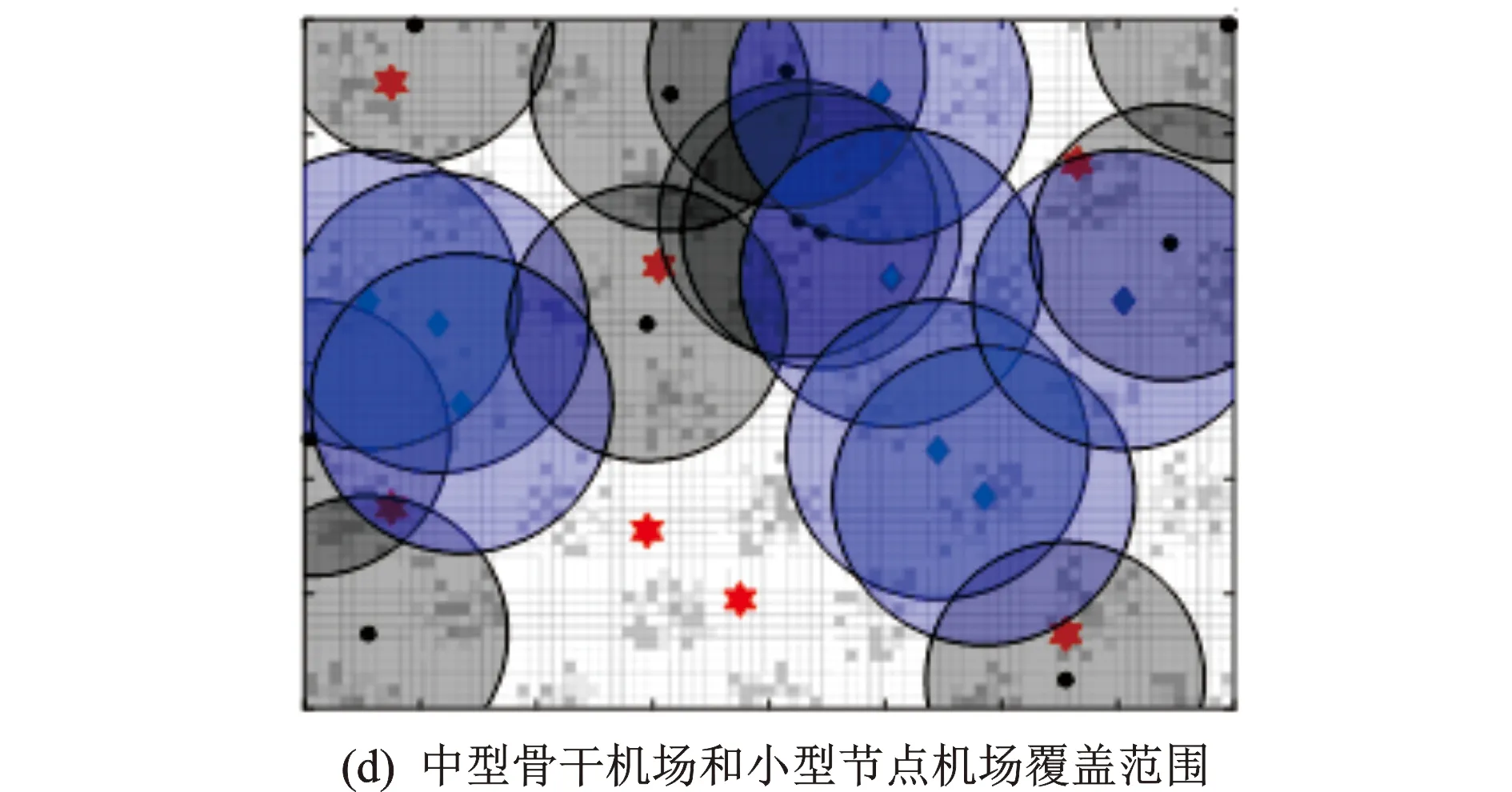
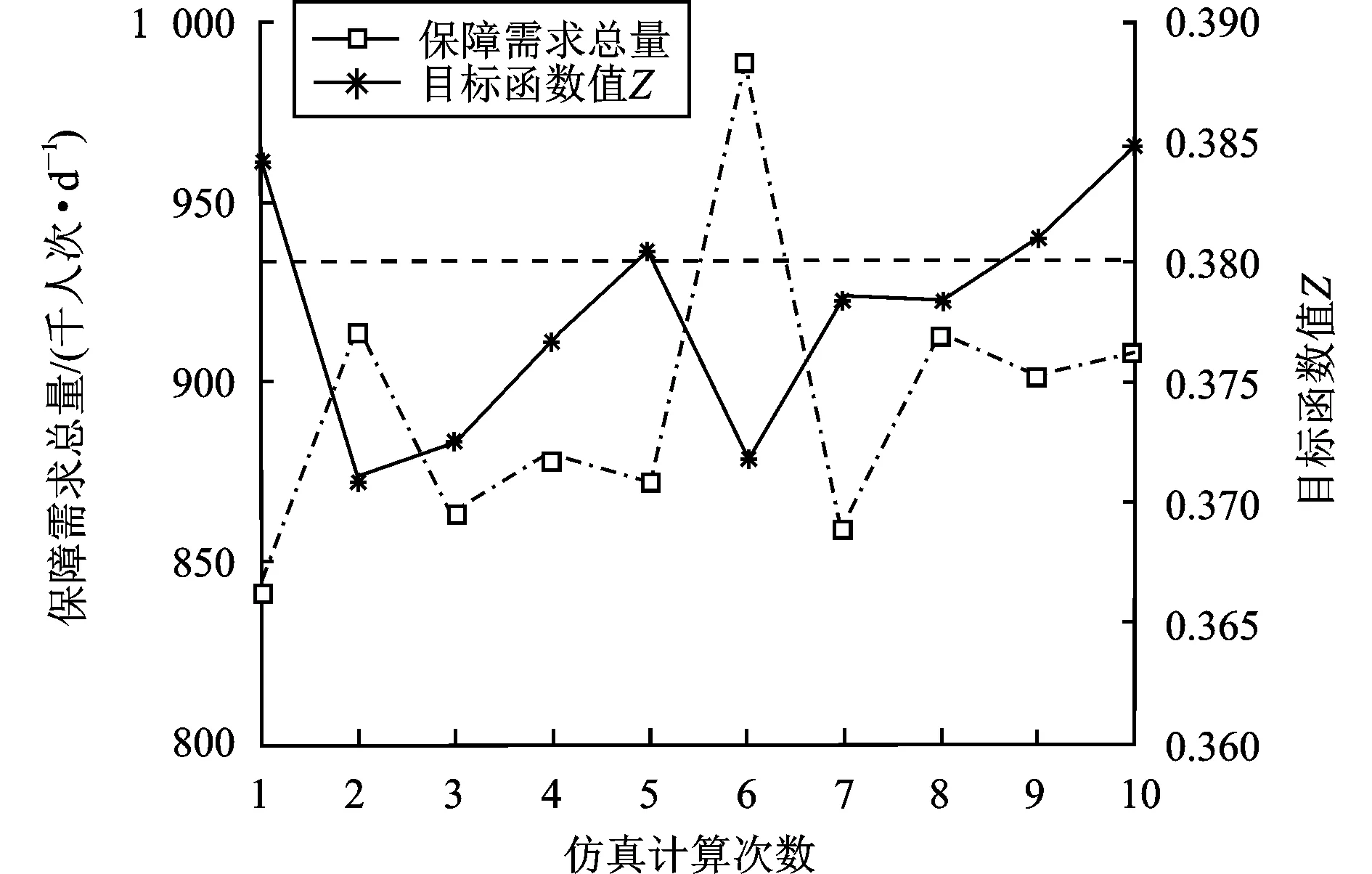
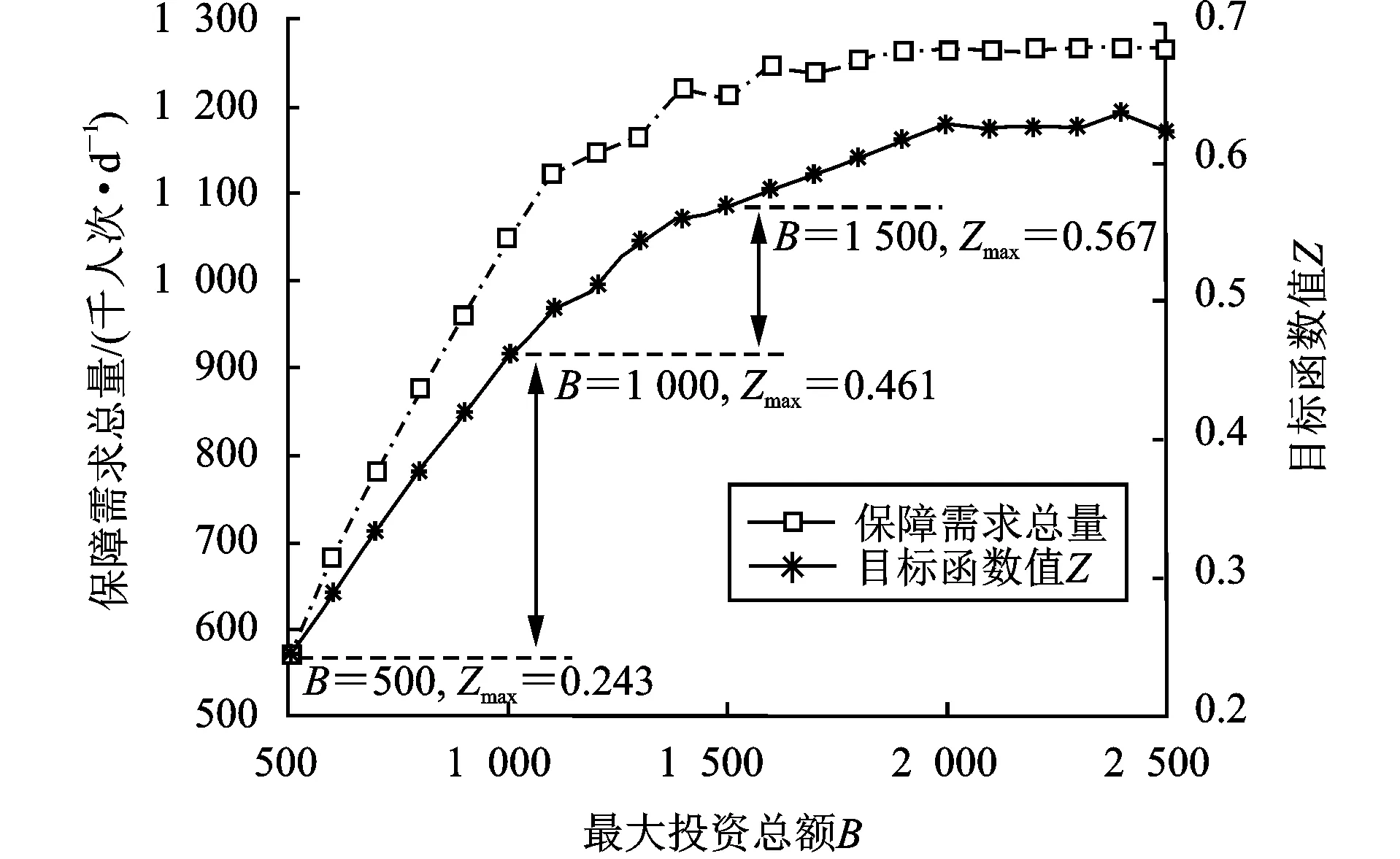
步骤4循环判断与结果输出。若t 图2 基于可达性的机场群空间布局模型求解流程图 本文选取目标区域大小为400 km×300 km进行算例分析,n1和n2分别取值为80和60,将目标区域共划分为4 800个子区域,每个子区域尺寸为5 km×5 km。考虑空运需求随城市布局的聚集分布特征以及地域区别,为随机生成需求分布,本文使用的需求函数为 (15) 式中:μ1和μ2分别为相互独立的随机数,取值为0到1之间,在每次随机生成子区域需求量wij时,其取值是随机变化的。图3表示目标区域内随机生成的空运需求对应的二、三维空间分布,在本案例中,空运需求总量为1 271.56 千人次/d。 图3 目标区域空运需求二、三维示意图 图4 不同类型机场服务质量随机场与子区域距离变化示意图 表1 不同类型机场的参数设置 表2 案例其他相关参数设置 案例仿真计算结果如图5所示。其中:图5(a)表示仿真计算过程中目标函数值随迭代次数的变化曲线;图5(b)表示机场总体空间分布计算结果;图5(c,d)分别表示总体空间分布对应各类型机场最大的覆盖范围。由图5(a)可知,当t=24时,目标函数值快速收敛为0.438 9,并一直陷入局部极值,直到t=46时,目标函数值达到最优,总体满意度Zmax取值为0.467 5。 图5 案例计算结果 案例计算仿真结果表明,利用PSO算法,可以快速搜索到较优可行解,并且随迭代次数的增加,目标函数值不断地优化更新。 由图5(b)可知,为满足空运需求,该地区需新建26个机场,费用占总投资99.5%,涵盖7个大型枢纽机场、8个中型骨干机场和11个小型节点机场。在本案例中,大型枢纽机场、中型骨干机场和小型节点机场的保障需求总量分别为687 417、302 623和90 538 人次/d,保障的比例分别为63.61%、28.01%和8.38%。此外,受需求分布影响,新建机场总体空间分布较为均匀,且大型枢纽机场分布较分散,其主要原因是在有限投资下,空运需求分布的广泛性导致新建机场应尽可能考虑未被覆盖地区。 由图5(c,d)可知,大型枢纽机场覆盖范围大,一般难以满足覆盖范围内所有区域的空运需求,需要中型骨干机场和小型节点机场进行补充。此外,各类型机场一般远离各区域需求量较大位置,其主要原因是需求分布具有多中心聚集性,导致机场建设选址上需考虑覆盖更多的出行需求。 不同的机场群建设投资总额会影响各类型机场数量及比例,进而形成不同的机场群空间布局。为了分析不同的投资总额变化对机场群分布以及总体满意度Zmax的影响,以合理确定最大投资总额,本文设置21个案例进行仿真实验,其最大投资总额B的取值符合等差分布,最小值为500,公差为100。考虑粒子群算法具有偶然性和随机性,将每个案例进行10次仿真计算。其中,以B=800为例,其10次仿真计算结果如图6所示。 从图6可以看出,10次仿真计算得到的目标函数值各有不同,呈波动特征,但总体上靠近0.38,表明尽管算法具有偶然性和随机性,但在一定迭代次数条件下可有效搜索到较优可行解。此外,在同一案例下,机场群体系的保障需求总量与目标函数总体满意度的值并不存在线性关系,保障需求总量增加,目标函数值反而可能会下降,主要原因是总体满意度不仅与保障需求相关,且与各子区域的距离相关。 图6 B=800时案例的仿真计算结果 为消除算法的偶然性和随机性,分析最大投资总额B对保障需求总量和总体满意度的影响,将每个案例进行10次仿真计算后取平均值,如图7所示。从图7可以看出,在整体上,机场群体系保障需求总量和目标函数值随着最大投资总额增加而增加,且上升速率逐渐变缓并趋于0。主要原因是随着最大投资总额增加,机场群体系规模逐渐扩大,已经能够满足当前各子区域的空运需求量,再新建其他机场容易造成闲置现象。 图7 最大投资总额B变化对保障需求总量和目标函数值的影响 机场群体系空间规划布局理论研究是机场群体系建设发展的基础支撑,也是优化机场体系运营管理方式的重要依据。本文建立基于可达性的机场群空间布局分析模型,提出基于粒子群算法的快速求解方法,通过MATLAB仿真模拟,分析了有限资源约束下机场群体系空间布局对总体服务质量的影响,并探讨了资源变动条件下机场群体系总体满意度的变化趋势。案例研究结果表明: (1)利用粒子群算法求解基于可达性的机场群空间布局模型,可以快速得到满足模型的可行解,并通过不断迭代来优化机场群空间分布,提高机场群服务的总体满意度; (2)在一定投资总额约束下,机场群总体分布均匀,大型枢纽机场、中型骨干机场和小型节点机场互为补充,且大型枢纽机场、中型骨干机场和小型节点机场承担的空运需求依次递减; (3)在一定投资总额下,机场群体系的保障需求总量与总体满意度并不存在线性关系。同时,机场群体系保障需求总量和目标函数值随着最大投资总额增加而增加,且上升速率逐渐变缓。
4 算例与仿真计算
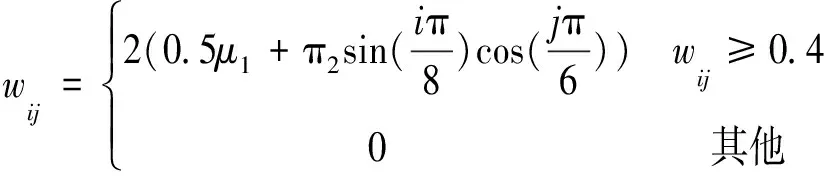
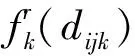

5 结果分析与讨论
5.1 案例计算结果分析
5.2 最大投资总额影响分析
6 结论
- 陆军工程大学学报的其它文章
- 一种战时航空弹药需求预测方法
- 装备维修器材仓库选址鲁棒优化模型

