多柔性附件卫星热致振动特性研究

陈夜 王开浚 沈海军 张雷霆 彭海阔

(上海卫星工程研究所，上海 201109)

由于质量轻、收纳比高的优势，大柔性可展开结构已广泛应用于各类卫星[1-2]，以实现高分辨率对地观测、大容量通信等任务目标。大尺寸伸展臂、蜂窝板以及薄膜结构是卫星上常见的柔性附件，对温度变化、微振动等环境因素敏感度高，容易发生在轨振动。绝大多数卫星在轨运行时会周期性地出入地影区，期间卫星外热流发生突变，导致星上温度的迅速变化，诱发柔性附件乃至整星的振动，即热致振动，影响卫星的姿态精度与稳定性，为有效载荷的工作性能带来不利因素。

公开文献可查由星上大柔性附件引发的航天器热致振动事故，有地球物理观测卫星-4(OGO-IV)[3]、哈勃太空望远镜(HST)[4]、尤里塞斯(Ulysses)航天器[5]等。其中以哈勃太空望远镜最为典型，周期性的瞬间温差变化使太阳电池阵反复热胀冷缩，激起了太阳电池阵的共振，引发指向控制系统的扰动，导致传回的图像模糊失效。

对航天器热致振动机理的研究始于20世纪50年代，Boley首次提出了热致振动的概念[6]，并定义了Boley参数[7]用来判断结构是否会发生热致振动。哈勃望远镜的热致振动引起了很多航天学者的关注，文献[8]利用梁模型分析了望远镜热致振动的机理，并得出了弯曲振动稳定性的判据。进入21世纪，随着有限元方法的发展与计算机能力的提升，多数学者采用数值方法[9]进行热致动力学分析，文献[10-11]提出了傅里叶温度单元，可高效地用于瞬态热-结构动力学的计算。文献[12]对空间桁架、文献[13]对环形桁架天线等结构的热致振动特性进行了仿真分析，为结构优化设计提出了方向。

上述研究深入分析了热致振动的产生机理，实现了典型空间柔性附件的热致振动分析计算。对于搭载多柔性附件的卫星，柔性附件的振动相互牵连，单一附件的振动分析已不能反映真实的振动特性，本文通过热致动力学建模，对整星级的热致振动进行分析。

1 热致振动有限元建模

1.1 热弹性力学基本方程

温度变化引起的力学问题属于热弹性力学范围，故在线弹性范围内的连续性假设、均匀性假设、各向同性假设、完全弹性假设、小变形假设依然成立，平衡方程、几何方程与一般弹性力学的方程完全相同[14]，但从物理学角度，由于膨胀或冷缩仅产生线应变，剪切应变为零，故其物理基本方程为

σ=Dε-Dε0

(1)

式中：σ是单元应力列向量；ε是单元应变列向量；D为弹性常数矩阵；ε0为单元温度应变量。对各向同性材料，其表达式为

(2)

式中：α为线性膨胀系数；ΔT为温度变化量。

1.2 热弹性单元动力学方程

随着计算机技术的发展，有限元方法已广泛应用于航天领域的动力学分析，将结构离散为弹性单元，基于单元构建整星的动力学方程。

根据有限元理论，单元内的位移场u、应变场ε可由出口节点位移ue表示，即

u=Nue，ε=Bue

(3)

式中：N为型函数；B为应变-位移转换矩阵；e为单元编号。

假设单元除承受体积力FV、表面力FS、集中载荷P的作用外，还发生了热应变ε0，则根据虚功原理可推导出热弹性单元的动力学微分方程为

(4)

式中：Me、Ce、Ke、re分别为单元质量阵、阻尼阵、刚度阵、节点力列阵，其表达式如下。

(5)

式中：ρ为单元材料密度；c为阻尼系数。

相比于恒温条件下的单元动力学微分方程，式(4)增加了热载荷项rTe，rTe通过单元体积内积分得到

(6)

1.3 整星级热致动力学方程

式(3)中的动力学微分方程是在单元局部坐标系下描述，需要将各单元的动力学方程统一到整星坐标系下。用下标a、b分别表示整星坐标系和局部坐标系，假设局部系{eb}到整星系{ea}的转换矩阵为T，热弹性单元的出口节点位移在整星系下表示为

(7)

则整星坐标系下的单元矩阵为

(8)

(9)

整星级热致动力学微分方程可表示为

(10)

式中：x为整星的n×1维广义位移列阵；M、C、K分别为整星的n×n维质量矩阵、阻尼矩阵、刚度矩阵；r、rT分别为整星的外激励与热载荷矩阵。

热致振动分析的特殊之处在于，需要根据外热流条件或温度条件计算热载荷矩阵rT，对于时域上无法用解析式描述的温度场，只能用数值方法求解式(7)，且数值积分的时间步长要足够小，以充分描述温度的变化。ABAQUS软件的隐式动力学模块[15]能够将动态、离散的温度载荷条件映射到有限元模型，将时间历程离散为微小的时间步，通过数值积分，实现热致动力学方程的求解。

1.4 振动响应的解耦分析

对于多柔体卫星，温度变化可以同时引发多个柔性附件的振动，振动通过卫星本体的传递，相互耦合叠加，表现出更加复杂时域特性。因此，除得到卫星的热致振动响应外，还希望辨识振动的源头，为振动抑制方案的制定提供方向。

依据模态叠加与模态截断[16]原理，柔性结构的振动主要由低阶模态分量组成，即位移x可表示为m个正交主振型的线性组合

(11)

式中：ξi为模态坐标；φi为第i阶模态振型。

通过快速傅里叶变换将位移的时域响应x(t)变换到频域x(w)，则有

(12)

模态坐标ξi(w)在其对应的固有频率wi处存在明显的峰值，所以x(w)在固有频率w1，w2，…，wm附近会出现大小不等的峰值，据此可识别热致振动的频率组成。而各阶固有频率一般对应一个主振附件，由此可以辨别振动的主要源头，实现振动的解耦分析。

2 应用实例

2.1 卫星特点

以某遥感卫星为例开展分析，卫星上搭载了太阳翼、伸展臂、抛物面天线等多个大柔性附件，如图1所示。发射状态下，柔性附件以折叠方式收拢，入轨后展开，伸展臂、抛物面天线的长度均达到10 m以上。柔性附件降低了整星在轨状态的固有频率，使得卫星具有复杂的动力学特性。

图1 卫星在轨展开状态

高精度平面阵天线是卫星搭载的主要载荷之一，位置稳定度是保证该天线性能的关键因素。天线悬挂于柔性伸展臂的末端，伸展臂与卫星本体间采用柔性连接的方式，容易在温度环境扰动下发生振动。而柔性结构的振动衰减缓慢，持续扰动将影响天线的正常工作，因此在卫星设计与论证中必须开展相关的分析与评价。

通过初步动力学分析，卫星本体的固有频率在10 Hz以上，远大于柔性附件，卫星可视为一个中心刚体与多个柔性附件的组合结构。卫星在轨状态下，某个柔性附件发生振动后，扰动力将传递给卫星本体。由于角动量守恒，卫星本体与其他附件也将发生牵连振动。因此，柔性附件上的热致振动由以下两种因素叠加而来：

(1)柔性附件上温度突变引发的附件自身振动；

(2)其他附件热致振动经卫星本体传递来的扰动。

2.2 动态温度场

通过建立卫星热分析有限元模型，综合考虑轨道环境热辐射、卫星表面辐射、热载荷等因素，得到一个轨道周期(约6100 s)内卫星在各个时刻的温度场。选取均匀分布在太阳翼、抛物面天线、伸展臂上的节点，输出温度变化曲线如图2所示。

图2 一个轨道周期的温度变化曲线

第2400 s与第3400 s是卫星进、出地影时刻，太阳翼、抛物面天线的温度在这个时间段内变化尤为剧烈。为突出进、出地影期间温度变化的影响，截取2400～4000 s时间段的温度场作为后续分析的热载荷条件。

2.3 卫星在轨模态

模态分析是结构动力学分析的基础，也是振动响应解耦分析的主要依据。因此，在建立卫星的结构分析有限元模型后，首先开展模态分析，边界条件为自由边界，模拟卫星在轨运行状态。过滤掉6阶刚体模态，卫星的弹性模态如表1所示。

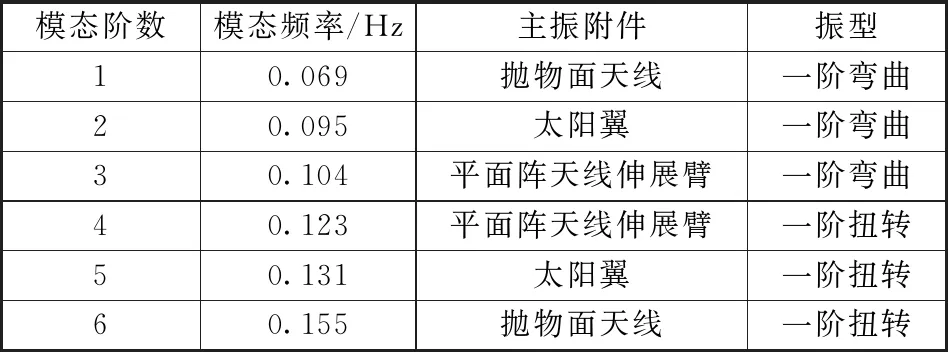
表1 卫星在轨模态

柔性附件的存在使得卫星在低频段模态密集，卫星一阶固有频率为0.069 Hz。

2.4 热致振动分析

基于ABAQUS软件的隐式动力学模块开展时域动力学分析。分析时间范围为0～3000 s，其中第0～1600 s加载进、出地影时间段内(图2中2400～4000 s)的温度场，第1600～3000 s温度场保持恒定，研究热致振动的产生以及衰减规律。

分析发现柔性附件角点上的变形与振动最为明显，以角点上的位移表征附件的振动特性，得到太阳翼、抛物面天线、平面阵天线的位移时域响应曲线如图3所示。

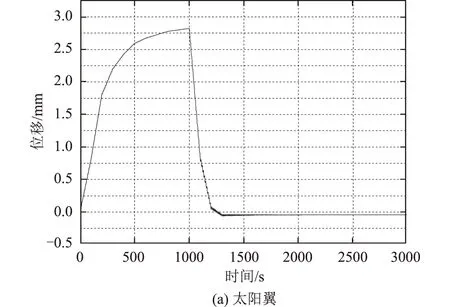
图3 柔性附件位移时域响应曲线

位移时域曲线呈现准静态分量占主导的特征。从振动量级上，热致振动幅值明显小于准静态变形量；从振动时间上，热致振动随着准静态变形的突变而产生，并随着准静态变形的稳定而衰减。在图3中，1000 s后的热致振动效应较为明显，是由于第1000 s为卫星出地影时刻，星上温度在此刻由降转升。自1300 s开始，由于温度变化趋缓，柔性附件的准静态变形逐渐保持稳态，振动缓慢衰减。截取各附件的位移稳态衰减曲线，如图4所示。

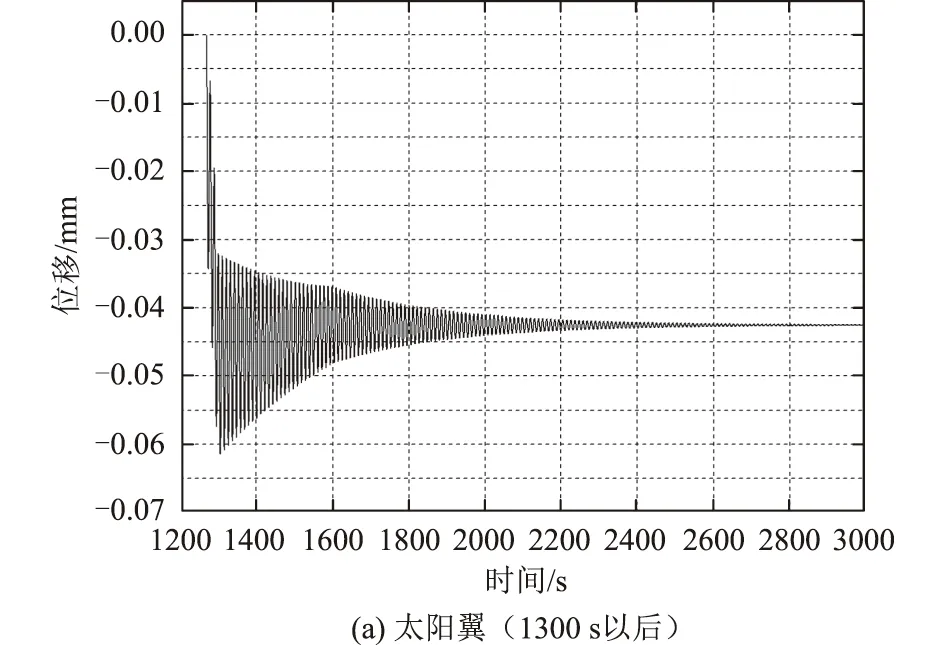
图4 稳态振动曲线

由图4可见，太阳翼、抛物面天线的振动曲线接近正弦衰减振动，说明振动的频率组成较为单一，而平面阵天线的振动曲线比较复杂，是多种频率振动叠加的结果。

从振幅角度，太阳翼与抛物面天线的最大振幅约为30 μm，平面阵天线振幅小一个量级，约为3 μm。在时间历程上，当准静态位移达到稳态后，各柔性附件的振动幅值在800 s后均衰减了90%以上。

2.5 振动源辨识

为辨识热致振动的主要频率组成，首先对图4的振动曲线进行快速傅里叶变换。考虑到柔性结构的固有频率普遍在1 Hz以内，快速傅里叶变换的采样频率定为2.5 Hz，变换后的有效频域范围为0～1.25 Hz。热致振动的频域曲线如图5所示。

依据图5各柔性附件振动的频域曲线在0.069 Hz处均存在明显的峰值，即存在0.069 Hz的振动分量，对应抛物面天线的一阶弯曲模态。可见抛物面天线的弯曲振动引起了整星的牵连振动，是卫星热致振动的主要源头。

图5 热致振动频域曲线

对于有高稳定性要求的平面阵天线，其振动频域曲线还存在0.104 Hz、0.123 Hz两处峰值，对应伸展臂的弯曲与扭转模态。因此，若需进一步提高平面阵天线的稳定性，一方面要通过温度控制、提升固有频率等手段降低伸展臂的热致振动效应，另一方面还应通过隔振措施减弱抛物面天线振动的传递。

3 结论

通过整星级的热致动力学建模，并结合应用实例，得出以下结论：

(1)对于搭载有柔性附件的卫星，尤其在附件固有频率小于0.2 Hz的情况下，卫星的设计论证阶段应考虑热致振动效应的影响；

(2)对于搭载多个柔性附件的卫星，分析热致振动对关键载荷的影响时，应考虑振动的传递与叠加效应，并通过解耦分析识别主振附件；

(3)相关研究内容可为多柔性附件卫星的振动抑制设计提供方向，提高卫星在轨运行期间的稳定性。