地铁深基坑施工安全评估FDEMATEL-TOPSIS模型及应用

刘毅，孙庆文，刘贵香，蒙国往，李想*，吴波

(1.济南轨道交通集团有限公司，济南 250101；2.中铁北京工程局集团有限公司，北京 100089；3.广西大学土木建筑工程学院，南宁 530004)

随着工程技术的发展，地下空间的开发在不断推进，尤其是地铁的建设过程中出现越来越多的深大基坑，且同时伴随着复杂的地质条件和周边环境条件，给基坑施工带来巨大风险[1]。因此为保障工程项目顺利进行，防范意外事故发生，对地铁车站深基坑施工进行安全风险分析具有重要作用。

基坑工程施工环境复杂，一旦发生事故将对自身和周围环境造成较大损失。在以往的研究中侧重于概率风险分析，并发展了许多评估方法，如贝叶斯网络[2]、事故树法[3]、层次分析法[4]、模糊综合评判法[5]等。Zhou等[6]提出一种基于贝叶斯网络的风险分析模型，根据施工现场数据，实现了整个施工过程的动态分析。陈绍清等[7]将事故树与层次分析法结合对基坑坍塌事故进行定性和定量分析，确定了其主要致灾因素。朱琦等[8]将多目标层次分析与模糊综合评判法结合，提出了合理、可靠的深基坑支护方案。概率方法的应用需要有效可靠的数据，然而基坑工程中风险具有高度不确定性和模糊性，上述方法在应用中难以得到满意的结果。为了更科学地处理基坑项目风险评估中不确定信息，模糊数学理论被广泛应用。针对地铁车站基坑工程施工过程中的不确定性和模糊性，Wang等[9]将模糊综合评判法与贝叶斯网络结合，从风险概率、风险损失和风险可控性3个方面对风险进行分析。Wei等[10]提出了一种基于模糊证据理论的风险评估方法，采用模糊数描述概率与后果乘积，证据理论推算总体风险水平，结果证明该方法能有效评价深基坑总体风险水平，较传统方法更加合理。Shen等[11]利用层次分析法和模糊集理论对某地铁车站基坑进行风险评估，确定其关键风险因素以及风险等级。Yan等[12]结合模糊集和物元理论，提出了一种模糊物元风险评价模型，解决评估过程中模糊不相容问题，客观反映风险指标的影响。模糊数学理论的引入促进了深基坑风险的研究，基坑工程施工过程中风险因素众多，风险因素的重要性可通过赋予不同的权重来描述。然而这些风险因素通常是相互关联的，上述研究在确定其权重时认为它们是相互独立的。决策与试验评价实验室(decision-making trial and evaluation laboratory，DEMATEL)方法能够分析复杂系统中各因素之间的相互依赖性，已经在控制决策、风险分析等方面得到广泛的应用。成连华等[13]构建了基于AHP-DEMATEL方法的模型，确定了建筑施工项目中的关键风险指标。岳仁田等[14]运用DEMATEL-Choquet模型对航班运行风险进行了评价，确定了影响航班运行的关系风险因素及其影响程度。目前DEMATEL方法在基坑工程中应用较少，根据其能分析复杂系统中各因素之间联系的特点，可以将其运用到基坑工程中来。逼近理想排序方法(technique for order preference by similarity to an ideal solution，TOPSIS)能判断多个对象之间的优劣关系[15]，给基坑各风险事件排出重要性等级，有助于基坑风险决策。吴波等[16]采用TOPSIS法研究隧道施工的时空效应，得到了影响隧道施工时空效应的最优施工方案。李新平等[17]结合组合赋权与TOPSIS法对隧道突涌水风险进行了评价，得到了隧道突涌水风险等级以及危险最大的洞段。基于以上原因，本文将模糊数学理论、DEMATEL法与TOPSIS法结合，建立深基坑施工风险评估模型。

基于此，现提出一种基于模糊决策与试验评价实验室(fuzzy decision-making trial and evaluation laboratory，FDEMATEL)方法和TOPSIS方法的风险评估模型。首先根据基坑中各风险因素相互关联且具有较大模糊性特点，将模糊数学理论与DEMATEL方法结合确定各风险因素的权重。然后采用TOPSIS法对各风险因素进行重要性排序，确定最关键的风险因素，综合各因素的权重值和贴近度得到基坑施工风险等级。以济南轨道交通R2线烈士陵园站为实例进行应用，得到较为可靠的结果，以期为类似工程提供参考依据。

1 基本理论

1.1 模糊DEMATEL理论

DEMATEL是一种系统化分析决策方法，通过描述各因素之间的影响关系进行建模，然后根据矩阵理论计算各个因素的原因度与中心度，从而得到各元素间的因果关系和每个因素自身在系统中的重要程度[18]。模糊DEMATEL是在传统的DEMATEL法上结合模糊集理论而来的，相较于传统DEMATEL它能更好地处理不确定信息，适用于数据较少和较模糊的情况[19]。梯形和三角形隶属函数应计算简便在工程中得到广泛使用，为了便于计算，本文采用三角模糊数来描述专家语言[20]，按照如表1所示的规则将专家语言转换为模糊数，采用模糊DEMATEL确定风险因素的权重具体步骤如下。

步骤1收集专家对各因素间相互影响关系的术语判断，如非常高、高、中等、低、非常低、无等来建立直接影响矩阵A,将A用表1规则转换为模糊直接影响矩阵K。

表1 语言变量和模糊数

(1)

(2)

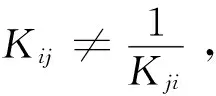
步骤2将模糊直接影响矩阵K按式(3)和式(4)进行去模糊化得到矩阵O。

(3)

(4)

步骤3再将矩阵O按式(5)和式(6)进行归一化得到归一化矩阵Z。

(5)

(6)

步骤4通过式(7)计算模糊综合关联矩阵T。

T=Z+Z2+…+Zm=Z(1-Z)-1

(7)

步骤5使用式(8)和式(9)计算矩阵T中每行元素的和fi，每列元素的和ei。fi为影响程度，ei为被影响程度。将影响程度和被影响程度相加得到中心度Ei，得到的值越高说明该因素越重要，两者相减得到原因度Fi，值大于零的话说明因素i对其他因素有影响作用，如果小于零则说明因素i被其他因素影响。

(8)

(9)

步骤6得到影响度和被影响度之后，由式(10)得到关系矩阵D,其对角线元素定义为影响度向量d，权重Wi通过式(11)求得。

(10)

(11)

1.2 TOPSIS理论

TOPSIS法是一种多目标决策分析方法，计算有限个评价对象与最优目标之间的贴近度来进行排序，根据距离的大小来评价目标的优劣[21]。贴近度越靠近1则评价对象越接近最优水平，贴近度越靠近0则该评价对象越接近最差水平。通过判断风险指标与最优目标间的贴近度来区分风险的优先级，以此依据来帮助风险管理，本文对每个风险指标从发生概率和造成的损失两方面来评价。其具体步骤如下。

步骤1建立初始评判矩阵。

初始评判矩阵A由m个待评价方案和n个评价指标组成。

(12)

式(12)中：aij为第i个方案的第j个指标的分值；i=1,2,…,m，j=1,2,…,n。

步骤2计算加权评判矩阵。

将初始评判矩阵与由模糊DEMATEL得来的权重W相乘得到加权评判矩阵B。

B=(bij)m×n=AW，i=1,2,…,m;

j=1,2,…,n

(13)

式(13)中：bij为第i个方案的第j个指标的加权分值；i属于1～m，j属于1～n。

步骤3求解正负理想解。

正理想解B+=(maxbi1,maxbi2,…,maxbin)，即矩阵B中每列的最大值。

负理想解B-=(minbi1,minbi2,…,minbin)，即矩阵B中每列的最小值。

(14)

(15)

步骤5计算各备选方案与正理想解的贴近度，即

(16)

1.3 评估体系及流程

模糊DEMATEL理论既考虑了基坑施工过程中风险的不确定性、模糊性，又考虑了各风险指标间的相互关系。TOPSIS能够对各风险指标进行一个轻重缓急的排序，将两者结合的评估模型有助于了解深基坑工程施工过程中有哪些危害，其综合风险有多大，哪些危害是应优先处理的，评估流程图如图1所示，其具体操作流程如下。

图1 评估流程图

(1)构建模糊直接影响矩阵K和初始评判矩阵A。

(2)将模糊直接影响矩阵经去模糊化、归一化等转换得到综合关联矩阵T。

(3)求解影响度、被影响度、中心度和原因度，根据式(11)求解权重。将所求权重与初始评判矩阵结合得到加权评判矩阵。

(4)求解正负理想解以及各指标到正负理想解之间的欧式距离。

(5)计算贴近度，得到各风险指标的重要性排序。

(6)将风险因素权重与其贴近度结合计算基坑整体风险等级。

将风险水平分为4个等级，低风险(Ⅰ)、中等风险(Ⅱ)、高风险(Ⅲ)、较高风险(Ⅳ)，其相应的基坑总体风险值R的描述如表2所示。

表2 风险等级与接收准则

采用式(17)将已经得到的各指标权重值乘以贴近度进行综合，得到基坑总体风险值R和风险等级。

(17)

式(17)中：Wi为第i个风险指标的权重；Ei为第i个风险指标的贴近度。

2 案例研究

2.1 工程概况

烈士陵园站为济南轨道交通R2号线的第17座车站，为地下两层车站，车站基坑开挖属深基坑开挖，车站底板基本位于地下水水位以下，确保车站基坑安全是本工程的重点之一。车站采用明挖顺筑法施工，结构形式为混凝土箱型，站台宽14 m，有效站台长140 m，基坑主体结构采用φ1 000@1 200钻孔灌注桩，沿深度方向设置钢支撑，基坑围护结构和地层分布如图2所示。车站周围有新建泵站、员工宿舍、正在拆迁的村庄等建筑。车站范围内分布有雨污合流管、热水管、弱电、天然气、输油管等管线。烈士陵园站南侧为石灰岩分布区，工程区域地下水水位较高，钻孔揭露地下水类型为第四系松散层孔隙潜水和碳酸盐岩溶裂隙水，岩浆岩裂隙水和碳酸盐岩溶裂隙水微具承压性，施工时可能会发生地下水突涌情况，基坑开挖影响范围内地层主要为黏土层、碎石层、残积土、闪长岩。黏土层遇水易软化、崩解。

图2 围护结构设计剖面图

2.2 风险指标体系建立

以现场勘测资料和城市轨道交通地下工程建设风险管理规范为基础采用工作分解结构(work breakdown structure，WBS)将基坑工程风险按工序分解为基坑围护与支撑(U1)、基坑降水(U2)、基坑开挖(U3)、外加人为因素(U4)、自然因素(U5)、水文地质因素(U6)和周围环境因素(U7)等因素，将它们作为二级指标，分析确定每道工序下的风险因素作为三级指标，建立如图3所示的基坑风险评估指标体系。

图3 风险指标体系

2.3 模糊DEMATEL分析

基于模糊DEMATEL法，考虑各指标间的相互关系计算它们的权重。邀请5位地下工程领域经验丰富的专家按照表1的规则对各指标进行相对重要性评价，构造模糊直接影响关系矩阵，矩阵中的元素由专家评语转化而来的三角模糊数，再经过1.1节中一系列矩阵转换得到综合关系矩阵以及各指标的影响程度fi、被影响程度ei、原因度Fi和中心度Ei结果如表3和表4所示。

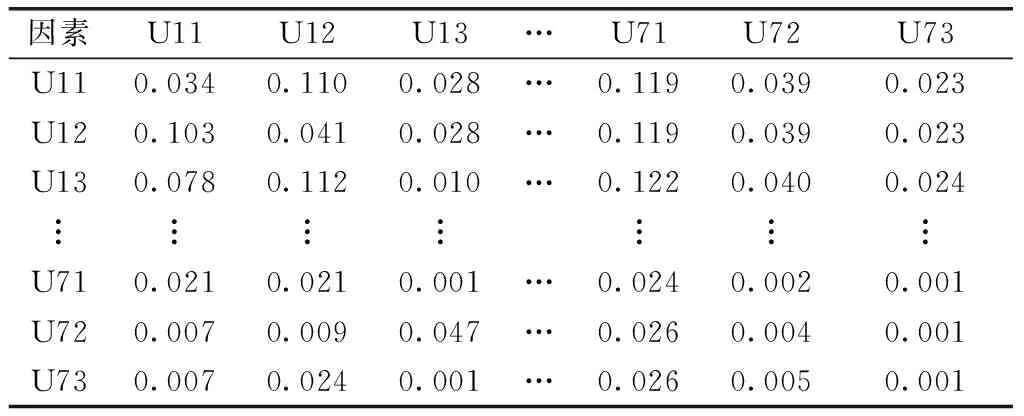
表3 综合关系矩阵

基于表4绘制出各指标间的因果关系图，如图4所示，横轴为中心度，代表各指标的重要程度。纵轴为原因度，正值代表对其他因素有影响，负值表示受其他因素影响。根据图4可以看出，基坑渗漏U21,突涌水U34为两个指标的重要度最高，说明它们是影响基坑施工安全性的两个重要因素，这也符合济南地区地下水丰富，基坑施工过程中经常发生渗漏、涌水的情况。原因度为正，风险指标属于原因组，原因度为负则风险指标属于影响组。U73、U61、U52、U51、U14、U35、U41、U22、U13、U34等风险指标属于原因组，U73、U72、U31、U33、U62、U71、U11、U23、U32、U12、U21等风险指标属于影响组。可以看出超挖欠挖U12、管理疏忽U15是影响程度较高的两个因素，说明其对其他因素有很大的影响，比如超挖欠挖会导致维护结构变形、支撑失稳甚至基坑发生倒塌，管理上做到称职同样能够避免一些因人员自身原因导致的风险事故的发生。

表4 中心度与原因度

图4 因果关系图

从表3关系矩阵中导出网络关系图(图5)，由于各因素间的联系复杂，图5中只描述了基坑围护与支撑、基坑降水、基坑开挖三部分因素间的网络关系。将各指标分为影响组和被影响组，椭圆代表影响组，矩形代表被影响组，再用箭头将有相互联系的因素连接起来，代表一个因素受另外一个因素影响，双向箭头代表因素之间互相影响。它清楚地展示了各指标间的复杂关系。

图5 网络关系图

在获得各指标的重要度及相互影响关系后，根据式(11)确定各指标的权重，如表5所示。权重最高的几个风险指标为维护结构变形U12、基坑渗漏U21、坍塌U32、突涌水U34，这也表示这几个风险是最大的。如维护结构变形占有较大权重，因为维护结构变形会导致周围地表发生沉降进而使得附近建筑物发生沉降开裂，甚至严重的有倒塌的风险。对基坑本身而言，围护结构变形过大使得支护结构失稳，严重影响基坑稳定性，处置不及时基坑有发生坍塌的风险。同时桩体强度不足、插入深度不够、支撑不及时，开挖速度过快、超挖等会导致维护结构变形。可以看出采用模糊DEMATEL法，考虑各指标间的相互关系来计算其权重是较为合理的。

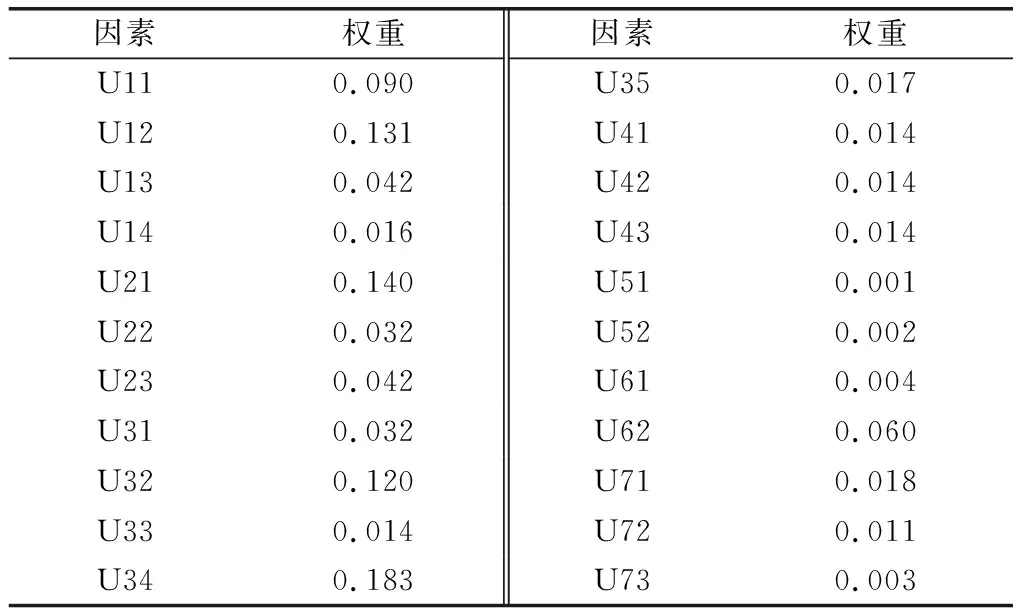
表5 权重结果

2.4 TOPSIS综合评判

根据风险评估指标体系，分别从风险发生的概率P以及风险发生造成的损失C两方面对各指标进行评分，评分规则参照城市轨道交通工程风险管理规范，最终风险值为概率值P与损失值C的乘积。构建初始评判矩阵，矩阵的元素为概率P与损失C的乘积。经过1.2节系列计算得到各评价指标的正负理想解以及贴近度，对其作出重要性排序，结果如表6所示。

由表6贴近度的排序结果可知，突涌水的贴近度最大，是本基坑工程中最为关键的风险指标。济南地区地下水丰富，补给充足且承压水头高，突涌水是深大基坑开挖时常遇的风险，给基坑稳定性造成重大影响，风险一旦发生可能会导致基坑开裂、坍塌等严重事故，因此在施工过程中需要特别注意突涌水的防范。此外基坑渗漏、维护结构变形、坍塌等指标的贴近度也相对较高，也是应重点防范的风险事故，由表4可知，它们的原因度小于零，说明它们受其他指标因素影响较大，因此在施工过程中及时采取相关防治措施能够避免这些事故的发生。

表6 TOPSIS计算结果

在对风险指标进行优先排序后，通过式(17)结合各风险指标的权重和贴近度求得基坑整体风险值为0.395，为于二级风险，属于可以被接受的范围，需要加强日常管理与监测避免风险事故的发生。

3 结论

(1)基于模糊DEMATEL理论的权重计算方法，既考虑了深基坑施工过程中风险因素的模糊性，又考虑了各风险因素间的相互联系。这样的权重计算方法更加合理且符合工程实际情况。

(2)引入TOPSIS理论对基坑风险因素进行重要性排序，得到本基坑施工过程中最为关键的风险因素是突涌水事故，需要做出针对性的防范措施，保证基坑工程施工的顺利进行。

(3)提出一种基于模糊DEMATEL和TOPSIS理论的地铁车站深基坑风险评价模型，并对烈士陵园站进行了施工风险分析，得到该基坑施工风险值为0.395，风险等级为Ⅱ级，处于可以接受范围，与施工现场实际情况相符合，证明了该模型的可行性。