扰动条件下车载氢能源监测系统效能评估

李艳昆，刘晗

(1.中车青岛四方机车车辆股份有限公司，青岛 266111；2.煤炭科学研究总院有限公司，北京 100013)

随着能源转型、生态环境改善的日趋紧迫，氢能在全球范围内的能源地位也越来越明晰。广泛使用氢能不仅有助于减少碳排放，同时有助于能源安全和可持续利用[1]。近年来，世界各国政府及铁路部门都致力于研究氢能及燃料电池技术，从而实现未来战略性减排目标。例如，截至2019年底，中国加氢站超过50座，在建10多座，规划中的加氢站数十座；到“十四五”末，中国加氢站数量可能超过150座[2]。从2020年起，氢动力列车将成为英国火车轨道上的新标准运输方式，将与2040年彻底摆脱柴油动力火车的举措共同完成；德国已有两辆氢气火车且每天可行驶近800 km，并计划在2021年前将氢气火车数量扩大到14辆[3]。然而，由于氢气的密度很小，高压氢气储运设备中的氢气极易泄漏。如果在开放空间，对安全有利，但是一旦散逸受阻，大量氢气积聚，可能造成人员窒息。此外，因超温、充装过量等原因，设备有可能强度不足而发生超压爆炸。在车载氢能源安全监测理论方面，Pahon 等[4]基于电堆电压信号、电池电压信号和气压降信号特点，采用小波变换的方法快速诊断质子交换膜燃料电池系统故障；Filonenko等[5]将超声波监测与到达时间差异的三边测量方法相结合，提出了监测装置设计的准确优化方法；An等[6]开发一个可靠的传感器定位模型，旨在优化传感器的位置，以便在传感器可能中断的风险下最大限度地提高物体定位/监视的准确性。Li等[7]应用响应面方法(response surface methodology,RSM)来获得用于评估传感器性能的优化公式，并通过方差分析(analysis of variance,ANOVA)评估单个因素对传感器效能的影响。Sterl等[8]通过系统研究耦合钯纳米结构的几何形状及光学特征，制定了有效优化氢敏感性的设计规则，并对浓度低至 100 ppm(1 ppm为百万分之一)的氢气进行了准确检测。国内对于氢能源监测系统效能研究相对较少。熊秋芬[9]基于故障树诊断算法，对燃料电池发动机中的传感器故障进行诊断、仿真分析和验证。杨太华等[10]基于故障树和改进灰色关联法，建立加氢站的安全风险评价指标体系,对加氢站建设和管理提出更加有效的风险防控的措施。为了保证氢能源系统的安全、可靠和经济运行，李鹏等[11]在水汽质量控制标准和化学监督技术导则下，对监测系统化学控制和监测设计与优化进行研究。任普等[12]基于大数据的健康监测系统平台,对设施服役性能与安全状态进行评估和实时预警。张可健等[13]融合了机理建模和辨识建模方法，通过建立氢燃料电池系统模型，得出不同参数的变化对燃料电池运行态势的影响结果。然而，氢能源系统安全监测过程常常出现信号到达率超过系统负荷或者监测设备由于外部扰动条件产生的监测结果不准确等情况，在现有文献中很少被考虑。忽视系统排队饱和因素或监测过程扰动因素，将导致对安全监测系统效能的过高估计，非常不利于安全隐患的及时消除。

基于此，现提出监测过程扰动条件下车载氢能源安全监测系统效能评估方法。当需求监测的优先级与紧急程度相关时，监测系统需要将高等级信号优先，保证监测系统的安全性与有效性。为了对系统效能科学评估，设计一种容量有限的优先排队机制。数值结果表明，车载氢能源安全监测装置的可靠性因素，能够对安全监测系统效能产生显著影响；忽略这些因素可能会导致系统效能的不准确描述与评估。此外，对系统失效损失和排队成本相对于监测器可靠性概率进行了敏感性分析，以期为车载氢能源安全监测系统设计提供技术支持与控制策略参考。

1 模型基本假设

提出车载氢能源安全监测系统评估方法的基本假设，从而根据系统排队均衡条件下的稳态概率，计算系统的监测效能指标。在车载氢安全监测系统中，接收氢气浓度传感器发送的氢瓶和电堆氢气浓度信号、温度信号、进堆氢气压力信号和进堆空气压力信号等，根据预置的氢安全监测系统故障诊断策略，将风险信号等级传输至车载控制器。根据氢能源安全监测装置的概率性状态，将其分为空闲(用0表示)和忙碌(用1表示)两种状态。因此，一个含有N个安全监测装置的车载氢能源系统的可能状态总数为2N个。例如，车载氢能源监测系统状态{110}表示系统的3个安全监测装置状态分别为忙碌、忙碌和空闲。通过计算每一个可能的车载氢能源监测系统状态概率，评估监测系统总效能(如系统监测丢失率、负荷程度以及响应频率)。车载氢能源安全监测系统排队均衡的假设如下。

(1)监测信号生成J个监测区域，信号的发生率遵循泊松分布且相互独立。

(2)每个监测区域预先确定监测任务响应顺序。优先响应的监测装置(通常是距离监测区域最近的监测装置或功能最符合响应类型的监测装置)安排在第一响应顺序。如果此监测装置处于忙碌状态，则将调度响应顺序中的下一个优先监测器。如果响应顺序列表中的所有监测装置都处于忙碌状态，则认为监测目标丢失或转移到另一个监测系统中。

(3)每个监测装置的服务时间遵循负指数分布，以保证排队均衡的马尔科夫过程具有非记忆性。

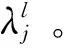
(5)每个监测装置都作为一个独立的监测器。系统中共有N个常规监测器，包括高级常规监测器和基本常规监测器；另有V个后备监测器。常规监测器n和后备监测器v的服务时间分别服从比率μn和μv的负指数分布。

(6)后备监测器因响应顺序较低，在全部常规监测器都不可用时，才能进行监测。

(7)常规监测器是完全可靠的，这意味着没有服务扰动。相比之下，后备监测器可能出现服务扰动情况，因此处于空闲、忙碌或中断3种状态之一。因此，系统排队均衡状态空间中总共有2N×3V种可能状态。

(8)在监测设备正在响应低级别信号时，监测系统允许优先级较高的排队信号优先被响应。响应策略如图1所示。

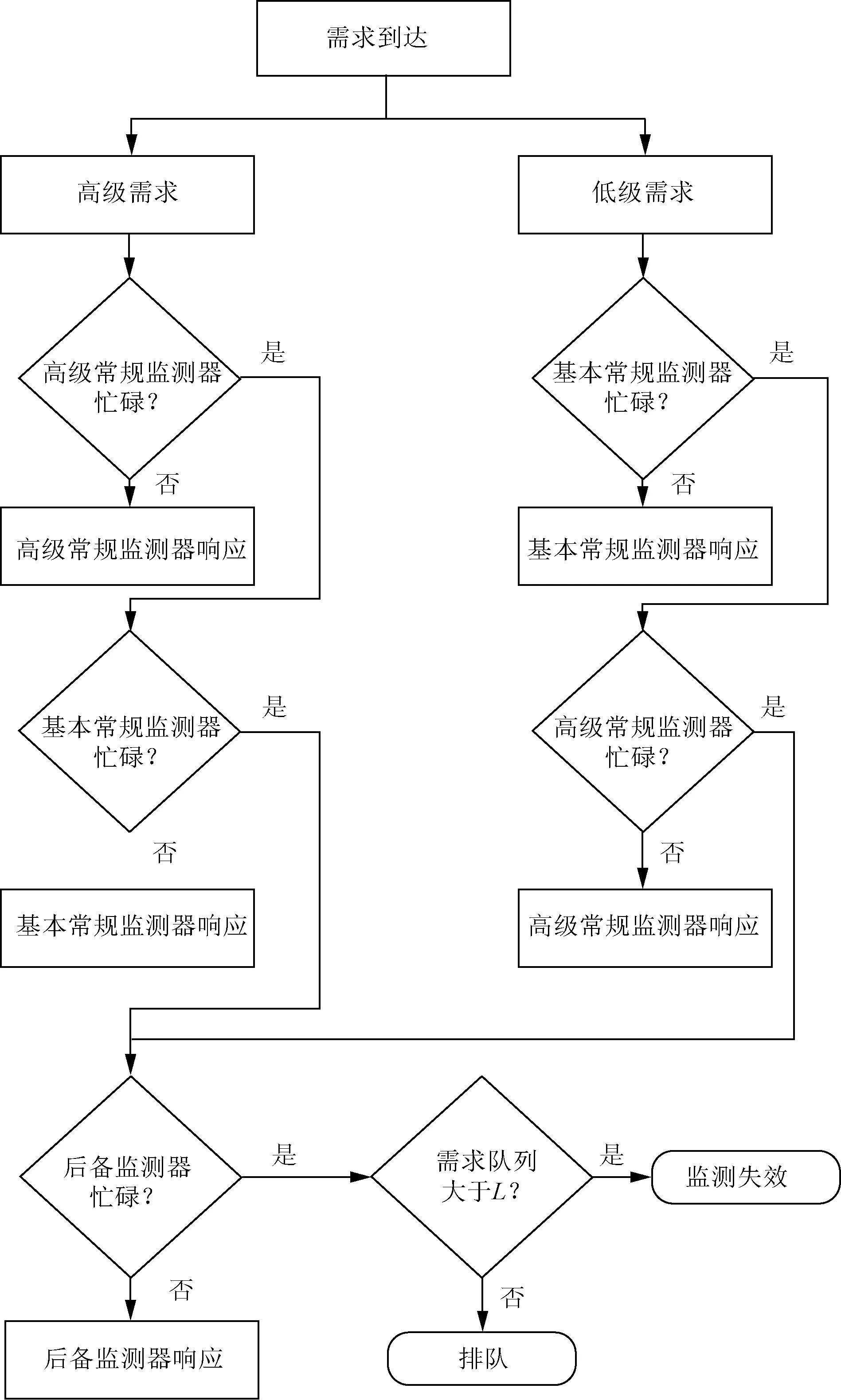
图1 车载氢能源安全监测系统响应策略

2 车载氢安全监测系统排队均衡模型构建

为了描述在监测系统排队平衡下监测响应机制，以含有2个常规监测器(基本级别的监测器n1服务率为μ1，高等级别的监测器n2服务率为μ2)和1个后备监测器(用v表示)的监测系统为例进行说明。两个监测区域分别生成低级别信号λ1和高级别信号λ2。

表2显示了监测系统的响应顺序列表。常规监测器优先于后备监测器，对信号进行响应。如果两个常规监测器均处于忙碌状态，系统将收到的新信号时传送至后备监测器。

表2 系统监测装置响应优先顺序列表

图2(a)显示了常规监测器系统的可能性均衡状态，其中23种状态有条件地相互转移，且当所有监测器都忙碌时出现系统监测失效情况。图 2(b)显示了考虑后备监测器中断和排队优先级条件下的可能性均衡状态，即所有常规监测器都不可用时，才会传送需求至后备监测器。如果该后备监测器可靠，则由其进行监测任务；否则，将出现一个需求队列，直到常规监测器从忙碌状态转移到空闲状态。由图可知，相比于传统的常规监测器系统，含有后备监测器的系统均衡状态发生了结构性变化。后备监测器可靠性和需求等待状态下可能状态的系统均衡方程如下。

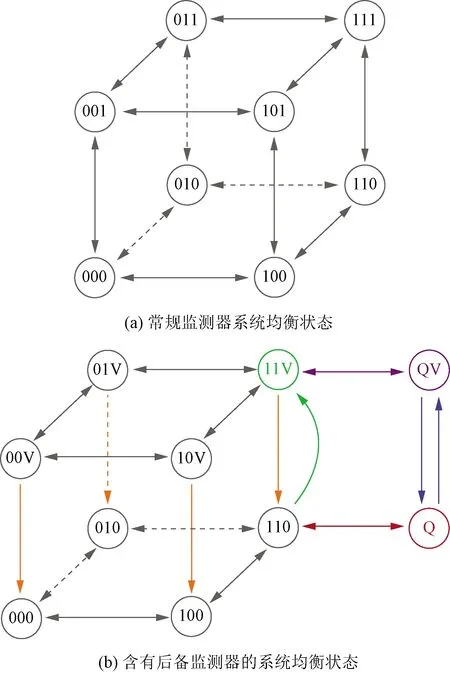
0为监测器处于空闲状态；1为监测器处于服务状态；Q为系统处于排队状态；V为后备检测器处于服务状态

(λ1+λ2)P00=μ2P01+μ1P10+μvP00vb+μvP00va

(1)

(λ1+λ2+μ2)P01=μ1P11+λ2P00+

μvP01vb+μvP01va

(2)

(μ1+μ2+λ1+λ2)P11=μvP11va+μvP11vb+

(μ1+μ2)P11b+(μ1+μ2)P11a+

(λ1+λ2)P10+(λ1+λ2)P01

(3)

(λ1+λ2+μ1)P10=μvP10va+μvP10vb+

λ1P00+μ2P11

(4)

(λ1+λ2+μv)P00va=μ2P01va+μ1P10va

(5)

(λ1+λ2+μv)P00vb=μ2P01vb+μ1P10vb

(6)

(λ1+λ2+μ2+μv)P01va=λ2P00va+μ1P11va

(7)

(λ1+λ2+μ2+μv)P01vb=λ2P00vb+μ1P11vb

(8)

(λ1+λ2+μ1+μv)P10va=λ1P00va+μ2P11va

(9)

(λ1+λ2+μ1+μv)P10vb=λ1,tP00vb+μ2P11vb

(10)

(λ1+λ2+μ1+μ2+μv)P11va=

(λ1+λ2)P01va+(μ1+μ2+μv)P11va,A+

(μ1+μ2)P11va,B+(μvα2)P11vb,A+

(λ1+λ2)P10va+(λ2α2)P11

(11)

(λ1+λ2+μ1+μ2+μv)P11vb=

(λ1+λ2)P01vb+μvP11va,B+

(μ1+μ2)P11vb,A+(μ1+μ2+μv)P11vb,B+

(λ1+λ2)P10vb+(λ1α1)P11

(12)

(μ1+μ2+μv)P11va,A=λ2P11va

(13)

(μ1+μ2+μv)P11va,B=λ1P11va+(λ2α2)P11b

(14)

(μ1+μ2+μv)P11vb,A=λ2P11vb+λ1α1P11a

(15)

(μ1+μ2+μv)P11vb,B=λ1P11vb+(λ1α2)P11b

(16)

[μ1+μ2+α2(λ1+λ2)]P11b=λ1(1-α1)P11

(17)

(μ1+μ2+α1λ1)P11a=μv(1-α2)

P11vb,A+λ2(1-α2)P11

(18)

(19)

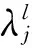
以式(3)为例，{11}为当前状态，表示常规监测器均处于忙碌状态。公式左边表示当前状态转移至其他状态的概率。系统状态发生转移，当且仅当：①低级别信号λ1或高级别信号λ2到达时；②常规监测器n1或n2完成正在进行响应任务后。

式(3)右边为其他所有可能状态(包括{11va}、{11vb}、{11b}、{11a}、{10} 和{01}等状态)转移至当前状态的概率。{11va}表示常规监测器处于忙碌状态，后备监测器正在服务高级别信号。包含以下情况：①当后备监测器v完成高级别信号监测后，系统状态由{11va} 转移至{11};②当后备监测器v完成低级别信号监测后，系统状态由{11vb} 转移至{11};③当常规监测器n1或n2完成当前监测任务并开始服务排队系统中的低级别信号时，系统状态由{11b} 转移至{11};④当常规监测器n1或n2完成当前监测任务并开始服务排队系统中的高级别信号时，系统状态由{11a} 转移至 {11};⑤当低级别信号λ1或高级别信号λ2到达时，系统状态由{10}转移至 {11};⑥当低级别信号λ1或高级别信号λ2到达时，系统状态由{01}转移至{11}。

3 安全监测系统效能指标评估与敏感性分析

满足等式(1)～式(19)的稳态概率，能够对安全监测系统效能指标进行准确评估，计算系统无法响应损失、监测器工作负载和信号排队等待成本。

后备监测器v的工作量，记为Wv，可以通过将后备监测器繁忙状态的概率相加，从排队均衡方程中计算出来，即

Wv=P00va+P00vb+P01va+P01vb+

P10va+P10vb+P11va+P11vb+P11vaA+

P11vaB+P11vbA+P11vbB+P11b+P11a

(20)

式(20)中：va为备用监测器服务于a类需求；vb为备用监测器服务于b类需求。

Loss1表示由于后备监测器中断导致队列中信号无法正常监测导致的损失概率。此项指标能够通过识别特定状态集合计算，其中特定状态为响应顺序列表中所有监测器均忙碌或收到扰动的状态，即

Loss1={λb[P11vaA+P11vaB+P11vbA+P11vbB+

P11b(1-α2)+P11a(1-α1)}+

λa[P11vaA+P11vaB+P11vbA+P11vbB+

P11b(1-α2)+P11a]/(λb+λa)

(21)

信号因等待导致的监测失效损失概率指标Loss2为

Loss2=πT

(22)

(23)

式(23)中：L为队列中的平均用户数。

L=P11VaA+P11VaB+P11VbA+P11VbB+P11b+P11a

(24)

由此，推导出

(25)

并得到此项系统效能指标:

(26)

基础需求和高级需求占总需求的比例不同，可能对系统性能产生潜在差异性影响。将高级需求到达率与基础需求到达率的比率定义为到达率比(arriving，ARR)。设置场景I、II和III，其中 ARR 分别为 1/5(λ1=0.2;λ2=1.0)、1(λ1=λ2=0.6)、5(λ1=1.0;λ2=0.2)。系统中2个常规监测器和1个后备监测器的服务率分别为μ1=μ2=0.8 和μv=0.6。

图3 显示，在3种情景中，不同后备监测器可靠性概率下的系统失效损失成本和信号等待成本。此案例中的αB与αA分别代表通用模型中的α1与α2。可以观测到，如果监测区域生成更频繁信号，则响应优先顺序列表中候选监测器可靠性的边际效益将增加。具体来讲，在场景一[图 3(a)]中，当高级需求更加频繁时，高级别常规监测器的可靠性对系统损失控制产生更大影响。在场景二[图3(b)]中，低级别常规监测器的可靠性，相比于场景I中的作用更显着，但仍然没有超过高级别常规监测器可靠性对系统损失控制的影响。高级别常规监测器不仅服务于高级需求，也服务于低级需求，这在一定程度上加强了高级别常规监测器的可靠性效应。在场景三[图 3(c)]中，低级别常规监测器可靠性的影响超过了高级别常规监测器，并在3个场景中将其提升到最高。特别的，高级别常规监测器的可靠性对系统等待成本的影响是有限的。造成这种结果的原因是，高级别常规监测器被动地为高级需求提供监测，这些需求在队列中比基本需求具有更高的优先级，从而导致更长的等待时间，以及更多数量的基本需求监测失效。

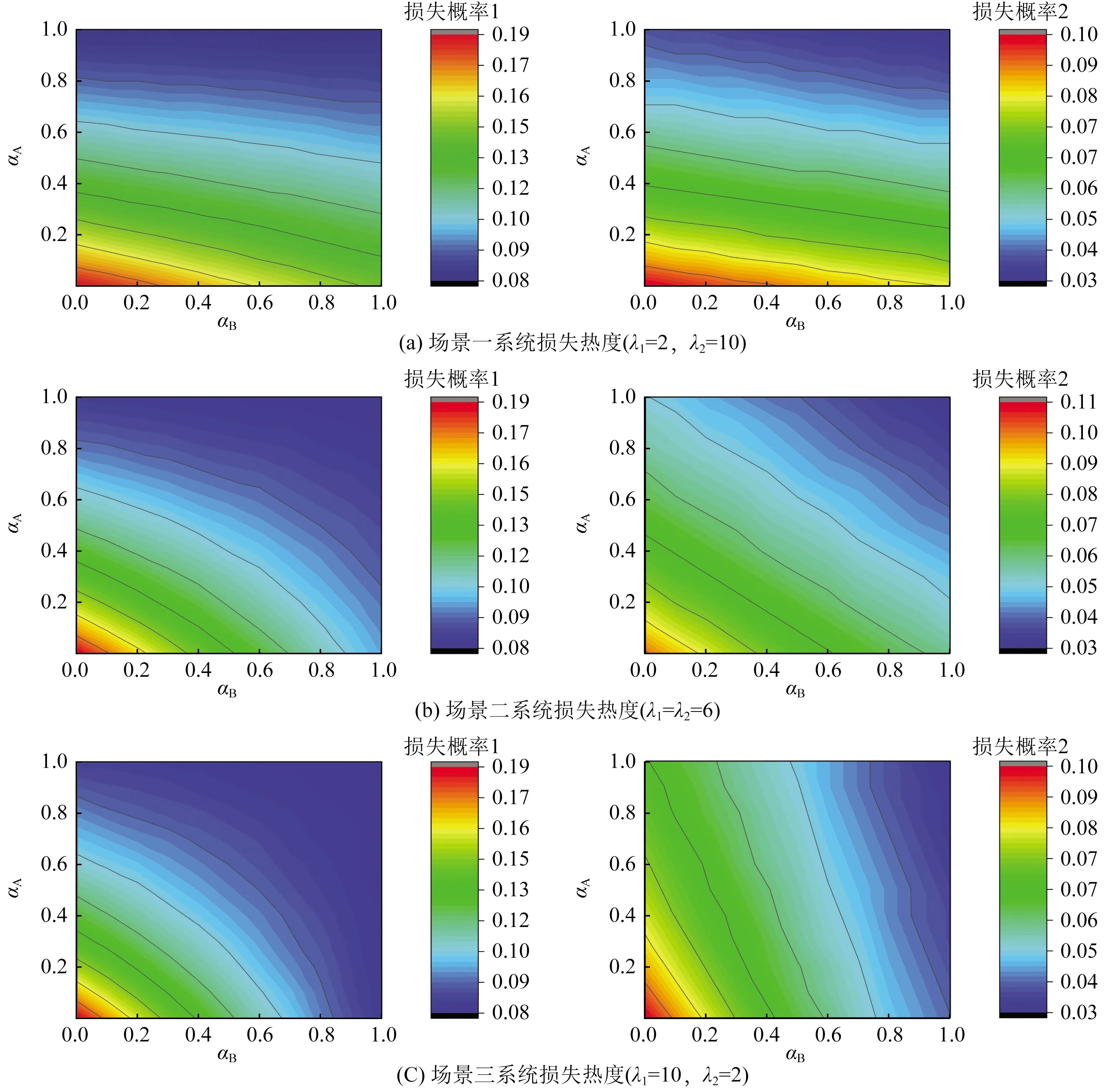
图3 后备监测器扰动条件下系统损失热度图

结果表明，不同 ARR条件下的可靠性概率对系统成本有不同的影响。敏感性分析说明了含有常规监测器和后备监测器的氢能源监测系统对不同场景下系统损失的可靠性影响。通过提高后备监测装置可靠性概率，系统性能得到有效的损失控制。

4 结论

基于监测系统优先响应顺序与后备监测装置的可靠性条件，提出了车载氢能源安全监测系统效能评估模型，并针对多场景后备监测器的可靠性概率，对系统损失进行了敏感性分析。结果表明，不同 ARR 可靠性概率对系统成本产生显著的差异性影响。通过提高后备监测装置可靠性概率，系统性能得到有效的损失控制。敏感性分析结果可为车载氢能源安全监测系统的设计与可靠性成本投入提供重要决策参考。

由于仅对常规监测器和后备监测器进行了独立响应规则设计，没有考虑两类监测器进行更加深入的协同性设计与相关分析。在未来研究中，可对氢能源安全监测系统进行更加精细化的结构性设计，使本文提出的方法具有更加广泛的适用性。