空间分辨率对上行先导起始过程数值模拟的影响

裴晓芳，丁洁，郭秀峰,,4*，纪梓煜，陈佳祥，张超凡，范阳

(1.南京信息工程大学电子与信息工程学院，南京 210044；2.无锡学院大气与遥感学院，无锡 214105；3.南京信息工程大学江苏省大气环境与装备技术协同创新中心，南京 210044；4.中国气象科学研究院灾害天气国家重点实验室，北京 100081)

随着社会的发展，由雷电造成的人身安全问题及经济财产损失越来越多，对此合理的规避由雷电造成的损失显得尤为重要[1-5]。在雷暴期间，建筑物上能否始发上行先导是判断其是否能被闪电击中的一个标准。因此，无论在雷电物理研究还是雷电防护领域，物体上如何发生上行先导是一个关键的问题。随着计算机技术的发展，目前对于上行先导的研究，除了对闪电的直接观测和实验室实验模拟之外，数值模拟成为当下广泛使用的一种研究手段。在数值模拟中，连续的空间被划分成离散的网格，进而计算每一个网格上的物理量。如何选取合适的网格大小(也称空间分辨率)是所有数值模拟中的一个重要问题。因此，在上行先导数值模拟研究中，选取合理的上行先导始发判据和合适的空间分辨率都是至关重要的。

基于20世纪70年代Les Renardieres Group(“狐狸”团队)开展的一系列正极性长空气间隙放电实验，分析提出了上行先导的起始可分为电晕起始、正先导始发和传播三个阶段。基于此，学者们提出了不同的闪电物理概念模型，这些模型利用实验室长火花的定量结果来预测下行和上行先导的发展[6-11]。近些年，也有学者提出了更简便的3种先导起始判据[12-14]。分别是平均电场判据、临界长度判据和初始流注动态临界长度判据。这些判据主要是用宏观参量代替了先导发展的复杂计算过程。但是在这些模型中，被广泛沿用至今的上行正先导始发判据主要有以下4种：介质击穿模型、临界半径准则、临界长度法和临界电场法。

介质击穿模型(dielectric breakdown model,DBM)是Niemeyer等[15]和Wiesmann等[16]开发的用于模拟雷暴云中放电通道的宏观性质和地面物体尖端的放电通道。先导的产生和传播判据是导体或尖端周围的电场是否超过临界电场阈值(Ecrit)。但是临界电场阈值在不同的模型中是不同的，例如，在云中临界电场阈值Ecrit=100 kV/m[17]、Ecrit=150 kV/m[18]，以及在物体尖端临界电场值Ecrit=500 kV/m[10]。此外，这个模型不能够模拟微观物理击穿过程。

临界半径法与DBM相似，当尖端电场等于电晕初始电场(通常Ecrit=3 000 kV/m)时，就可以达到稳定的先导初始条件。这一标准是基于文献[19]的实验结果，并在文献[6-8]的模型中得到应用。由于这个概念是通过高压实验室长间隙放电实验得到的，所以是否适用于自然雷电在更大维度范围内产生的上行先导还不清楚[20]。

临界长度法是由Petrov等[10]提出的根据上行先导流光区电场强度以及长度提出的判据。该方法认为当流光区长度发展达到了0.7 m，并且同时这个范围里的电场强度超过了正极性流光区的平均电场值(约为500 kV/m)，则流光带转化为先导。

然而，以上3个标准对实验结果无法体现先导发展的具体物理过程。因此，Becerra等[21-23]开发了一个自持式上行先导始发模型，该模型遵循了Goellian等[24]类似的方法。此标准中，当流光区能产生大于或等于1 μC电晕电荷时[25-26]，方可形成不稳定先导，而稳定先导持续传播的条件是不稳定的先导长度达到2 m。尽管最后这个标准被认为是这4个标准里面最合理的，它仍旧不能应用于所有的数值模拟中。例如，在模拟先导分支结构或模拟区域太大而无法使用精细的空间分辨率时(当最小网格的尺寸大于2 m)。因此，另外3种标准仍被广泛使用。

但是，无论选择哪种标准，首先都要计算避雷针尖端或物体尖端周围的电势或电场值。目前在大多数的先导模型中，主流模型采用的电位计算方法有有限差分法(finite difference method，FDM)、有限元法(finite element method，FEM)和电荷模拟法(charge simulation method，CSM)。由于可以模拟复杂边界，FDM和FEM是两种主要的方法。谭涌波等[27]在二维模型中采用FDM的方法，得出在相同建筑物形状下尖端增强的电场实际上是相同的，但是在数值模拟中受网格大小的影响很大。网格尺寸越小，计算出的电场越大，尤其是在尖端处。因此，在上行先导模型中，网格的大小会影响对先导始发的判断。然而以上4种判据都是基于实验结果的，模拟中并没有考虑网格大小对判据的影响。

此外，为了模拟雷暴云下的地面物体产生的上行先导，模拟域范围至少要达到公里的量级，而建筑物接闪杆尖端通常仅有几厘米。通常来说，空间分辨率越高模拟越精确，但实际上，特别是在三维(3D)闪电先导起始和传播模型中，很难对大范围(几千米甚至几十千米)进行非常小的网格(cm或mm)剖分。进而导致，学者们对数值模拟的定量计算结果一直持有怀疑态度。因此，如何选择合适的网格大小是模拟上行先导始发的关键问题。换句话说，当网格的最小尺寸固定时，应该选择怎样的先导起始判据？但是现在对这一问题的研究讨论较少。

为探讨被广泛沿用至今的4种先导起始判据，在不同空间分辨率模拟中的适用性，以提高上行先导数值模拟的可靠性。基于有限差分法，现建立一个计算建筑物周围电场的3D变网格模型，分析网格大小与电场计算结果的关系，并取了3种不同建筑物高度，讨论网格大小对4种先导起始判据的影响。最后，在此基础上提出网格大小的选择方法和不同始发判据在实际先导模拟中的适用性。

1 模型及计算方法介绍

1.1 模型建立

由于先导起始的判断，均离不开精确的尖端电场计算。因此，为了更加精确地模拟建筑物周围电场的分布特征，现基于有限差分法求解泊松方程，建立了三维变网格下的静电场计算模型[28-32]。相对之前的研究，本文研究主要有两点优势：三维模型克服了二维模型对实际三维空间模拟的不足；变网格技术克服了均匀网格对大模拟域中细小尖端的模拟不足。

使用变网格技术，在尖端处采用小网格，离尖端越远网格按照一定比例逐渐增大，如图1所示，以xy平面为例，尖端顶部范围内采用最小网格，后续按照比例增加。模拟域为地面上空500 m×500 m×500 m。仅考虑建筑物上尖端的特征而不考虑建筑物本身的几何特征，因此将建筑物尖端模型简化为一个接地的立方体形状的理想导体，长、宽、高分别为20 cm、20 cm、200 m，位于模拟域的中间。此外，还建立了100 m和300 m高的建筑物模型。在雷暴云电场(Eb)下，近地面的电场可近似为均匀的垂直电场，同时不考虑空中自由电荷的存在。因此，在实际的电场计算时，建筑物尖端周围的电场可通过求解已知边界的拉普拉斯方程获得，拉普拉斯方程为

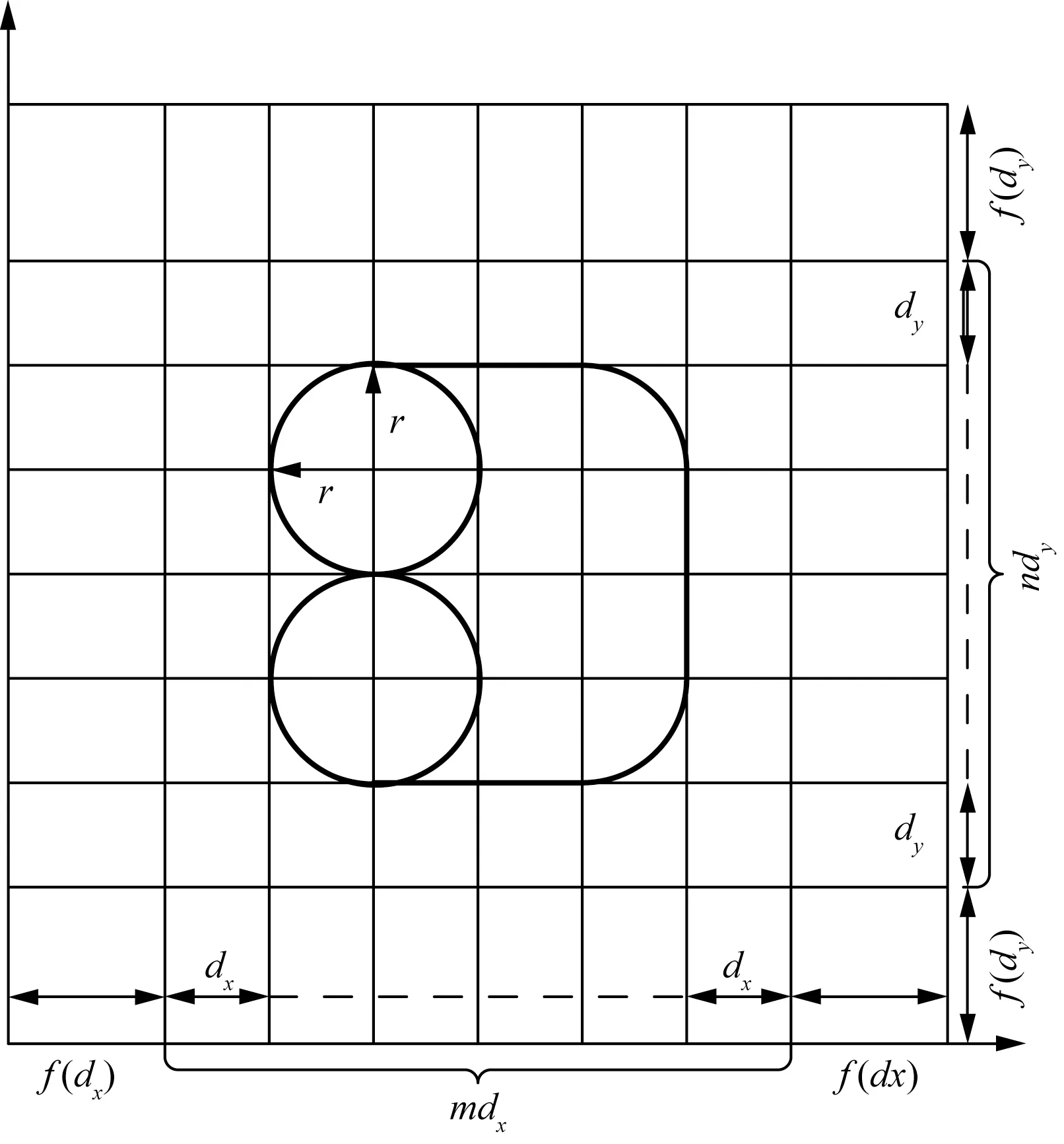
r为避雷针边缘半径；dx、dy分别为建筑物在x、y方向上划分的最小网格长度；m、n分别为建筑物在x、y方向上划分的网格数量；f(dx)、f(dy)分别为关于dx与dy的函数，用来做变网格划分

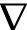
(1)

将模拟域的上边界设置为第一类边界，顶边界的电位值φ(z= 500 m)为固定值，φ=zEb=-5 000 kV；底边界为地面和建筑物尖端，也为第一类边界，φ=0；其他4个侧面均为第二类边界，电位梯度在边界上法向分量为0。由于，网格较多，采用超松弛迭代法求解变网格下的三维有限差分方程，从而获得空间每个格点上的电位值，进而根据式(2)求得电场强度。

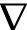
(2)

式(2)中：E为电场值，V/m。

1.2 模型验证

为了验证本文基于有限差分法建立的三维变网格电场计算模型的计算结果，利用基于有限元法的Comsol 软件对上节所述的雷暴云电场下的建筑物尖端周围的电场进行了计算。由于尖端处的网格尺寸大小，直接影响计算结果，而远离尖端时，网格尺寸对尖端处的电场计算精度则影响较小。因此，在网格剖分时，则要保证尖端处的网格尺寸大小相当。本文模型采用长方体对空间进行离散，在尖端处网格尺寸最小，为0.1 m，随后逐步变大，最大网格尺寸为22.261 m；Comsol软件中，采用四面体对空间进行离散，为了同本模型的结果对比，尖端处的最小网格尺寸也为0.1 m，随后进行自由剖分，最大网格尺寸为20 m。以此网格剖分为例，利用上述两种方法计算建筑物尖端周围的电场大小。结果如图2所示，当环境电场为-10 kV/m 时，尖端上空电场随高度的变化特征。不难发现，两者计算结果基本相同。由此可见，本文建立的三维变网格电场计算模型的计算结果可靠。

图2 背景电场为-10 kV/m时尖端上方的电场变化特征

2 空间分辨率对先导起始的判据的影响

2.1 介质击穿模型和临界半径准则

地面突出物(如树木、房屋等)及地形的起伏都会对其周围的大气电场产生畸变作用，地面突出物周围的电场值与环境电场值的比值称为电场畸变系数[33-34]。基于本文模型的数据，不同空间分辨率下建筑物尖端拐角表面上方的电场畸变系数随高度的变化曲线图，如图3所示。

由图3可以看出，同一空间分辨率下尖端拐角表面上方的电场畸变系数值在1 m范围内随高度迅速下降，且不同空间分辨率下尖端处电场畸变系数的值相差巨大，尖端网格划分越细，尖端上方的电场畸变系数就越大。介质击穿模型和临界半径准则皆是以导体或尖端表面的电场是否超过临界电场阈值来作为先导起始的判据。介质击穿模型在云中临界电场阈值取Ecrit=100 kV/m的判据是根据实验中在3个维度上网格间距皆取125 m得到的[11]。而云中临界电场阈值Ecrit=150 kV/m的判据来自空间分辨率12.5 m[15]。临界半径准则的实验室证明保持着7 m的恒定电极，并认为对于具有球形和圆柱对称特征的电极临界半径在35 cm和10 cm左右趋于饱和。所以在使用这两种判据进行数值模拟研究中对先导起始和传播的研究时，会由于空间分辨率选取过大使得尖端表面电场计算值较小，从而导致判断时先导难以始发，而空间分辨率选取过小时则会导致判断先导过早产生。

ki为电场畸变系数；H为高度；hmin为空间分辨率

由于在数值模拟中，由一定空间分辨率所引起的系统误差是一个固定的值，它与分辨率有关，而与建筑物结构尺寸无关[35-36]。所以在使用这两种判据时，可以假定0.01 m或更精细空间分辨率下计算出的尖端表面电场为标准实际电场值，将0.02、0.05、0.1 m等空间分辨率下尖端处的电场值与标准值相比进行修正，将得到的数个修正系数进行拟合，得到修正系数的拟合曲线图。在之后采用过大空间分辨率的数值模拟研究中，可在拟合的修正系数曲线图上得到修正系数，从而得到不同空间分辨率对应的合适的判断先导始发的尖端电场值，具体方法可参见文献[37]。

2.2 Petrov 临界长度法

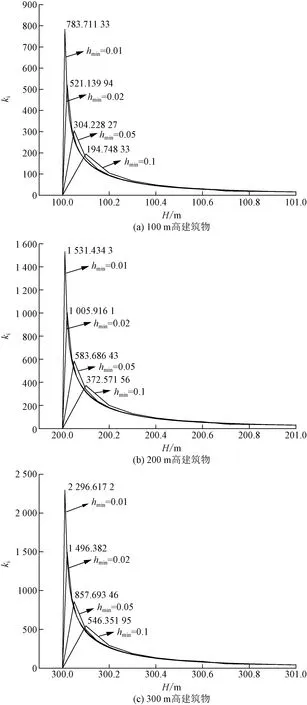
Petrov根据确定垂直桅杆的雷击距离实验，提出了上行先导始发判据。认为当流光区长度达到了0.7 m，并且同时流光区内的电场强度超过了正极性流光区的平均电场值(约500 kV/m)，流光完成向先导状态的转化，认为上行先导起始。基于本文模型，更改不同空间分辨率下背景电场值，使满足0.7 m范围内电场强度皆超过500 kV/m。根据数据作出尖端拐角上方电场随高度变化的曲线图，如图4所示，建筑物高100、200、300 m时当最小空间分辨率分别取0.01、0.02、0.05、0.1 m时，根据Petrov临界长度法均可判断此时上行先导起始。

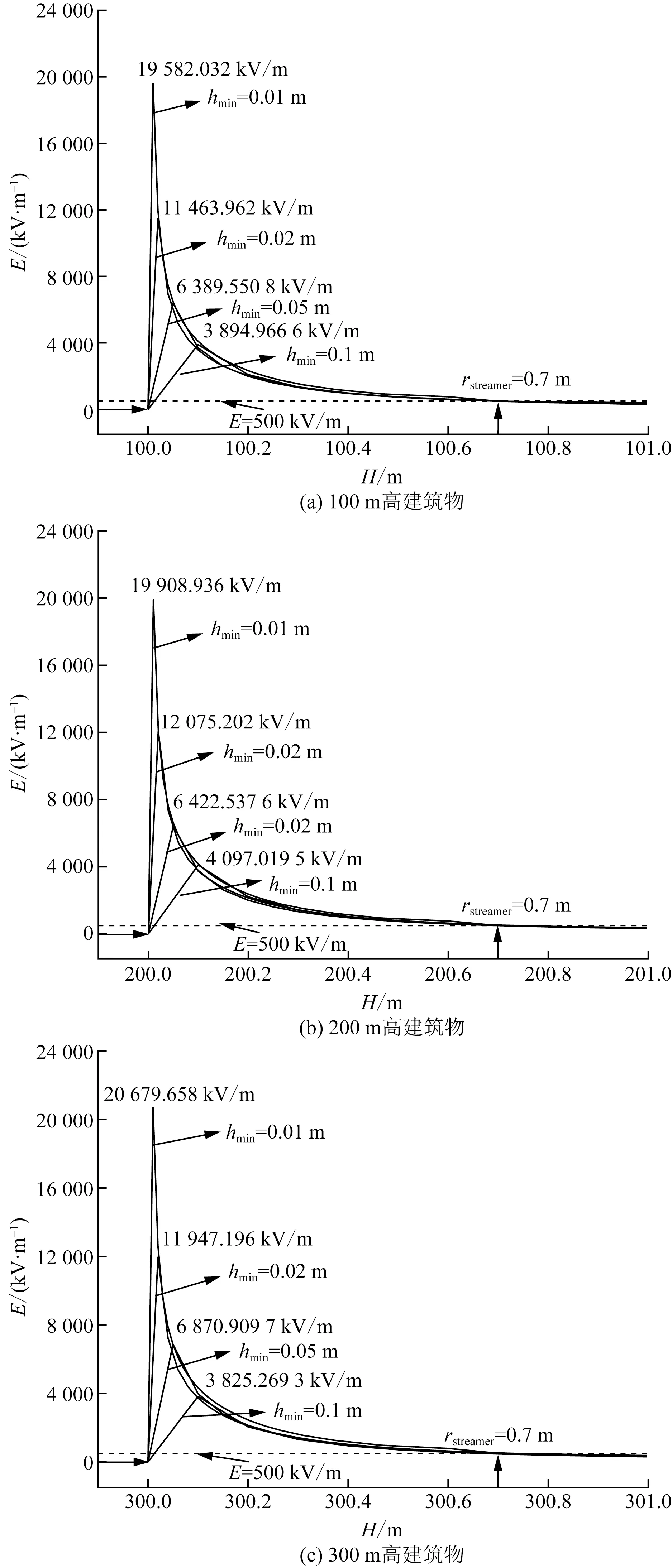
E为电场强度；rstreamer为流光区长度；hmin为空间分辨率；H为高度

按照Petrov的临界长度法准则，用本文所建模型，将不同空间分辨率下在0.7 m处达到500 kV/m的电场强度所需要的背景电场值计算出来，如图5所示。由图5中曲线可知0.01 m的空间分辨率达到先导起始时所需要的背景电场值最大，随着空间分辨率的增大，所需的背景电场值逐渐变小。100、200、300 m建筑物高度下0.01 m与0.1 m的空间分辨率所需先导起始的背景电场值相差分别约为4.96、2.4、1.46 kV/m。4个空间分辨率的平均背景电场值分别是22.31、11.7、7.93 kV/m。

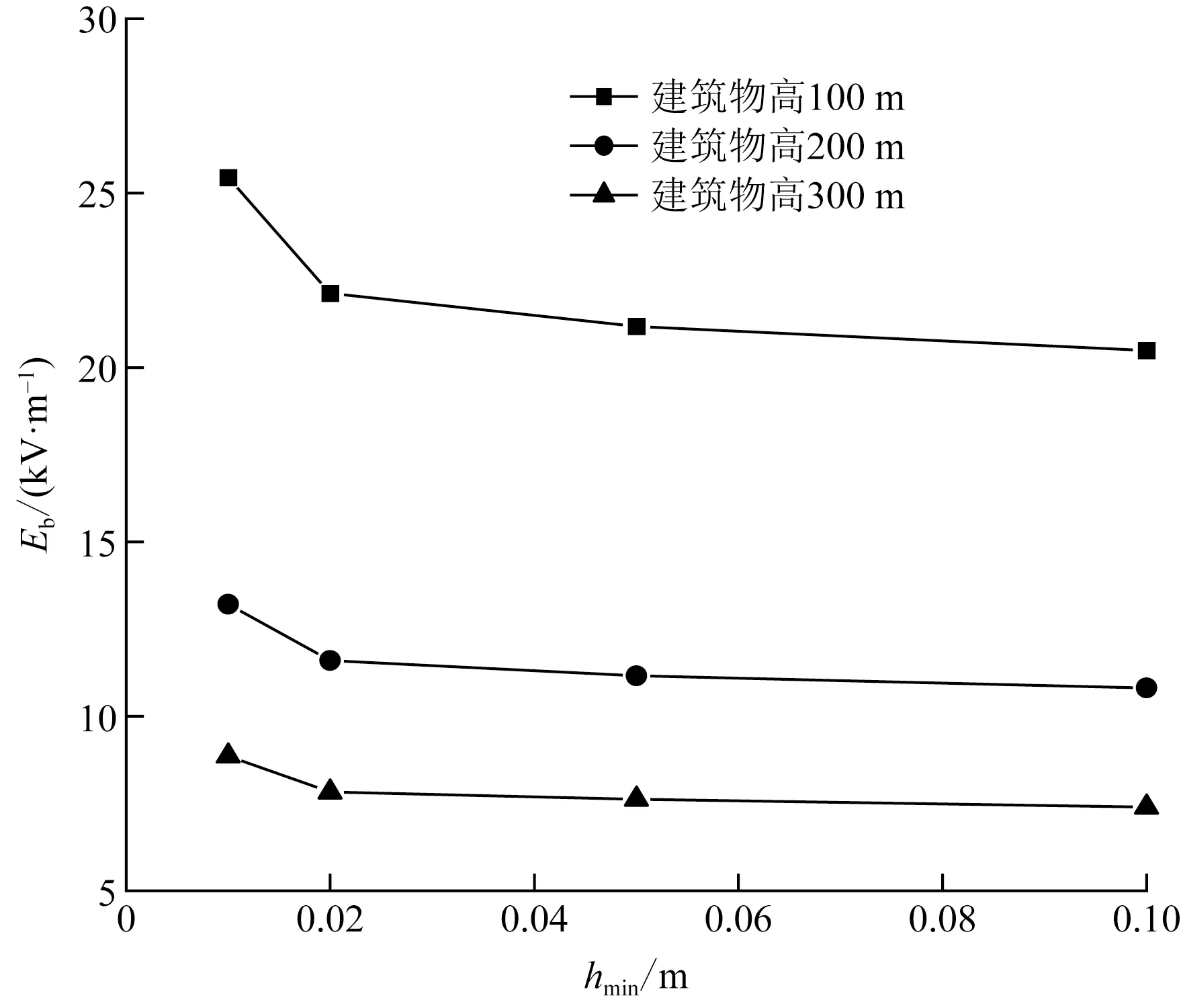
Eb为背景电场值；hmin为空间分辨率

假设0.01 m分辨率下计算出的环境电场值最接近现实结果，将另外几个分辨率下计算出的环境电场值除以0.01 m分辨率下的环境电场值，进行数据归一化处理。图6为3种不同建筑物高度在不同空间分辨率下计算出来的先导起始时环境电场结果的归一化计算结果，由图6中曲线可以看出在这3种建筑物高度模型中分辨率对Petrov的判据影响都不大。

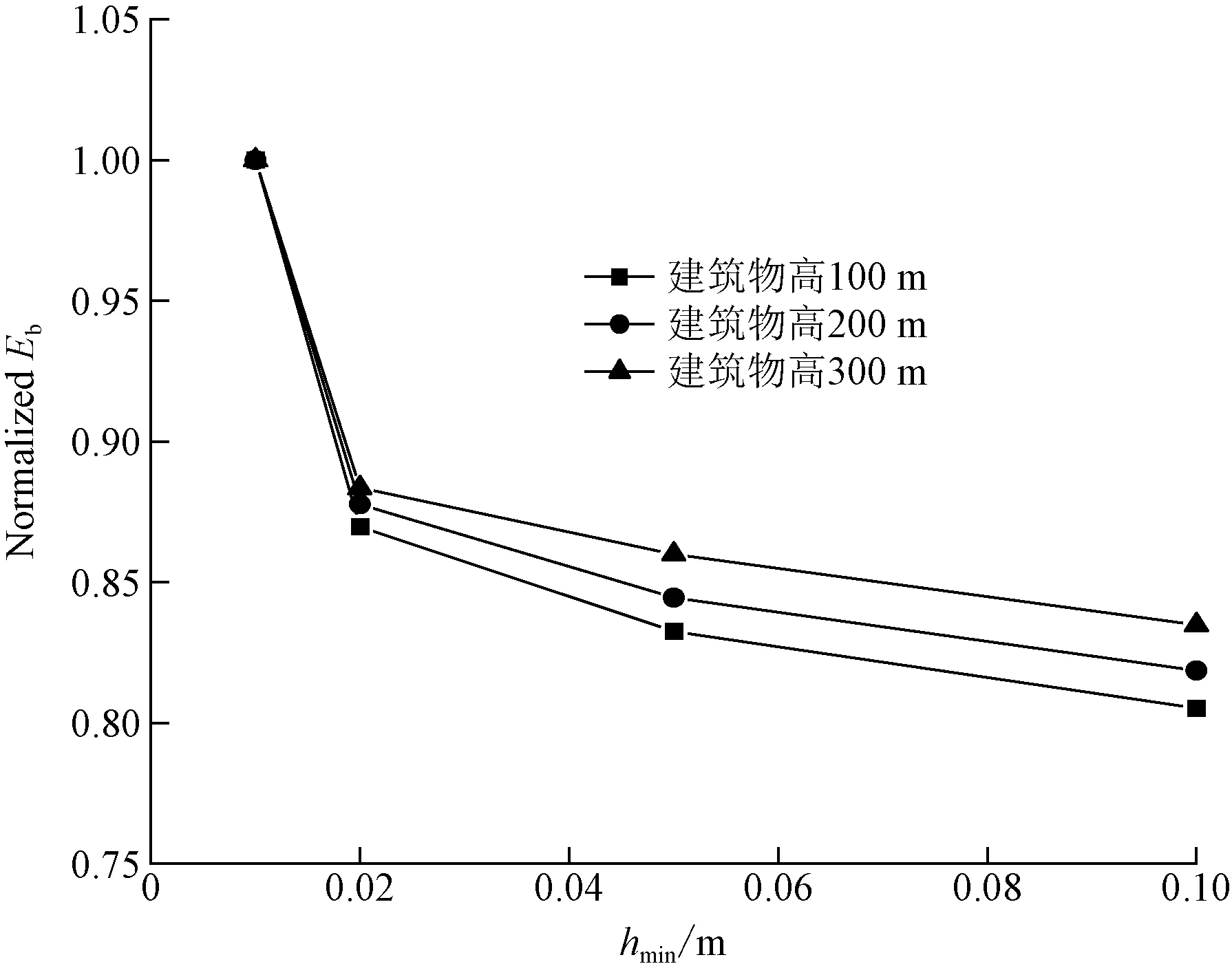
Normalized Eb为电场归一化后的值；hmin为空间分辨率

2.3 Becerra-Cooray上行先导自持始发模型

Gallimberti[25-26]建立了针对正极性先导的热动力学模型，计算得到正极性先导起始所需的临界电荷量约为1 μC。随后，Petrov[10]在Gallimberti[25-26]建立的针对正极性先导的热动力学模型的基础上，考虑了二次起晕过程，对正先导热力学模型进行了简化和推广。得出当流光向不稳定先导转换发生在背景电势分布高到足够产生相当于或高于1 μC的电晕电荷且当不稳定的先导持续传播长度达到2 m时，产生稳定的先导。

为了比较不同空间分辨率对该判据的影响，在基于有限差分法求解电场的程序基础上，按照Beccera的自持上行先导始发模型建立了先导始发模型程序。

图7为简化的几何近似法计算起始过程中电晕电荷量示意图。

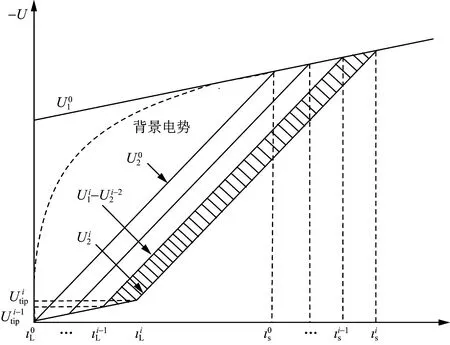
U为电势；Utip为先导头部电势；U1为背景电势；U2为初始电晕形成后的电势分布；lL为先导长度；ls为流光长度；i为先导发展步伐

(3)

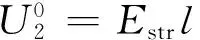
(4)

通过式(3)和式(4)可以得到电晕流光区前部的具体位置ls，m；且可以通过式(5)来表示：

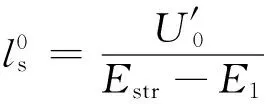
(5)

同时，可以结合式(4)和式(5)得到二次起晕的电荷量ΔQ0，C/V。计算公式为

(6)

式(6)中：KQ为几何参数，在简化模型中采用3.5×10-11C/(V·m)的值。

(7)

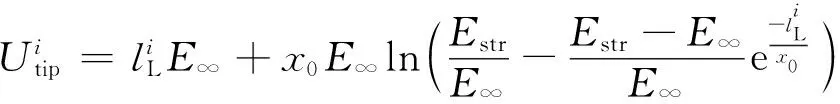
(8)

式(8)中：E∞为稳定状态下正极性先导电位梯度，约为3×104V/m；x0为常量参数，由正极性先导速度v(约1.5×104m/s)和时间常量θ(约50×10-6s)相乘得到，m。在第i步时，先导头部产生的电晕电荷量为

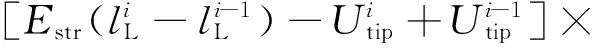
(9)

于是正极性先导以及头部电晕区向前发展的距离为

(10)

(11)

按照背景电场值在10 s内从0 kV/m发展到20 kV/m的增长率，计算出不同建筑物高度在不同空间分辨率下不稳定先导始发和稳定先导发展时所需的背景电场值，如图8 所示。

图8(a)为不稳定先导起始时所需的背景电场值，图8(b)为稳定先导起始时所需的背景电场值。两幅图中不同建筑物高度起始所需环境电场值的曲线趋势相同，0.01 m空间分辨率下先导起始所需的背景电场最小，随着空间分辨率的增大先导起始所需的背景电场值逐渐增大。100、200、300 m建筑物高度模型中0.01 m和0.1 m的空间分辨率下不稳定先导起始所需的背景电场值相差分别为0.282、0.18、0.148 kV/m，而稳定先导起始所需背景电场值相差分别为1.888、1.392、1.204 kV/m。不同空间分辨率带来的误差不大，不稳定先导起始平均背景电场分别为3.21、1.663 5、1.124 kV/m。稳定先导起始平均电场分别为36.104、19.248、13.143 kV/m。

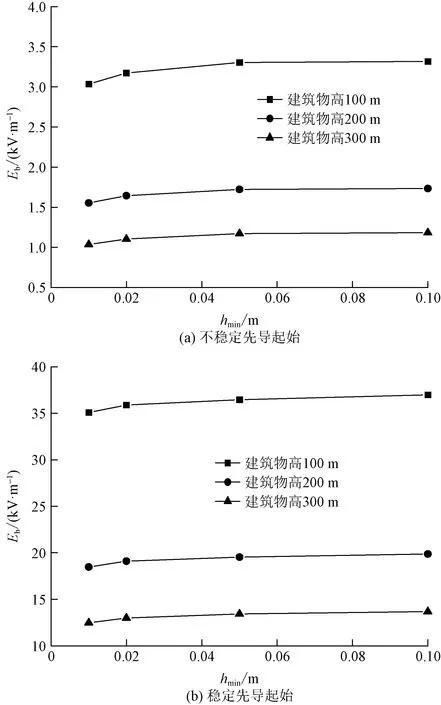
E为电场强度；hmin为空间分辨率

图9为三种不同建筑物高度在不同空间分辨率下计算出来的先导起始时环境电场结果的归一化计算结果。由图9中曲线可以看出，在这三种建筑物高度模型中分辨率对becerra的判据影响都不大。

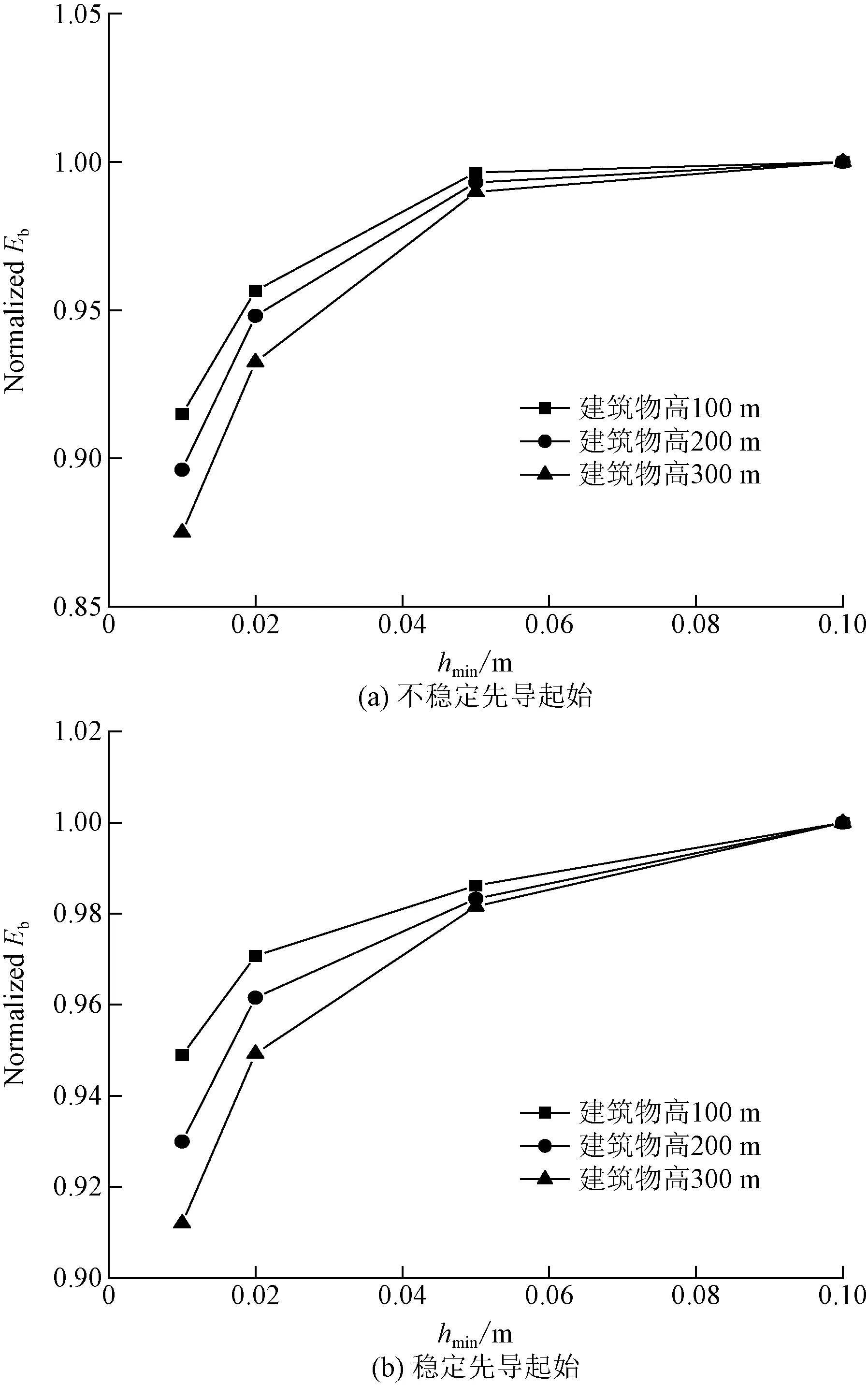
Normalized Eb为电场归一化后的值；hmin为空间分辨率

通过研究可知，Petrov的临界长度法和becerra的临界准则法受分辨率影响较小。对于研究先导速度、电流大小等数值模拟研究使用becerra的判据，对于研究上行先导传播分形等数值模拟研究使用Petrov的判据即可。

3 结论与讨论

通过对建立的长、宽为0.2、0.2 m，高分别为100、200、300 m的建筑物尖端进行数值模拟研究，得出如下结论。

(1)针对以表面电场为判据的先导始发模型，空间分辨率带来的影响较大，在使用此类判据时，可以通过拟合修正系数的方法来减小误差。

(2)针对一定区域内的电场或电势作为判据时，只要空间分辨率小于判定范围尺寸则不会对判定结果带来较大影响。

综上所述，当仅以表面电场作为判据时，空间分辨率带来的影响巨大；但当以一定区域内的电场或电势作为判据，则发现空间分辨率所带来的影响相对较小，几乎可以忽略。因此，在实际的模拟中，针对不同的判据，需不同对待，不只是提高分辨率。为了节省计算机的计算耗时，根据所要研究的内容，选取合适的先导始发判据，进而选择能表征尖端大小和判据中出现的尺寸范围的网格即可。此外，本文研究尚未考虑其他尺寸建筑物尖端始发上行先导时的情况，在后续工作中将对此进行研究。