轮毂电机电动汽车轮内悬置系统设计与优化

任洪卓，陈双，张宇涵

(辽宁工业大学汽车与交通工程学院，锦州 121000)

由于能源紧张、油价波动、环境污染和政治需求等原因，政府、汽车制造商开始考虑改变车辆的动力系统，电动汽车就此吸引了人们的目光并受到各个国家的高度重视[1]。与集中电机相比，采用轮毂电机直接驱动的电动汽车因具备更好的空间利用率、噪声(noise)、振动(vibration)与声振粗糙度(harshness)、安全性以及更简化的底盘结构引起了广大学者的高度关注和研究[2]。文献[3-4]对引入轮毂电机的电动汽车非簧载质量增加问题进行了研究分析，结果证明非簧载质量将会恶化整车的平顺性和安全性。但随着中国相关技术的快速发展，轮毂电机驱动的电动汽车拥有巨大的市场前景。

目前对轮毂电机相关技术的研发与使用还不够深入，针对其平顺性较集中电机驱动电动汽车有所恶化的问题，中外企业及学者进行了大量研究。文献[5]通过在电动轮内安装了一套螺旋弹簧-阻尼器的减振系统，使电机质量转化为吸振器，改善车辆的垂向负效应，缺点是结构过于复杂，有一定的局限性。文献[6]提出了车身减振、车轮减振、综合减振3种不同类型的减振系统，并利用粒子群算法优化减振系统参数。文献[7-8]在轮内设置了橡胶衬套，可以在一定程度上改善车辆的平顺性，但前者衬套数量不够，效果不够明显；后者没有对衬套参数进行有效的优化。文献[9]在设置轮内减振系统的基础上，提出将原车悬架改为半主动悬架，并设计了一种混合控制策略来优化汽车的平顺性。文献[10]介绍了一种新型轮毂电机聚磁式轴向磁通电机，不足之处在于此项技术并没有开发完善。

基于此，现以自主研发的可实现四轮独立驱动的轮毂电机电动汽车为实验对象，以优化汽车的平顺性和乘坐舒适性为目标，设计一种可安装于电动轮内的悬置系统，使电机的定子和转子分别与车轮结构实现弹性分离。考虑到电动轮内极度复杂、空间狭小且集成度较高的特点，选取橡胶衬套作为悬置系统的主要结构，并建立无悬置系统的整车七自由度模型、装备悬置系统的整车十一自由度模型以及四轮随机输入的路面模型，利用遗传算法对悬置系统橡胶衬套的刚度和阻尼值进行优化，确定其最佳值。最后通过在MATLAB环境中仿真对比有无悬置系统的车辆垂向振动特性，并进行实车实验，对此套悬置系统的应用性及有效性进行验证。

1 电动轮内悬置系统结构设计

目前主流的电动轮系统包括两种形式：一种是结构为内转子外定子型轮毂电机的电动车轮系统，此种驱动系统需要在轮内安装一套减速机构来配合运行；另一种结构则是内定子外转子型轮毂电机的电动车轮系统。本文研究中自主研发的电动汽车驱动形式为第二种，其轮内结构如图1所示。图1中的电动轮主要包含轮毂电机、制动系统、轮毂、轮辋和轮胎等结构，并且在定子上设计有油道来连接电机内外的冷却系统，有效实现电机的散热。

图1 轮毂电机驱动电动汽车轮内结构图

为了衰减振动、优化垂向特性，提出在电动轮内布置一套由橡胶衬套组成的悬置系统，目的是使电机质量与其他簧下质量实现弹性隔离，使整车增加了4个自由度。考虑到车辆行驶过程中，定子固定不动，转子同车轮共同转动，故本文将橡胶衬套分为三组：一组放置于电机定子和支承轴之间；二组放置于电机定子和悬架臂之间；三组放置于电机转子与轮辋之间。此三组橡胶衬套可根据实际情况酌情添加。一方面，此设计可将部分的非簧载质量与车身变相并联，另一方面橡胶衬套可以吸收一部分路面激励传递到电动轮内部的振动，以此减少对电机的不利影响，优化车辆垂向特性。图2为轮内悬置系统结构原理图。

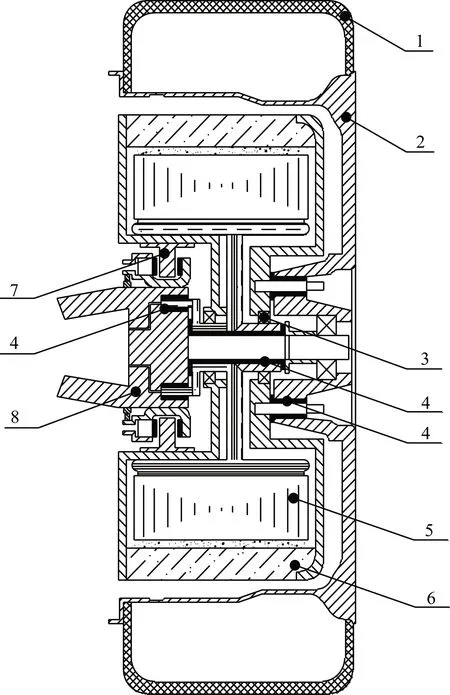
1为轮胎；2为轮辋；3为轴承；4为橡胶衬套；5为定子；6为转子；7为制动器；8为悬架臂

2 整车动力学模型及路面模型建立

车辆模型是研究车辆悬架性能的基础，从理论层面来讲，车辆模型中考虑的自由度越多就越能够反映出汽车的实际情况，仿真结果也就会越准确。因此，为了能够完整地反映出车辆车身状态即俯仰、侧倾等运动的变化，分别建立了轮毂电机驱动的电动汽车整车七自由度模型、具备悬置系统的整车十一自由度模型及四轮随机输入路面模型，为后续悬置系统参数的匹配及优化奠定基础。

2.1 整车动力学模型的建立

为了体现内置悬置系统对车辆振动特性的影响，分别建立有、无内置悬置系统的整车十一自由度模型和七自由度模型。七自由度分别为车身垂向运动、俯仰运动、侧倾运动及4个车轮的垂向运动。

十一自由度增加了4个电机的垂向运动。模型假设条件如下。

(1)车身和车轮均为独立的刚体，二者的垂向运动不存在相互影响的情况。

(2)不考虑橡胶材质的轮胎所具有的阻尼值，将轮胎视为具备相同垂向刚度的弹簧，轮胎在所有工况下都保持在地面滚动的状态。根据上述条件建立如图3所示的模型。

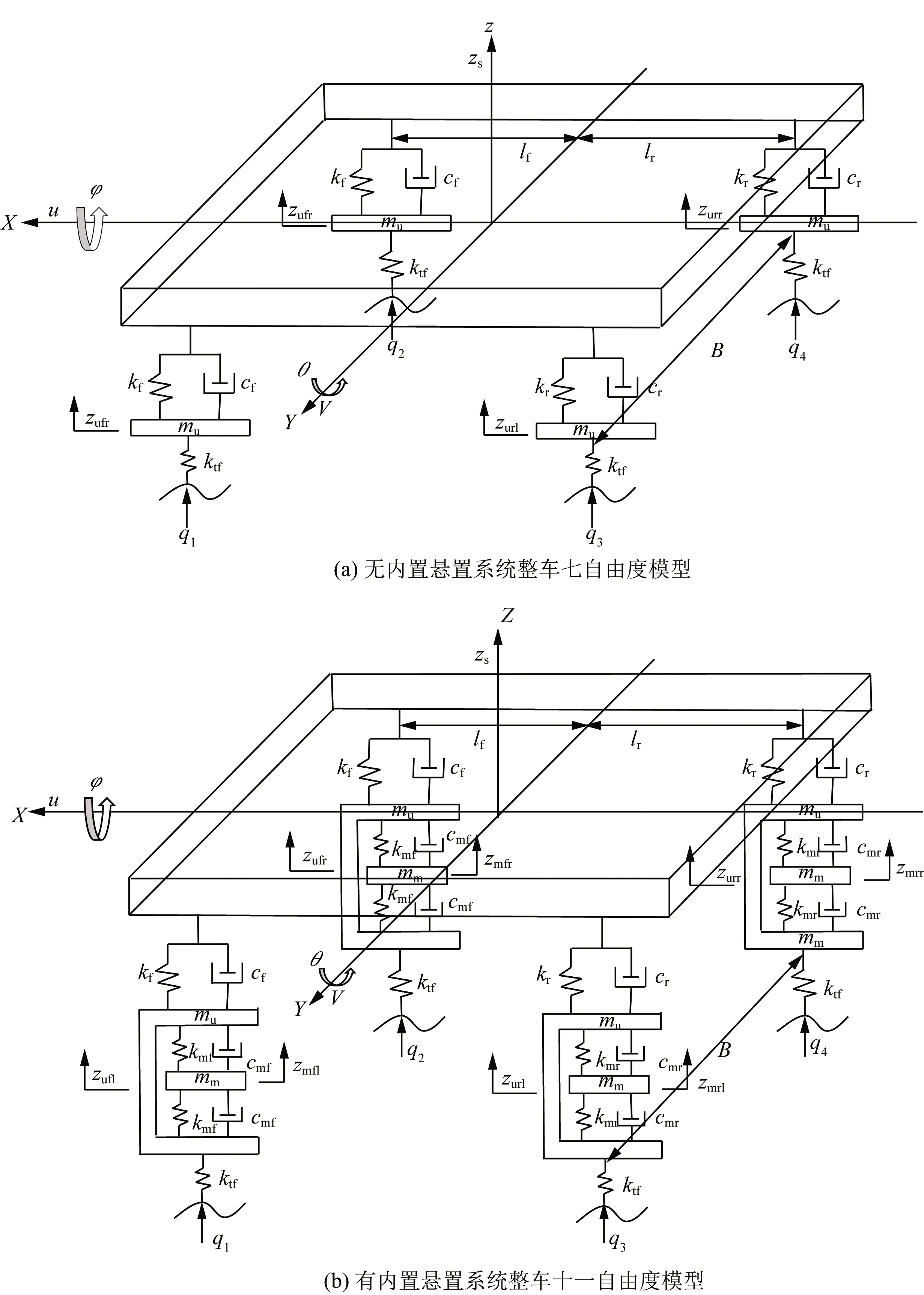
kf为前悬架弹簧刚度，N/m；kr为后悬架弹簧刚度，N/m；ktf为轮胎刚度，N/m；cf为前悬架阻尼系数，(N·s)/m；cr为后悬架阻尼系数，(N·s)/m；kmf为前悬置系统刚度，N/m；kmr为后悬置系统刚度，N/m；cmf为前悬置系统阻尼系数，(N·s)/m；cmr为后悬置系统阻尼系数，(N·s)/m；lf为前轴至质心距离，m；lr为后轴至质心距离，m；B为轮距，m；θ为车身俯仰角，rad；φ为车身侧倾角，rad；zufl、zufr、zurl、zurr为左前轮、右前轮、左后轮、右后轮垂向位移，m；zmfl、zmfr、zmrl、zmrr为左前、右前、左后、右后电机的垂向位移，m；。u为纵向车速，m/s；V为横向速度，单位m/s；ms为车身质量，kg；mt为整车质量，kg；mm为电机质量，kg；mu为轮胎质量，kg；qi为路面激励(i=1,2,3,4)，m

根据所定义的坐标系，微分方程为

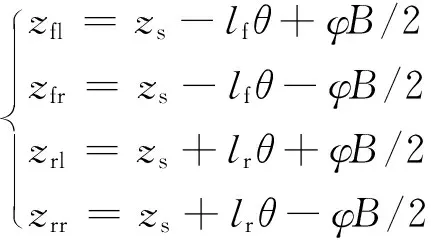
(1)

式(1)中：zs为车身垂向位移，m；zfl、zfr、zrl、zrr分别为左前车身、右前车身、左后车身、右后车身垂向位移，m。

对于整车七自由度动力学模型，车身垂向运动方程为

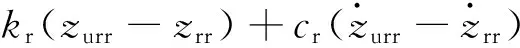
(2)

车身俯仰运动方程为

(3)

车身侧倾运动方程为

(4)

4个车轮垂向运动方程为

(5)

整车十一自由度动力学模型只列出变化的4个电机和4个车轮的垂向运动，其他不变。

4个电机垂向运动方程为

(6)

4个车轮垂向运动方程为

(7)

通过式(1)～式(7)，在MATLAB/Simulink中分别建立出四轮随机输入路面模型、七自由度无悬置系统整车动力学模型以及十一自由度悬置系统整车动力学模型，为后文对比有无悬置系统的汽车平顺性评价指标奠定基础。

2.2 四轮随机输入路面模型的建立

汽车在路面上直线行驶时，前后轮具有相同的路面输入，不同之处在于后轮的输入时间要延后一些，在车速不变的情况下，延后时间为轴距与车速之比。

除此之外，在车辆建模的过程中还考虑到了左右两侧车轮互相影响的问题。据此，可用式(8)～式(10)表示出四轮随机输入路面模型。

(8)

Y(t)=[q1(t)q2(t)q3(t)q4(t)x1(t)x2(t)]

(9)

(10)

(11)

(12)

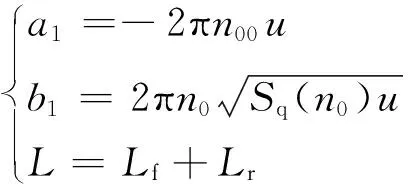
(13)

式中：Sq(n0)为路面不平度系数，m3；n00为空间截止频率，m-1；n0为标准空间频率，m-1。

3 电动轮内悬置系统参数优化

3.1 遗传算法介绍

由于整套悬置系统的引入，使实验车的悬架系统结构发生了很大程度的改变，由微分方程可知，车辆力学参数、质量参数和几何参数同平顺性之间具有极其复杂的非线性关系，正是这些参数的选择影响汽车的平顺性，排除掉车辆本身的固有悬架参数不变，对悬置系统橡胶衬套的刚度和阻尼值进行优化就显得极其有必要。因此选取前后悬架悬置系统内的橡胶衬套的刚度和阻尼作为优化目标，采用遗传算法，在MATLAB环境内进行操作。

遗传算法隶属于统计理论，它的基本原理是物竞天择、适者生存、遗传继承，经过一系列的组合优化、搜索得出最优解。遗传算法的应用范围比较广泛，在科学社会、人工智能、控制领域都能看到它的身影，具有不可替代的功能。遗传算法在优化过程中，主要通过选择、交叉、变异3个步骤完成目标优化。

(1)选择操作：其主要目标是把生成的种群中适应度较好，生命力强的个体挑选出来，经过繁殖产生下一代新的种群。

(2)交叉操作：随机选择种群中的两个个体，交换他们的基因，从而形成新的个体。

(3)变异操作：模拟人类染色体变异的行为，将某些个体的某些基因由其等位基因来代替。

此外，遗传算法在设计过程中还有编码、生成种群、适应度及目标函数的设计、解码等流程，在此不一一解释。

3.2 参数优化

本文研究的最终目标是优化轮毂电机驱动汽车的行驶平顺性，考虑到评价平顺性的指标主要为车身加速度，再综合考虑到轮胎动载荷对轮胎的接地性有一定的影响从而影响车辆的安全性，据此确定了目标函数的形式，j为目标函数具体值。同时应该保证悬架动行程在2 cm以内，以防止撞击到限位块，并以此确定了约束条件。目标函数为

(14)

约束条件为

l<0.02

(15)

式中：RMS为均方根值；a1为悬置系统簧载质量(车身)加速度；a2为无悬置系统簧载质量(车身)加速度；F1为悬置系统轮胎动载荷；F2为无悬置系统轮胎动载荷；l为悬架动行程。

目标函数和约束条件确定后，对基于橡胶衬套的轮内减振系统的刚度和阻尼值进行遗传算法优化，选取种群数量为40，遗传代数80代为终止条件，变异概率为0.3，交叉概率为0.95，优化过程如图4所示。

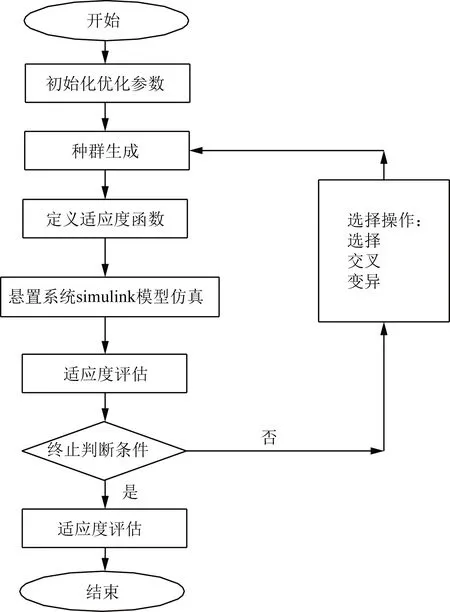
图4 遗传算法优化图

使用编写的遗传算法程序，在MATLAB和Simulink环境中进行联合仿真优化，当进化到50代时目标函数值最小为0.954 721，且在50代之后目标函数值保持不变。故得出此时为最优解，遗传算法进化过程如图5所示，具体结果为：kmf=11 765 N/m，cmf=11(N·s)/m，kmr=13 290 N/m，cmr=1 263(N·s)/m。

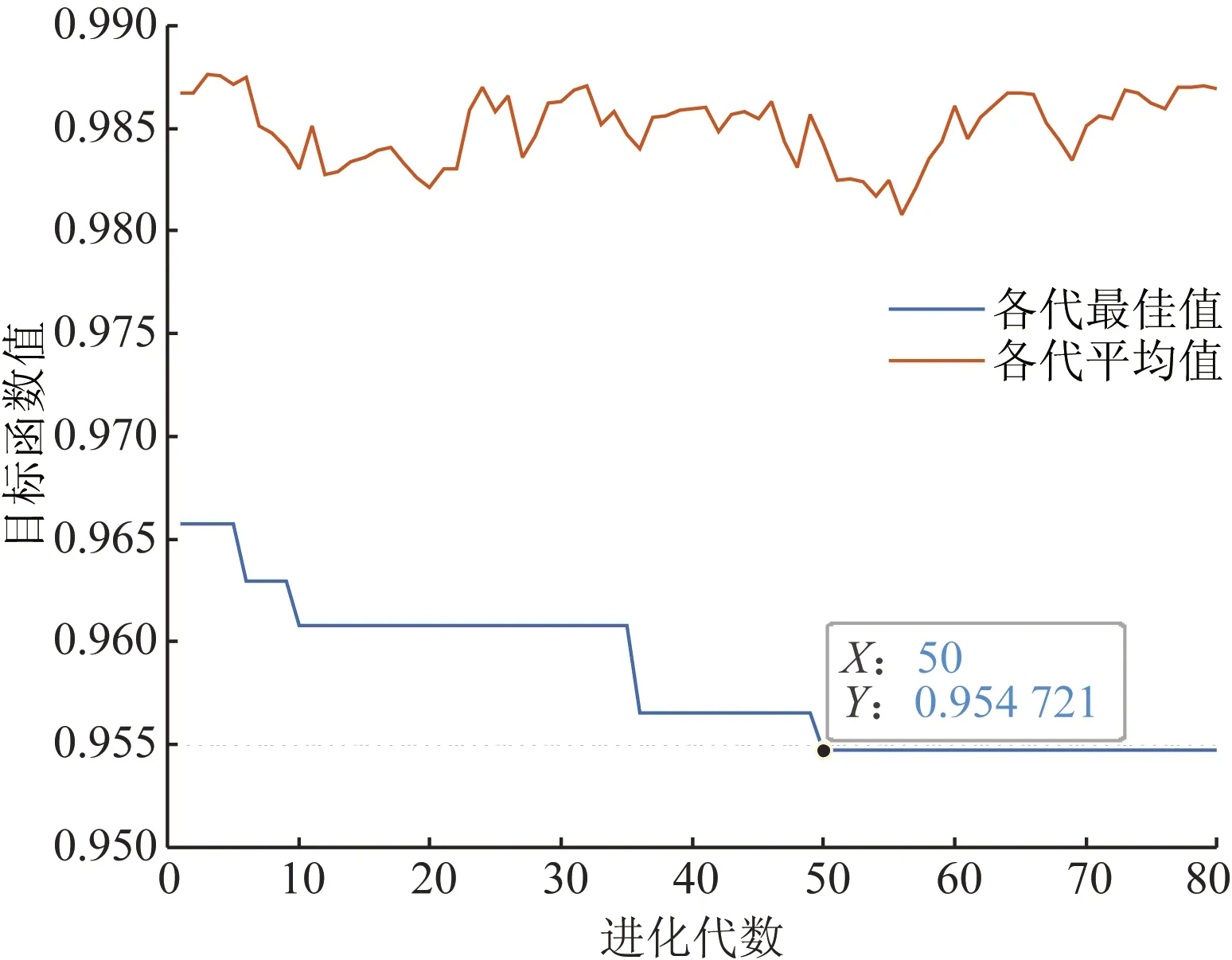
图5 遗传算法进化图

4 汽车平顺性仿真分析

4.1 仿真工况

路面模型选取为乘用车最常行驶的B级路面，设定其路面不平度系数Sq(n0)=64×10-6m3, 空间截止频率为n00=0.01 m-1，标准空间频率n0=0.1 m-1,车速为70 km/h，在MATLAB/Simulink中建立的四轮相关路面随机激励如图6所示。自主研发的电动汽车具体参数如表1所示。

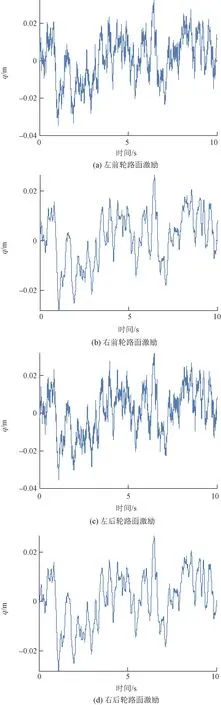
q为路面激励

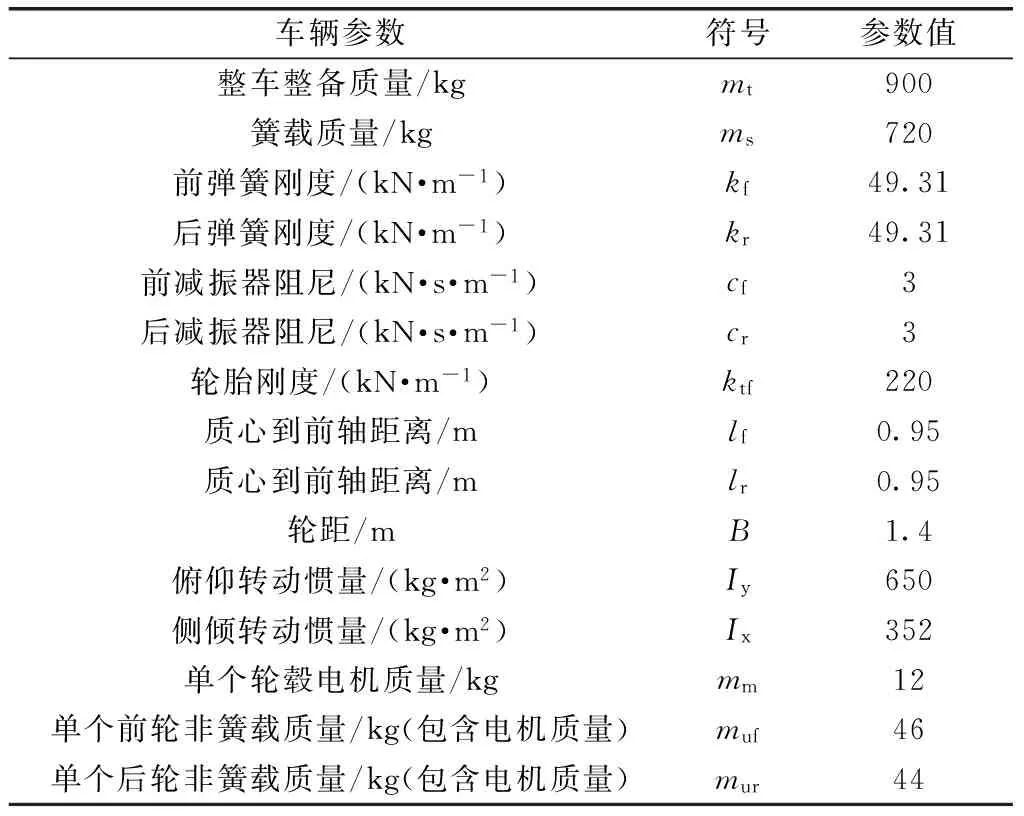
表1 车辆参数表

4.2 仿真分析结果

在MATLAB环境下对模型进行平顺性仿真分析，评价指标仿真曲线对比结果如图7所示。可以看出，在车身加速度时域曲线中，悬置系统对于车身加速度有明显优化，各个点位的峰值均有所降低；车身加速度的频域曲线可以看出悬置系统对于中频段的振动优化效果较好，其他频率只有个别点位有优化效果。由轮胎动荷载的时域曲线可分析出，悬置系统对车辆前轮的轮胎动载荷有一定的优化效果，但没有对车身加速度的优化效果好，时域图中看不出对后轮有明显优化；轮胎动载荷的频域图可以看出，悬置系统的引入使前轮中频阶段的动载荷有所减小，高频和低频阶段基本持平，对于后轮的优化不太明显。

图7 平顺性评价指标对比图

车身加速度和4个车轮的轮胎动载荷均方根值对比结果如表2所示，可以看出，悬置系统的引入对车身加速度的优化效果比较明显，车身加速度优化7.72%，左前轮优化4.8%，右前轮优化2.8%，左后轮优化1.58%，右后轮优化0.56%。

表2 均方根值对比结果

5 悬置系统实车实验

为了验证所设计的悬置系统在实际应用中的可靠性与有效性，加工制造了轮内悬置系统实物并成功安装于自主研发的轮毂电机驱动电动汽车上进行实车实验。由于受实验条件限制，布置于电机内的两组橡胶衬套暂时无法顺利安装，因此，只在电机与轮辋连接处设置了一组橡胶衬套，验证轮内悬置系统其车辆平顺性的优化作用。由于车辆平顺性的主要评价指标为车身垂向加速度，车轮动载荷主要影响轮胎的接地性能进而影响操纵稳定性，因此，只对车身的垂向加速度进行实验分析。

实车验证过程分为两步：①悬置系统实物设计与安装；②轮毂电机电动汽车平顺性实验及无、有悬置系统性能对比分析。对悬置系统实物进行设计过程中，首先需要对原车的轮毂螺栓孔进行扩孔操作，留出空间用以布置橡胶构成轮内悬置系统，如图8所示。原轮毂的螺栓孔直径为15 mm，扩孔后为24 mm。

图8 扩孔加工方案

通过定制模具、选择合适的胶种，调整橡胶浓度等方法，加工出与前文遗传算法优化所得出的最佳刚度和阻尼系数基本一致的橡胶衬套。具体尺寸为长13 mm，外径23.6 mm，内径12.4 mm，如图9所示。具体刚度和阻尼系数分别为：kmf=12 000 N/m，cmf=100(N·s)/m，kmr=13 000 N/m，cmf=1 300(N·s)/m。

图9 模具及橡胶衬套

悬置系统的安装及有无悬置系统的结构对比如图10所示。

图10 有、无悬置系统对比

实验过程中选取行驶车速v=10、25、40 km/h进行3次实验，如图11所示。实验数据采集利用车速传感器与陀螺仪，借助ARMS软件获取不同车速下的车身垂向加速度，经过数据处理后获得的时域曲线如图12所示。由于实验环节只设置了一套悬置系统，且实验路面与仿真路面并不相同，因此，仅根据车身垂向加速度的时域曲线以及均方根值、最值来评价悬置系统对车辆平顺性的优化效果，不与仿真结果进行对比分析。结果对比如表3所示。

图11 平顺性实验

由表3和图12以看出，悬置系统的引入对于车身垂向振动负效应有较好的抑制效果，3种不同车速下，车身垂向加速度的极值几乎都有大幅度的降低，只有40 km/h车速下的最大值有略微增加的趋势，且在整个时间历程内，可以明显地观察到装备悬置系统的车身加速度曲线波动要小于无悬置系统。在10、25、40 km/h 3种不同车速下，车身垂向加速度的均方根值分别降低了4.18%、5.8%、5.49%；最大值分别降低了18.59%、12.27%、-4.08%；最小值分别降低了33.81%、13.83%、11.92%。该实验环节有力的证明了悬置系统对于改善车身垂向加速度的有效性及可应用性。

表3 不同车速下有无悬置系统车身垂向加速度对比

图12 有无悬置系统车身垂向加速度

6 结论

以自主研发的轮毂电机驱动汽车为基础，设计了一套轮内悬置系统加装在轮毂电机与轮内其他结构之间，使电机在轮内处于被隔离状态。悬置系统的结构为橡胶衬套，通过遗传算法确定最佳的橡胶刚度和阻尼系数，实现了车身加速度一定程度的优化以及轮胎动载荷的小幅度优化，最后通过悬置系统的实车实验有力地证明了此系统对于抑制车身垂向振动负效应的有效性。此套悬置系统同时兼顾了系统的高度集成和优良的表现，对如何解决由于电机的引入导致轮毂电机驱动电动汽车平顺性和乘坐舒适性恶化的问题给出了相应的解决方案，对轮毂电机驱动汽车减振系统研究也有重要意义。