数据挖掘方法在汽油辛烷值损失计算中的应用

吴苹，钟仪华，雍雪，张茜

(西南石油大学理学院，成都 610500)

当今的燃料能源多种多样，对应不同的机器和设备，其使用的能源燃料各不相同。小型车辆燃烧汽油，其排放对大气环境存在重要影响。为了保护大气环境，汽油清洁化是当今一个重要问题，其重点[1]在于降低汽油中的硫、烯烃含量，同时要尽量保持其辛烷值即降低辛烷值的损失。因此如果能对辛烷值的损失进行较为精细的预测，并在实际汽油清洁化方案进行过程中加以配合使用，就可以尽早评估出清洁化方案的合理性，可以有效避免某些汽油清洁化方案的低效性，提高实际生产中清洁化的效率。

关于辛烷值的损失预测，关键在于变化的辛烷值的计算，通常是同一清洁化时间段前后辛烷值的差值，因此问题转化为对终端的辛烷值进行定量计算进而返回计算差值预测出辛烷值的损失。

目前，中外相关研究已从不同视角对辛烷值(research octane number，RON)的定量计算进行了合理的探索，如采用符合美国材料实验协会和美国联邦法案标准的辛烷值机检测计算[2]，但其缺点不少，如存在耗时长、操作复杂、价格高和检验用量大等。另外，由于汽油辛烷值与其组成成分有着密切的关联，进而通过汽油的自身组分及其相关信息进行计算，如分析汽油混合物的组分以及含量，其由气相色谱实现，然后分析与汽油辛烷值之间相关性来计算辛烷值。这个方法称为色谱法[3]。但是很多时候，通过汽油的自身组分及其相关信息进行计算的方法是在光谱、色谱等精密仪器的组分分析上实现，对仪器的要求较高。在实际应用中汽车数量众多，因此实现汽油清洁化的覆盖面广，但其实际清洁全覆盖只是借助辛烷值机和色谱仪等精密仪器难以在实际生活中实现，因此计算辛烷值损失即汽油辛烷值的定量计算一直是难点。

除了以上借助仪器进行定量计算外，还有部分研究通过分析理化指标，借助数学理论来实现汽油辛烷值的定量计算。其中韩志歧[4]探究了汽油理化指标与辛烷值之间的联系，进而借助数学与统计理论，构建了理化指标计算汽油辛烷值的回归方程，但存在一定的主观性，因为需要人工不断处理和比较来筛选方程每一种参数和模型的建立，而且该方法只能建立线性模型，这样得到的模型的精度不足，存在极大可能所得结果不是最优。除此另一类常用的线性模型偏最小二乘法(partial least squares，PLS)[3]也同样存在以上不足。近年来，随着中国石化企业实验室信息管理系统的建成，积累了质量数据并共享了一定的数据。因此，以现有数据库中的汽油理化指标数据集为基础，开始探索和采用一些非线性的建模方法[3]，进行辛烷值的定量计算，如人工神经网络(artificial neural networks，ANN)的方法[5]。

具体各组分的体积溶度输入ANN，输出各个对应的RON，通过大量实验可以得到精度较高的模型。如秦玉翠[6]以误差反向传播人工神经网络(back propagation neural network，BP)为基础, 对近红外光谱仪测定数据进行相关分析，如光谱吸光度与汽油辛烷值，然后计算得到了较小的误差，进一步说明ANN方法的可行性。另外也有研究用支持向量机回归法[3]，如朱晓等[7]应用有关方法，以分子结构为依据，构建基于烷烃马达法的辛烷值计算模型，然后采用留一法验证模型，实验表明其有较高的稳定性。这些研究工作说明了采用非线性的建模方法有利于进一步精确对辛烷值进行定量计算，进而精确对辛烷值的损失定量计算，有利于提高汽油清洁化的效率。

因此，基于以上的工作，现结合ANN等非线性建模方法的优点，利用数据挖掘方法[8]研究辛烷值损失的定量计算问题。针对前面所述的问题，在前人基础上，更关注从应用的角度获得高泛化度的模型，关键在把握常用的挖掘方法的理论和各自特点的条件下，选择正确的使用步骤；通过有效的数据处理，利用合理的算法进行特征选择；并从多种挖掘方法构建的模型中经过实验优选出最优模型。以某石化企业为例，对比研究支持向量机回归、BP神经网络、广义回归神经网络(generalized regression neural network，GRNN)、随机森林和K近邻回归这5种方法进行辛烷值损失的定量计算，以期寻找出最佳的计算辛烷值损失的挖掘方法。

1 数据挖掘方法

数据挖掘方法是一种数据驱动式的应用方法，即它不强求人们需要事先完全理解所需解决问题的所有背景和各类性质，如汽油清洁化降低硫含量、辛烷值的所有化学性质和变化规律等，而只需要一定量的背景知识；然后根据现有的数据，从对数据的分析和处理建立模型；最后结合实际对模型进行应用和分析，以解决实际问题。在汽油清洁化中降低辛烷值损失，即对辛烷值的损失进行较为精确的定量计算对应着数据挖掘方法的预测和回归任务。为提高数据挖掘方法在解决问题的效率，设计了以下数据挖掘方法的应用流程，如图1所示。

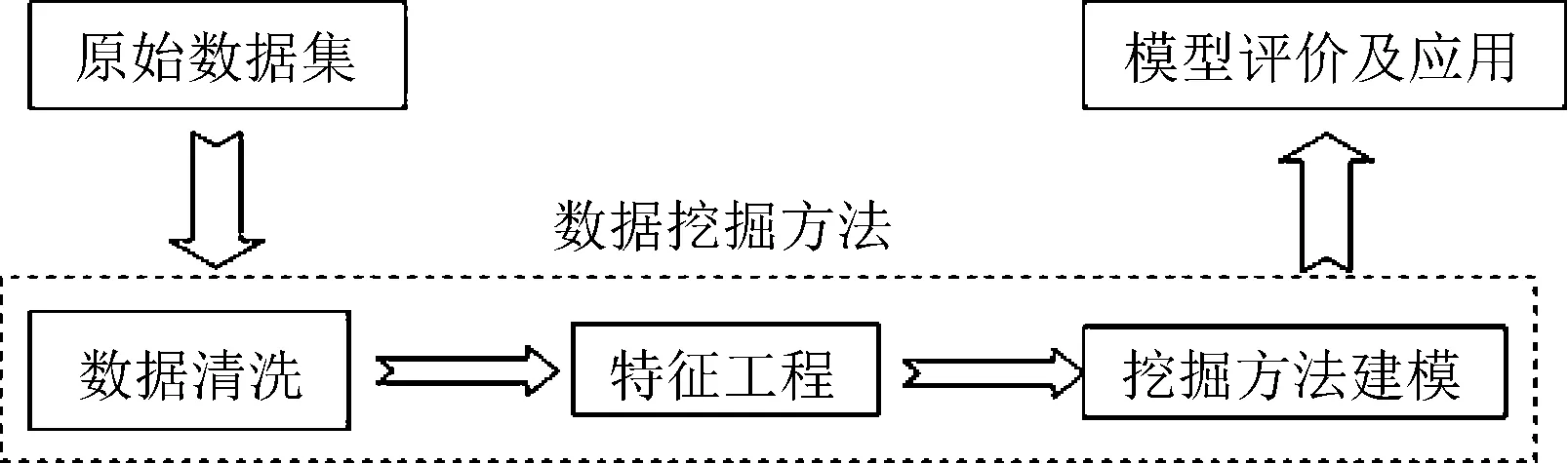
图1 数据挖掘方法流程

2 影响辛烷值损失的因素

在实际汽油清洁化中，影响辛烷值损失的因素很多，如包括原料性质、产品性质、待生吸附剂性质、再生吸附剂性质和操作变量这5个大类，其中原料性质即与其相关的化学性质，主要有硫含量、初始辛烷值和饱和烃。在工业上，饱和烃可分为烷烃、环烷烃、烯烃和芳烃等，待生吸附剂性质主要以焦炭为主。另外，结合实际工业生产，众多影响因素中操作变量占比较大，而且对辛烷值损失程度的影响[9]也很大。例如，①氢油比，它的增大会加快烯烃通过加氢饱和成烷烃的反应速率，进而加快辛烷值的损失；②吸附剂载硫量，如果它变低，会使得吸附剂活性会变高和烯烃会变大，然后通过加氢饱和成烷烃反应程度的方式来变大，这同样会使得辛烷值损失会变大；③反应温度，当其他操作条件基本不变时，温度的升高，使得汽油辛烷值损失会逐渐减少。

3 基于数据挖掘辛烷值损失计算方法

以某石化企业积累的数据为例，应用数据挖掘方法和辛烷值影响因素分析的结果，寻找出最佳的辛烷值损失的定量计算方法。

3.1 数据清洗

3.1.1 缺失值处理

如果某些特征属性的残缺数据较多，使得无法补充，就删除此类点。另外，直接删除样本中该因素全部为空值的点。对于数据只有部分存在空值的点，空值处用其前后数据的平均值进行插值替换。具体通过Python 3.7进行编程实现，并统计了所有特征属性缺失占其自身的缺失比例如图2和表1所示。表1中展示了前20个缺失比例较大的特征元素及其缺失所占比例。

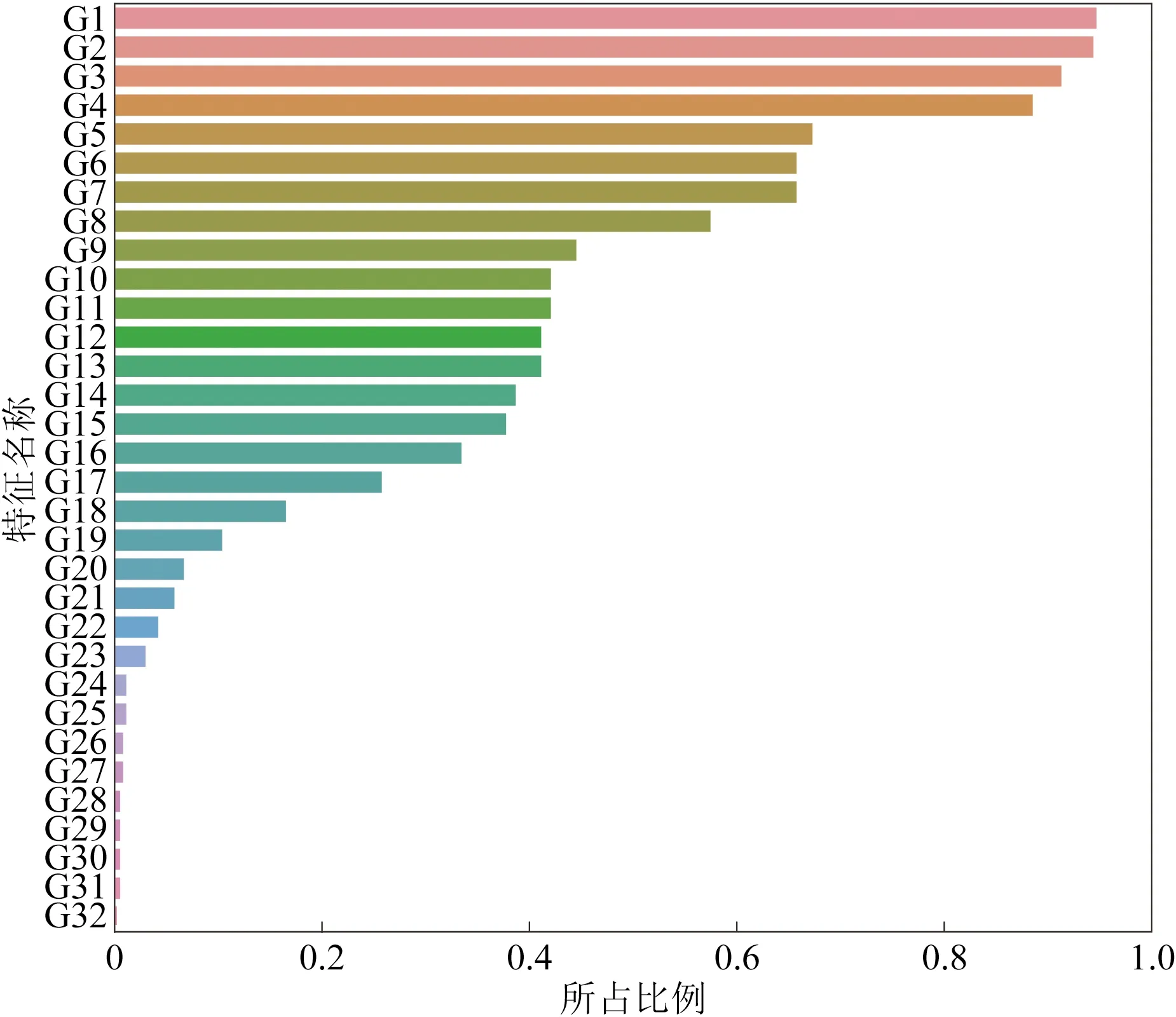
G1～G32为对应的特征元素

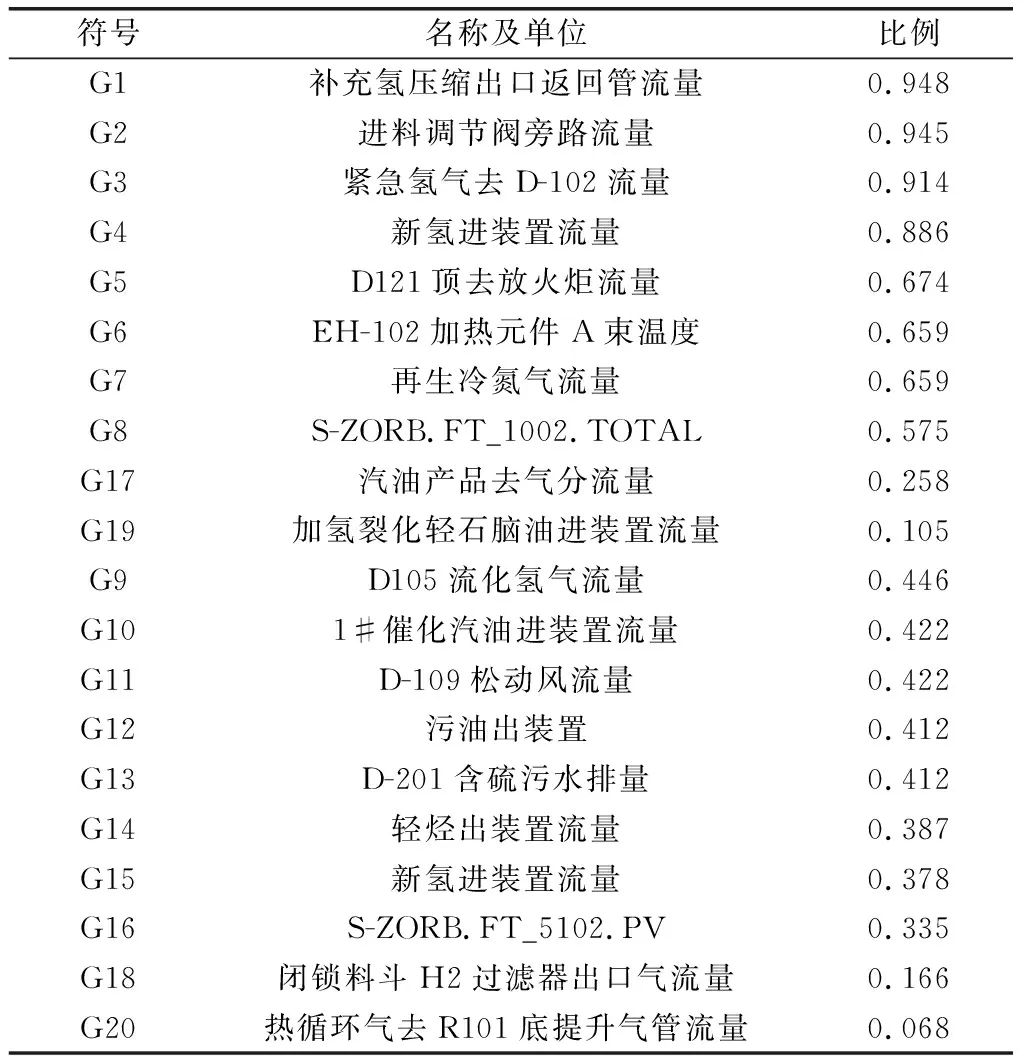
表1 前20个缺失比例较大的特征元素

由表1和图2可得缺失值占比较多的为补充氢压缩机出口返回管流量、进料调节阀旁路流量、紧急氢气去D-102流量和新氢进装置流量等，进行了删除；然后对比例较小如非净化风进装置流量以及D-123蒸汽出口流量等进行插值处理。

3.1.2 异常值处理

先根据企业的工艺要求与操作经验，获得影响因素的存在区间；然后对不在此区间的样本即异常值进行剔除；除此还根据拉依达准则进一步去除异常值，同样借助Python 3.7进行编程实现，并统计异常值较多的因素并作图如图3所示。由图3可得异常值较多的如催化汽油进装置总流量、精制汽油出装置硫含量和再生烟气氧含量等直接剔除。

H1～H8分别为精制汽油出装置硫含量、原料缓冲罐液位、再生烟气氧含量、新氢进装置流量、原料进装置流量累计、R-101床层中部温度、SZorbAT-0012号吸附和反应器料位

3.1.3 归一化

由于影响辛烷值损失的各个因素性质及其数据本身的含义存在差异，相互之间的量纲普遍存在差距过大，因此必须对数据进行归一化处理。为最大限度保留数据特性，对数据进行最常用的线性放缩法，具体公式为

(1)

式(1)中：xmin和xmax分别为该因素数据中的最大值和最小值，归一化到0～1。

3.2 特征工程

针对影响因素复杂繁多，对它们进行主要因素提取就十分必要。因为一般原始因素数据的特征和属性多样，具体表现为包含大量的干扰特征如噪音和冗余特征等，它们不但会影响构建模型的可靠度如产生过拟合，同时也会对模型应用有着一定的影响。主要特征的提取方法有很多，其中最常见的是主成分分析法，但它为线性方法，且一般这类方法得到的低维特征是其他高维特征通过线性组合而来，难以具有一定的物理解释与含义，不便于对辛烷值损失的主要因素的提取进行合理解释，故其并不适用于本文研究。

以某石化企业为例，其提供数据中影响辛烷值损失的因素有366个，因素较多且存在一定的干扰因素，故需提取出其主要因素。在查阅有关资料[10]，采用Wrapper方法类中的一种非线性方法即基于回归的随机森林的递归特征消除算法[11](ecursive feature elimination algorithm based on regression random forest，RFR-RFE)，提取主要影响因素的算法步骤如下。

假设数据集为T(X,Y)，其中X∈Rn×m，Y∈R，R为实数集，n为样本个数，m为因素个数，RFE算法最终提取结果为最优特征子集Best-T。

步骤1初始化，当前特征子集Current-T包含全部的因素，此时Best-T为空。

步骤2设定每次迭代需要删除的特征数量百分比，这里设为β%。

步骤3开始迭代，结束条件为Current-T为空，根据Current-T特征构建RFR模型，得到RFR特征重要性序列；移除当前特征子集Current-T重要性序列末尾的β%个特征。

步骤4将训练得到最优的RFR模型，若此时Current-T准确率大于Best-T，则令二者相等。

步骤5将Best-T的特征序列作为最终结果返回。

因此，在进行了数据清洗后，根据以上算法步骤提取出了28个辛烷值损失的主要影响因素(M1～M28)，并计算了主要因素之间相关系数，再根据所计算出的结果作出了相关性图，如图4所示。

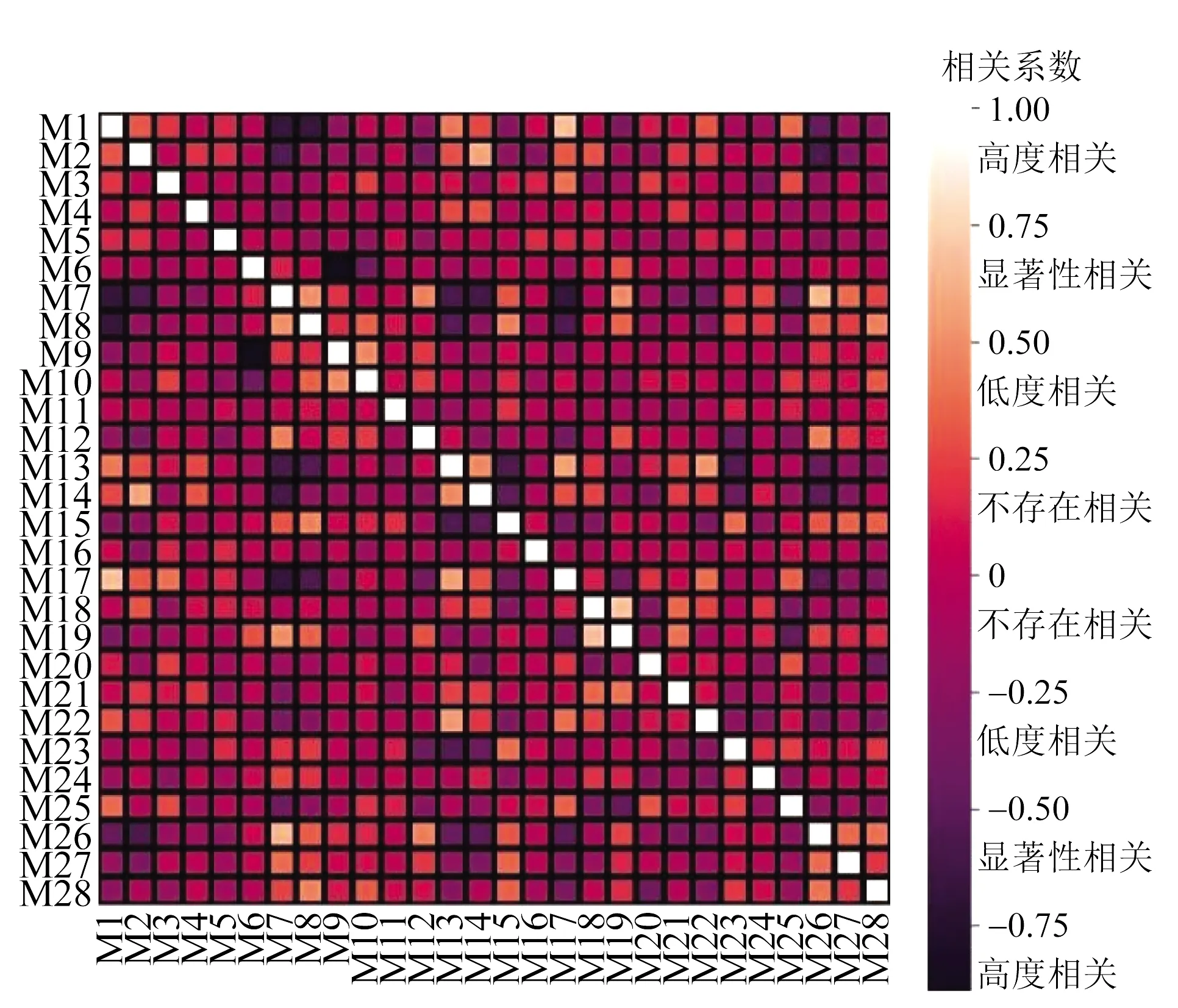
图4 主要因素间的相关性图

通过对比分析，发现28个特征相互之间的相关性大部分在0～0.4即相关性很低，进一步说明RFR-RFE方法的适用性和提取出的因素的合理性。最后，经过合理提取主要因素，影响辛烷值损失的主要因素M1～M28依次如表2所示。

表2 提取出的影响辛烷值损失的主要因素

3.3 基于数据挖掘的辛烷值损失预测模型

在对已有数据集进行数据清洗和特征工程即对影响辛烷值损失的主要因素进行提取后，下面应用数据挖掘方法构建计算辛烷值损失的模型，即先通过构建的模型进行辛烷值的定量计算，然后再进行辛烷值损失的计算。以数据挖掘常用的方法[9-10]为依据，结合辛烷值损失的主要因素和性质特点分析，得出传统的线性回归、逻辑回归等方法不适用于本文的建模。因为它们存在丢失信息量，而且文中的数据包含动态数据、具有较为复杂的内在结构，所以需要采用其他常用数据挖掘方法进行建模。

3.3.1 支持向量机回归模型

它是一种基于核方法的模型，依据其基本的原理[12]，结合本问题，找出一个映射函数，把原始低维空间的辛烷值损失的影响因素集映射到一个更高维的空间中去；然后非线性问题由此可以近似为一个线性问题，在高维空间中解决该问题。首先构造最优决策函数[12]为

f(x)=wΤK(xi,zi)+b

(2)

式(2)中：K(xi,zi)为核函数;对于辛烷值的损失而言;xi为其中某一个样本;zi为另一个样本;w为权重量;b为阈值。核函数即所找映射函数，它的正确选择对构建支持向量机回归模型的性能至关重要。高斯核函数由于参数较少和计算灵活，是非线性问题中最常用的，结合本问题特点选用高斯核函数，其表达式为

K(xi,zi)=e-γ‖xi-zi‖2

(3)

式(3)中：γ为伽马参数，其作用为调整高斯核的带宽。

根据文献资料[12]，在构建支持向量机回归模型时,可以同时最小化模型的复杂度, 并且通常可以收敛到一个局部最优解。以前面为基础，将其转化为拉格朗日函数, 其转换的方法为，利用对偶原理引入拉格朗日乘子和Karush-Kuhn-Tucker条件进行消参，进而可以得出计算辛烷值损失的支持向量机回归模型为

(4)

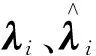
3.3.2 BP神经网络模型

它是目前应用最广泛的一种神经网络。将本问题结合其 BP神经网络结构计算过程如下：在正向传播时，输入影响辛烷值损失的因素从输入层进入隐含层，当其中一个神经元xi接收到来自上一个的计算值后，会通过权重wi传递的总输入和阈值进行比较，其中训练网络时会根据网络的计算误差且wi为各神经元相互间的权重，通过反向传播调整网络的权重wi和阈值θ，最后通过设定的激活函数计算出最终辛烷值损失值，其中一个重要表达式为

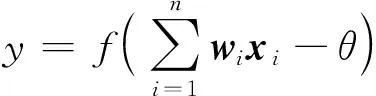
(5)

为得到更好地计算辛烷值损失模型，分别建立单隐层和多隐层的两种BP 网络进行计算。BP 网络参数设置对其计算结果有较大的影响，以赵煜等[13]和甄超等[14]的研究为基础，其中甄超等[14]指出通过试算法求得隐含层神经元个数且学习步长 lr 取值在0.01～0.2时，训练是平稳且收敛的；结合辛烷值损失问题和其主要因素的特点，本问题单隐含层节点数设置为8层，多隐含层网络层数依次设置为6和5，以及多次的网络训练，为防止过拟合采用提取停止法终止训练过程。最终，单隐含层网络的学习率lr设置为 0.2，目标误差0.000 4，训练次数500，设置tansig函数作为隐含层神经阈值函数，线性函数输出。多隐含层学习率 lr设置为 0.1，目标误差为0.000 1，训练次数400，其他与单隐含层设置类似，因而分别构建好预测辛烷值损失的单隐层和多隐层BP网络预测模型，分别简记为Single BP和Multiple BP。

3.3.3 GRNN神经网络模型

GRNN结构由输入层、模式层、求和层和输出层构成。另外，它的模式层和激活函数分别采用为径向神经元和径向基函数。它的基础是传统非线性回归且应用 Parzen非参数估计，并以最大概率原则通过求和层计算结果。在本问题中，以辛烷值损失的数据集为空间，其空间中每一点对应主要影响因素，以辛烷值的损失值为中心，采用最常用的高斯函数[15]计算点到中心的欧氏距离, 其表达式为

j=1,2,…,n

(6)

式(6)中：xn为主要影响因素，n=28；cj为第j个径向基神经元的中心；δ为高斯函数的方差，即光滑因子，再进入模式层进行加权求和。对于GRNN神经网络，确定其网络的结构和各神经元之间的连接权值，是以根据输入的样本为依据，故其需要确定的参数只有一个光滑因子，其一般取值范围[15]为[0,2]。本文以取值范围为基础，以输入的影响因素通过十折交叉验证的方法对δ进行一维寻优，以训练和实际的均方差为评价指标，将误差最小时的δ为最佳光滑因子进行构建网络。在实际辛烷值损失的计算中，当到第8次交叉验证时，得到最佳光滑因子为0.8，进而以它构建好预测辛烷值损失的GRNN网络模型。

3.3.4 随机森林模型

它是一种以决策树为基础的组合算法。针对本问题，采用多颗决策树分别独立计算辛烷值损失值，然后综合各个决策树的计算结果，以投票方式决定最终的结果，其过程如图5所示。具体计算步骤[16]如下。

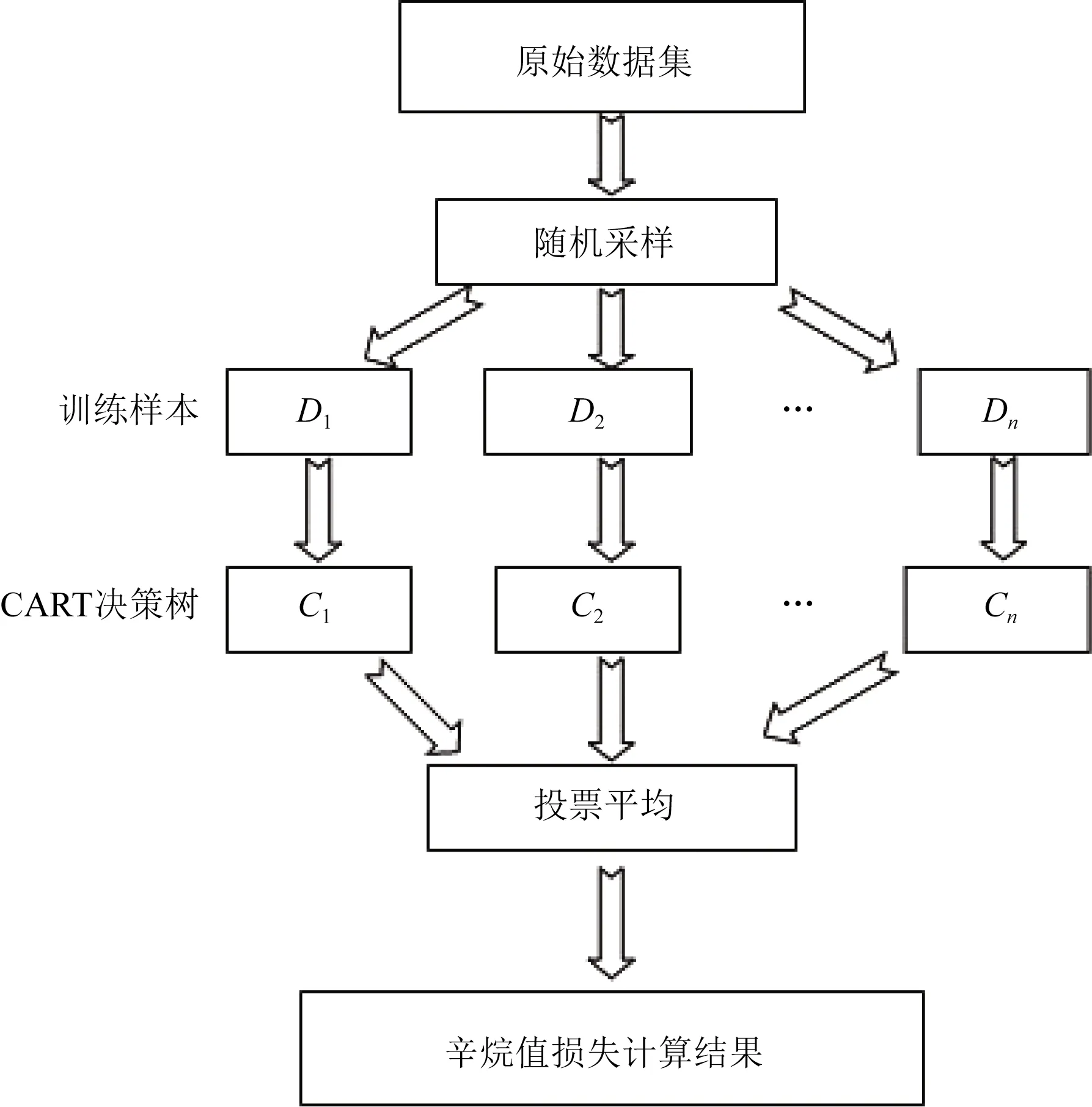
D1～Dn为随机采样后划分的训练样本；C1～Cn为对应匹配；D1～Dn所构建好的CART决策树

步骤1随机抽样。从训练的主要影响因素数据集中，通过有放回地 Boostrasp 抽样，生成若干组主要影响因素数据集，每组分为被抽中与未被抽中这两种，然后每组通过训练产生一颗决策树。

步骤2生长。训练每个决策树通过已有的主要影响因素数据进行。然后开始充分生长，具体表现为在每次分节点时，以若干影响因素为基础，然后以随机方式选取出特征，用Gini指标识别出最优特征来生长，持续到不能再生长为止。

步骤3校正。利用未被抽中的主要影响因素数据检验构建的随机森林模型精度，且模型的效果和泛化能力在一定程度上可以通过它进行检验。另外，还可以通过对未被选中的影响因素计算误差，确定计算辛烷值损失的最佳决策树的棵数且调整模型。如果效果不佳，甚至可重新构建模型。

步骤4将确定出的每棵决策树模型加权计算得到最终随机森林模型的预测结果。

此外，在构建随机森林过程中，有两个重要参数。一个为随机特征数，其值一般为自变量总数的1/3；另一个为决策树的棵数，它的确定一般是结合训练效果择优。根据资料[16]，基于以上思想和方法步骤，结合本问题特点以及训练模型的效果，设置随机特征数为9，决策树的棵数为800，进而构建好预测辛烷值损失的随机森林模型，简记为RF。

3.3.5K近邻回归模型

它是一种以实例为基础的方法。与前面几个方法不同，它是将模型的构建与未知属性特征的 定量计算同时进行，比较已知和未知的相似度，然后寻找最相似的K个样本用作未知的计算。根据刘长良等[17]的研究结果，提出计算辛烷值损失如下：以已有的影响因素数据集建立一个向量空间，再以某种距离度量为基础，本文选用欧氏距离，通过近邻样本的搜寻找到主要影响因素和所需计算辛烷值损失的点最接近的K个邻近点构成一个簇，对搜寻出的已知影响因素点进行投票，利用各簇中最多的类点对所求点进行平均计算，即K个邻近点输出的均值作为结果。

除此，搜寻近邻样本方法常用球树搜寻法和K-Dimension 搜寻法(即KD 树搜寻法)，本文在 Python 3.7环境下根据主要因素数据的特征自动选择最佳的搜寻方法。在K近邻回归建模中，只有一个需要确定的关键参数为K，如果K选取不当，则对构建的模型有较大的影响。对此，采用十折交叉验证，通过以训练和实际的均方差为评价指标，确定K值。可以由图 6得到，当K=15 时趋于平稳，故最佳K值为15，因此构建好预测辛烷值损失的K近邻回归模型，简记为KNN。

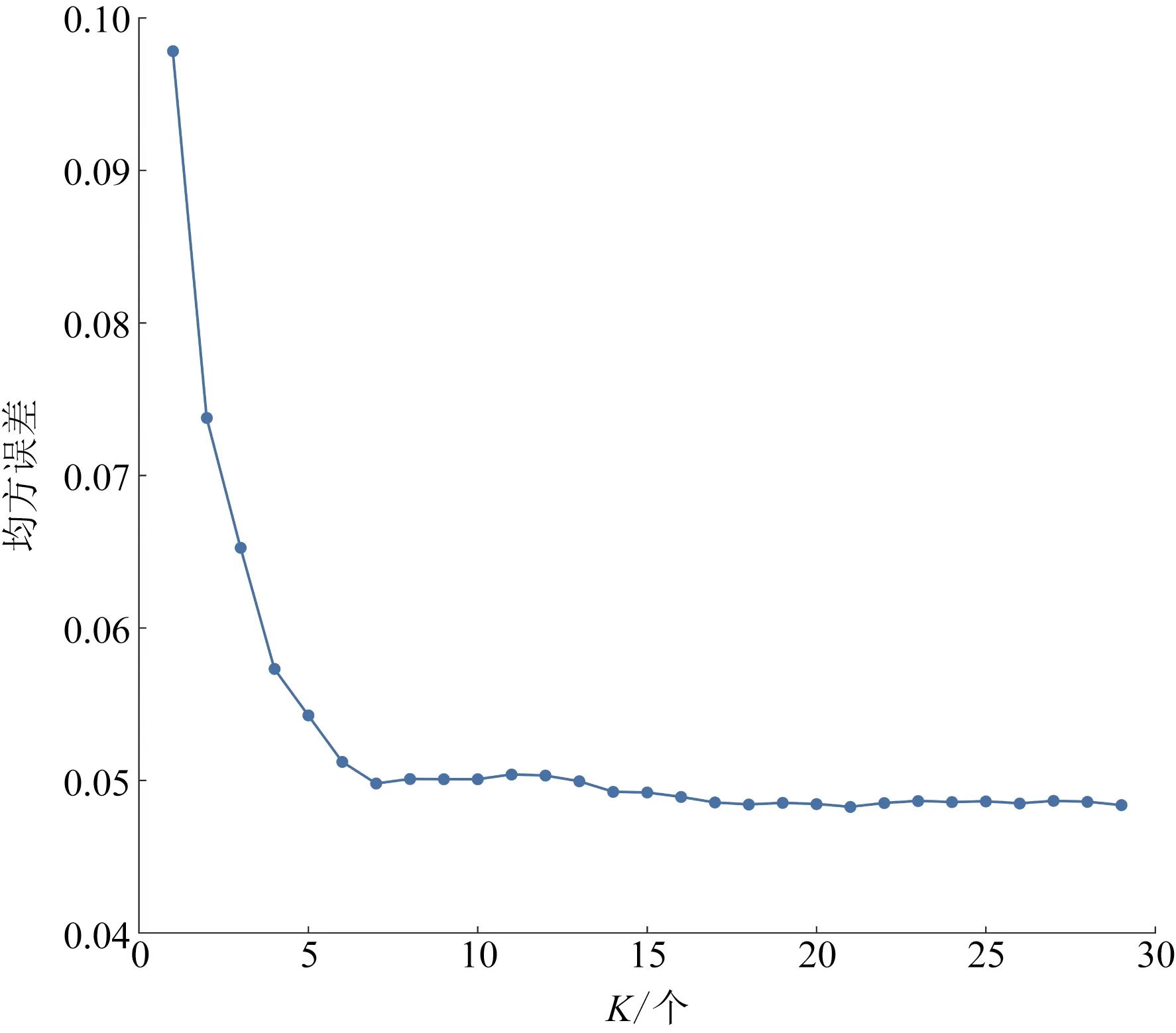
图6 K值变化图

4 实验过程及结果分析

基于前面的理论和方法，以某石化企业的积累数据为例，根据所提取的28个主要因素：烯烃、硫含量和氢油比等的操作变量，稳定塔顶压力和精制汽油出装置温度等计算辛烷值损失值。首先划分生成训练集D1和测试集D2；再采用随机打乱数据再进行划分，训练集D1为前面所构建模型所需的训练数据且占比为0.8，测试集D2为模型测试及评价的数据且占比为 0.2。为对模型有效训练和确定模型的关键参数，以前人的研究经验为基础，结合交叉验证的方法[12]，先将训练集D1划分为k个类似大小的互斥子集，即

D1=D11∪D12∪…∪D1k-1∪D1k

(7)

且不同子集间交为空集，每个子集Di都尽可能保持数据分布的一致性，从D1中通过分层采样而来。然后每次用k-1个子集的并集来训练，余下的用于测试，从而进行k次训练和测试。通过训练输出的值和实际值来计算均方差为评价指标确定模型的关键参数，模型经过以上训练达到最优拟合效果之后，再对测试集中辛烷值损失进行定量计算，最后通过对比检验模型的适用性和可靠性。

由于计算结果较多不便于直接展示，通过可视化图像将随机森林、支持向量机回归和K近邻回归的计算结果和如7(a)所示，K近邻回归作为中间枢纽比较，将其和两类神经网络预测结果如图7(b)所示。

图7(a)可以看出，预测辛烷值损失值最准确地为随机森林，支持向量机回归的计算偏差较大；而从图7(b)可以看出 GRNN 神经网络的预测结果最准确，单隐层BP神经网络偏差较大，K近邻回归和多隐层BP神经网络的计算结果比较接近。

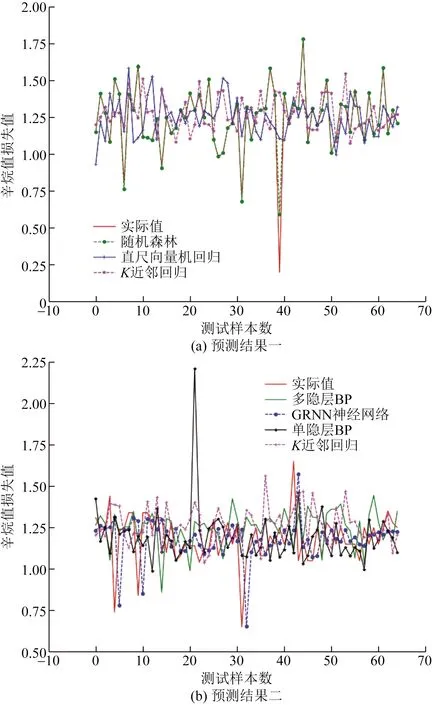
图7 辛烷值损失预测结果

由于只从结果图形直观可视化比较，存在一定主观性，为了更加客观进行分析比较，所以下面引入几个评价指标，分别为平均绝对误差(mean absolute error，MAE)、均方根误差(root mean square error，RMSE)、平均绝对百分比误差(mean absolute percentage error，MAPE)和拟合优度(goodness of fit，R2)。

(8)

(9)

(10)

(11)

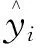
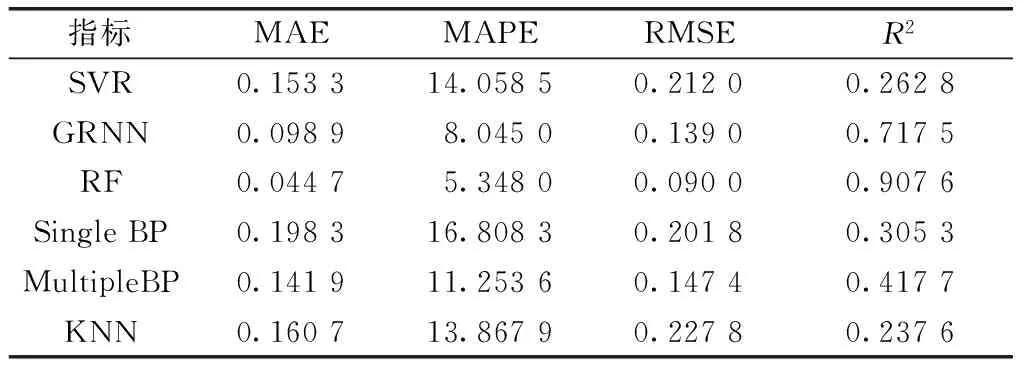
表3 各评价指标结果

除此，还对R2进行可视化分析，如图8所示。

由表3和图8可得，整体上随机森林的各项误差指标均与其他各方法相比最小，拟合效果最接近实际值，且实验过程中多次的随机交叉训练，对辛烷值损失的计算差异小，较为稳健。其次为GRNN神经网络，其各项误差指标也相对在较为合理的范围，且在收敛于优化回归面，表现为收敛于样本积聚最多的优化回归面。再其次为 BP 神经网络，虽然存在一些不足，但是通过合理增加其隐含层的层数可以对效果进行一定范围内的改善。最后，支持向量机回归和K近邻回归二者的计算效果比较接近，但精度存在的一定不足。

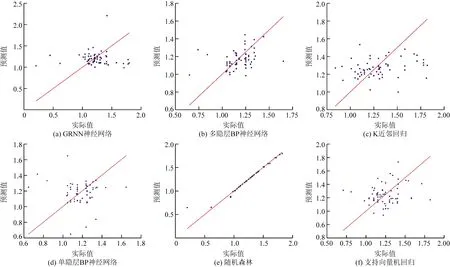
图8 各自的拟合优度图

此外为进一步结合实际应用，根据现行国家标准以及有关资料[18]，辛烷值为90～100的汽油差值|E|不大于0.2个单位则满足重复性要求，而再现性要求为差值|E|不大于 0.7个单位。随机森林计算辛烷值损失对应的终端辛烷值如表4所示。

由表4可得，RF计算结果有86.2%的在 0.7个单位以内，符合再现性要求，进一步说明构建的随机森林模型的合理性。综上所述，随机森林预测辛烷值损失的精度高且较为稳健，具有很大的实际应用意义。

表4 随机森林计算对应终端辛烷值

5 结论

(1)基于某石化企业所积累的数据，其存在影响辛烷值损失的众多因素，采用RFR-RFE算法提取主要影响因素。最终成功提取了28个辛烷值损失的主要影响因素，包含硫含量、烯烃、氢油比和稳定塔压力等，结合相关性分析和有关资料，得出所提取的因素为影响辛烷值损失特性的代表因素，进一步说明RFR-RFE算法在影响辛烷值损失特征提取上的合理性和有效性。

(2)针对汽油清洁化中辛烷值损失预测问题是多种复杂因素相互影响的辛烷值损失的定量计算问题，从数据驱动这一角度构建了可靠的高性能计算模型。以某石化企业为例，通过数据挖掘方法包括数据清洗、特征提取和挖掘建模进行分析计算。其实验结果表明：随机森林方法预测精度较高，是非常可靠的，能为在实际汽油清洁化中提前预测辛烷值的损失，进而提前做出合理的清洁化方案提供有力的技术支撑。