水下多电机协同推进及其动态面反步滑模控制

杨冠军，王伟然，闫景昊，朱志宇，曾庆军，戴晓强

(江苏科技大学电子信息学院，镇江 212100)

随着陆地资源有限与人类过度需求矛盾的日益突出，向海洋发展成为解决这一矛盾的必由之路。探索海洋、开发海洋离不开先进技术的支撑，水下机器人是水下探索的利器，是执行危险深海任务的重要载体。水下机器人工作在浅水区或狭窄复杂水域时会受到湍流的干扰，严重的紊流会使水下机器人产生偏航/侧翻等问题。高效、响应速度极快的水下机器人多推进电机协同控制可以有效抑制水下干扰，一定程度下消除湍流影响，稳定船体姿势，为惯性导航、路径跟踪、编队控制打下坚实基础。

现阶段多电机协同控制多用于轨道交通、电动汽车[1]与四旋翼飞行器。文献[2]将虚拟主轴同步控制(electronic virtual line-shafting，EVLS)与CRH02型高速列车牵引电机系统相结合，实验结果表明，该方法具有响应速度快、同步性好、适用范围广等优点。但是高速列车具有固定轨道，车辆同时受到外部与内在约束从而实现转向，但是水下机器人仅存在内在约束，远比轨道交通复杂[3]。文献[4]针对多电机协调控制同步性问题，提出了基于公铁两用车的多电机协同方案，并设计了超扭曲非奇异快速中断滑模函数，有效地推动了多电机控制方法的进步，但是公铁两用车控制聚焦于平面，水下驱动的自由度更高，需要对转矩分配作进一步的研究。文献[5]建立了一种双向电机驱动的四旋翼飞行器动力学模型，分析其双向推力作用下的运动过程并设计了相应的姿态位置控制器，水下工况的驱动方案与四旋翼极为相似，但是水流黏度远大于空气，该方案无法直接应用于水下机器人。

文献[6]利用改进型交叉耦合结构，设计多变量快速广义预测控制器，对网络化的多台电机完成了比例同步控制。文献[7]针对EVLS的从动轴电机采用滑模变结构技术(sliding mode control, SMC)设计了伺服单元的滑模速度控制器，结果表明，该方案能有效地降低滑模抖振，获得较高的同步精度。但在非线性干扰条件下该方案速度响应较慢，难以满足水下工况复杂下，对多推进电机系统控制的动态性能要求。文献[8]建立自抗扰模型并整定控制参数，来解决永磁同步电机(permanent magnetic synchronous machine，PMSM)跟踪精度问题，提升了PMSM在动力推进方面的响应速度等性能。目前，多电机协同的方案主要集中于同速同步控制，以上几种方法均没有考虑到多个从动轴给定不同参考速度的异速同步问题。缺少针对水下场景下多电机异速协同控制的研究。

针对以上主要问题，现提出一种应用于水下机器人的改进型EVLS，采用归一化比例同步系数分配方法来解决水下动力推进复杂非线性的工况问题与传统EVLS无法实现多电机异速协同的缺点。通过构造EVLS主轴与从动轴输入端，生成比例实时可调的参考速度以满足水下循迹时的要求，采用指数衰减转矩观测器代替计算转矩来反馈虚拟转矩；以反步控制为基础，引入有限时间滤波器[9]与准滑模tanh()函数设计PMSM推进电机的控制器[10-11]；以期这种改进型的EVLS多电机异速协同控制为提升水下机器人的动态响应速度、船体稳定性、推进效率提供理论基础。

1 多电机协同控制策略

1.1 EVLS多电机协同控制

水下机器人在大幅度路径改变时对多电机的异速协同有较高要求。EVLS控制通过建立传动特性与实际机械轴相同的虚拟主轴来模拟实际机械轴[12]，将实际从动轴上的负载力反馈给虚拟主轴，通过主轴控制器的计算，使得虚拟主轴与实际从动轴之间实现扭矩平衡。虚拟主轴驱动力矩为

(1)

式(1)中：Tref为虚拟主轴驱动力矩；b为主轴阻尼系数；Km为虚拟主轴的输入端的弹性参数；ωref为理论设定角速度；ω*为虚拟主轴输出角速度；t为系统运行时间。其动力学方程为

(2)

式(2)中：Trefi为各实际从动轴电机反馈力矩；以3台电机为研究对象，则有i=1,2,3；θ*对应主轴的角位移；J为主轴的转动惯量。

主轴控制器通过反馈调节和速度分配来控制多电机驱动系统的同步运动。传统EVLS技术只能协同相同转速的多个电机，因此这里设计一种归一化的系数分配方法，建立动态异速的多电机EVLS控制方法。同时，水下机器人由于轨迹跟踪与外部湍流干扰，每个实际从动轴电机需要动态调整，因此其负载转矩具有时变性和不可测性，使用观测器替代转矩计算输出虚拟转矩。

改进型EVLS多电机协同控制方案，如图1所示，该方案由主轴控制、基于归一化的同步比例系数分配方法、从动轴控制器、电机矢量控制系统4部分组成。

ωd1,d2,d3为各推进电机分解参考转速；为各观测器输出转矩，代替Trefi；udi、uqi为各电机d、q轴的电压；idi、iqi为各电机d、q轴的电流；为各从动轴的参考旋转角速度；ωi为电机实际旋转角速度

1.2 基于归一化系数分配的改进型EVLS

为保持船体姿势，水下机器人需要根据工况实时改变推进电机的速度与推力，从而实现六自由度运动。此时水下机器人各个推进器产生的合推力矢量为

τ=B(β)u

(3)

为推进器输出的推力矢量；B(β)为推进器的矢量布置矩阵。

将水下机器人各个推进器所产生的单力矢量在体坐标系下进行等效分解，得到单个推进器可以提供的最大纵向、横向、垂向推力，横倾、纵倾和偏航力矩。根据螺旋桨转速与推力的关系建立期望推力分配公式为

τd=Λωd

(4)

式(4)中：τd为六自由度期望分配推力矢量；Λ=diag(k1,k2,k3,k4,k5,k6)为权重对角阵[13]；k为各方向的权重系数与放大倍数乘积，根据水下机器人直行、转向、俯仰的状态实时改变；ωd为各台推进电机分解参考转速。

(5)

经过推力分配的推进器输出矢量u，归一化控制的结构如图2所示。

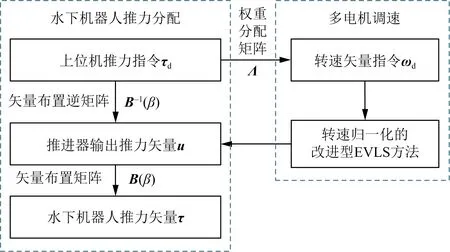
图2 归一化控制结构框图

将水下机器人所有的推进器在体坐标下等效为x、y、z轴水平安装的3台推进电机，轨迹跟踪与抵御外部湍流干扰即可简化为3台电机实时转速控制。根据比例同步要求，定义初始比例系数[14-15]：比较3台电机的输入速度，将最高转速轴定义为ωref，将比例系数最大的电机定义为虚拟主轴转速参考值。

ωref=max(ωd1,ωd2,ωd3)

(6)

式(6)中：ωd1、ωd2和ωd3为所设3台电机的分解参考速度。计算3台电机的比例系数μ1、μ2、μ3，即

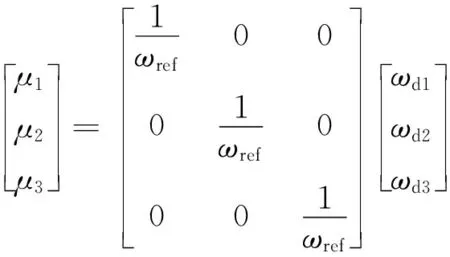
(7)

将传动比系数与主轴动力学方程[式(2)]结合，得到各从动轴的输入转速。经过归一化计算后各从动轴的参考转速为

(8)

式(8)中：s为拉普拉斯积分。从动轴的反馈转矩为

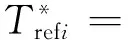
(9)

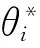
归一化的速度控制同时考虑水下动力分配与电机参考转速给定，实现比例实时可调的异速协同控制。如此，每个从动轴推进电机均能根据水下大幅度转向动作等实际工况进行异速协同，保证水下机器人在路径跟踪与转向过程中的平滑过渡，实现更快更高效的动作。水文环境复杂时，推进电机会受到强烈的外界随机非线性的水流干扰，影响电机的同步性与跟踪能力，因此需要设计抗扰性能较强的单电机控制器。

2 推进电机有限时间动态面反步滑模控制

为提高改进型EVLS的抗干扰性能，基于反步控制设计从动轴推进电机的非线性控制器，以推进电机的数学建模为基础，将有限时间滤波器于tanh()滑模函数结合来增强系统鲁棒性能与收敛速度，结合指数衰减观测器获取高精度的实时转矩数值。

2.1 推进电机数学模型

将改进型EVLS系统中的电机数设定为3，建立永磁同步电机转子磁场定向控制的数学模型[16]，其中任意的第i台推进电机的电压方程为

(10)

采用idi=0的控制策略时，电磁转矩方程为

(11)

第i个PMSM的动力学方程为

(12)

式中：Ldi、Lqi为d、q轴的电感；Ri为定子电阻；pi为极对数；Ji为转动惯量；Tei为电磁转矩；TLi为负载转矩；ψai为交链磁链。

在使用idi= 0控制的情况下[17]，推进电机基于同步旋转坐标系的运动方程和电压方程分别为

(13)

2.2 有限时间动态面反步滑模控制器

为提高单电机控制的稳定性，从PMSM系统方程选取状态变量分解为子系统。随后给每一个子系统设计虚拟控制律，逐步设计最终得到系统的实际控制律uqi、udi，使整个系统达到期望的性能。

第1步定义第1个误差变量为

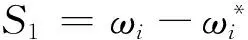
(14)

根据PMSM运动和电压方程[式(13)]，S1的时间导数为

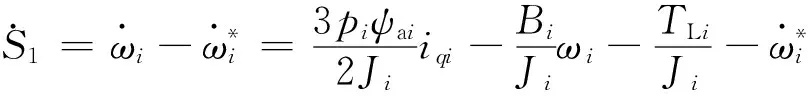
(15)

(16)

式(16)中：l1>0和ε>0为设计参数。

引入快速有限时间收敛的非线性滤波器对虚拟控制信号进行滤波，消除由于对虚拟信号求导而产生的微分膨胀问题。滤波器方程为

(17)

(18)

(19)

第2步定义第2个、第3个误差变量为

S2=iqi-zf

(20)

(21)

从式(18)、式(20)可以得出：

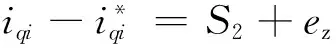
(22)

根据式(13)，S2、S3的导数为

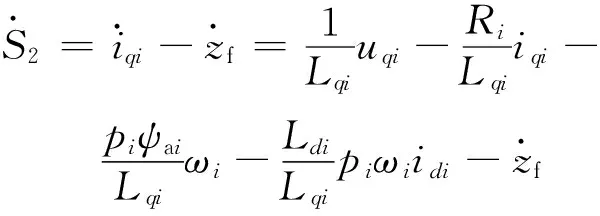
(23)

(24)

定义滑模控制的切换函数为

σ=k1S1+S2

(25)

式(25)中：k1> 0为设计参数。

对σ求导可得

(26)

对于实际从动轴电机[式(13)]，构建闭环控制系统，选取Lyapunov函数为

(27)

(28)

则可以后续调节计算参数l2、l3、α、β、k1，使实际从动轴电机系统半全局一致最终有界。引入连续可导的tanh()函数，设计最终实际控制信号为

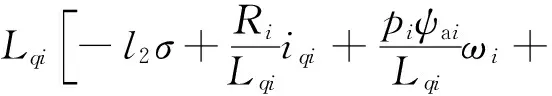
(29)

(30)

由不等式[11]：

(31)

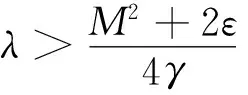
对于式(31)两边在[0,t]内积分，可得

(32)

式(32)中：闭环系统所有信号S1、ez、σ半全局一致最终有界。代入式(29)、式(30)，得到为保证推进电机控制系统优异的启动性能与抗干扰性能所设计的输出控制量uqi和udi。有限时间动态面反步滑模控制器(dynamic surface backstepping sliding mode controller，DBSMC)关注推进电机的抗干扰性能与系统收敛速度，在保证水下动态响应速度的同时，增强改进型EVLS控制系统的抗干扰性能。

2.3 指数衰减观测器

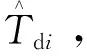
考虑到外部水流干扰与动态响应延时所造成的测量误差，由式(11)和式(12)建立转矩扩展状态方程为

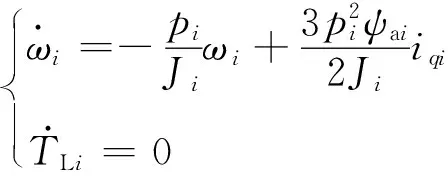
(33)

(34)

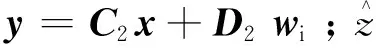
(35)

在零初始状态下，选择性能函数为

(36)

式(36)中：

(37)

当Q<0，有F< 0，‖Δz‖2<γ‖wi‖2适用于任何wi≠0，相当于‖GΔzw‖<γ。求解Q<0，可得到观测器的干扰抑制增益K。

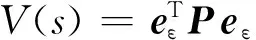
(38)

如果存在标量α>0令

(39)

假设观测误差eε(t0)在t0时刻，可以得

(40)

式(39)中：λ为P矩阵的特征值。当式(38)成立时，标量α表示观测误差的指数衰减率。

为进一步提高系统的抗扰动性能，将观测器的输出作为估计的集总扰动被馈送到控制器作为补偿部分，以增强鲁棒性能，式(29)更新为

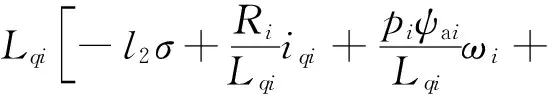
(41)

由状态观测器式(34)可知，结合扰动抑制率K和观测误差的指数衰减率α，将其应用于改进型EVLS，直接反馈观测转矩，主轴将快速响应较大的负载变化，能更准确地反映从动轴动态关系[18]。

3 仿真实验

根据PMSM的动力学模型方程，对改进型EVLS控制的多电机系统进行仿真实验。将水下机器人所有的推进电机分类为主推电机1，功率2.2 kW；侧推电机2，功率1.8 kW和升降推进电机3，功率1.5 kW。主轴的转动惯量J= 0.003 kg·m2。电机采用矢量控制方案，电机具体参数如表1所示。

表1 推进电机的参数

根据波浪力与海流干扰公式[19]，加入随机波浪扰动负载来验证对系统鲁棒性的影响，此外电机1、电机3的负载在0.375、0.455、0.85、1.125 s时产生幅度为50%负载变化，模拟较大的瞬时海流干扰，电机2仅设置随机波浪扰动，如图3所示。

图3 工况1考虑随机持续干扰的负载转矩

将水下机器人设置为直航工况1，电机1的参考转速设置为1 200 r/min，电机3的参考转速为800 r/min辅助下潜，此时μ1∶μ2∶μ3=3∶0∶2。多电机比例同步控制系统的速度响应如图4所示。

图4 工况1下DBSMC控制的多电机比例同步转速响应

仿真结果表明，在归一化算法的分配原则下，电机1的参考速度计算为1 200 r/min，其他电机与其呈比例关系输出。改进型EVLS控制下的推进电机的受干扰影响小，启动时系统稳定时间为0.013 s，负载变化时产生0.29%的超调量。直航时受到水流干扰恢复速度为0.004 s，超调量为0.27%。电机在启动，直航，停止等工况下运行响应速度快，系统具有较强的鲁棒性与稳定性。

验证比例同步控制的速度切换性能，将3台电机的参考转速设置为800～1 200 r/min变化的工况2。循环输入3台电机的参考转速，模拟航向调整时的转速变化，电机1、电机2和电机3的转速输出将显示比例同步的效果。系统负载加入随机波浪扰动与海流干扰，如图5所示。多电机比例同步控制系统的速度响应如图6所示。

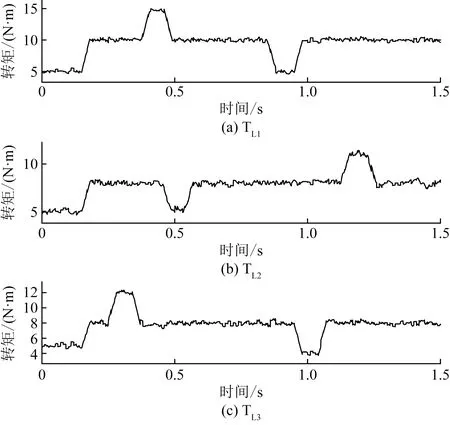
图5 工况2考虑随机持续干扰的负载转矩

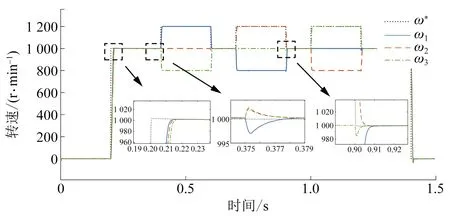
图6 工况2下DBSMC控制的多电机比例同步转速响应

结果表明，DBSMC控制的推进电机的稳定时间为0.014 s，负载变化时产生0.3%的超调量，恢复时间0.003 s。DBSMC控制系统在抑制超调和系统稳定速度快，抗干扰性能较强。图7为各电机之间的同步转速误差。DBSMC控制下的3台电机，误差消除时间小于0.01 s。结果表明，归一化方法控制能保证多电机的异速同步过程，DBSMC控制的从动轴电机的同步性能较强。

e21为电机1、电机2的转速误差；e31为电机1、电机3的转速误差；e32为电机2、电机3的转速误差

对比文献[10]中的SMC方法与本文提出的DBSMC方法，验证控制方法的有效性，给出步进从800 r/min到1 000 r/min再到1 200 r/min时的电机参考转速跟踪，如图8所示，添加的随机干扰与图4电机1相同。

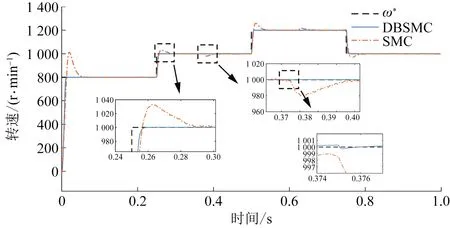
图8 PMSM速度响应曲线

当参考转速发生变化时，SMC控制下的推进电机的超调量达到4.9%，稳定时间为0.055 s；在连续波浪扰动下，电机转速波动较大，负载变化时产生1.5%的超调量。DBSMC控制系统的稳定时间为0.012 s，无超调量。DBSMC控制系统对持续扰动有很好抑制效果，负载转矩较大变化时转速0.01 s内恢复。

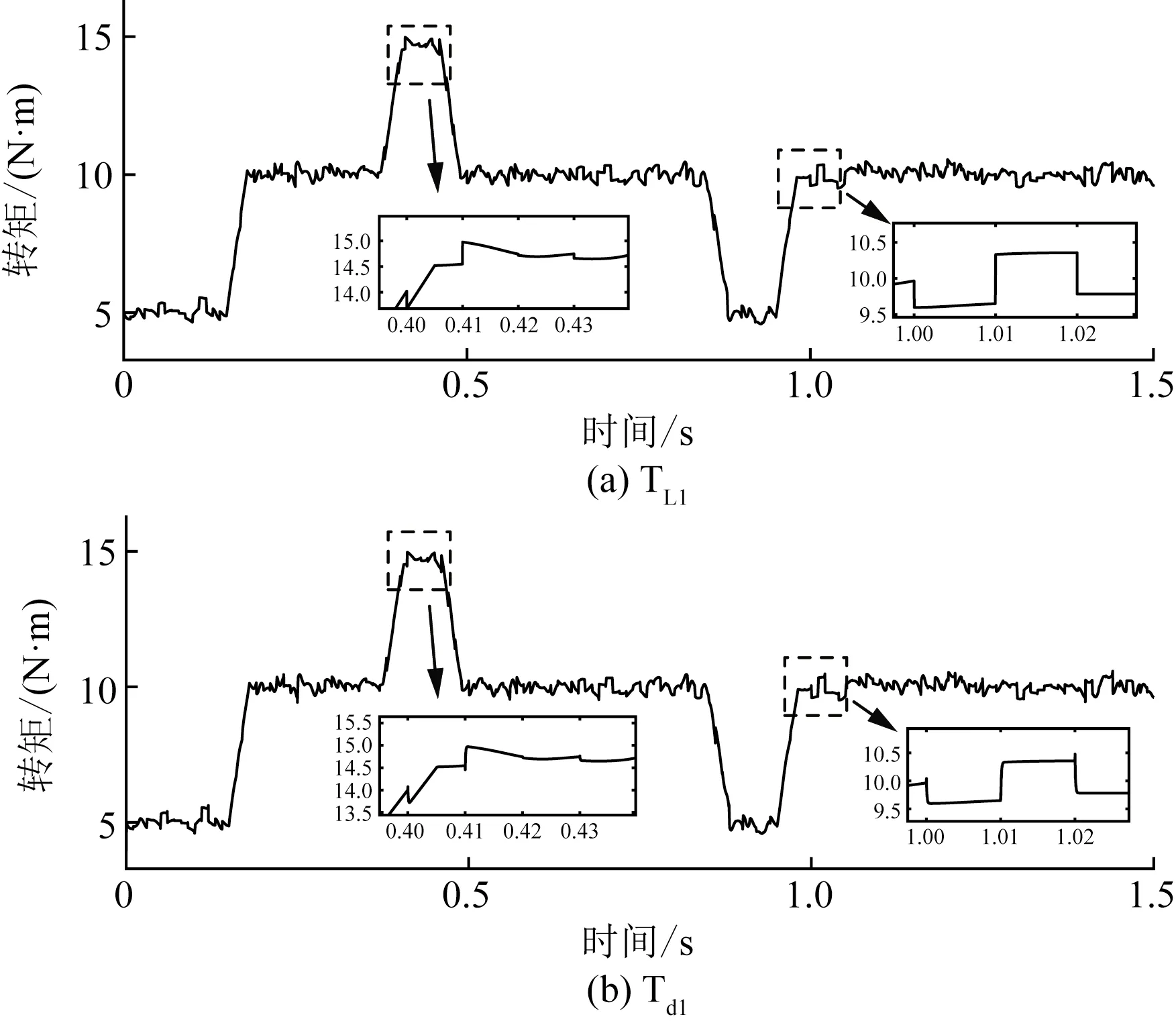
图9 指数衰减观测器的转矩观测波形

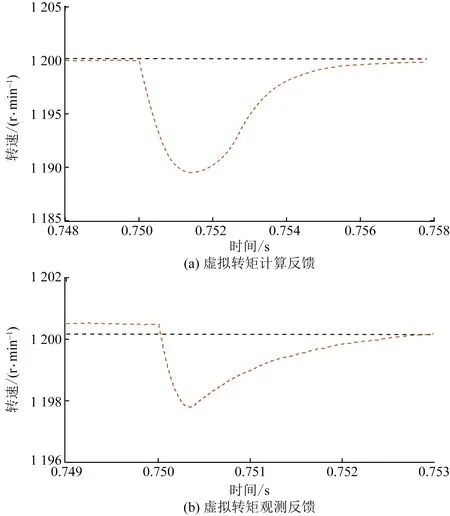
图10 主轴反馈控制下的推进电机转速

图10(a)是从动轴计算转矩反馈下的电机的转速，当0.75 s负载转矩发生较大变化时，转速下降0.8%。图10(b)是有观测器反馈转矩的电机转速，转速下降0.16%。转矩前馈补偿也进一步增强电机转速的控制性能和抗干扰性能。

4 结论

将多电机比例同步控制技术应用于水下机器人动力推进领域，以多电机推进模型为对象，对其建模与控制进行了研究。

(1)分析了基于EVLS的多电机模型，设计了归一化比例同步分配方法改进EVLS结构，使其更适用于水下动力推进控制。

(2)为消除复杂水域波浪对推进电机的影响，设计了DBSMC，有效提升了推进电机的转速跟踪性能与抗干扰性能。

(3)引入了指数衰减转矩观测器，保证数据实时更新的同时兼顾估算精度，从而提高主轴响应速度，增强系统的抗干扰性。

(4)与传统的EVLS方法相比，基于改进型EVLS的DBSMC使控制系统摆脱了单一同步控制的局限性。仿真结果表明，该方法在连续不确定扰动条件下具有较强的鲁棒性，为多电机水下推进的进一步发展提供了新的思路。