含缺陷石墨烯弹性性能的分子动力学模拟

邓雅丹，周昆，黄君，黄立新,2*

(1.广西大学土木建筑工程学院，南宁 530004; 2.广西大学工程防灾与结构安全教育部重点实验室，南宁 530004)

石墨烯是由碳原子组成的蜂窝形纳米材料，它的比表面积大、稳定、柔韧并且具有良好的导电性、导热性、光学特性和机械性能，在电子[1-3]、航空航天[1]、新能源电池[2, 4]、生物医学[5-6]等领域都具有良好的应用前景，石墨烯性能的研究具有十分重要的意义。为了更好地研究石墨烯的性能，石墨烯的制备方法也在不断发展，范金辰[7]采用超声剥离法得到功能化的石墨烯片层；Kumar等[8]采用原位微波法制备三维(3D)还原氧化石墨烯纳米片；陈吉[9]采用化学气相沉积法制备石墨烯。以上研究为高性能石墨烯的制备提供了简便、有效的方法。石墨烯在各个领域的研究，都是基于理想即无缺陷的石墨烯，然而在石墨烯的制备过程中，或多或少都会产生一定的缺陷，这些缺陷会对石墨烯的性能产生一定的影响，因此研究含缺陷石墨烯的性能是一项十分重要的工作。

石墨烯的缺陷主要有3种：空位缺陷、表面吸附杂质缺陷和拓扑缺陷[10]。空位缺陷包括单空位缺陷、双空位缺陷和多空位缺陷。所谓的空位缺陷，就是因结构缺失原子，所造成原有位置的空缺，因缺失原子数目的不同，其名称也不同，缺失一个原子即单空位缺陷，缺失两个相邻原子即双空位缺陷，缺失3个及3个以上相邻原子即多空位缺陷。表面吸附杂质缺陷即当石墨烯的原子离开晶格，与其相邻的3个C原子各多出一个悬空键，以此来吸引外来原子。拓扑缺陷常见的是Stone-Wales缺陷(以下简称SW缺陷)，SW缺陷不含原子的缺失，它只是其中一个C-C键通过键角旋转90°，缺陷部分的形状由4个六边形变成2个五边形和2个七边形。

He等[11]基于分子动力学模拟研究了Stone-Thrower-Wales(STW)缺陷的取向和倾斜角对石墨烯力学性能的影响，可知STW-1缺陷和STW-2缺陷的石墨烯，其扶手型方向的强度与锯齿型方向的强度具有差异，且机械性能取决于缺陷的倾斜角。Mortazavi等[12]采用分子动力学模拟，研究了点空位、双空位和Stone-Wales缺陷对单层石墨烯片热导率和拉伸响应的影响，可以得到石墨烯的弹性模量、拉伸强度和断裂应变随着缺陷浓度的增加而降低，且热传导更容易受到缺陷影响的结论。Lei等[13]通过分子动力学模拟，研究了各种点缺陷和裂纹对4种石墨烯同素异形体力学性能的影响，研究发现它们的杨氏模量相较于拉伸强度而言，对各种类型的点缺陷更不敏感，而对裂纹而言，其杨氏模量和拉伸强度都显著下降。Ajori等[14]利用分子动力学模拟，研究了映射缺陷和随机缺陷对石墨烯同素异形体γ-graphyne的杨氏模量、极限应力和应变以及泊松比的影响，结果表明，γ-graphyne的强度和刚度低于石墨烯，此外，随机缺陷的力学性质变化比映射空位缺陷大。

由于石墨烯的缺陷是不可避免的，缺陷对石墨烯弹性性能的影响比较复杂，缺陷的位置、形状以及原子缺失率如何影响石墨烯的弹性性能，仍然存在需要解决的问题，有必要开展进一步的研究工作。因此，现采用分子动力学模拟的方法，研究空位缺陷的位置、形状以及原子缺失率对石墨烯弹性性能的影响，探究空位缺陷的位置、映射横向长条状缺陷、映射纵向长条状缺陷、映射圆孔状缺陷和随机缺陷等因素导致石墨烯杨氏模量减少的规律。

1 分子动力学方法和理论

基于分子动力学理论，采用软件Materials Studio(MS)进行力学性能计算。MS是一款用于创建分子结构模型，并对模型进行计算分析以研究其性质的模拟软件[15]。采用脚本进行模拟计算，MS的脚本采用一种功能强大、应用广泛且灵活性强的计算机程序Perl语言进行计算。

在模拟的过程中，由于物体的宏观性质需要足够多的微粒，而计算机无法满足其庞大的计算，就要考虑边界部分所带来的影响，因此，为了消除边界效应，该模型采用周期性边界条件。COMPASS(condensed-phase optimized molecular potentials for atomistic simulation studies)力场[16]用于原子模拟，COMPASS的能量表达式[17]为

Utotal=Ubonded+Unonbonded

(1)

Ubonded=Udiagonal+Ucross-coupling

(2)

Unonbonded=Uij+Uelec

(3)

式中：Utotal为总能量；Ubonded为键合项能量；Unonbonded为非键合项能量；Udiagonal为对角的交叉偶合项；Ucross-coupling为非对角的交叉偶合项，非键合项能量为范德华能Uij与库伦能Uelec之和。

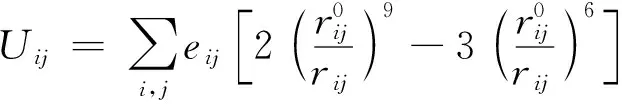
(4)

(5)

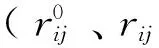
(6)

(7)

本模型是在NPT系综[19]即恒定的粒子数、恒定的体积及温度下进行的，同时采用可控制各向异性加压的Souza-Martins恒压器进行调节，时间常数为10 ps。为了使温度保持稳定，采用Nose-Hoover-Langevin(NHL)恒温器，在恒温器变量中引入摩擦项和噪音项，使其收敛速度更快。并且在所有情况下都使用1 fs的固定时间步长。

2 石墨烯分子动力学建模及杨氏模量计算方法

2.1 建模步骤

(1)在MS 8.0软件中导入石墨烯的单晶胞模型，创建含有25×15×1个正六边形(碳原子数为1 500)的石墨烯超晶胞模型，Lx=6.047 nm，Ly= 6.434 nm，如图1所示。

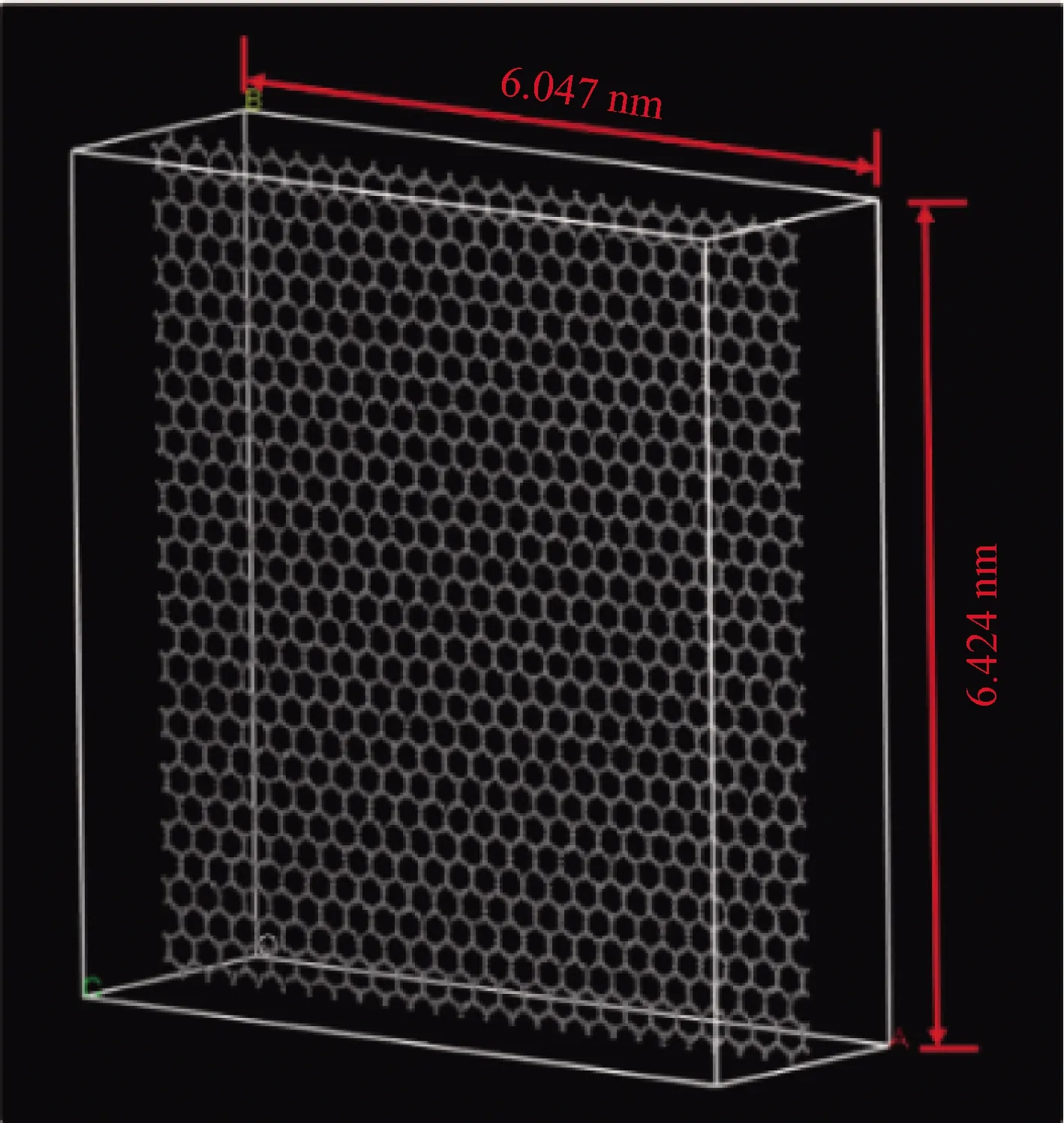
图1 石墨烯分子动力学模型

(2)对模型进行几何优化，细化结构的几何形状，直到结构的总能量被最小化，优化后的结构对应于势能面中的最小值。

(3)采用脚本对优化后的模型分别沿y方向和x方向施加应力，如图2(a)所示。设置初始应力值为20 GPa，然后依次递增，每次增加20 GPa，每个应力值的平衡步数设置为500，每500 步生成一帧，每一帧统计一次应力应变数值。

(4)当应力大小增大至500 GPa时，可得出对石墨烯模型施加y方向的应力-应变数值。

(5)重复同样的步骤，对模型施加x方向的应力，如图2(b)所示，即可得出石墨烯模型对应的应力-应变数值。

图2 石墨烯模型施加应力

2.2 杨氏模量的计算方法

按照2.1节的建模步骤，分别沿y方向和x方向施加应力，即可得出石墨烯模型对应的应力-应变数值，如表1所示。根据表1绘制应力-应变关系图，如图3所示。从图3中可以发现，当应变达到0.3时，应力-应变曲线出现明显的拐点，因此采取应变为0～0.25的曲线段进行最小二乘法拟合，计算杨氏模量[20-22]。

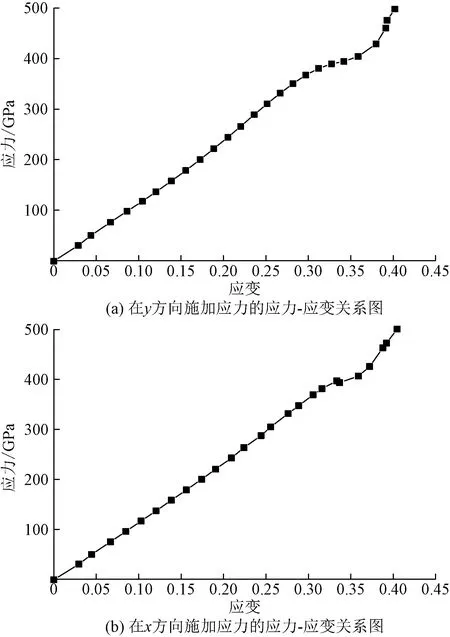
图3 石墨烯模型施加应力后的应力-应变关系图

设应变为ε，应力为σ，E为杨氏模量，则方程为

σ=Eε

(8)

采用最小二乘法进行直线拟合[23]，得到杨氏模量计算公式为

(9)

将表1中应变为0～0.25区间内的应力-应变数值组代入式(9)，即可求出杨氏模量E的值，即Ey=1.179 TPa，Ex=1.161 TPa。

3 结果与分析

3.1 无缺陷石墨烯的杨氏模量

通过MS软件计算，对表1应力-应变数值组进行最小二乘法的直线拟合，所得石墨烯杨氏模量与文献结果进行对比，如表2所示。从表2可以看出，石墨烯杨氏模量的文献值在1.00～1.24 TPa，本文模型的杨氏模量值在合理范围之内，说明本文方法适用于研究石墨烯的力学性能。

表1 模型施加应力后的应力-应变数值

表2 石墨烯的杨氏模量与文献结果对比

3.2 空位缺陷位置对石墨烯力学性能的影响

由于缺陷是不可避免的，缺陷会对石墨烯的力学性能产生一定的影响，为了研究缺陷产生的位置是否也会对石墨烯的性能产生影响，设计了两组单空位缺陷，第一组为纵向方位缺陷，包括上边缘缺陷、偏上方位缺陷、中间部位缺陷、偏下方缺陷、下边缘缺陷，模型示意图如图4所示，分子动力学模拟结果如图5所示；第二组为横向方位缺陷，包括左边缘缺陷、偏左方位缺陷、中间部位缺陷、偏右方位缺陷、右边缘缺陷，模型示意图如图6所示，分子动力学模拟结果如图7所示。

图4 y方向空位缺陷模型

图5 y方向空位缺陷分子动力学模拟结果

图6 x方向空位缺陷模型

图7 x方向空位缺陷分子动力学模拟结果

分别对这两组不同位置的含缺陷模型施加y方向和x方向的应力，对所得应力-应变进行最小二乘法的直线拟合，求出石墨烯的杨氏模量。纵向方位缺陷和横向方位缺陷的石墨烯杨氏模量计算结果分别如表3所示。

表3 含缺陷石墨烯杨氏模量的结果

由表3可知，纵向方位含缺陷石墨烯的杨氏模量均小于无缺陷石墨烯杨氏模量。施加y方向应力时，中间位置缺陷石墨烯的杨氏模量值为1 175.42 GPa，小于上下两边位置缺陷石墨烯的杨氏模量，这是因为施加应力和缺陷的方向都是纵向的，当施加应力与缺陷的方向相同时，不易造成模型的破坏。此时，缺陷对模型的稳定性影响较小，而中间位置的缺陷对模型稳定性影响相对于上下两边位置的缺陷更大；施加x方向应力时，中间位置缺陷石墨烯的杨氏模量值为1 156.20 GPa，大于上下两边位置缺陷石墨烯的杨氏模量，这是因为施加应力的方向是横向的，而缺陷的方向是纵向的，当施加应力方向与缺陷方向垂直时，较易造成模型的破坏。此时，缺陷对模型的稳定性影响较大，而上下两边位置的缺陷对模型稳定性影响相对于中间位置的缺陷更大，即上下两边缘更容易使得模型破坏。

当所施加的应力方向与缺陷方向相同，缺陷对模型的稳定性影响较小；当所施加的应力方向与缺陷方向垂直，缺陷对模型的稳定性影响则较大。

可见，单空位缺陷的位置对石墨烯杨氏模量有一定的影响，当缺陷对模型稳定性影响较大时，边缘位置缺陷对于模型稳定性的影响相对于中间位置缺陷更大，即边缘位置缺陷更容易使模型破坏；当缺陷对模型稳定性影响较小时，边缘位置缺陷对于模型稳定性的影响相对于中间位置缺陷更小。

3.3 空位缺陷的缺失率对石墨烯力学性能的影响

由于缺陷会对石墨烯的力学性能产生一定的影响，为研究缺失原子的数目和形式对石墨烯性能的影响，设计了两种类型的空位缺陷，即映射缺陷和随机缺陷。这里的映射缺陷为多空位缺陷，指的是缺失的位置聚集在一个固定的位置，设计了映射横向长条状缺陷、映射纵向长条状缺陷、映射圆孔状缺陷。随机缺陷属于单空位缺陷，指的是缺失的原子随机分布在各个位置，所谓的随机，也就是随着实验次数的不同，缺失位置以及实验结果都不一样，但由于是随机的，其结果也会在一定的范围内波动。

为了更好地说明空位缺陷对石墨烯力学性能的影响，设计并研究了映射缺陷和随机缺陷的缺失率对其杨氏模量的影响。缺失率Q为

(10)

式(10)中：n为缺失原子的个数；N为完美石墨烯总原子个数。

除了缺陷之外，还考虑石墨烯手性对杨氏模量的影响。如图8(a)所示，石墨烯的手性由手性矢量[22]C定义，即

C=n1a1+n2a2

(11)

式(11)中：a1、a2为晶胞矢量；n1、n2为整数(n1≤n2)。

根据矢量C或手性角度α，可将石墨烯分为锯齿型和扶手型。当荷载方向为y方向，手性矢量C与x轴的夹角α=0°，即锯齿型(Zigzag)，如图8(b)所示；手性矢量C与x轴的夹角α=30°，即扶手型(Amchair)，如图8(c)所示。

图8 石墨烯手性示意图

对各种类型缺陷缺失不同数目原子的模型均进行计算，计算时分别在y和x方向施加应力，并对其应力-应变曲线在应变为0～0.25区间内进行最小二乘法拟合，结果即为石墨烯锯齿形方向和扶手型方向的杨氏模量。

3.3.1 映射横向长条状缺陷

映射横向长条状缺陷是由无缺陷石墨烯片的中间位置原子开始，往横向两边方向依次缺失原子，模型示意图如图9所示，分子动力学模拟结果如图10所示。石墨烯片的原子缺失率与杨氏模量的关系如图11所示。从图11中可以看出，随着缺失率的增加，石墨烯的杨氏模量不断减小，而锯齿型石墨烯的杨氏模量减小得更明显，扶手型石墨烯的杨氏模量只是在小范围内减小。原因是原子是横向缺失的，当缺失原子数越多，缺陷的形状就越接近横向长条状，此时，施加y方向应力(锯齿型)，模型就越不稳定，易造成模型的破坏；而施加x方向的应力(扶手型)，对模型的稳定性造成的影响不大。由此可见，对于映射横向长条状缺陷，随着缺失率的增大，石墨烯的杨氏模量不断减小，并且锯齿型石墨烯的杨氏模量减小得更快。

图9 映射横向长条状缺陷模型

图10 映射横向长条状缺陷分子动力学模拟结果(扶手型)

图11 映射横向长条状缺陷石墨烯的缺失率与杨氏模量的关系

3.3.2 映射纵向长条状缺陷

映射纵向长条状缺陷是由无缺陷石墨烯片的中间位置原子开始，往纵向两边方向依次缺失原子，模型示意图如图12所示，分子动力学模拟结果如图13所示。石墨烯片的原子缺失率与杨氏模量的关系如图14所示。随着缺失率的增加，石墨烯的杨氏模量不断减小，而扶手型石墨烯的杨氏模量减小得更明显，锯齿型石墨烯的杨氏模量只是在小范围内减小。原因是原子是纵向缺失的，当缺失原子数越多，缺陷的形状就越接近纵向长条状，此时，施加x方向应力(扶手型)，模型就越不稳定，易造成模型的破坏；而施加y方向的应力(锯齿型)，对模型的稳定性造成的影响不大。由此可见，对于映射纵向长条状缺陷，随着缺失率的增大，其杨氏模量不断减小，并且扶手型石墨烯的杨氏模量减小得更快。

图12 映射纵向长条状缺陷模型

图13 映射纵向长条状缺陷分子动力学模拟结果(扶手型)

图14 映射纵向长条状缺陷石墨烯的缺失率与杨氏模量的关系

3.3.3 映射圆孔状缺陷

映射圆孔状缺陷是由无缺陷石墨烯片的中间位置原子开始，往四周依次缺失原子，缺失原子的部位为圆孔状，模型示意图如图15所示，分子动力学模型如图16所示。由于缺失原子后的形状接近圆孔状，因此缺失的数目并不是固定的。石墨烯片的原子缺失率与杨氏模量的关系如图17所示。由图17可知，随着缺失率的增大，锯齿型和扶手型石墨烯的杨氏模量均减小，并且锯齿型的杨氏模量比扶手型的大。

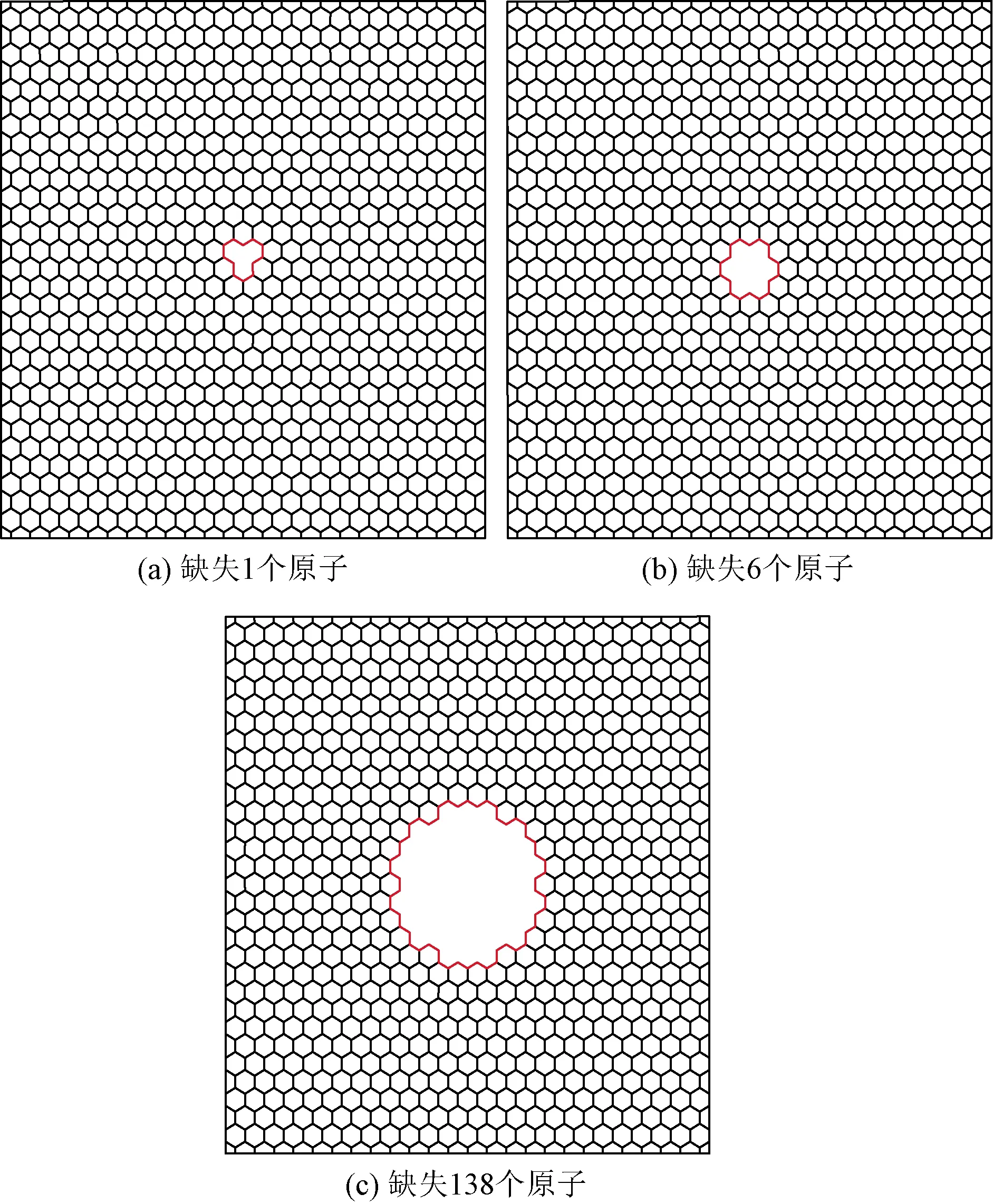
图15 映射圆孔状缺陷模型

图16 映射圆孔状缺陷分子动力学模拟结果

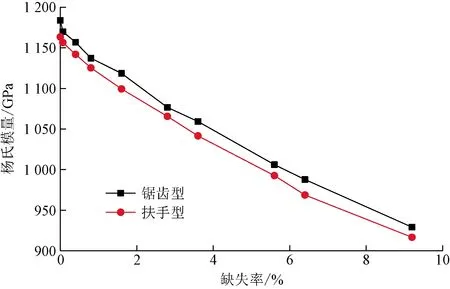
图17 映射圆孔状缺陷石墨烯的缺失率与杨氏模量的关系

3.4 随机缺陷

对于随机缺陷石墨烯的分子动力学模拟，采用如下步骤进行。

(1)采用MS的脚本进行随机选取原子的操作，然后将选中的原子删除，即缺失原子。

(2)由于所选择的原子是随机的，因此为了保证结果的随机性，将随机选取原子的过程重复进行10次，即对缺失相同原子数的模型重复进行10次随机选择，并将选中的原子删除，即可得出10个缺失相同原子数的不同模型。由于篇幅所限，本文仅给出随机缺失5个原子的石墨烯模型中的3个模型示意图，如图18所示，对应的分子动力学模拟结果如图19所示。

图18 随机缺陷模型

图19 随机缺陷分子动力学模拟结果

(3)分别对这10个模型施加y方向和x方向的应力，并进行计算。

(4)将计算得出的应力应变值进行最小二乘法的直线拟合，得出10个杨氏模量的值后，取平均值即为最终的杨氏模量。随机缺陷石墨烯杨氏模量的误差棒如图20所示，根据误差棒图示，10个随机缺陷石墨烯模型的杨氏模量略有波动，相差并不大，锯齿型石墨烯杨氏模量的值在1 136～1 144 GPa波动，扶手型石墨烯杨氏模量的值在1 120～1 126 GPa波动。

图20 随机缺陷石墨烯杨氏模量的误差棒

图21为随机缺陷的缺失率和杨氏模量的关系图，从图21中可以看到，随着缺失率的增加，杨氏模量不断减小，并且锯齿型石墨烯的杨氏模量比扶手型的大。

图21 随机缺陷石墨烯的缺失率与杨氏模量的关系

4 结论

基于分子动力学方法，采用MS软件进行模拟，研究了不同类型含缺陷以及原子缺失率对石墨烯杨氏模量的影响。可得出以下结论。

(1)单空位缺陷的位置对石墨烯杨氏模量的影响，由缺陷对模型稳定性的影响决定。当影响较大时，边缘位置的缺陷对于模型稳定性相对于中间位置的缺陷更大，杨氏模量的值下降更多；反之，当影响较小时，边缘位置的缺陷对于模型稳定性相对于中间位置的缺陷更小，杨氏模量的值下降更少。

(2)对于映射长条状缺陷、映射圆孔状缺陷等不同形状缺陷的石墨烯，随着缺失率的增大，杨氏模量均减小。对于随机缺陷的石墨烯，杨氏模量也随着缺失率的增加而减小。

(3)对于映射圆孔状缺陷的石墨烯，锯齿型石墨烯的杨氏模量总大于扶手型石墨烯的杨氏模量。对于映射横向长条状缺陷和映射纵向长条状缺陷，随着缺失率的增大，锯齿型和扶手型的杨氏模量相差较大。当施加应力方向对含缺陷模型的稳定性影响较大时，其杨氏模量减小的幅度就越大，当施加应力方向对含缺陷模型的稳定性影响不大时，其杨氏模量减小的幅度就小。