基于EFEMD-HT能量法的电力系统低频振荡模态辨识
张程,邱炳林,刘佳静
(1. 福建工程学院电子电气与物理学院,福州350118;2. 智能电网仿真分析与综合控制福建省高校工程研究中心,福州350118)
0 引言
随着电网规模的持续扩大,各区域电网互联互通,使得当前电网的稳定运行能力下降,特别是基于电网的弱阻尼或欠阻尼等原因,使系统发生低频振荡现象[1 - 2],特别地,系统若以水电机组为主,还存在着发生超低频振荡的风险[3 - 5],振荡愈发频繁,严重时将导致系统运行解裂。抑制低频振荡的关键在于能够迅速准确地辨识出主导振荡模式的相关参数,较具代表性的一个分析方法为特征值分析法,由于新能源并网、电网规模持续扩大等原因[6 - 7],特征值分析法的计算越发复杂、计算速度较慢,其运用范围也在不断受限。
为实现电力系统的安全稳定运行,对电网进行实时的监测监控已成为当下电网安全稳定运行必不可少的环节,同步相量单元(synchronous phasor unit, PMU)的广泛配置及电力系统广域测量系统(wide area measurement system, WAMS)的广泛应用,使实测信号分析成为一大研究重点[8 - 9]。常用的信号分析法主要有快速傅立叶变换(fast Fourier transformation, FFT)[10]、自回归滑动平均模型(autoregressive moving average,ARMA)法[11 - 12]、小波变换(wavelet transform, WT)[13]、Prony[14 - 15]和希尔伯特-黄变换(Hilbert-Huang transformation, HHT)[16 - 17]等方法。文献[10]中的FFT法能够获取系统的频率但不能获得系统的阻尼,且传统的FFT法无法实现在线分析的功能;文献[11 - 12]中的ARMA模型法虽然能够计算出系统的阻尼系数和振荡频率,但在模型阶数的确定过程中,计算量大且较为复杂;文献[13]中的小波分析法存在小波脊选取困难的缺点;Prony分析法存在抗干扰能力较差,易受噪声影响的问题[14],基于此问题,文献[15]通过对Prony分析法进行改进,在一定程度上解决了抗噪能力不足的缺点,但若是在多种振荡模式共同作用下,其辨识振荡模式参数的精度不足等问题也随之而来。
近年来,由于HHT具有较强的自适应性能力、能够分解各种非线性信号等优势[16],其应用越发广泛,文献[17]中的HHT克服了传统FFT法和Prony法处理分析非平稳信号的不足与WT法小波脊选取困难等问题,但HHT法在EMD分解的过程中存在严重的端点效应,从而在分解的过程中存在较大的偏差,为此文献[18]通过建立极值点对称延拓的方法对算法进行了改进,虽有效解决了算法的端点效应但不可否认其模态混叠现象仍然存在。为解决模态混叠的问题,文献[19]通过引入信号能量法对EMD分解的IMF用半周期能量法进行计算并权重,从而筛选出信号的主导振荡模式分量,虽其结果有效可行,但因该方法只适用于二阶模型下的振荡信号应用范围有限。对此,文献[20]通过提出TEO能量指标并将其应用在语音信号上的处理,使能量法指标的应用不再局限于二阶模型下的信号。文献[21]将该方法与经验模态分解技术进行结合,基本能够确定出系统的主导振荡模式,但其获取模式阻尼比仍以二阶模型下的信号能量分析法为基础,所得到的结果存在一定的误差,且TEO指标存在抗噪性较差等不足而有待进一步完善[22]。
基于上述分析,本文提出经验模态分解的能量函数-希尔伯特变换(energy function of empirical mode decomposition-Hilbert transformation, EFEMD- HT)能量法,通过Hilbert变换与EFEMD能量法的结合,解决了EMD分解过后出现较多的分量而无法确定出系统的主导振荡模式及其对应的主导振荡参数。本文所提的EFEMD-HT能量法能够对EMD分解出的各分量进行能量计算并权重,从而筛选出系统的主导振荡模式,最后通过Hilbert变换对主导振荡模式进行参数的提取。通过对给定的理想信号、EPRI- 36机系统仿真信号以及电网实测PMU信号进行仿真验证,证实了本文所提EFEMD-HT能量法能够对系统的主导振荡模式进行准确的辨识。
1 EFEMD-HT的构成
1.1 EFEMD-HT能量法
对于信号能量的求取,目前可用方法较少,其中,信号能量法是根据发电机受扰轨迹分析系统动态特征的一种方法,主要原理是基于阻尼耗散能量原理[23],该方法以物理模型为基础。鉴于此,本文将从物理过程中提出EFEMD能量法。
用单位质量为m的质点和一条弹性系数为k的弹簧,一端固定而另一端与质点相连,将质点向固定点挤压后松手,续而发生振荡;则小球在t时刻的位移表示为:
(1)
式中:A为振幅;φ0为初始相位,在理想振荡条件下,其能量总和为小球的动能和弹簧的势能之和,表示为:
(2)
其中,小球的瞬时速度用微分表示,即
(3)
将式(1)、式(3)代入式(2),可得:
(4)
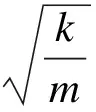
E∝A2f2
(5)
若将该分析结果迁移到一个连续的振荡信号系统中,则式(1)的表达式为:
xn=Acos(αn+φ0)
(6)
式中:α=2πf/fs;f为振荡频率;fs为采样频率[24]。
低频振荡信号通常是含有噪声的信号,每个采样点的能量值易受噪声的影响,为提高计算过程中对每个采样点能量的准确求取,本文将根据文献[22]中取相隔a个采样点进行9点3组方程采样方法,具体过程如下。
(7)
(8)
(9)
对其进行三角变换,且当α非常小时,即采样频率足够大时,对sin2(α)进行泰勒级数展开,可得sin2(α)≈α2, 即有:
(10)
由式(5)和式(10)可得,在某一采样点xn处,其EFEMD-HT能量值记为:
(11)
通过计算出信号的每个采样点所具有的相对能量值,对各个采样点的能量求总和,即可获得所对应的IMF所具有的相对能量值,并对它们进行能量占比分析,如式(12)所示。
(12)
式中:m为采样点总数;Ex为某一个IMF所具有的相对能量值。
(13)

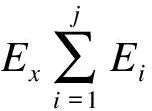
(14)
由于经验模态分解(EMD)是根据被处理信号自身所具有的时间尺度作为依据,将被分解信号分解成不同频率尺度的IMF[25 - 26],此时虚假分量和主导分量将同时产生,因而本节的目的在于应用EFEMD-HT能量法计算出各IMF的能量权重与对比值ρ, 从而筛选出主导振荡模式,剔除EMD分解分量中存在的虚假分量。
1.2 Hilbert变换解析IMF
通过1.1节引入的EFEMD能量法剔除虚假无关分量,再用Hilbert变换法对筛选出的主导振荡模式提取振荡频率、阻尼比等关键参数,首先定义IMF为x(t), 再由x(t)、y(t)构成的共轭复数对,得到解析信号z(t)、 瞬时幅值A(t)、 瞬时相位φ(t)以及瞬时频率f(t):
z(t)=x(t)+jy(t)=A(t)ejφ(t)
(15)
(16)
(17)
由式(16)和(17)可得f(t)的表达式为:
(18)
各振荡模式的瞬时阻尼比ξ(t)的表达式如式(19)所示。
(19)
详细的推导过程在文献[27]中已给出,本文不再推导;衰减因子λ的表达式如式(20)所示,其中ω为角频率,ξ为阻尼比。
(20)
通过Hilbert变换,获取各振荡模式瞬时参数的均值,从而得到各主导的振荡频率、阻尼比等参数。
2 基于能量法对振荡模态参数的辨识
本文所提基于EFEMD-HT能量法的低频振荡模式辨识步骤归纳如下:
1)首先找出信号的局部极值点,用包络线围住上、下极值点,从而得到上、下包络线,取其均值,记为m1,再用原信号x(t)减去m1得到h1,若满足条件,则h1为第一个IMF;若h1不满足条件,则将h1作为原信号重复上述操作;
2)当h1满足条件时,则进行第二个IMF的分解,用x(t)减去h1,作为新的信号r1继续分解,重复上述操作,直至最后一个信号rn成单调函数,不能继续再作分解,从而得到n个IMF模态分量和一个剩余分量rn;
3)通过对原始信号的分解,获得n个IMF分量,随后由式(11)计算出每一个IMF分量中的每一个采样点所具有的相对能量值K(xn), 并根据式(12)将各采样点的相对能量值进行求和,从而得到每个分量各自的相对能量值的总和Ex;
4)由EFEMD能量法计算得到的各个IMF分量所具有的能量值之后,分别采用式(13)—(14)对每一个IMF分解分量进行能量权重分析ηx与对比值ρ的计算,并将其从大至小排序,且根据预先设定的值,通常将能量权重大于15%的IMF分量筛选出来作为系统的主导振荡模式;
5)通过以上步骤确定出主导振荡模式并对其进行Hilbert变换,根据式(18)—(20)对瞬时参数求取均值获取信号的主导频率、衰减因子和阻尼比等参数信息。具体辨识流程如图1所示。
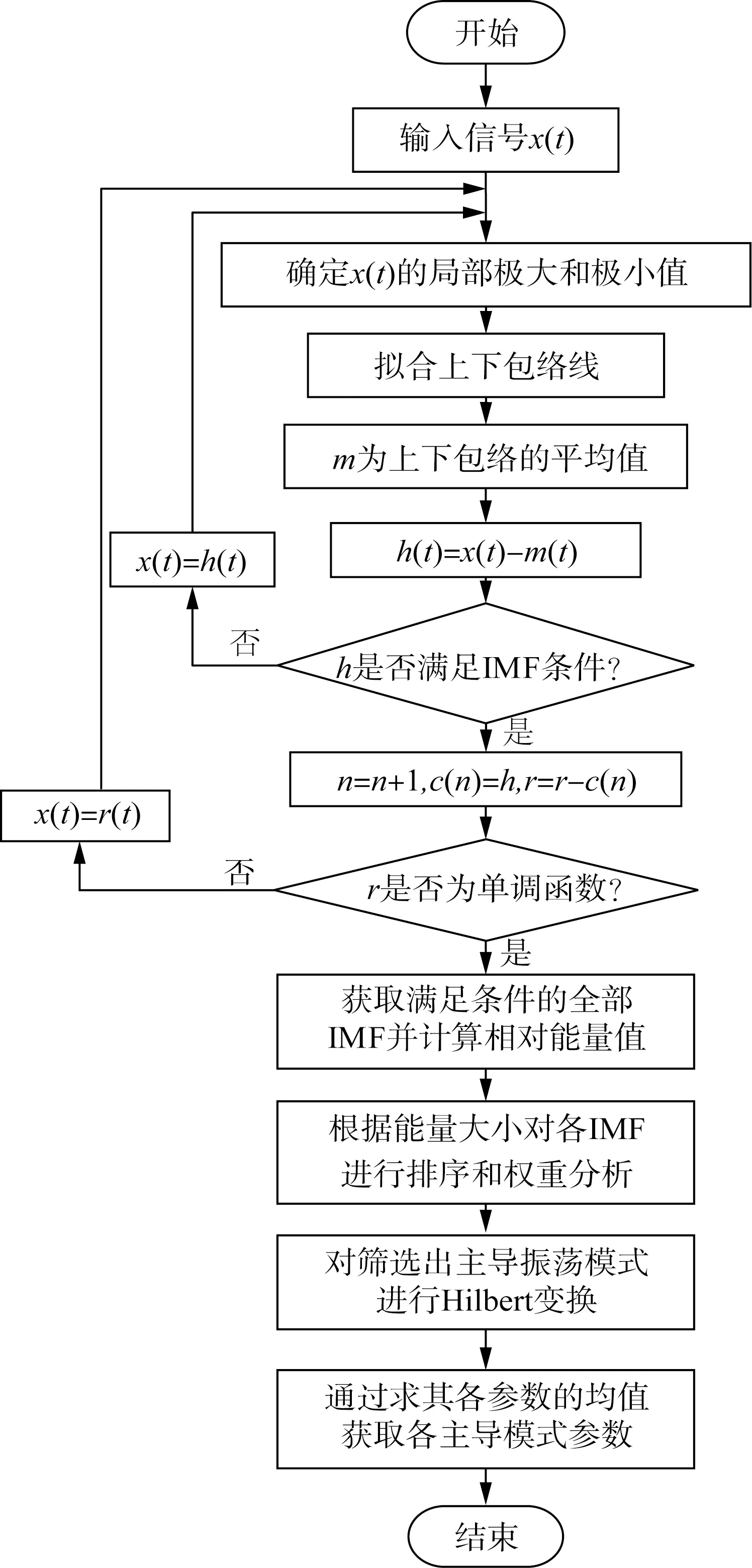
图1 本文提出的能量法提取参数的总流程Fig.1 General process of extracting parameters of energy method presented by this paper
3 仿真与实验分析
3.1 测试信号
实际的电力系统低频振荡信号通常是含噪信号,现构造低频振荡信号如下,由两个正弦信号和噪声信号构成:

(21)
测试信号由频率为0.5 Hz、1 Hz以及均值为0、方差为0.2的白噪声信号w(t)构成的复合信号,信号的采样频率为35 Hz,采样点数为800,得到的含噪信号原始信号波形图如图2所示。
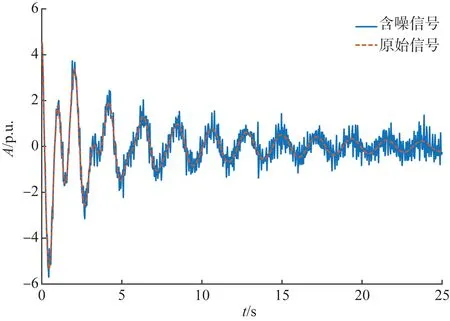
图2 含噪信号及原始信号Fig.2 Signal containing noisy signal and original signal
首先,对含噪信号进行EMD分解。本文截取EMD分解的部分结果图,如图3所示,从图3中可知IMF1分量中含有大量噪声,初步判断IMF1为虚假无关分量,但人为的判断无法保证判断的准确性,而传统分析方法亦是如此,如图4所示,通过对各IMF进行Hilbert变换,获取相应的瞬时频率图,只需对各分量的瞬时频率求取均值,即可得到IMF各自的频率值。
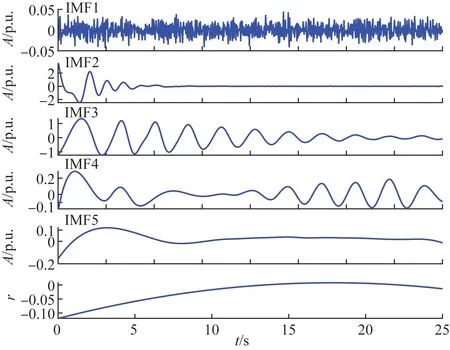
图3 EMD分解的部分结果Fig.3 Partial results of EMD decomposition
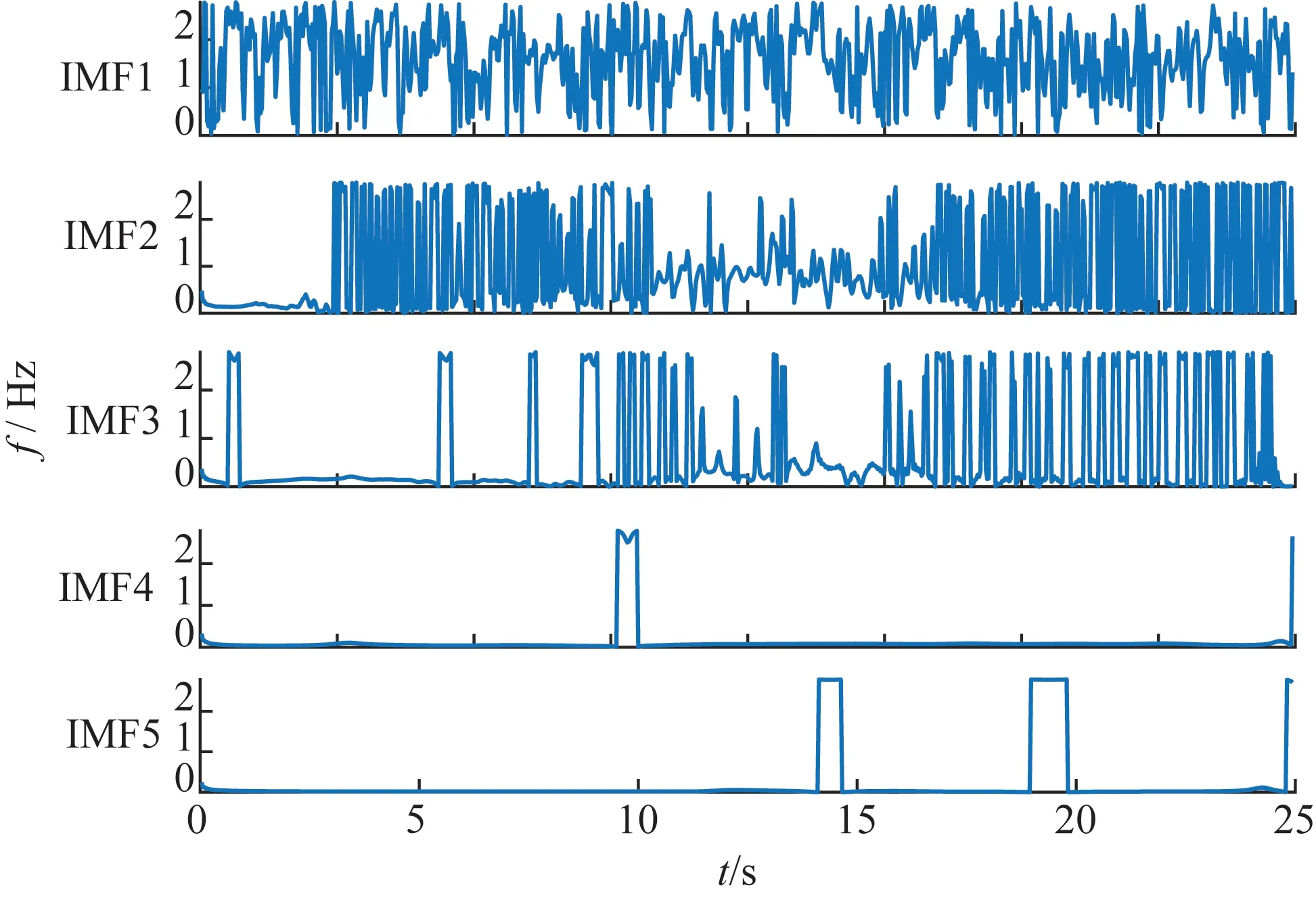
图4 部分IMF的瞬时频率图Fig.4 Instantaneous frequency diagram of IMF
其次,对主导振荡模式分量和虚假分量加以筛选区分。本文使用EFEMD-HT能量法指标进行筛选。首先计算出各IMF分量的相对能量值,结果如图5所示,根据能量值的大小可初步判断振荡信号中含有两个主导振荡模式IMF1和IMF2。为验证上述结论,通过对各分量进行Hilbert变换,由频谱图可知,主导振荡频率为0.5 Hz和1 Hz左右,即验证了有两个主导振荡模式。为验证主导振荡模式为IMF2和IMF3,需要对各IMF分量进行能量权重,并进行相对值ρ的计算,其结果如表1所示,能量权重值η和相对能量值ρ较大的为IMF2和IMF3。

图5 各个IMF的量值Fig.5 Energy value of each IMF
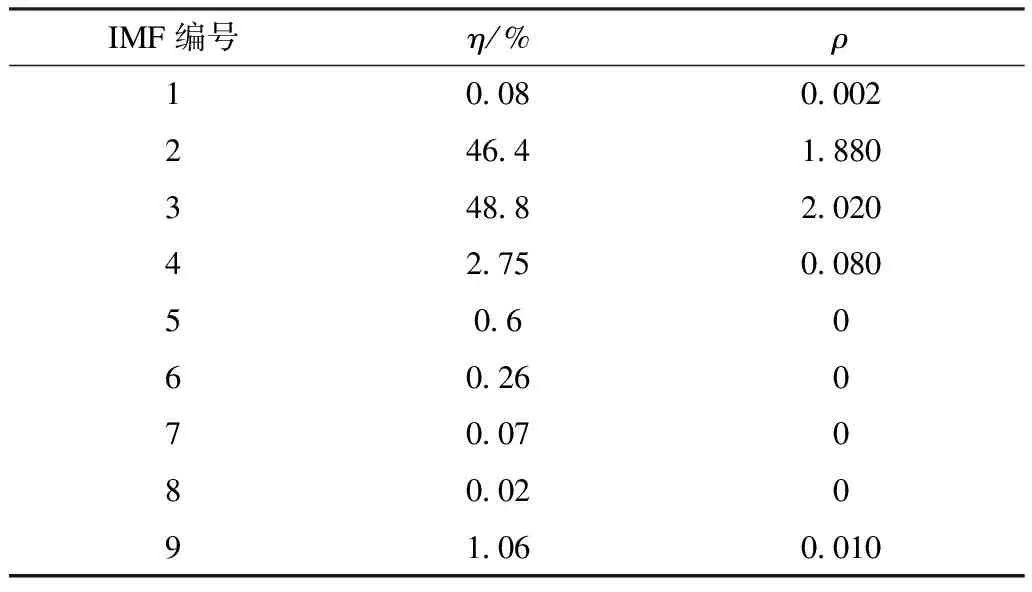
表1 各个IMF的能量权重及对比值的结果Tab.1 Energy weights of each IMF and the results of the ratios
本文在程序上,先对EMD分解出的各分量按顺序进行编号并排序,通过EFEMD能量法计算出各IMF分量的能量值,并对相应顺序上的分量进行能量权重以及相对值计算,从而获得相应的数组,利用判断加循环的操作,将数组中权重值大于15%的分量作为系统的主导振荡模式,以此确定出本文的主导振荡模式。随后利用Hilbert变换对本文筛选出的两个主导振荡模式进行参数的提取,计算出相应的频率、阻尼比等参数信息。
为验证本文分析方法提取参数的有效可行性,以下采用3种不同分析方法对实际辨识出的参数值与给定信号的参数值进行对比分析,如表2所示,其中测试信号的频率为0.5 Hz和1 Hz、阻尼比为3.18%和7.9%。首先对于HHT而言,本文的EFEMD-HT能量法与HHT分析法本身都是对瞬时参数求取均值,所以两种分析法都会因为每次不同的运行结果而在数值上稍有偏差,但两种方法的根本区别在于HHT是对每一个EMD分解的结果进行解析,本身是没有能力能够从诸多参数中识别出主导振荡的参数,表中的HHT辨识结果是人为筛选的,而本文分析方法是通过能量指标自行筛选;其次,就辨识精度而言,EFEMD-HT能量法也略优于传统的HHT法,原因在于本文的分析方法在算法的处理上,较大程度避免了噪声干扰以及虚假分量的影响;另外,在体现避免噪声影响的重要性方面,与本文方法相比较,Prony法的参数辨识精度明显较低,特别是其阻尼比的误差明显较大。
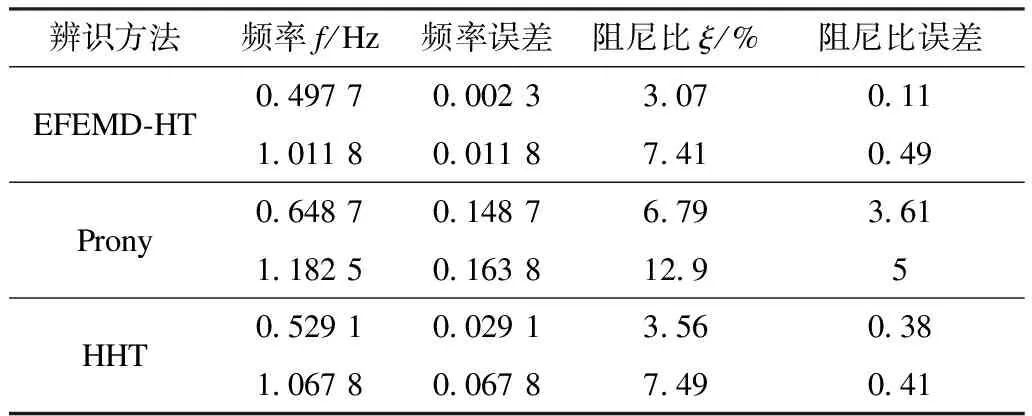
表2 主导振荡模式参数提取的误差分析Tab.2 Error analysis of parameter extraction of dominant oscillation mode
3.2 EPRI- 36系统仿真算例
为了验证本文所提出的方法在电力系统低频振荡模态辨识分析中的有效性,采用EPRI- 36系统如图6作为本文仿真分析系统。在母线20处设置一维持0.4 s,大小为0.5 p.u.的冲击负荷。以1号发电机的有功功率作为输入,由于本算例的故障为特别小的系统干扰,所以人工加入信噪比为25 dB的白噪声来模拟电力系统实际采样信号,其信号干扰已非常明显,如图7所示。利用电力系统综合分析程序小干扰稳定分析模块计算得到EPRI- 36节点系统G1机电振荡模式特征值,如表3所示。

图6 EPRI- 36节点仿真系统Fig.6 IEEE- 68 Node simulation system
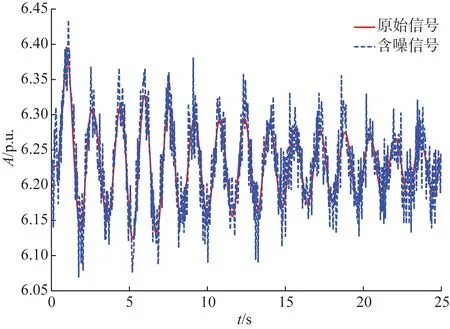
图7 G1有功功率的原始信号和含噪信号Fig.7 Original signal and noisy signal of G1 active power

表3 有功功率振荡信号的特征值分析结果Tab.3 Eigenvalue analysis results of G1 active power oscillation signal
G1有功功率的原始输入信号曲线和人为加入噪声后的信号曲线如图7所示。首先,对有功功率的原始输入信号进行小干扰分析,从表3中可知,模式1的阻尼比较大,具有较强的阻尼特性,能够有效地抑制振荡,而其他模式的阻尼比均小于10,阻尼特性较弱,需要后续人为采取相应的措施来抑制振荡所带来的系统失稳风险。
首先,对加入噪声后的G1有功功率信号进行EMD分解,部分分解结果如图8所示。可知IMF1和IMF2分量中含有大量噪声,初步判断这两个分量为虚假无关分量。接着使用EFEMD-HT能量法对各IMF分量进行能量值计算,其计算结果如图9所示。根据能量值的大小可知系统中存在两个主导振荡模式,随后对各IMF分量进行Hilbert变换,如图10所示。确定系统确实存在两个主导模式,振荡频率在0.75 Hz和1.8 Hz左右,最后通过能量权重和相对值计算,如表4所示,确定系统的主导振荡模式为IMF3和IMF4。
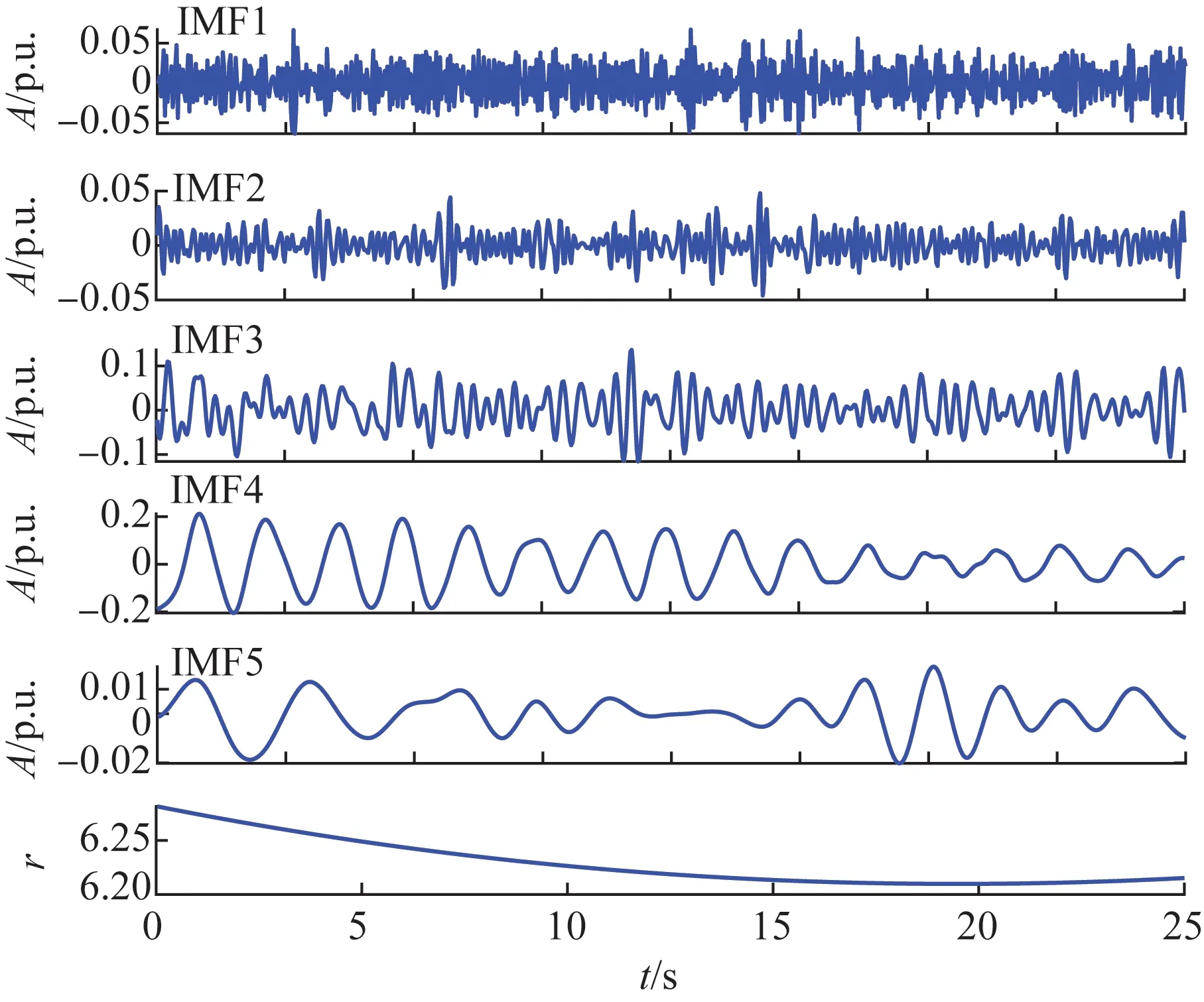
图8 EMD分解的部分结果Fig.8 Partial results of EMD decomposition
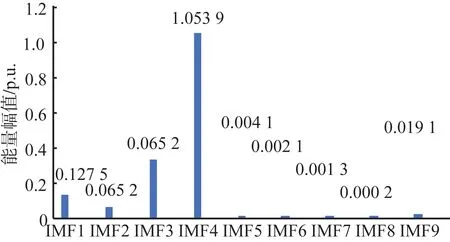
图9 各个IMF的能量值Fig.9 Energy values of all the IMFs

表4 各个IMF的能量权重及对比值的结果Tab.4 Energy weights of each IMF and the results of the ratios
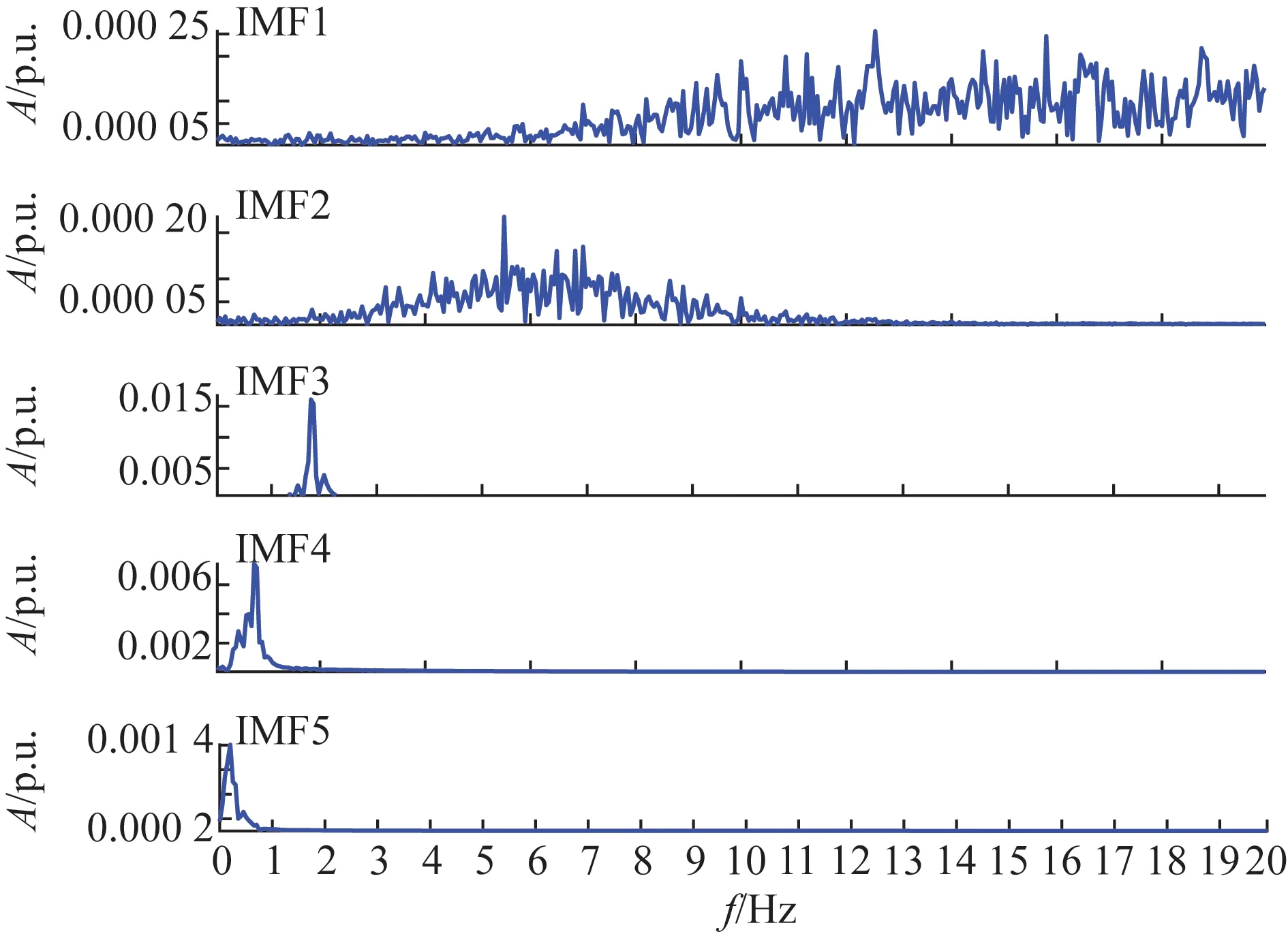
图10 部分IMF的频谱图Fig.10 Spectrum of a part of IMF
随后对筛选出的主导振荡模式IMF3和IMF4进行Hilbert变换,得到如图10所示的IMF频谱图。在相应的时间内对瞬时频率取均值,得到频率、阻尼比等参数信息,如图11所示。其中由IMF3和IMF4可对应特征值分析结果中的模式2和模式7,频率分别为1.825 6 Hz、0.784 1 Hz,阻尼比分别为6.874 7%、0.986 1%;通过表5中的3种分析方法辨识出的实际参数值,与特征值分析结果得出的参考值进行对比,分析其误差并对IMF3和IMF4 进行重构,与原始信号曲线进行对比,如图12所示。
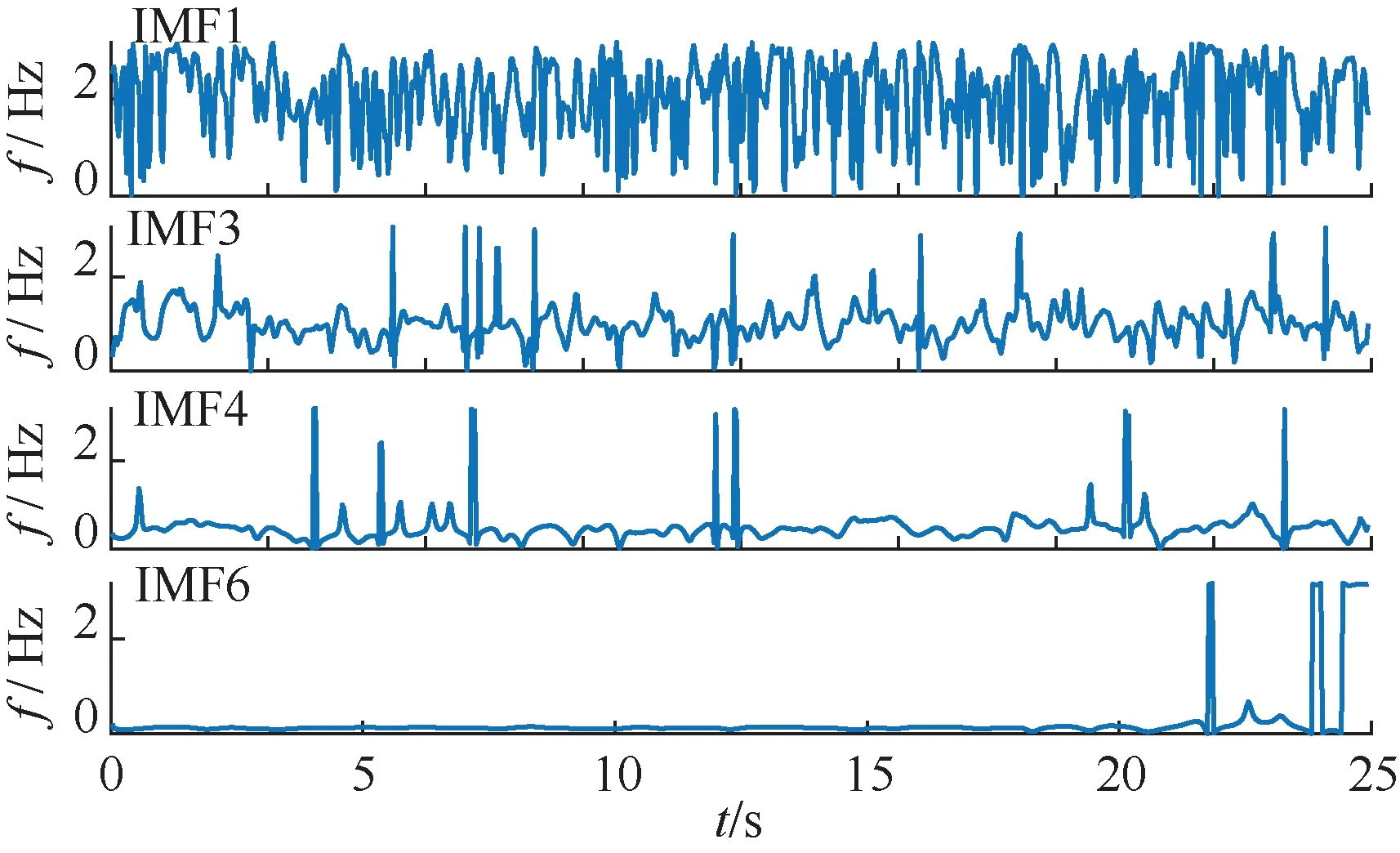
图11 部分IMF的瞬时频率图Fig.11 Instantaneous frequency diagram of a part of IMF

图12 重构信号和原始信号的比较Fig.12 Comparison of the reconstructed signal and the original signal
从图12可知,筛选重构后的信号基本能够还原出原始信号;3.1节测试信号和本节仿真信号的分析结果表明,使用EFEMD-HT能量法能够较好地对含噪信号进行分解、筛选、重构、参数提取,其辨识精度也能较好地满足要求。表5为本文方法与HHT、Prony等传统参数辨识法的对比,通过表5可直观地体现出本文方法的有效性、准确性。
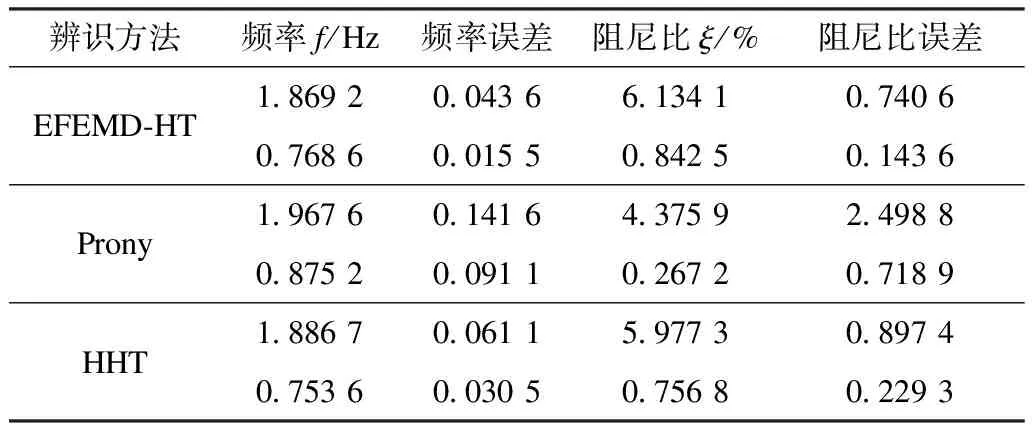
表5 主导振荡模式的误差分析Tab.5 Errors analysis of dominant oscillation mode
针对HHT方法辨识振荡模式不准确的问题,大多数的研究方向都是通过对HHT本身的端点延拓以及包络插值等方面进行改进,或是通过更好的去噪环节对含噪信号进行预处理,以提升最终振荡模式的辨识精度,但这些方法都未解决HHT一个最为关键的问题,即如何从EMD分解出的众多分量中确定出系统的主导振荡模式;本文方法的提出有效地解决了主导振荡模式难以确定的问题,能够在前人对HHT算法改进的基础上再对本文方法进行一个应用,以进一步提升主导振荡模式的辨识精度。
4 实测电网数据
为进一步验证本文所提出的方法在实际电网中的可行性,选取一段电网实测的低频振荡故障信号作为分析目标,该事故于2007年10月发生在美国的宾西法尼亚州,电网实测频率数据曲线如图13所示,数据记录长度为35 s。
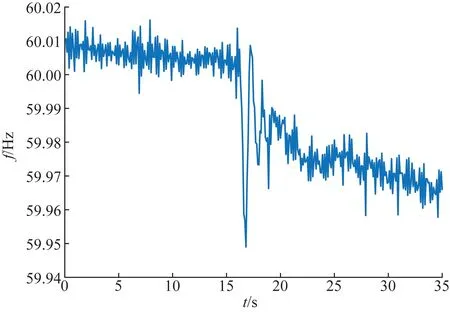
图13 电网中的实测频率曲线Fig.13 Measured frequency curve in power grid
由图13可知,在频率信号的中段区域内系统明显受到了外界干扰,初步判断该段为低频振荡发生的有效区间段,在信号参数的辨识过程中也主要是对该数据段进行波形分析以获得系统的主导振荡模式。
如图14为实测信号的小波时频分析图,由图中各频率分量颜色的冷暖可以确定出系统发生低频振荡的时间大概在15~20 s,所发生的振荡频率介于1.5~2 Hz左右。
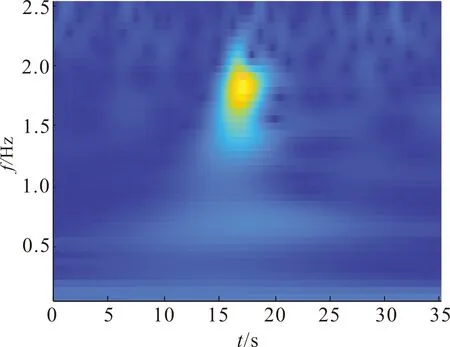
图14 小波时频分析图Fig.14 Wavelet time-frequency analysis diagram
首先,将上述低频振荡频率数据进行EMD分解,所得分解结果波形如图15所示;随后对各IMF分量能量值进行计算,所得结果分别为0.015 3、0.043 6、0.057 2、0.010 4、0.000 8、0.000 3,并根据本文提出的筛选指标确定出系统的主导振荡模式,即进行能量权重分析以此确定出系统的主导振荡模式分别为IMF2和IMF3。

图15 EMD分解的部分结果Fig.15 Partial results of EMD decomposition
最后得到的分析结果如下:系统存在两个主导振荡模式,其频率分别为1.731 5 Hz、1.826 4 Hz,阻尼比分别为0.018 2和0.007 4。综上分析,表明了本文EFEMD-HT能量法在实测信号分析中的有效性与可行性。
5 结论
在当今电网规模的持续扩大以及当代新能源技术的发展与新能源并网的背景下,其低频振荡造成的系统失稳风险可能发展成整个大电网的安全稳定运行风险,为此,辨识出系统的低频振荡模式、提取振荡中的关键参数尤为重要,为后续如何抑制低频振荡提供可靠的数据支持与理论支撑。
本文通过EFEMD-HT能量法,利用EMD技术先将信号进行分解,分解出的各振荡模式进行能量计算并权重,并通过相对值计算进行验证主导振荡模式的筛选是否正确,对筛选出的主导振荡模式进行重构从而还原出原始信号。
通过Hilbert变换获取主导振荡模式的各参数,对辨识出的关键振荡模式参数信息进行对比分析,验证了本文EFEMD-HT能量法能够较好地实现主导振荡模式参数的提取,其辨识参数的误差也在可接受的范围内,最后通过电网实测PMU数据进一步验证了该方法在实际中的可行性。

