兼顾经济性和多阶段抗灾性能的骨干网架多目标规划方法

娄源媛，陈昌铭，刘新苗，龚贤夫，陈鸿琳，林振智

(1. 广东电网有限责任公司，广州510600；2. 浙江大学电气工程学院，杭州310027；3. 广东电网有限责任公司电网规划研究中心，广州510080)

0 引言

近年来，台风、冰灾等极端自然灾害严重威胁着电力系统的安全稳定运行。例如，2015年台风“彩虹”造成广东湛江电网大停电[1]；2017年台风“天鸽”造成珠海电网对澳供电停电51 min[2]；2019年英国伦敦一段输电线路受到雷击跳线，导致110万用户被迫停电[3]。因此，有必要研究具备抗灾性能的骨干网架，以减少极端自然灾害对电力系统造成的破坏和损失。

筛选骨干网架需要基于多种指标，如节点线路重要度、网架抗灾性能等。在节点线路重要度指标方面，文献[4]在传统电气介数的基础上结合了线路关键度评价指标，提出能够兼顾电网脆弱性及线路关键度的综合电气介数。文献[5]运用熵权法对节点和线路各重要度评估指标进行客观赋权。文献[6]建立了考虑线路和节点重要度的骨干网架规划模型，并采用离散粒子群算法对模型进行求解。文献[7]在电网节点、线路重要度评估基础上，基于图论算法给出了一种电网核心骨干网架构建方法。在网架抗灾性能指标方面，文献[8 - 9]均从抗毁性、可恢复性、连通性三个方面构建生存性指标体系，并以生存性指标最大为目标函数构建骨干网架规划模型，采用改进生物地理学优化算法进行求解。文献[10]从自然环境条件、电网结构强度和设备抗冰水平3个维度设计了抗冰骨干网架综合评价指标体系，并根据该抗冰指标体系筛选出抗冰骨干网架。文献[11]对现有电网结构中存在的防风抗灾薄弱环节进行分析，并据此给出防风骨干网架规划方法。文献[12]计及骨干网架的网架特性和电气特性，从可抵抗性、可恢复性、安全性和连通性4个方面分别构建了骨干网架的生存性指标体系，并采用线性判别分析与主成分分析相结合的方法对骨干网架的规划方案进行生存性评估。文献[13]提出一种基于系统生存性的骨干网架搜索方法，从系统可抗性、运行状态波动性和灾后可恢复性三方面建立生存性综合指标作为骨干网架综合抗灾能力的评估标准。

上述文献为骨干网架规划研究做出了重要贡献，但是它们构建的均为单目标函数，无法全面评估骨干网架的抗灾性能。为此，文献[1]以最大化经济性、系统可恢复性和网络抗毁性为多目标构建抗灾型骨干网架多目标规划模型，并引入图论修复策略对骨干网架拓扑进行修复。文献[3]提出以网架生存性、抗毁性和系统可恢复性为多目标的抗灾型骨干网架的优化模型，以提高骨干网架在灾害各阶段的抗灾性能，同时运用图论修复策略加速骨干网架拓扑的生成。文献[14]基于支路和节点重要度指标，并引入网络整体抗毁性指标，构建了考虑元件重要度和网络抗毁性的骨干网架多目标规划模型。然而，上述文献考虑的多目标函数不够全面，例如文献[3]并未考虑骨干网架规划的经济性，文献[1]忽略了骨干网架生存性，文献[14]则同时忽略了骨干网架规划经济性、生存性和可恢复性。要得到各方面性能均衡的骨干网架规划结果，需要兼顾经济性和多阶段抗灾性能。

在多目标优化模型求解方面，非支配排序遗传算法(non-dominated sorting genetic algorithm, NSGA)是在遗传算法的基础上进行改进的一种智能算法，相比传统的遗传算法，具有求解速度快、解集收敛性好等优点，是现代多目标求解算法的典型算法之一。然而，NSGA具有非支配排序的高计算复杂性、缺少精英策略等缺点。因此，改进的非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)引入了精英策略、拥挤度估计策略和快速非支配排序策略来对传统的NSGA进行改进，其在收敛性、均匀度等方面相比NSGA具有优势[14 - 15]。

针对现有研究的不足，本文提出一种兼顾经济性和多阶段抗灾性能的骨干网架多目标规划方法。首先，以骨干网架规划的经济性、生存性、抗毁性及可恢复性为多目标函数，构建骨干网架多目标规划模型；然后，运用嵌入图论修复策略的改进非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)对模型求解，得到骨干网架规划策略的Pareto最优解集；接着，运用熵权法筛选出骨干网架规划策略的Pareto最优折中解；最后，以某区域实际输电网为算例来验证本文所提模型的有效性。

1 兼顾经济性和多阶段抗灾性能的骨干网架多目标规划模型

1.1 骨干网架多目标规划模型的目标函数

为兼顾骨干网架规划的经济性和多阶段抗灾性能，本文以最大化骨干网架规划经济性、生存性、抗毁性以及可恢复性为多目标函数。其中，生存性、抗毁性和可恢复性分别反映灾害来临时、灾害持续阶段以及灾害结束时的骨干网架抗灾性能。

1.1.1 最大化骨干网架规划经济性

骨干网架规划所需的费用为节点加固费用和线路加固费用。因此，本文定义骨干网架规划经济性目标函数feco为骨干网架节点和线路加固费用的倒数：

(1)

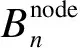
1.1.2 最大化骨干网架生存性

骨干网架生存性好坏的评价标准为：在台风等极端天气情况下，骨干网架中能够保障的重要电力用户供电量[3]。因此，本文定义骨干网架生存性目标函数fsur为骨干网架在自然灾害下的负荷保障度。

(2)

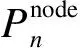
1.1.3 最大化骨干网架抗毁性

骨干网架抗毁性的优劣可以通过台风等极端天气情况下骨干网架维持稳定运行和抵抗连锁故障的能力来反映[16 - 17]。骨干网架连通度指标Icon定义为骨干网架的任意节点被毁坏后，剩余骨干网架中仍连通的节点对的平均值与原骨干网架的连通节点对的比值，能够有效反映骨干网架的抗毁性[18]。因此，本文将骨干网架连通度指标作为抗毁性目标函数fdes。

(3)

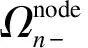
1.1.4 最大化电力系统可恢复性

电力系统可恢复性的好坏可以通过灾后骨干网架为全网恢复供电的效率来反映：网架覆盖率越高，说明骨干网架保留的重要节点和线路越多，且与未恢复节点的距离越近，则电力系统的可恢复性越强。因此，本文将骨干网架覆盖度指标[19]作为骨干网架可恢复性目标函数frec：

(4)

(5)

(6)

(7)

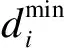
1.2 骨干网架多目标规划模型的约束条件

本文所提骨干网架多目标规划模型的约束条件包括网络连通性约束、重要节点线路保留约束以及潮流约束。

1.2.1 网络连通性约束

骨干网架中不应包含孤岛，所有节点均需有支路进行连通。因此，骨干网架的网络连通性约束可以通过式(8)表示。

(8)

式中Ωline为骨干网架支路集合。

1.2.2 重要节点、支路保留约束

电力系统中存在部分高重要性的节点和支路，例如医院、变电站、500 kV线路等，这些重要节点和支路需要保障其持续供电，如式(9)—(10)所示：

(9)

(10)

Buckling Impact Analysis of Cylinderial Shells with Opening and Reinforcement Under Axial Compression HU Fuquan,LI Pengfei,HE Zheng(60)

1.2.3 潮流约束

为了保证电力系统安全稳定运行，骨干网架需要满足潮流约束[21 - 22]，如式(11)—(14)所示：

(11)

(12)

(13)

(14)

2 基于嵌入图论修复策略的NSGA-Ⅱ算法的骨干网架Pareto最优解集求解方法

本文运用NSGA-Ⅱ对所提骨干网架多目标规划模型进行求解，可以得到骨干网架Pareto最优解集[23]。由于NSGA-Ⅱ新生成的子代种群具有随机性，会出现较多不满足式(8)所示的网络连通性约束的子代，若采用罚函数等方法淘汰劣子代，会影响算法的寻优效率。因此，本文采用基于广度优先搜索算法的图论修复策略[24]来修复不满足骨干网架网络连通性约束的子代基因，修复步骤如下。

步骤1：输入电力系统拓扑，根据拓扑求得电力系统邻接矩阵Wgrid；以支路电抗为权重求得电力系统加权邻接矩阵Wgrid,w；根据Wgrid和Wgrid,w求得电力系统节点对间的最短电气距离矩阵Wgrid,d以及最短电气距离对应的最短路径矩阵Wgrid,p。

步骤2：输入重要节点矩阵、重要支路矩阵以及当前的子代基因，确定当前的骨干网架拓扑；根据骨干网架拓扑求得骨干网架邻接矩阵Wbone和骨干网架节点对间的最短电气距离矩阵Wbone,d。

步骤3：运用广度优先搜索算法对骨干网架进行搜索，求得骨干网架的连通片矩阵Wbone,ltp；根据Wbone,ltp对电力系统加权邻接矩阵Wgrid,w进行修改，将连通片内的节点对间的最短电气距离置0。

步骤4：删除Wbone,ltp中只包含1个节点的连通片；运用弗洛伊德算法[1]求得各个连通片之间的最短电气距离矩阵Wbone,ltp,d。

步骤5：将Wbone,ltp,d作为权重，运用克鲁斯卡尔算法求得所有连通片之间的最小生成树。

步骤6：根据最小生成树对骨干网架进行修复，即对于任意两个相连的连通片，根据Wgrid,d和Wgrid,p选择两个连通片间最短电气距离最小的节点对作为修复路径的首末节点，其对应的最短路径作为修复路径。

基于前述的图论修复策略，本文提出一种嵌入图论修复策略的NSGA-Ⅱ算法，该算法的求解流程如图1所示。

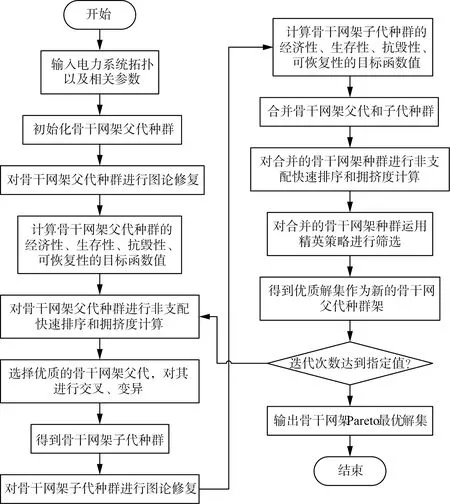
图1 嵌入图论修复策略的NSGA-Ⅱ算法流程图Fig.1 Flow chart of NSGA-Ⅱ embedded graph theory restoration strategy

3 基于熵权法的骨干网架Pareto最优折中解筛选方法

通过嵌入图论修复策略的改进NSGA-Ⅱ算法可以得到骨干网架的Pareto最优解集。然而，解集中的解的多目标函数值往往无法同时达到最优，因此工作人员需要权衡各方面的因素进行综合考虑，在求得的骨干网架Pareto最优解集中筛选出最合适的骨干网架规划方案，即Pareto最优折中解。常用的选取Pareto最优折中解的方法有线性加权法、模糊推理法、层次分析法等方法，但是这些方法在确定各目标函数的权重系数时易受决策者偏好的影响。熵权法是一种通过信息熵理论确定系统中各项指标赋权大小的方法。相较于线性加权法、模糊推理法、层次分析法等主观赋权法，熵权法作为客观赋权法能更好地避免主观因素的影响，从而提高分析的可信度和精确度。为此，本文采用熵权法来求取骨干网架规划的多目标函数的权重系数，具体步骤如下所示。

步骤1：由于骨干网架规划模型各个目标函数的量纲不同，因此在筛选出骨干网架的Pareto最优折中解之前，需要对骨干网架的Pareto最优解集中所有解的多个目标函数值进行线性标准化处理[25]。目标函数可以分为效益类目标函数和成本类目标函数，其中效益类目标函数值越大越好，成本类目标函数值越小越好。根据目标函数类别的不同，效益类和成本类目标函数的线性标准化处理公式也不同，如式(15)所示。

(15)

步骤2：计算骨干网架规划模型各个目标函数的熵权系数。熵能够反映同一目标函数的不同解之间的差距情况。针对具有M个目标函数和它们对应的N个解的Pareto最优解集，第i个目标函数的熵Si可通过式(16)求得。

(16)

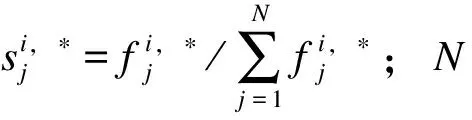
求得第i个目标函数的熵之后，即可通过式(17)求出第i个目标函数的熵权系数Wi。

(17)

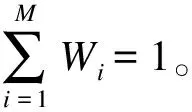
步骤3：计算每个Pareto解的综合指标，根据综合指标选取最优解。第j个解的综合指标Zj可由式(18)求得。

(18)

求得骨干网架Pareto最优解集的所有解的综合指标后，筛选出的综合指标最大的解即为骨干网架的Pareto最优折中解。

4 算例分析

本文以某区域实际输电网为算例对所提骨干网架多目标规划模型的有效性进行验证。该输电网共有125个节点(9个500 kV节点，40个220 kV非发电机节点、12个220 kV发电机节点和64个110 kV节点)和155条线路，其拓扑图如图2所示。根据式(6)和式(7)求得的输电网节点和线路重要度归一化指标如图3所示。由图3可知，辨识出的重要节点和线路(即归一化重要度指标大于0.5)包括全部500 kV节点和线路以及大部分220 kV节点和线路，这也与实际中电压等级越高的节点和线路越重要这一常识相符合。

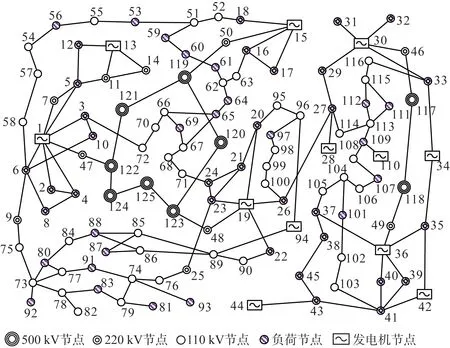
图2 某区域实际输电网拓扑图Fig.2 Topology of an actual regional transmission network

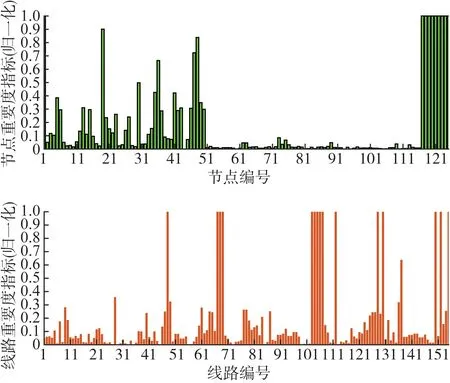
图3 输电网节点和线路重要度指标Fig.3 Importance index of nodes and lines in transmission network

通过嵌入图论修复策略的NSGA-Ⅱ算法求得骨干网架的Pareto最优解集，再根据熵权法求出经济性、生存性、抗毁性和可恢复性4个目标函数的权重依次为0.27、0.45、0.17和0.11。基于各目标函数的权重对骨干网架Pareto最优解集进行筛选，得到骨干网架加固策略的Pareto最优折中解如图4所示。图4所示的骨干网架加固策略和全网加固策略的对比如表1所示。

结合图4和表1可知，所有500 kV节点和92%的发电机节点均包含在图4所示的骨干网架加固策略中，因为这些节点在输电网受到灾害损坏的情况下是实现电力系统恢复的重要一环。将骨干网架的生存性、抗毁性和可恢复性指标除以Pareto最优解集中各指标的最大值进行归一化，从而得到图4所示的骨干网架加固策略的生存性、抗毁性和可恢复性归一化指标分别为0.90、0.95和0.89，可见该最优折中解具有较高的多阶段抗灾性能。此外，由表1可知，图4所示的骨干网架加固策略仅需加固121条线路和115个节点，加固费用仅为1 902.6万元，相比全网加固策略分别少加固34条线路和10个节点，节省了20.5%的投资成本，具有更好的经济性。

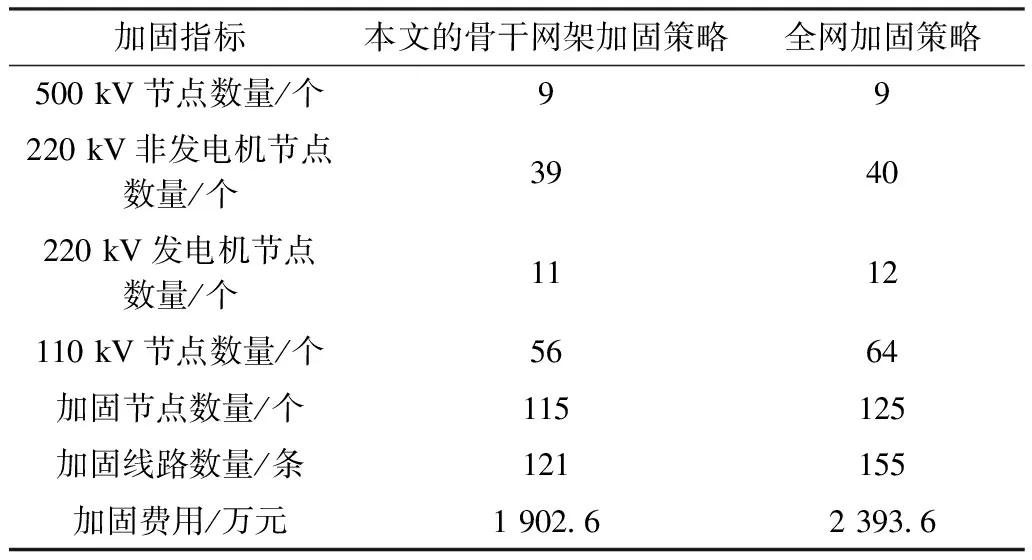
表1 本文的骨干网架加固策略和全网加固策略的对比Tab.1 Comparison of backbone grid reinforcement strategy obtained by the proposed model and whole grid reinforcement strategy

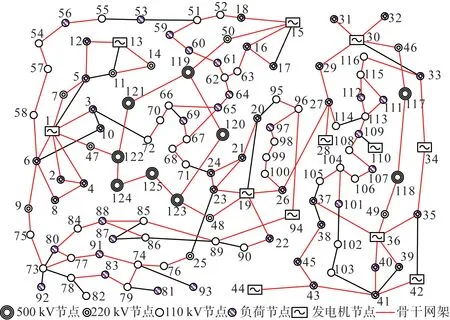
图4 骨干网架的Pareto最优折中解Fig.4 Pareto optimal compromise solution of backbone grid

为了更好地验证本文所提骨干网架多目标规划模型的有效性，将本文所提骨干网架多目标规划模型(M-MO)与经济性最优规划模型(M-ECO)、生存性最优规划模型(M-SUR)、抗毁性最优规划模型(M-DES)、可恢复性最优规划模型(M-REC)所求得的骨干网架规划方案在归一化后的经济性、生存性、抗毁性、可恢复性4个方面进行对比，结果如表2所示。

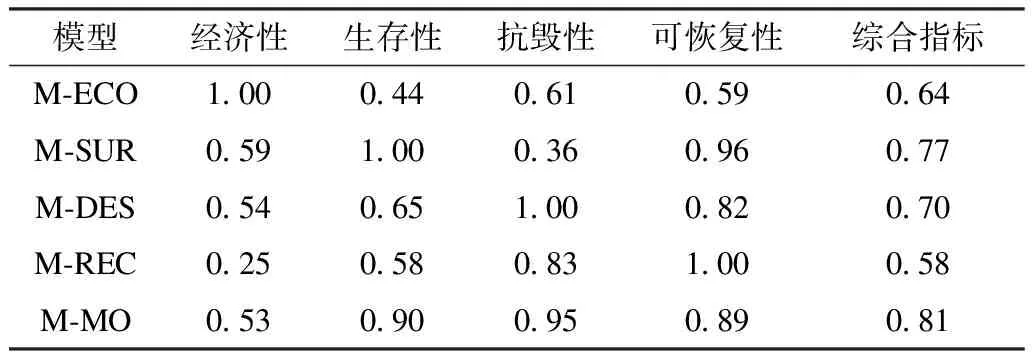
表2 M-ECO、M-SUR、M-DES、M-REC和M-MO在归一化后的经济性、生存性、抗毁性和可恢复性的对比Tab.2 Comparison of economy, survivability, invulnerability and recoverability of M-ECO, M-SUR, M-REC and M-MO after normalization

由表2可知，M-ECO追求最好的经济性，因此其生存性、抗毁性、可恢复性等抗灾性能远低于其他模型；M-SUR的生存性最高，但由于该输电网的负荷节点大多数并不位于连接多个支路的重要中枢位置，因此其抗毁性仅为0.36；同理，M-DES虽然具有最高的抗毁性，但其生存性仅为0.65；M-REC的可恢复性最高，意味着骨干网架保留的重要线路和节点越多，但同时带来的是1 958.2万元的高昂加固费用，因此其经济性仅为0.25；本文所提M-MO的生存性、抗毁性、可恢复性和经济性分别为0.90、0.95、0.89和0.53，这反映了其能够在保证优秀的抗灾性能的同时具有良好的经济性。此外，表2将5种模型的经济性、生存性、抗毁性和可恢复性通过熵权法求得的加权系数按照式(18)进行加权得到综合指标，其中M-MO的综合指标达到0.81，高于其他4个模型，进一步验证了本文所提M-MO的有效性。

为验证本文所提嵌入图论修复策略的改进NSGA-Ⅱ在收敛性能方面的有效性，将本文所提算法和嵌入图论修复策略的粒子群算法[1 - 3]在收敛性能方面进行对比，结果如图5所示。由图5可知，本文所提算法在迭代过程中，每一代的Pareto最优解的归一化多目标函数加权值总体上呈增加趋势，而粒子群算法则处于不断波动的状态，可见本文所提算法在收敛性方面优于粒子群算法。此外，在个体/粒子数均为100，迭代次数均为100的前提下，本文所提算法和粒子群算法的模型求解时间分别为3 076 s和3 646 s，验证了本文所提算法在计算性能方面也更具优势。

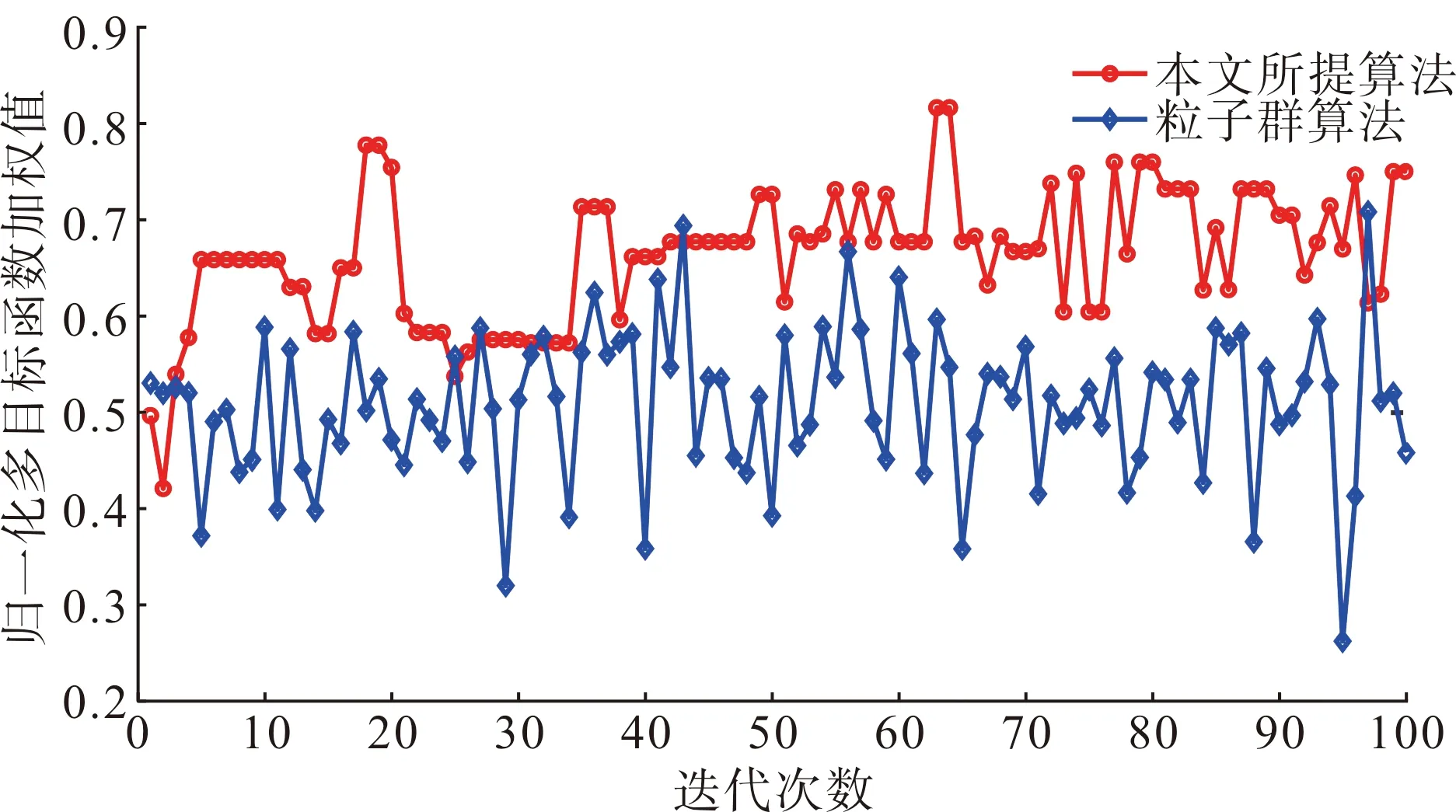
图5 本文所提算法和粒子群算法在收敛性能方面的对比Fig.5 Comparison of the proposed NSGA-Ⅱ and particle swarm optimization on convergence performance

5 结语

本文提出一种以最大化骨干网架规划经济性、生存性、抗毁性和可恢复性为多目标函数的骨干网架多目标规划方法。算例分析结果表明，本文所提模型得到的骨干网架规划策略能够兼顾骨干网架的规划经济性和多阶段抗灾性能，相比骨干网架单目标规划模型而言，能够给出在经济性、生存性、抗毁性和可恢复性等方面更加均衡和全面的骨干网架规划策略。