基于CFD的仿鲹科机器鱼动力学建模与运动控制

张宜阳，汪 明，杜晓彬，王昆仑

(山东建筑大学 信息与电气工程学院，济南 250101)

0 引言

近年来，有许多高校都在进行仿生机器鱼的研究，其中因为具有高速、高效、高机动性等优点，身体/尾鳍推进(BCF,body and/or caudal fin propulsion)模式的仿鲹科机器鱼逐渐成为仿生机器鱼的研发重点[1]。例如Wang等人使用粒子群优化(PSO，particle swarm optimization)算法和中枢模式发生器(CPG,central pattern generators)模型[2]来获取四联机械鱼的最大平均速度和最大推进效率[3]。汪明等人设计了一种基于CPG控制的机器海豚，通过实验验证了所提出的机器海豚的有效性和实用性[4]。Yu等人研发了一种无线电控制的四连杆仿生机器鱼及其控制系统，文章实现了点对点 (PTP，point to point) 控制算法，并采用了高架视觉系统来提供实时视觉反馈[5]。Yu等人构建了一种用于展览目的的新型仿生海豚，通过实验室实验和现场实验证明了基于CPG的步态生成方法，具有明确的频率和幅度可调性，而且具有很强的交互性[6]。尽管现阶段已经有很多仿鲹科机器鱼及其控制方法，但随着流体力学技术和计算机技术的发展，人们发现机器人形态特征和运动方式对于仿生机器人的设计和复杂行为研究至关重要[7-9]。由于计算流体力学仿真可以直观的显示和说明肉眼不可见的流场状态，并且大大减少了实验所用的费用，缩短了实验周期，因此有关机器人系统的流体力学建模也多了起来[10]。Yu等人建立了多关节仿生机器鱼的动态模型并且进行了实验仿真，提供了一个很好的仿鲹科机器鱼CPG耦合动力学模型[11]。Dong等人提出了一种仿生鲸鲨式水下滑翔机的创新设计，通过计算流体力学方法，验证了鲸鲨式滑翔机的滑翔能力[12]。Wu和Yu等人建立了一个全状态的滑翔机器人海豚动力学模型，说明了所开发的滑翔机器人海豚的强大运动能力，并验证了所制定的动态模型的有效性[13]。Yu等人提出了一种动力学模型，其应用于具有CPG耦合的仿生机器鱼上，为鲹科仿生机器鱼的运动模式提供了良好的思路[14]。薛文奎等人对于仿鲹科的双体耦合系统进行了动力学研究，验证了双体机器鱼反相波动耦合推进的优越性[15]。K.A.Morgansen等人考虑了机器鱼的运动控制算法设计，应用非线性控制方法对一种平面的仿鲹科推进的机器鱼进行了建模和控制设计[16]。于浩然等人利用Fluent完成了对碟形水下机器人黏性流场阻力分析[17]。Wang等人通过建立3D的动力学模型来研究仿生海豚的机动性，为水下滑翔仿生海豚的真实应用提供了有价值的指导[18]。马影等人利用计算流体力学(CFD，computational fluid dynamics)方法对蝠鲼的非定常水动力特性进行了模拟分析[19]。夏丹等人采用数值模拟方法对鲹科模式机器鱼的自主游动机理进行研究，其结果对于获得更为合理的三维机器鱼的稳态游动机理有着重要意义[20]。吴文广以鲹科模式鱼类作为研究对象进行了一系列的仿真，其结论对进一步开展鱼类推进机理研究和仿鱼类推进器的研制,提供了重要的参考依据[21]。

本文以流体力学分析为切入点，基于计算流体力学方法，利用Fluent软件对构建的鱼体模型使用采集到的金枪鱼鱼尾摆动数据和鱼体波方法进行仿真，分析仿生机器鱼在应用两种方法时，不同摆动频率和幅度对游动速度的影响，同时也通过真实的实验验证上述仿真结果的正确性，为优化仿生机器鱼的运动控制提供一种新的思路。

1 仿生机器鱼动力学建模

本文采用的仿真软件为Fluent，其能够运用计算流体力学方法得到给定流体区域内的离散解，细致描述给定流场内部的参数变化。

1.1 流体力学基本方程

所有的流体问题都遵守着质量守恒定律、动量守恒定律和热量守恒定律。本次仿真中不考虑热量交换问题，故热量守恒定律不在考虑范围之内。质量守恒定律的数学表达式如下：

(1)

式中，ux，uy，uz分别为x，y，z方向在t时刻的速度分量，t为时间，ρ为流体密度。质量守恒定律保证在单位时间内流入系统的流体净质量和该系统在单位时间内的质量增量是相等的。

动量守恒定律的数学表达式描述了在粘性不可压缩的流体系统内，系统内所受的外力的总和等于系统内部的动量的变化率。动量守恒定律的数学表达式为纳维斯托克斯方程，纳维斯托克斯方程在直角坐标系的表示如下：

(2)

式中，ρ为流体密度，ux，uy，uz分别为x，y，z方向在t时刻的速度分量，τ为应力张量，F为应用在物体上的力，若物体只受重力影响时，Fx=Fy=0，Fz=ρg。

1.2 有限体积法

可以看出描述流体问题的方程都为偏微分方程，为了解决偏微分方程很难求出其解析解的问题，目前主流的CFD软件大部分都采用有限体积法(FVM, finite volume method)。有限体积法又称有限容积法、控制体积法，其基本思路是将给定的计算域划分成互为独立且不相同的子区域，并且在这些子区域内，通过网格的划分设定节点，建立离散方程。通过上述操作后，计算域的偏微分方程就变成了每个节点上的代数方程组，便可以对其进行求解。

1.3 建模及仿真

本文使用Fluent仿真软件进行仿真计算有三个步骤：前处理、计算求解和后处理。前处理包括鱼体几何模型的建立、计算域的划分、网格的划分、边界条件的设定和控制参数的设定，其目的为创造计算求解步骤所需的模型，为下一步进行仿真实验奠定基础。计算求解则是利用CFD求解器，在已经建立好的模型行进行求解运算，输出数据。后处理则是通过后处理软件对求解的量进行处理分析。建模仿真流程如图1所示。

图1 建模仿真流程图

1.3.1 仿真模型的构建及实验

本仿真所用的鱼体模型使用SoildWorks软件构建，构建的仿生机器鱼3D模型仿照鲹科鱼外形，其尺寸如图2所示。

图2 仿生机器鱼3D模型

本仿真构建的鱼体模型在游动时采用鱼体波产生的数据和金枪鱼游动时采集数据两种运动控制方式。鱼类在游动时，鱼头至鱼尾呈现出的一个身体波动规律。Lighthill[22]提出的鲹科鱼类鱼体波模型：

(3)

式中，Ybody(x,t)为鱼类沿垂直中心线摆动的幅值，x为鱼类沿鱼尾至鱼头方向上的位移，c1、c2分别为鱼体包络线的一次系数、二次系数，λ为鱼体波波长，在本次仿真实验中，所用c1、c2和λ的取值分别为0.08、0.000 1和1.7。

在以大数据作为背景的媒体发展主要呈现出一种新媒体与传统媒体相融合的现象，媒体的融合发展成为了媒体行业的重要任务。根据我国当下的媒体融合现状，媒体融合这一重要工作仍存在较多问题，尤其是对新媒体与传统媒体融合的意义以及重要性的领悟上存在缺陷。首先，有极大一部分媒体工作者对于媒体融合的目标不清晰，阻碍了媒体融合的高速发展；其次，媒体工作者对大数据时代的认识较为欠缺，对大数据技术的掌握不到位，媒体工作者的综合能力水平需要提高；最后，对媒体融合的管理体系、管理制度等不够完善，需要进一步加强和改进，对传统的管理模式做出适当、有效的调整。

真实金枪鱼游动采样数据是通过计算机视觉技术，在金枪鱼的游动视频中批量地、逐帧地采集鱼的尾部位置变化，然后得到连续独立的离散数据点，模型通过读取这些数据点实现鱼的尾部的位置变化，从而实现尾部的摆动，进而实现游动。将金枪鱼游动采集的鱼尾位置离散数据经过拟合后，得到如下式的数据曲线：

Y=sin(7.346t+6.147)

(4)

式中，Y为鱼尾沿垂直中心线方向摆动的幅值，t为时间序列。图3为鱼体波数据和金枪鱼数据的在鱼尾部同一位置上的数据曲线。

图3 驱动方式数据曲线

为了对比仿真实验中不同的驱动方式，在不同摆动的频率和幅度下对游动速度的影响关系，在本次仿真中设置两组仿真，其中的一组仿真使用金枪鱼游动采样数据，另一组使用鱼体波数据，仅改变两组仿真中鱼尾摆动的频率和幅度进行仿真实验，以减少其他变量对本仿真的干扰。每一组内设置了鱼尾摆动频率为1 Hz、2 Hz，鱼尾幅值为4 cm、8 cm，共四组对比仿真。设置的仿真实验如表1所示。

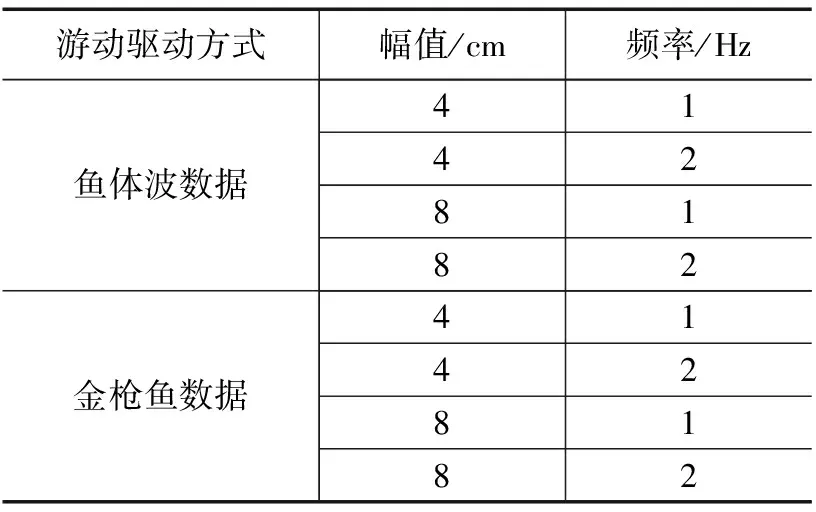
表1 仿真实验组

1.3.2 网格划分及边界条件设定

本仿真使用动网格重叠方法实现仿真中鱼体的游动。首先划分出计算网格和背景网格。鱼体的网格区域采用四面体为主的非结构网格，背景网格采用四面体结构网格，这样划分网格的优点是，鱼体的网格区域采用四面体为主的非结构网格能够满足CFD求解器对瞬态计算的网格精度要求。而背景网格由于受鱼体游动影响不大，故设定四面体结构网格，以减少计算量。在建立模型时设置计算网格和重叠网格(Overset)，实现动网格的重叠。边界条件的设置如图4所示。

图4 仿真模型边界条件

图4(a)中上、下、左、右4个面为固定壁面，图4(b)中左面设置为速度入口，来流速度为1 m/s，右壁面设置为压力出口，设置背景区域的流体介质为水。使用用户自定义文件(UDF)宏定义实现鱼体的游动方式、游动方向和速度的计算。粘性模型采用k-ω模型，选择Low-Re矫正，采用瞬态计算，并行计算。仿真模型中，流体介质为水，密度为998.2 kg/m3，粘度为0.001 kg/m-s，来流速度为1 m/s，特征长度为0.04 m，因此模型的雷诺数Re为4×103。划分网格后的流体域模型如图5所示，其中节点为118 311个，单元为245 220个。

图5 划分网格后的流体域

设置好仿真环境后，进行的仿真鱼体模型游动如图6所示。

图6 游动示意图

2 仿真结果分析

在应用两种不同的游动驱动方式，且只改变鱼体摆动频率和幅度的情况下，按照上述所建立的仿真模型，进行计算后，每个仿真所得出的鱼体速度在t=1 s、t=3 s、t=5 s时如表2所示。

表2 不同时刻的速度 m/s

从表2中可以看出，无论是改变频率还是改变幅度，都会对速度产生影响，且改变幅度对改变频率对速度的影响更大。若是将频率和幅度都同时增大，速度变化最为明显。

为了更直观地分析两种游动方式对速度的影响，图7表示了在相同的摆动频率和摆动幅度下，不同的游动方式对速度的影响。

图7 不同游动方式速度变化对比

可以看到，在图7(a)中，使用鱼体波数据和使用金枪鱼数据的速度变化并没有明显的差别，这说明在低频率、小幅度的游动中，两者的差距不大；在图7(b)中，使用金枪鱼数据的速度要略快于使用鱼体波数据的方法；但是在图7(c)中，使用金枪鱼数据的速度比使用鱼体波数据的速度快8.1%；在图7(d)中，使用金枪鱼数据的速度也要明显略快于使用鱼体波数据的方法。

图8为上述各仿真在5 s时的速度对比图。

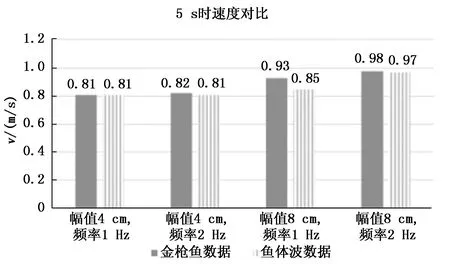
图8 两种驱动方式在第5 s时速度对比

从图中可以看出，仿生机器鱼在小幅值游动时，两种驱动方式速度相差无几，但是在大幅值游动时，使用金枪鱼数据驱动方式的速度要明显大于鱼体波数据的方式。

在低频率、大幅度的情况下，通过仿真得到了鱼体使用两种驱动方法所产生的推力，如图9所示。

图9 两种驱动方式产生的推力

从图9可以看出，使用金枪鱼数据方式所得到的推力数值要大于使用鱼体波数据方式。两种推进方式所得到的推力波形相似，都是在0.2 s左右到达峰值，然后下降到最低值，之后按照正弦规律变换。可以看到，从0.5 s开始，使用金枪鱼数据驱动方式的推力波形的峰值达到了1.4 N，与最低值得差值为0.6 N；使用鱼体波数据方式的推力波形达到了1.3 N，与最低值相差0.8 N。根据上述可以得出结论，使用鱼体波数据方式和金枪鱼数据方式的推力波形相似，但在数值上，不管是波形的最大值还是最小值，使用金枪鱼数据方式的推力要整体大于使用鱼体波数据方式的推力，且使用金枪鱼数据方式的推力波形的插差值要小于使用鱼体波数据方式。由此可知，在低频率、大幅度的情况下，使用金枪鱼数据方式所产生的推力，大于使用鱼体波数据方式产生的推力，因此使用金枪鱼数据的方法速度更快。

综上所述，在小幅度的游动模式中，两种驱动模式的速度没有明显的差别；在大幅度，尤其是低频率大幅度的游动模式中，使用金枪鱼数据方法的游动效果是明显优于使用鱼体波数据方式的。因此，金枪鱼数据方法相较于鱼体波数据方法，更适合仿生机器鱼在大幅度摆动的情况下游动。

3 实验结果与分析

为了验证上述的仿真结果的正确性，本文在搭建的实验平台上应用两种控制方法进行实验。实验所用的实验平台如图10所示。

图10 实验平台

图10中，上位机控制仿生机器鱼进行应用两种控制方法的实验，摄像机记录实验结果，水池提供实验环境。

本文的实验分为4个部分，分别为使用鱼体波数据方式小幅值、金枪鱼数据方式小幅值、鱼体波数据方式大幅值、金枪鱼数据方式大幅值，每个部分中设置鱼尾部摆动幅度大幅值为25 cm、鱼尾部摆动幅度小幅值为15 cm，鱼尾部摆动频率分别为1 Hz、1.5 Hz、2 Hz的对比实验。这样设置实验组的目的是，能够通过实验得出不同驱动方式在不同的幅度和频率下的仿生鱼的游动速度，从而反映出驱动效果。

图11显示的是使用鱼体波数据方式，在小幅值摆动的情况下的位置与时间变化图。

图11 鱼体波数据驱动方式小幅值摆动

从图11中可以发现，仿生机器鱼都是从水池的左侧开始，以到达水池的右侧为结束，图中的时间分别表示仿生机器鱼在开始游动时、仿生机器鱼到达中间位置时、仿生机器鱼到达结束位置时的时刻。以此，便可以使用时间表示仿生机器鱼的游动速度，游动速度越快，则方法的效果越好。通过对比可知，在使用鱼体波数据驱动方式小幅值摆动的情况下，频率越快，游动速度越快。且仿生机器鱼到达中间位置所用的时间基本为整体所用时间的一半，表明仿生机器鱼在匀速运动。

对比以上3个不同频率的实验可知，在使用鱼体波数据驱动方式进行小幅值摆动时，仿生机器鱼会进行匀速的直线运动，且提升摆动频率对于游动速度的提升效果是明显的，摆动频率越快，则游动速度越快。

图12显示的为使用金枪鱼数据方式，在小幅值摆动的情况下进行的3组实验。

图12 金枪鱼数据驱动方式小幅值摆动

图12中可以看出，增大频率对于提升游动速度的效果是明显的。在频率为1 Hz、1.5 Hz时，仿生机器鱼游动至中间位置的时间为游动时间的一半，但频率为2 Hz时，到达中间位置所用的时间超出了整体游动时间的一半，游动过程的后半段所用时间占全部游动时间的1/3，这表明在游动过程中仿生机器鱼的加速时间大于匀速游动的时间。由此可得出结论，在使用金枪鱼数据驱动方式进行小幅值摆动时，提高摆动频率能够提升仿生机器鱼的游动速度，但是在低频时提升频率的效果不大，在频率翻倍时，仿生机器鱼的游动速度提升明显。

图13显示的为使用鱼体波数据方式，在大幅值摆动的情况下进行的实验。

图13 鱼体波数据驱动方式大幅值摆动

从图13中可以看出，摆动幅度的越大，仿生机器鱼的游动速度也越快，且仿生机器鱼到达中间位置所用的时间大约都为整体游动时间的一半，仿生机器鱼进行匀速直线运动。由此可知在使用鱼体波数据方式进行大幅度的游动时，提高摆动频率能够增快仿生机器鱼的游动速度，且改变低频时，速度变化明显，从中频到高频，速度提升较小。

图14显示的为使用金枪鱼数据方式，在大幅值摆动的情况下进行的三组实验。

图14 金枪鱼数据驱动方式大幅值摆动

图14中可以看出，仿生鱼进行匀速直线运动，且摆动频率越快，游动速度越快。改变频率对于仿生机器鱼的速度变化影响明显。

整理以上4组实验的所有平均游动速度，得到了速度对比图，如图15所示，其中摆动的大小幅值指仿生机器鱼尾鳍部位摆动的幅值。

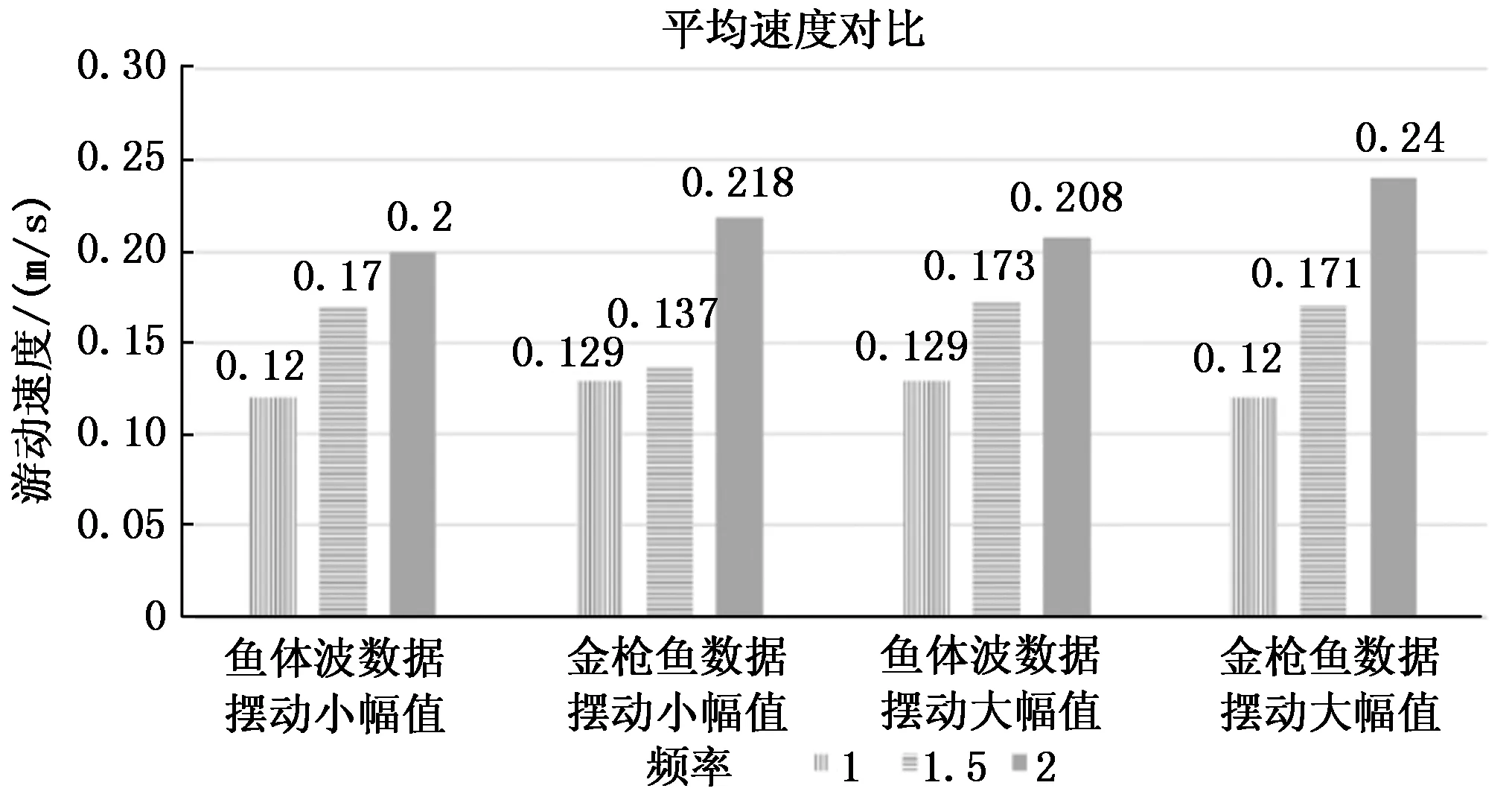
图15 实验平均速度图

分析图中的游动速度可以看出，无论应用何种驱动方式和摆动幅度，频率的快慢和平均游动速度成正相关，频率越快，平均游动速度越大。在频率一定的情况下，增大幅度也能够增加平均游动速度，无论应用何种驱动方式和摆动频率，摆动幅度增大，平均游动速度也会增大，且使用金枪鱼数据方式的平均游动速度的增幅要大于使用鱼体波数据方式。

在摆动频率为1 Hz时，使用金枪鱼数据大幅值的游动和使用鱼体波数据大幅值游动的速度相等，且大于剩下两组的平均游动速度。但无论摆动幅度和驱动方式如何变化，平均游动速度均为每组实验中的最小值。在摆动频率为1.5 Hz时，使用金枪鱼数据驱动方式，使用鱼体波数据方式和使用金枪鱼大幅值摆动数据的平均游动速度相差无几，但小幅度摆动时的效果并不理想，要远远低于其他三组实验的平均游动速度。在摆动频率为2 Hz时，使用金枪鱼游动采样数据摆动方式无论摆动幅度的大小，游动效果都要强于使用鱼体波数据游动方式，且仿生机器鱼以大幅值摆动时，对鱼体波数据方式的游动速度要比小幅值摆动的提升程度大。

总结上述的实验结果可以看出，仿生机器鱼在以中低频率摆动时，无论使用何种驱动方式和摆动幅度，仿生机器鱼的游动效果没有明显的区别，但以高频率摆动时，使用金枪鱼数据驱动的效果要明显强于使用鱼体波数据方式，在小幅度摆动的情况下，使用金枪鱼数据的游动速度要比使用鱼体波数据方式的游动速度高出9%；在大幅度的摆动情况下，使用金枪鱼数据的游动速度要比使用鱼体波数据的游动速度高出15.4%。因此得出结论，金枪鱼数据驱动方式比鱼体波数据更适合高频率、大幅值的游动情况。

4 结束语

本文对使用不同的两种游动方法进行了模拟仿真，比较了在两种游动方法下不同摆动频率和不同摆动幅度对鱼体速度的影响。通过仿真可以看出，使用金枪鱼游动采样数据方法相较于使用鱼体波数据方法更适合在鱼尾摆动频率一定、摆动幅度大的情况下使用。又通过实验验证了仿真结果的正确性。这为仿鲹科机器鱼的运动控制提供了一种新的、高效的思路，使仿鲹科机器鱼的运动控制不在局限于鱼体波方程，为仿鲹科机器鱼能够更快速、更高效的控制方法提供了指导。在今后的研究中，将继续对使用金枪鱼数据驱动方法的适用性及其转弯性能进行研究。