全向重载AGV多轴协同运动控制研究

张德政，汪步云,2，杨 鸥，陈 龙

(1.安徽工程大学 机械工程学院,安徽 芜湖 241000；2.芜湖安普机器人产业技术研究院,安徽 芜湖 241007；3.衡阳合力工业车辆有限公司,湖南 衡阳 421000)

0 引言

重型材料的自动搬运一直是物流行业的技术难点，特别是在生产车间、仓库等空间有限的工作条件下，迫切需要解决重载AGV(automated guided vehicle)灵活的运动并且在转向时实现高效的协同[1]。

在发达国家中，美国、日本、德国、瑞典等多国家都发布支撑移动机器人发展的战略文件，其移动机器人种类齐全，技术水平处于领先地位[1]。中国的移动机器人技术起步较晚,但是关于移动机器人的研究正在迅速发展,在近几年取得了较大的突破。基于麦克纳姆轮结构设计，G.Bayar等设计了新型的悬架机构，减小了麦克纳姆轮产生的高频振动，运用多传感器数据融合的方法，实现了灵活的转向。谢永良等[3-4]推导出了AGV基于Ackermann转向的数学模型，运用PID控制算法，在转向时，从动轮能快速响应，实现了高精度转向。

目前，在重载、高精度、存在较大负载扰动的系统中，多电机协同控制是最核心的问题[5]。同步控制算法直接影响着系统的稳定性、准确性及工作效率，故一部分学者对其进行了更为深入的研究。Q.Sun[6]等采用了改进的偏差耦合控制，并验证了在四电机转速相同时具有较高的同步性。谷雨等[7]提出加权交叉耦合控制算法，同时验证了算法的稳定性，仿真结果表明对多个功率不同的电机具有较好的同步性。张承慧等[5]运用最小相关轴数目的同步思想，结合环形耦合控制，结果表明在受到干扰时误差收敛速度快。王慧霞等将迭代学习和交叉耦合结构相结合的控制策略运用于伺服数控系统中，提高了零件的加工精度。王丽梅等[9]将经验模态分解算法与交叉耦合控制策略相结合以提高控制的精度。

全向AGV在结构上多采用麦克纳姆轮式的和双舵轮式，麦克纳姆轮承载能力相对较弱，适用的环境有限[10]；双舵轮式重载AGV灵活程度不高[11]。在多电机控制策略上，交叉耦合控制策略对双电机系统具有较高的协同性和抗干扰能力[12-13]。故本文基于四舵轮式全向重载AGV机械结构，在转向工况下，采用BAS算法对单轴控制系统进行PID参数整定[14-21]，运用交叉耦合控制策略，设计多电机协同的运动控制算法，可以抵抗负载扰动能力强，灵活程度高，实现了全向重载AGV在狭小的空间内灵活的转向。

1 硬件控制系统构建

1.1 全向重载AGV的底盘机械结构

底盘三维结构如图1所示。全向重载AGV的底盘机械结构主要由车身、舵轮安装板及舵轮3部分组成。车身由中间两道工字钢、两侧的槽钢及横向放置的钢板组成，通过横向放置的钢板将工字钢和槽钢焊接为一体，舵轮安装板焊接于工字钢上，舵轮由螺栓连接安装于舵轮安装板上。全向重载AGV的主要设计参数如表1所示。

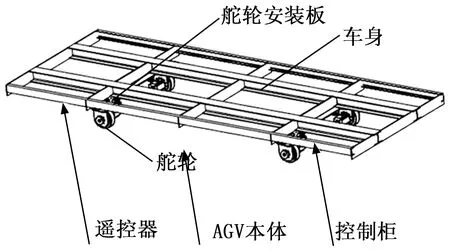
图1 全向重载AGV的车身结构

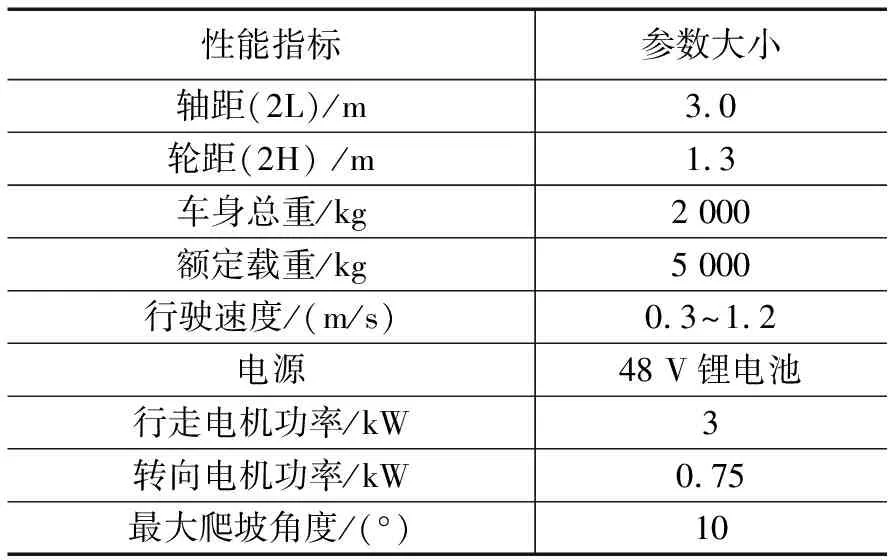
表1 全向重载AGV设计主要参数

1.2 控制系统硬件设计

本文基于四舵轮式重载AGV,根据AGV欲完成的动作、输入输出接口需求及通讯协议等，设计了全向重载AGV控制系统的硬件部分，使8个电机能流畅的完成预定转向动作。

如图2所示，控制系统主要由3部分组成，包括信号输入、控制信号分析以及控制信号执行。在左前轮和右前轮中心处安装有磁导航传感器，磁导航传感器通过RS485总线将AGV实际位置与预定位置的偏差量输入到CM-1241模块,再送至CPU1214C。控制信号分析主要负责信息的汇聚、分析及分类发送等任务，由CPU1214C模块和CM-CANOPEN模块组成。CPU1214C对输入的信号分析处理，再由CM-CANOPEN模块将信号以CANOPEN协议输送到伺服电机驱动器。控制信号执行为转向电机接收到指令后完成相应的动作，再由编码器反馈动作实际完成的情况。

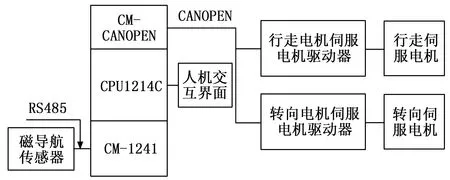
图2 全向重载AGV控制系统

1.3 全向重载AGV转向数学模型

在前后轮同角度转向的这种典型工况下(假设绕着瞬心逆时针转向)，如图3所示，图3中主要参数说明如表2所示，4个轮子的转角应满足：

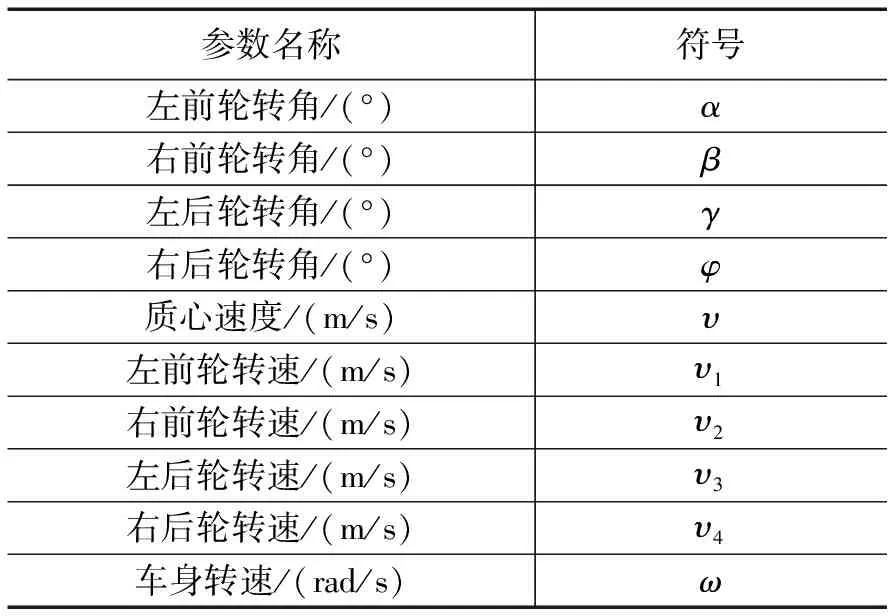
表2 AGV转向主要参数说明

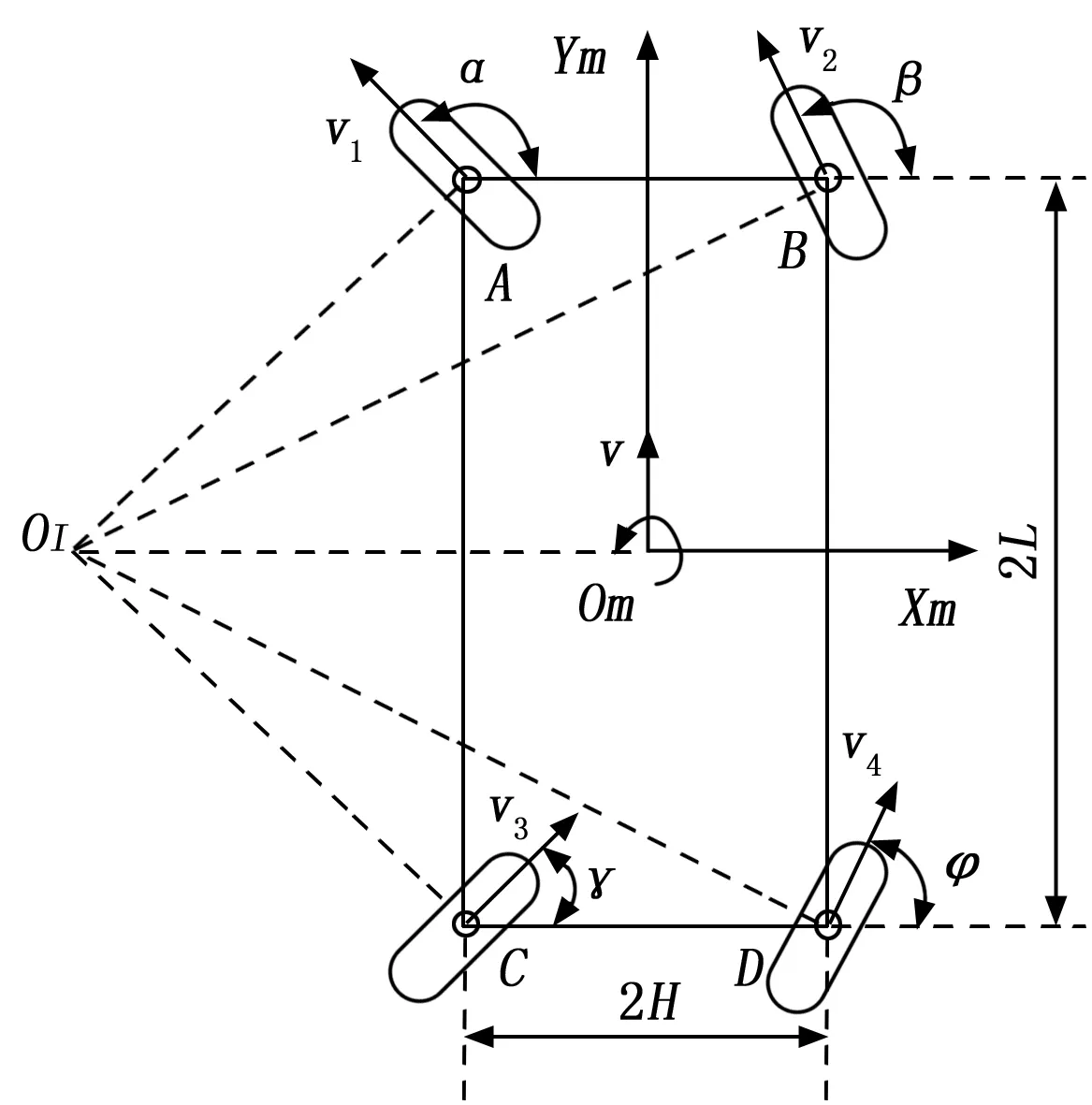
图3 前后轮同角度转向示意图

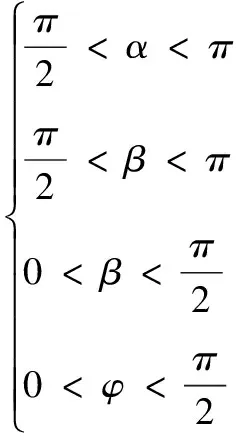
(1)

式中，α为左前轮转角，β为右前轮转角，γ为左后轮转角，φ为右后轮转角。

则在此转向方式下四轮的转角关系为：

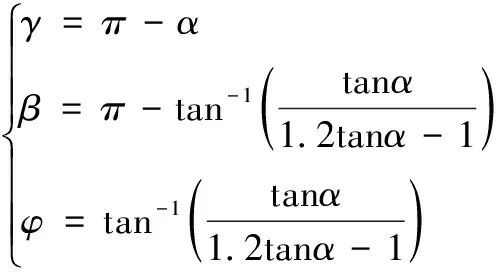
(2)

2 单轴控制算法设计

2.1 转向电机数学模型

建立永磁交流伺服电机的数学模型，将其理想化为线性状态[3]方程为：

(3)

转向电机采用功率为750 W的Motec永磁交流伺服电机，为提高转向电机的控制精度及抗干扰能力，加入电流环、速度环及位置环，闭环系统数学模型如图4所示，电机的主要参数如表3所示。虚线框为转向电机的开环传递框图，将表3参数代入，可得传递函数为：

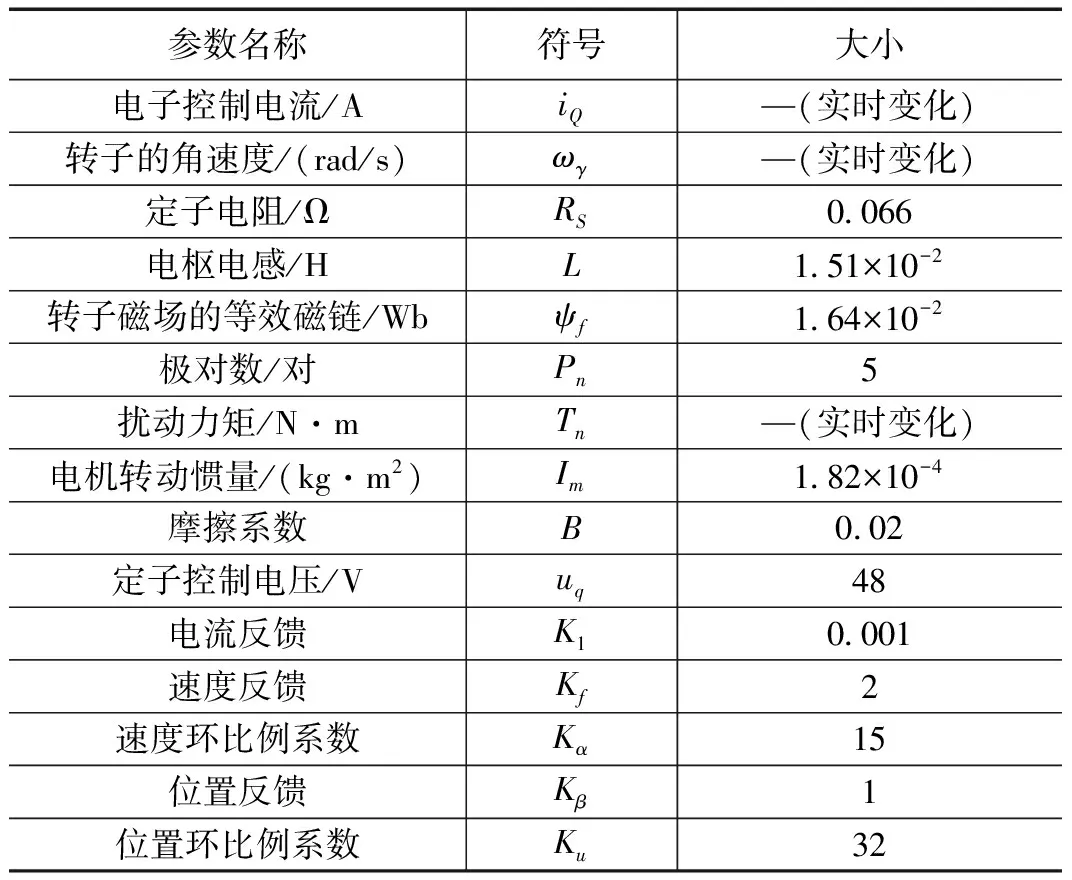
表3 电机的主要参数

图4 转向电机闭环系统数学模型框图

(4)

2.2 基本天牛须搜索算法

天牛须搜索(BAS,beetle antennae search algorithm)算法是一种生物启发式优化算法。其基本仿生学原理为天牛两根触角感知到的食物气味浓淡来觉得自己下一时刻的前进方向[15]。参照该行为方式抽象出BAS算法的计算流程：

1) 假设一只天牛由质心和左右两须组成，如图5所示。天牛在k维优化问题的解空间中运动，初始化质心位置x，左须xleft，右须xright，两须之间的距离d。

2)生成左须指向右须的向量为:

(5)

式中,rand()为随机矩阵。

3) 计算天牛右须和左须的位置:

(6)

4) 更新天牛位置：

(7)

式中，sign为符号函数，δt为步长，f(x)为x的适应度函数。

2.3 适应度函数设计

目标函数设置为:

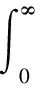
(8)

其中:e(t)为电机的跟踪误差，u(t)为PID控制律的输出,w1、w2为权值，取值范围为[0，1]。

为防止系统出现超调，在目标函数中额外引入超调项，即当e(t)<0时，此时的设置为:

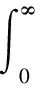
(9)

式中,w3为权值，且w3>>w1，选取w1=0.999，w2=0.001，w3=100。

2.4 BAS-PID融合算法

将BAS与常规PID算法相融合，能有效解决常规PID控制器容易出现超调且难以将参数调至最优等问题[17]。

将BAS算法与PID控制器融合过程如图6所示，参数选取如表4所示，主要融合步骤为:

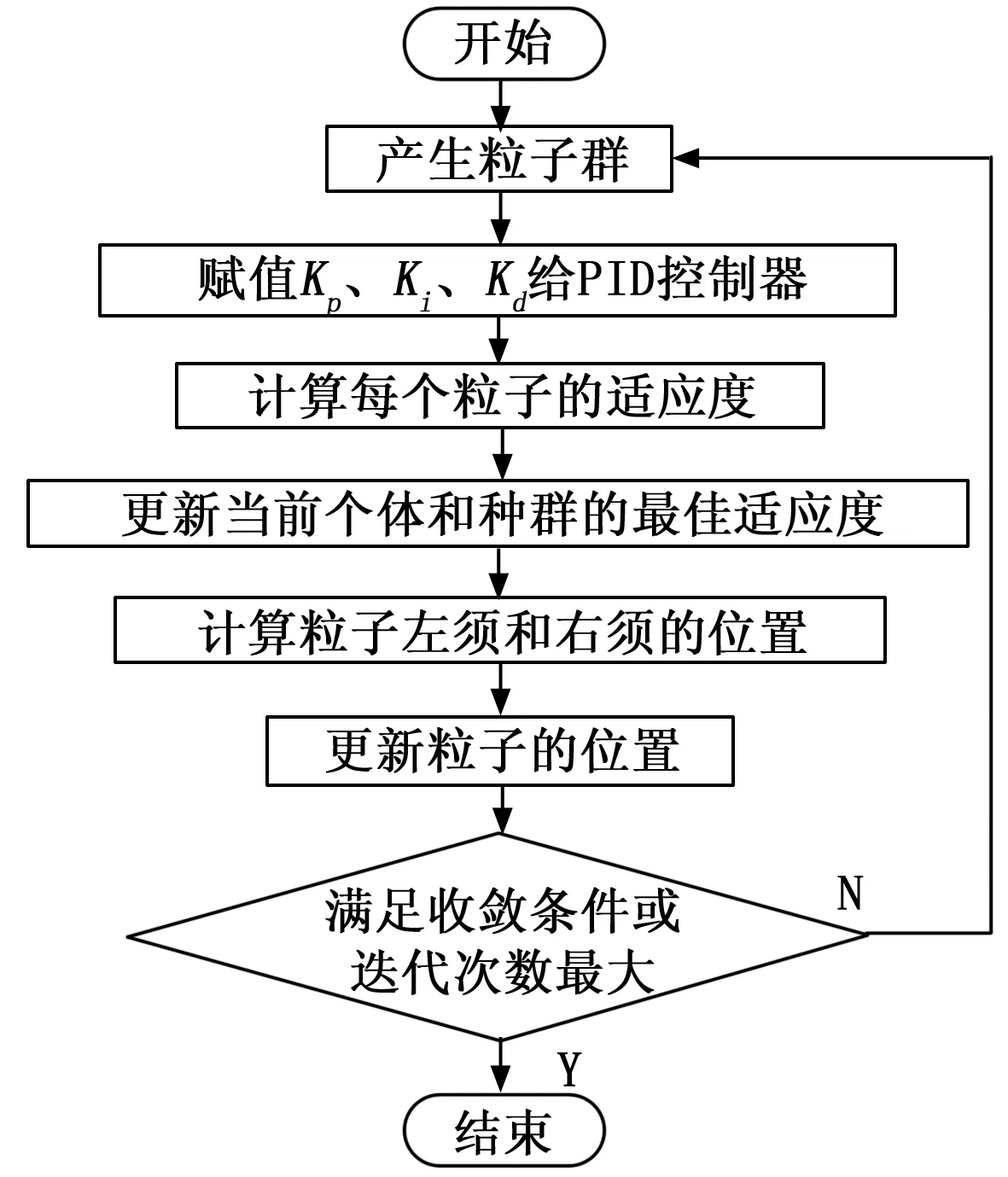
图6 BAS-PID融合算法流程图

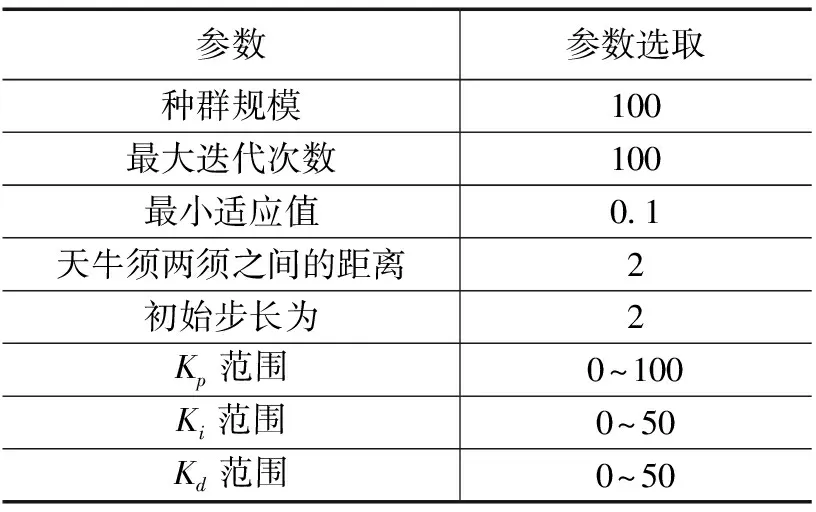
表4 BAS-PID算法参数选取

Step 0：产生粒子群并初始化粒子群，确定粒子的数量、最大迭代次数、天牛须两须之间的距离及初始步长等。

Step 1：由BAS算法随机产生的Kp、Ki、Kd的值赋给PID控制器并计算适应度值。

Step 2：将每个粒子现在的适应度值与其历史最佳适应度值对比，若现在的适应度值优于历史，则将现在的适应度值记录为最优状态。

Step 3：将每个粒子的最佳适应度值与种群历史最优适应度值比较，若粒子的最佳适应度值优于种群历史最优适应度值，则将该粒子的最佳适应度值记录群体最佳适应度值。

Step 4：对粒子位置进行更新。

Step 5：满足输出条件则输出，若不满足则继续搜索。

3 转向电机交叉耦合控制器设计

对于4台转向电机的转向运动控制系统中，设第i个电机的位置跟踪误差为：

ei(t) =θid(t)-θi(t)(i= 1,2,3,4)

(10)

式中，ei(t)表示第i台电机位置跟踪误差，θid(t)表示第i台电机由转向数学模型得到的期望转角，θi(t)表示第i台电机实际转角。其中θid(t)与AGV各轮转角之间的关系为(转向电机连接50∶1减速器)。

(11)

可以得到4个转向电机期望转角的关系为:

(12)

可以得到4个转向电机的同步误差为：

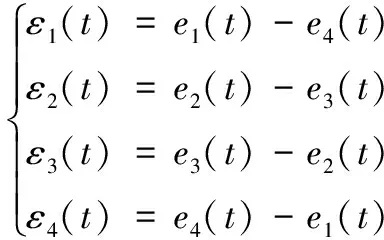
(13)

如图7、图8所示，为实现4个转向电机的协同控制，分别将跟踪误差及同步耦合误差输入到位置补偿器中，对4个转向电机进行耦合误差控制。其控制过程如下：

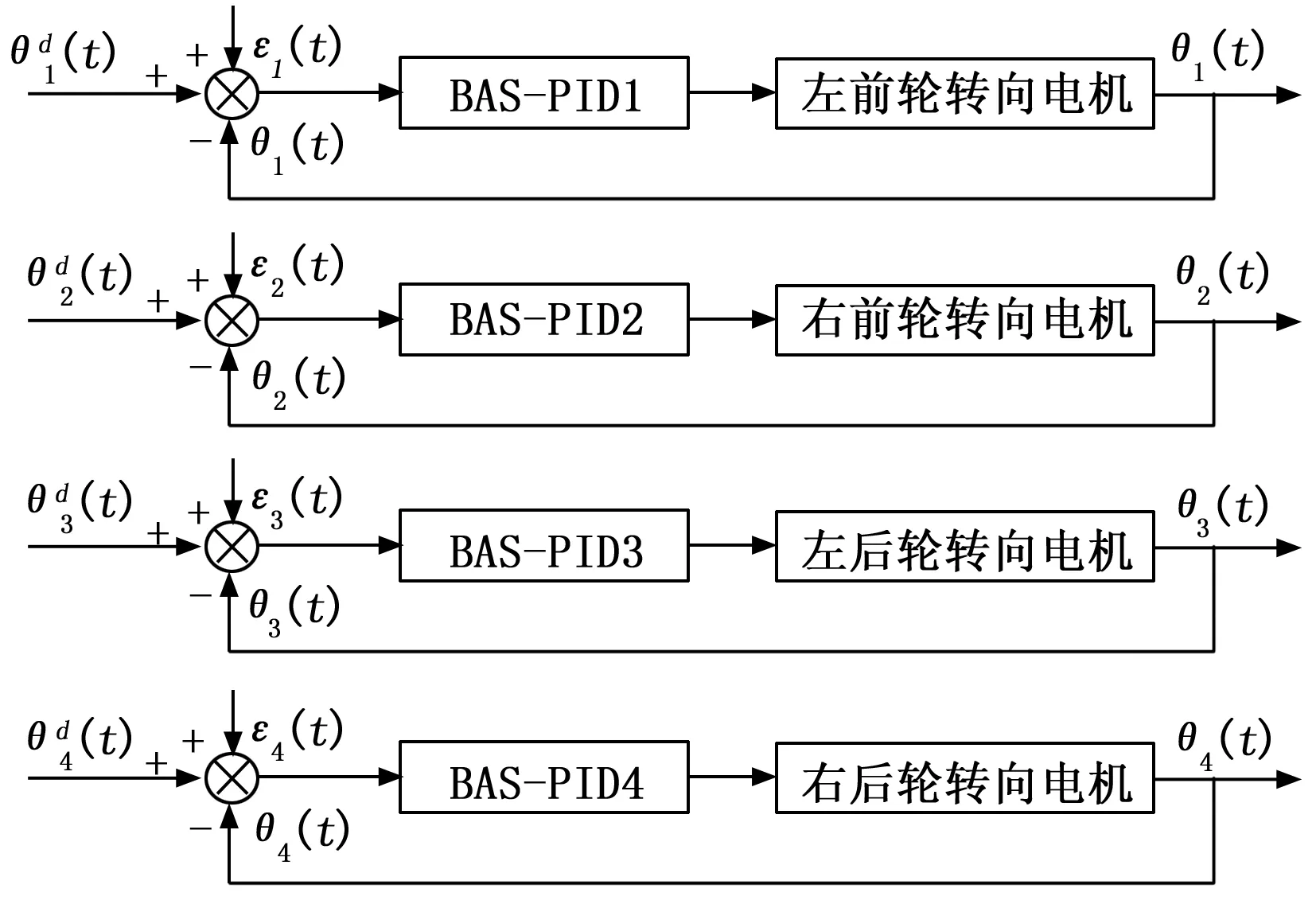
图7 转向电机控制原理框图

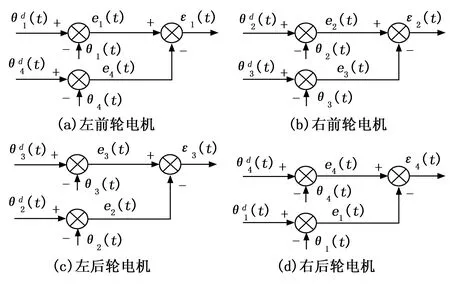
图8 四电机同步耦合误差关系图

1)将CPU1214C求得的各个转向电机的预期转角θid(t)分别与各个转向电机的编码器实时反馈实际的转角θi(t)作差，从而得到各个电机的位置跟踪误差ei(t)。如图7所示，将各个转向电机的位置跟踪误差ei(t)输入到各转向电机的BAS-PID控制器中。

2)如图8所示，将每个转向电机的位置跟踪误差分别与对角(左前轮和右后轮为一个对角，右前轮和左后轮为一个对角，)转向电机的位置跟踪误差作差得到同步误差εi(t)。

3)如图7所示，同步误差εi(t)输入到各转向电机的位置补偿器中。

4 实验

4.1 BAS_PID融合算法优化效果验证

本文分别选取天牛须搜索算法(BAS)、人群搜索算法(SOA)及粒子群算法(PSO)进行性能比较，将3种智能算法相同的初始化参数均设为一致。

在Matlab/Simulink软件中，以左前轮电机为研究对象，用3种算法对PID参数进行寻优，Simulink仿真如图9所示。由于3种算法都产生了随机矩阵，故每次结果有所不同。分别对3种算法各试验5次，以加入单位阶跃信号上升时间最短为评价标准，选取最优结果，结果如图10和表5所示，t为时间，结果表明BAS-PID寻优结果在上升时间和调整时间上优于其他两种算法，BAS-PID寻优结果的上升时间为SOA-PID寻优结果的79.7%，为PSO-PID寻优结果的81.0%。

图9 Matlab与Simulink联合仿真

图10 3种寻优算法单位阶跃信号的响应

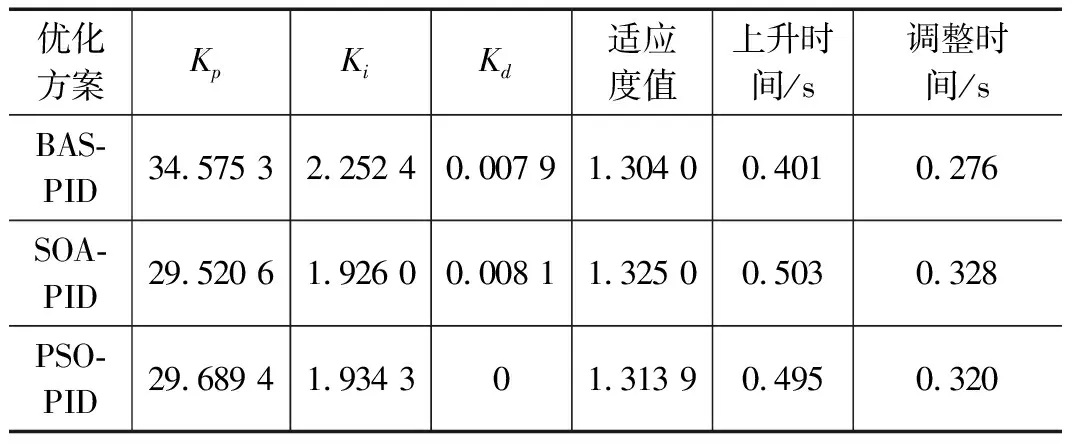
表5 3种寻优算法的性能指标

在Matlab软件中画出BAS-PID优化系统的Bode图，如图11所示。由图11可知，幅值裕度(Gm)为10.5 dB,幅值裕度(Pm)为54°，幅值裕度和相角裕度均大于0，故系统稳定。

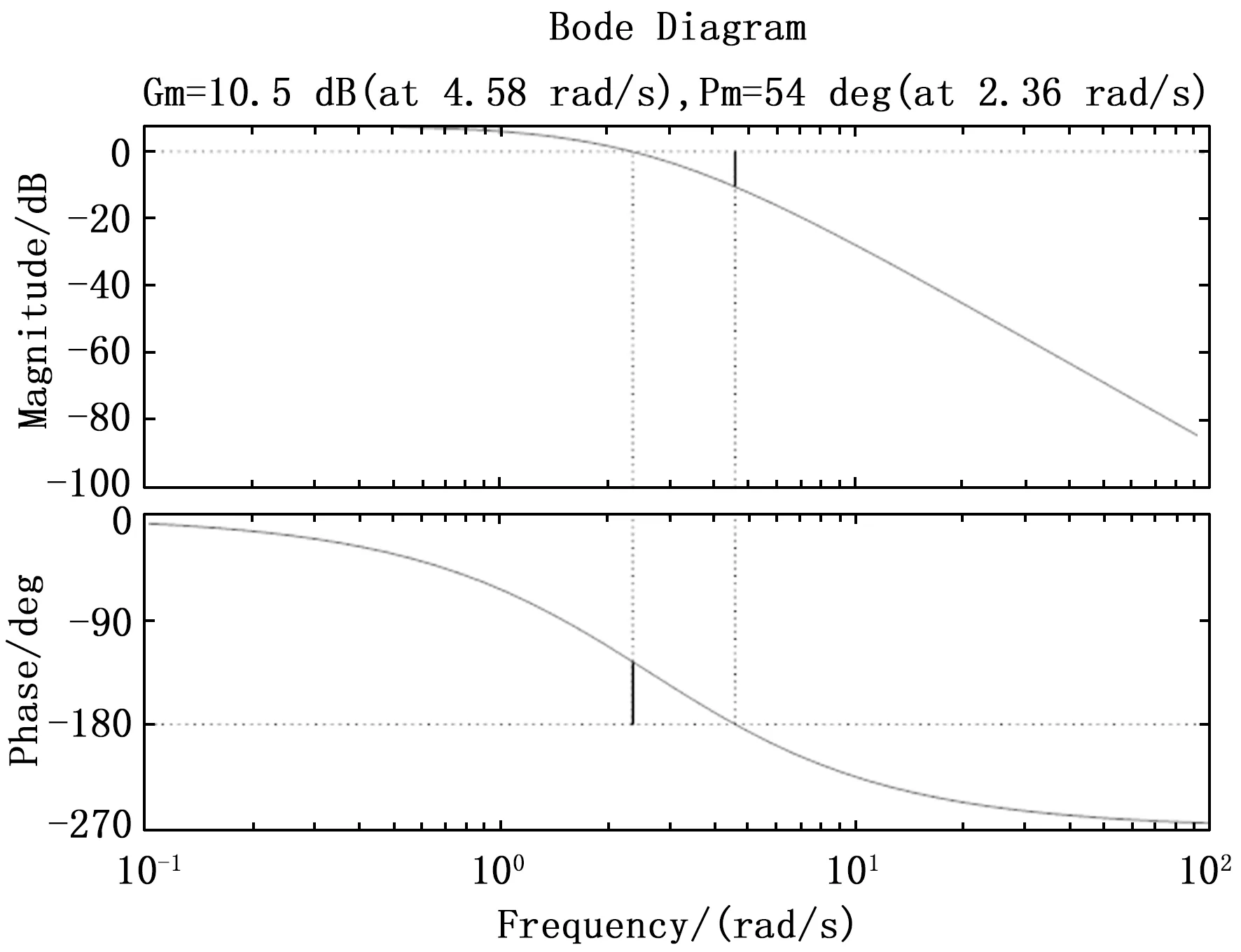
图11 BAS-PID优化系统的Bode图

以左前轮转向电机为研究对象，设置目标转角随时间的函数为,仿真时间为2 s。将表5的3组PID参数分别代入Simulink中仿真，结果如图12所示，t为时间,转角跟踪误差如表6所示。由图12和表6可以得出：

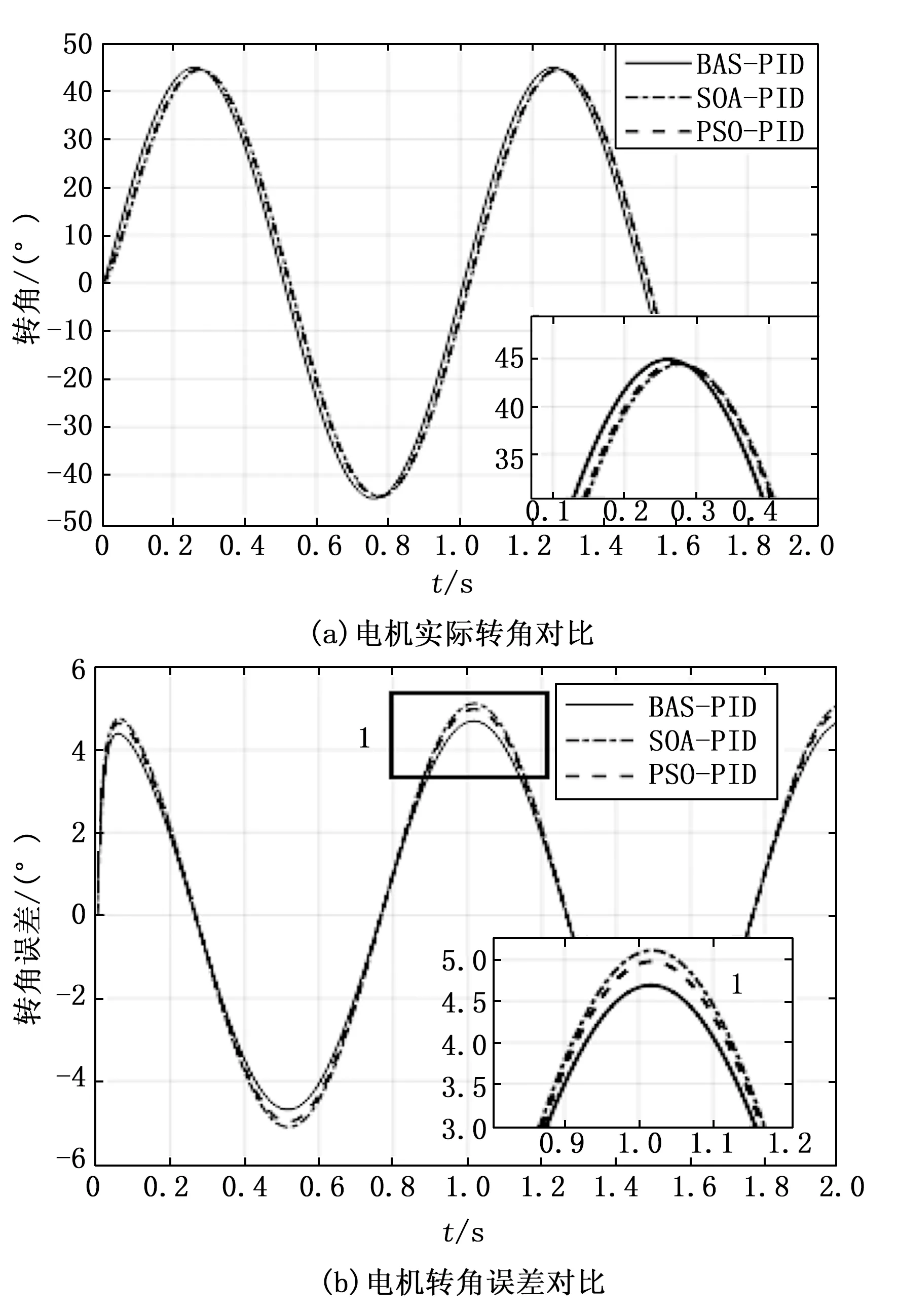
图12 3种寻优算法效果对比图

表6 3种优化方案正弦信号下跟踪误差范围度

1)运用BAS-PID优化的系统在正弦信号下的响应比SOA-PID、PSO-PID优化的系统更快。

2)BAS-PID优化的系统在正弦信号下的跟踪误差范围SOA-PID、PSO-PID优化的系统小。

4.2 多轴协同效果验证

现对前文述控制策略进行Simulink仿真验证，仿真时间为5 s。以左前轮转向电机为研究对象，设定电机转角为10度，均在2 s时设置外界加入4 N·m负载干扰，对比有交叉耦合控制和无交叉耦合控制时左前轮电机实际运行的转角(有交叉耦合和无交叉耦合仿真模型中PID参数均设为Kp=34.573 5，Ki=2.252 4，Kd=0.007 9)。

结果如图13所示，图中t表示时间，瞬态响应比较如表7所示。结合图13和表7可以得出：

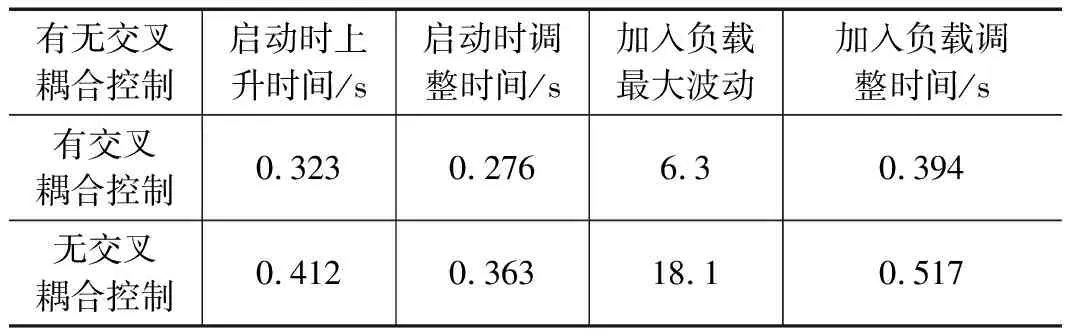
表7 有无交叉耦合控制的瞬态响应比较

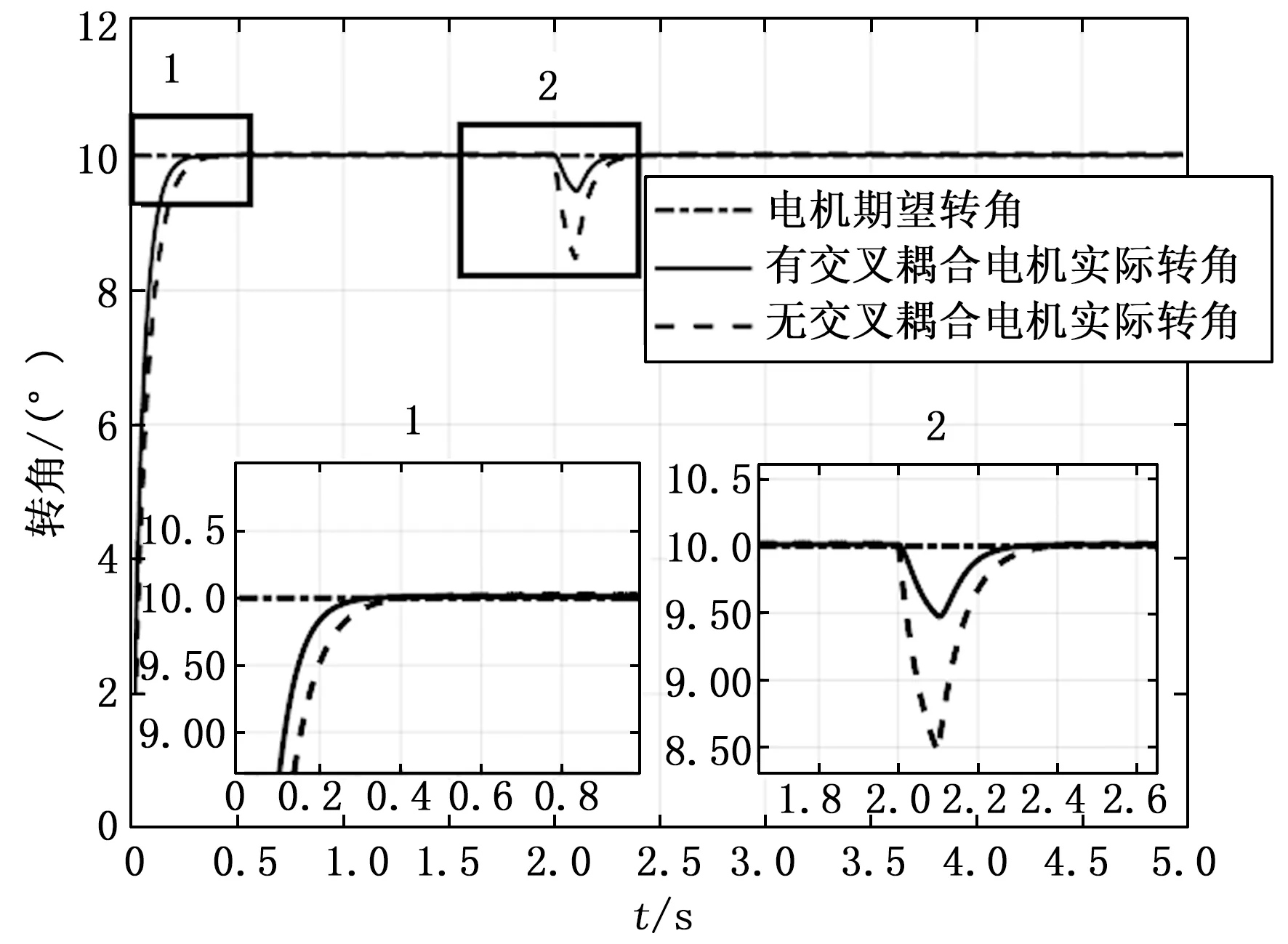
图13 转向电机存在干扰效果对比图

1)在相同的条件下，有交叉耦合控制效果优于无交叉耦合。在启动时瞬态响应上，有交叉耦合控制上升时间和调整时间均小优于无交叉耦合控制，有交叉耦合控制的上升时间为无交叉耦合控制的78.4%，调整时间为76.0%。

2)在突然受到外界负载的作用下，有交叉耦合控制转角最大波动仅为无交叉耦合控制最大波动的34.8%，故有交叉耦合控制抗干扰能力强；有交叉耦合控制的调整时间为无交叉耦合控制的调整时间的76.2%，调整时间仅为0.394 s，故该运动控制算法收敛速度快。

为了更好地模拟电机实际运行的状态，将目标转角设置为变幅值，在2.5 s加入干扰信号，分别得到4个转向电机的转角跟踪图14、跟踪误差图15和同步误差图16。如图14所示，转向电机响应快，无超调，抗干扰能力强。如图15和16所示，误差能在很快的时间内收敛到0，当电机受到外界干扰时，4个电机能在0.2 s内修正误差并能降低干扰信号对系统的影响，实现4个转向电机协同控制且控制系统具有较高的同步性和很强的抗干扰能力。

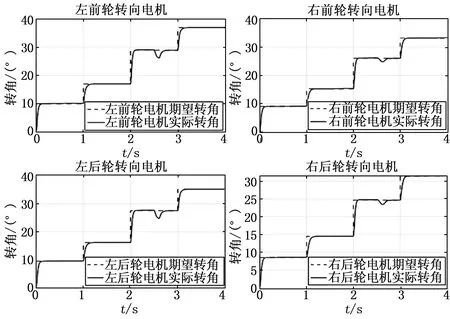
图14 4个转向电机的转角跟踪图

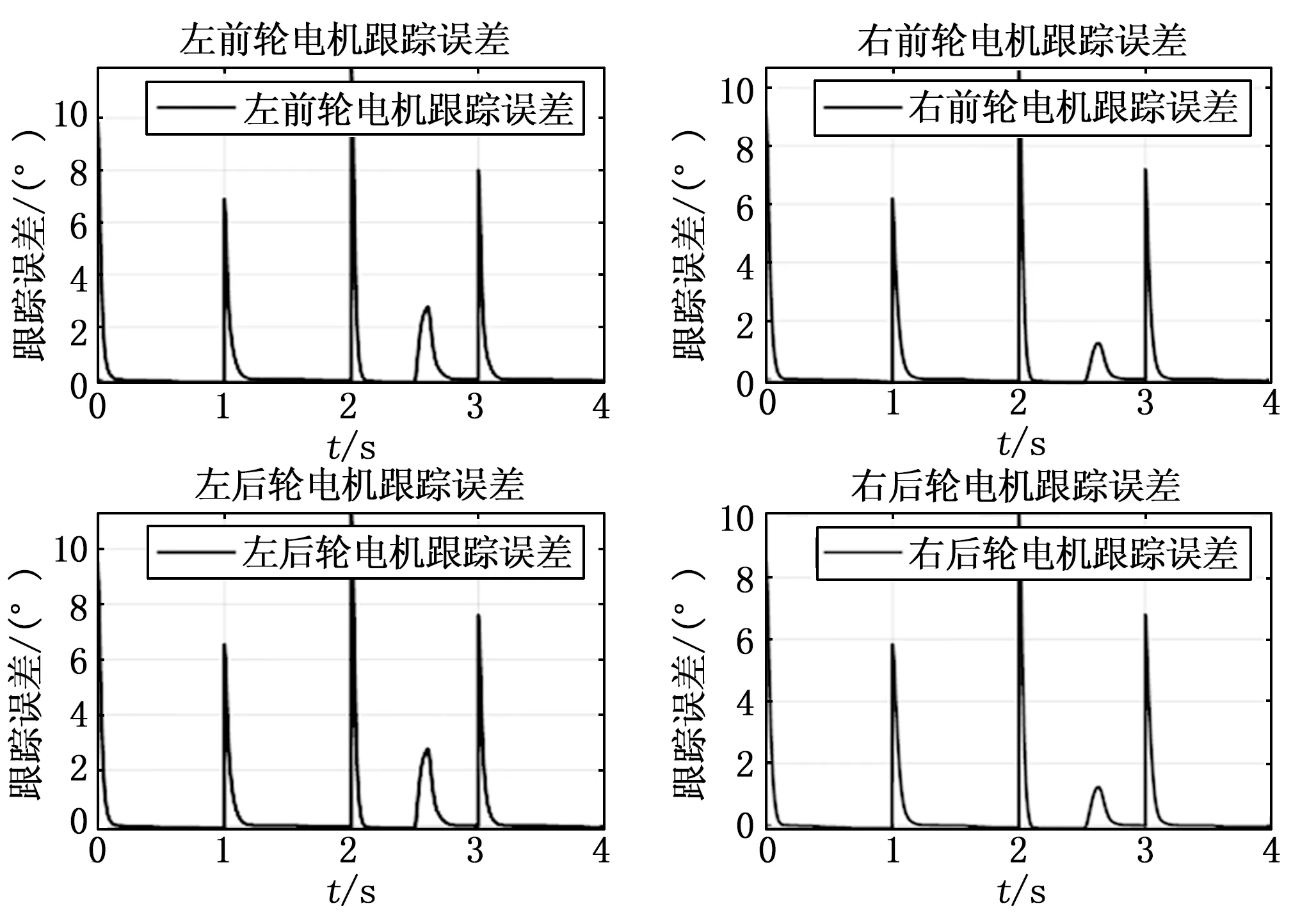
图15 4个转向电机的跟踪误差图

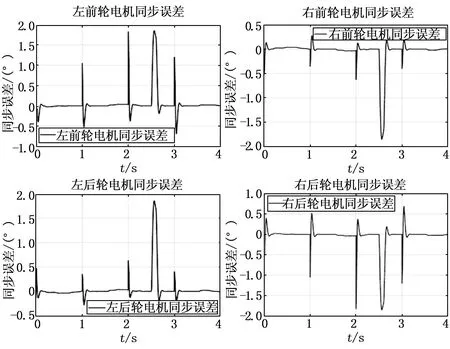
图16 4个转向电机的同步误差图

5 结束语

1)本文对四舵轮式全向重载AGV转向控制进行研究，根据四舵轮式AGV机械结构及运动学规律建立了四舵轮式AGV的数学模型；采用BAS-PID融合算法进行PID参数整定；同时运用了交叉耦合控制策略设计了位置补偿器。

2)BAS-PID融合算法能快速找出最优PID参数，使系统响应快且无超调，运用交叉耦合控制策略实现系统的高效协同。

3)仿真结果表明，系统同步性好，具有较强的抗干扰能力强，误差收敛速度快。当系统存在干扰信号时，系统调整时间快，所引起速度波动小，有效提高AGV的转向的同步性，扩大AGV的运用场合。