基于MSLSTM-DA模型的水质自动监测异常数据报警

嵇晓燕,姚志鹏,杨 凯,陈亚男,王 正,安新国

基于MSLSTM-DA模型的水质自动监测异常数据报警

嵇晓燕1*,姚志鹏1,杨 凯1,陈亚男1,王 正2,安新国2

(1.中国环境监测总站,北京 100012；2.北京金水永利科技有限公司,北京 100012)

提出一种基于多元堆叠长短时记忆网络-差值分析(MSLSTM-DA)模型对地表水质异常数据进行报警的方法.该方法首先建立MSLSTM模型对水质指标数据进行预测,再基于预测结果的残差分布建立DA模型,并确定各个指标的数据异常阈值,当实测数据与预测数据差值大于阈值时进行数据报警.以长江流域监测断面的水质数据进行了方法有效性验证.结果表明,构建的预测模型对５个指标的MAE、MAPE均值比BP神经网络预测模型降低21.0%,17.8%,比LSTM模型降低16.8%,17.9%.皮尔逊系数均值比BP神经网络、LSTM模型的分别高5.9%,4.4%.5个指标共检出水质异常数据37条,其中34条经人工判断确实存在有异常,报警准确率高达91.9%.

堆叠长短时记忆网络；差值分析；水质异常报警

地表水水质自动监测站作为监测地表水水质现状、及时预警潜在环境风险的重要基础,自1999年至今已建设了近3000个水质自动监测站,形成了覆盖我国十大流域和主要湖库的水质自动监测网络.自动监测站水质数据作为衡量国家地表水水质状况的基础数据,实时发现异常数据,从而预判水环境面临的风险具有重要意义[1].存在异常的水质数据很大程度上是由于环境污染造成的,因此实现水质异常数据的报警对实现水环境早期污染的预警预报有重要的支撑作用[2-4].

针对水质监测中异常数据的预警问题,许多学者做了大量的研究,也提出了多种基于不同原理的方法. 基于历史水质各个指标数据之间的关联性进行分析,如果当前时刻数据不满足相关性指标则判定为异常[5].因为数据相关性是基于多组数据进行计算的,对评判单一时刻的数据效果不太好,不适用于水自动站这种具有实时性要求的预警.再者就是利用统计学方法基于概率进行异常的判断[6],概率小的数据序列发生后则定义为异常数据.而基于概率进行数据异常判断的难点在于无法科学的衡量异常数据出现的概率,预警准确率难以保证.随着机器学习技术的快速发展,借助其强大的数据分析能力,也衍生出很多异常数据检测的方法[7-9].例如利用数据聚类的方法,对当前指标时间序列数据进行是否为离群点的检测,如果是离群点,则定义为异常数据[10].该方法适用于水质数据突变的异常检测,而对于趋势性的异常检测效果不好.通过机器学习模型对未来水质数据进行预测,然后根据监测值和预测结果的差值评判数据是否异常,这种方法依赖于预测模型的效果.基于传统的BP神经网络算法对历史数据进行训练,预测未来一段时间的水质指标数据值,当实测数据和预测值偏差较大时定义为异常数据等[11].但是上述方法忽略了水质监测数据序存在的时序性,因此影响预测模型的精度.

自动监测站水质监测数据作为反映水环境状况连续变化的数据序列,具有较强的周期性和自相关性,而且不同监测指标数据间也呈现很强的相关性.基于此,本文提出一种基于多元堆叠长短时记忆网络-差值分析(MSLSTM-DA)模型进行水质异常报警的方法,通过对监测指标历史时间序列数据进行学习,然后对预测残差进行分析确定阈值,实现对水质异常数据的报警.

1 模型建立

1.1 MSLSTM模型

图1 MSLSTM模型结构示意

长短时记忆神经网络(LSTM)模型是一种具有时间循环结构的神经网络模型,广泛应用于具有时间属性的数据序列的预测分析.在地表水环境监测中,同一断面的水质监测数据具有时间维度上的因果联系,适合采用长短时记忆神经网络进行预测分析[12-14].多元LSTM(MLSTM)是指模型输出的变量个数多于一个.对于自动监测站水质数据而言,因为监测指标较多,如果仅对单一指标进行建模,一是模型无法获取指标数据间的关联性;二是在实际的异常数据检测应用中,多个模型并行运行会导致计算效率较低.堆叠LSTM(SLSTM)模型是具有多个隐藏LSTM层的模型,每个层包含多个存储单元.该模型加大了模型深度,可以提取到水质监测数据序列中更深层次的特征,同时也增强了模型的预测能力[15-17].

本文采用的MSLSTM模型中包括4个LSTM层,其中添加BatchNorm层可以加速模型的训练, Dropout层有助于提高模型的泛化能力[18].模型输出的变量包括溶解氧(DO)、高锰酸盐指数(IMn)、氨氮(NH3-N)、总磷(TP)以及总氮(TN)等5个指标.相应的模型结构见图1.

1.2 DA模型

考虑到地表水环境的复杂性,影响水质的因素较多,因此水质预测数据与实测数据会存在合理偏差.差值分析(DA)模型是对水质指标的实际监测值与模型预测值的差值序列进行分析.当预测模型达到一定的预测精度后,模型的输出与实际值的差值序列应该是在0值上下波动,并关于0值呈现近似对称分布.基于此本文构建了一种基于迭代法计算差值阈值的流程.首先计算监测值和模型预测中差值的绝对值序列D,初始上限值U设置为0,置信水平设置为0.9,计算序列D中不大于上限值的占比,当该占比大于0.9时,则得到阈值;如果小于等于0.9,则增加初始上限值,直到得到该预测模型差值的阈值.DA模型结构见图2.

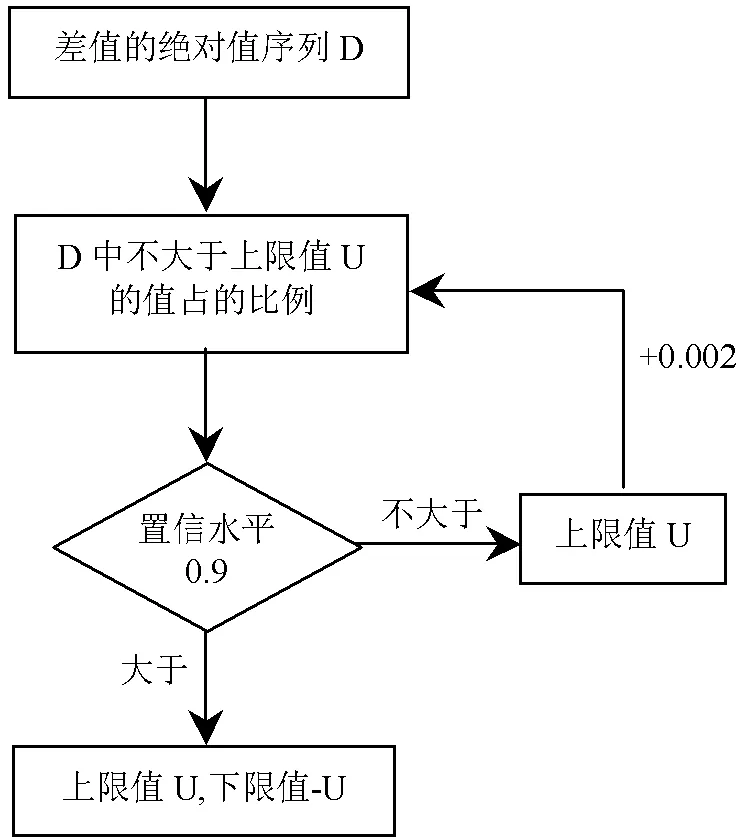
图2 DA模型结构

2 异常数据检测方法

基于MSLSTM-DA模型进行水质异常数据报警的流程包括构建模型数据集、训练MSLSTM模型、建立DA模型、模型效果评估以及异常数据实时报警.

2.1 构建模型数据集

利用临近值填充法对水质监测指标历史数据集中缺失的数据进行填充,形成预处理数据集.并根据监测数据的时间顺序以7:2:1的比例将预处理数据集分割为训练、验证与测试数据集,并根据训练数据集中各个指标的最大、最小值对这3个数据集的对应指标进行Min-Max归一化,将数据转换到01之间.

2.2 训练MSLSTM模型

根据训练数据集对MSLSTM模型进行训练,训练迭代次数设置为10000次,神经网络优化器选择Adam,模型最后一个全连接层的激活函数选择sigmoid.通过实时判断验证数据集的预测效果提前结束训练,防止过拟合.在模型训练完成后,分别将训练、验证数据集作为模型的输入数据得到相应的模型预测值.

模型训练完成后,需要对模型预测的精确度进行评估.本文采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、皮尔逊相关系数对模型进行评价.

2.3 建立DA模型

计算水质监测指标监测值和模型预测值之间的差值,并对差值序列进行关于0值对称分布检验.如果通过检验,则建立DA模型,根据置信水平得到水质异常区间以及水质异常阈值.否则更改模型结构和参数再次进行模型的训练.

2.4 模型效果评估

针对预测数据集计算模型预测值,根据预测值和监测值之间的差值以及得到的水质异常数据阈值,进行异常数据的检测,当检测出来的数据的确为异常数据时,说明模型可以应用于实际的水质异常数据检测.否则的话则重新设置差值分析模型的置信水平.

2.5 异常数据实时报警

获取当前时刻水质自动监测数据的实时监测值,并计算模型对该时刻水质的预测值,当实测值和模型预测值得差值超过异常阈值时,确认当前时刻水质监测值为异常数据并报警,否则为正常数据.

图3 MSLSTM-DA模型水质异常数据检测流程

3 实例验证

3.1 数据集说明

选择位于长江流域某一断面2019-01-01至2020-12-31的水质自动站监测数据,共4386条.因为DO的监测频率为1次/h,而其他指标为1次/4h,构建模型数据集需要统一时间粒度,因此DO选择和其他指标相同的监测时刻数据(表1).

表1 数据条数表

水质监测数据具有时间属性,前后时刻的数据呈现很强的相关性,因此选择利用临近值填充的方法对缺失的指标数据填充,不会影响水质数据序列的时序性.按照时间顺序将预处理数据集按照7:2:1的比例分割为训练、验证、测试数据集(表2).

表2 模型数据集

当前监测时刻以及前11个监测时刻的5指标数据作为模型的输入数据.当LSTM这类神经网络在学习时间序列数据的规律时,因为时间序列存在自相关性,神经网络会将前一时刻的数据当作当前时刻的预测值,导致最后的预测序列出现时间延迟现象.因此本文将当前时刻水质数据减去前一个监测时刻的5指标水质数据的差值数据作为模型的输出数据.

3.2 MSLSTM模型结果分析

模型训练完成后,对训练、验证和测试数据集进行预测结果的评估.精确度评估表见表3.

表3 MSLSTM模型精确度评估表

表4 三种模型精确度评估表

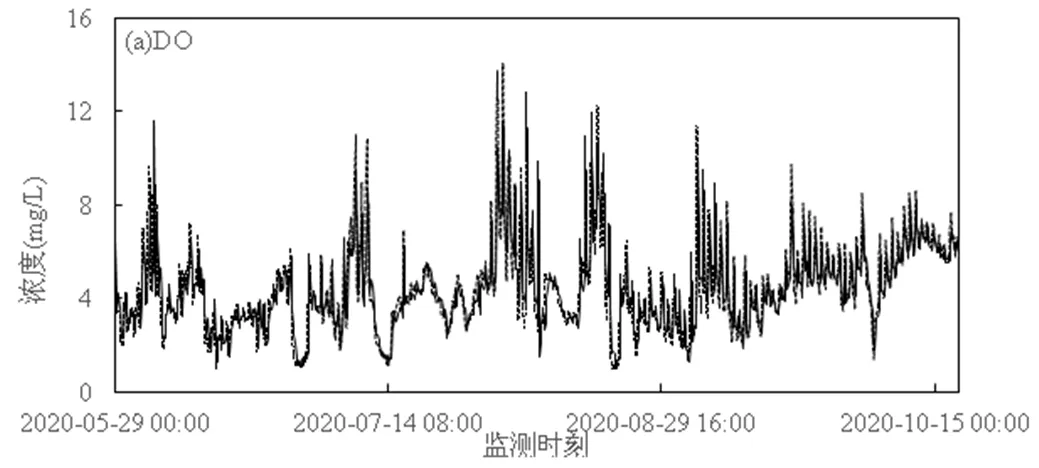
由精确度评估结果(表3)可以看出,指标MAE对于各指标的数据范围而言,都比较低;指标的MAPE均在20%以下,说明数据预测的精确度达到了80%以上;皮尔逊相关系数均大于0.8,说明预测结果序列和监测值序列的线性趋势关系较强.从测试数据集的模型预测值和监测值的对比曲线(图4)可以看出,各个指标的预测值和监测值的曲线贴合度较高.为进一步说明本文构建的预测模型的有效性,选择BP神经网络[19]、LSTM模型[20]作为对照模型.

由三种模型在测试数据集上的对比结果(表4)可以看出,本文构建的预测模型的5个指标的MAE、MAPE均值比BP神经网络预测模型降低21.0%,17.8%,比LSTM模型降低16.8%,17.9%.皮尔逊系数均值比BP神经网络、LSTM模型的高5.9%,4.4%,表明本文构建的预测模型对各个指标的预测精确性比较高.

3.3 建立DA模型

计算验证数据集的预测值,并绘制预测值与指标监测值差值的直方图,并进行阈值计算.

图5 5个水质监测指标的差值分布

Fig.5 Difference distribution charts

从图5可以看出,5个指标的差值序列主要集中在0值附近,并关于0值近似呈现对称分布.

3.4 异常数据报警验证

基于DA模型得到的数据异常阈值,对测试数据集进行异常数据检测.5指标共检测异常数据37条,其中IMn6条,NH3-N12条,TP8条,TN 11条,DO并未发现异常数据.异常数据见图6.

对检测出的异常数据进行人工核查,发现34条数据存在异常的可能性较大,异常数据检出正确率达到91.9%,并且不存在异常数据的遗漏情况.说明此方法可以应用于水质自动监测数据管理的异常数据报警.

4 结论

4.1 本文提出的多元堆叠长短时记忆网络模型,可消除异常值以及缺失值对预测模型的影响,可实现地表水水质数据的预测,精确度达到了80%以上,为进一步提升水环境质量提供了依据.

4.2 通过预测数据的残差分布建立差值分析模型,得到判定水质数据异常的阈值.基于该阈值以及预测数据对当前时刻水质监测数据进行异常判定,预警准确率可达90%以上.

[1] 邢梦林,王潇磊,郑 瑶,等.浅谈水质自动监测系统的建设及应用研究 [J]. 环境科学与管理, 2013,(10):40-42.

Xing M L, Wang X L, Zheng Y, et al. Discussion on construction and application of water quality automatic monitoring system [J]. Environmental Science and Management, 2013,(10):40-42.

[2] 嵇晓燕,刘廷良,孙宗光,等.国家水环境质量监测网络发展历程与展望 [J]. 环境监测管理与技术, 2014,26(6):1-4,8.

Ji X Y, Liu T L, Sun Z G. The Development of water environmental quality monitoring network in China [J]. The Administration and Technique of Environmental Monitoring, 2014,26(6):1-4,8.

[3] 计 红,韩龙喜,刘军英,等.水质预警研究发展探讨 [J]. 水资源保护, 2011,27(5):39-42.

Ji H, Han L X, Liu J Y, et al. Study on water quality early warning [J]. Water Resources Protection, 2011,27(5):39-42.

[4] 王文宝,曹 骞.水质自动监测站的运行管理与水质预警 [J]. 环境监控与预警, 2010,2(1):54-56.

Wang W B, Cao Q. Operation of automated water quality monitoring stations and water quality prewarning [J]. Environmental Monitoring and Forewarning, 2010,2(1):54-56.

[5] 周 纯,张 苒.水质自动监测异常数据的分析与利用[J]. 新疆环境保护, 2012,34(4):42-44.

Zhou C, Zhang R. Analysis and application of water quality outlier automatic monitoring [J]. Environmental Protection of Xinjiang, 2012,34(4):42-44.

[6] 王 威,沈兴厚,张利亚.皮尔逊Ⅲ型频率曲线在水源地水质预警中的应用 [J]. 河南科学, 2018,36(7):1042-1048.

Wang W, Shen X H, Zhang L Y. Application of pearsonⅢ frequency curve on water quality warning of water source [J]. Henan Science, 2018,36(7):1042-1048.

[7] Huang X. Abnormal data detection technology based on improved neural network [J]. International Journal of Applied Mathematics and Soft Computing, 2018,7(1):89-94.

[8] Liu F, Su W X, Zhao J J, et al. Abnormal data detection method based on fuzzy autoregressive hidden markov Model [J]. Journal of Residuals Science & Technology, 2016,13(8):38-45.

[9] 李若楠,王 琦,刘书明.基于典型相关系数和随机森林的水质预警方法 [J]. 中国环境科学, 2021,41(9):4457-4464.

Li R N, Wang Q, Liu S M. Water quality warning method based on canonical correlation coefficient and random forest [J]. China Environmental Science, 2021,41(9):4457-4464.

[10] 梅 林,张凤荔,高 强.离群点检测技术综述 [J]. 计算机应用研究, 2020,37(12):3521-3527.

Mei L, Zhnag F L, Gao Q, et al. Overview of outlier detection technology [J]. Application Research of Computers, 2020,37(12): 3521-3527.

[11] 史 斌,姜继平,王 鹏.基于高频在线水质数据异常的突发污染预警 [J]. 中国环境科学, 2017,37(11):4394-4400.

Shi B, Jiang J P, Wang P. Early warning of water pollution incidents based on abnormal change of water quality data from high frequency online monitoring [J]. China Environmental Science, 2017,37(11): 4394-4400.

[12] Palani S, Liong S Y, Tkalich P. An ANN application for water quality forecasting [J]. Marine Pollution Bulletin, 2008,(56):1586-1597.

[13] Liu J J, Zhuang H, Tie Z X, et al. Water quality multi-factor prediction model using LSTM neural network based on K-similarity noise reduction [J]. Computer Systems Applications, 2019,28(2):226-232.

[14] Li X, Peng L, Yao X J, et al. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation [J]. Environmental Pollution, 2017,231:997-1004.

[15] 王 军,高梓勋,朱永明.基于CNN-LSTM模型的黄河水质预测研究 [J]. 人民黄河, 2021,43(5):86-99.

Wang J, Gao Z X, Zhu Y M. Research on Yellow River water quality prediction based on CNN-LSTM Model [J]. Yellow River, 2021, 43(5):86-99.

[16] 刘建华,李锦程,杨龙月,等.基于EMD-SLSTM的家庭短期负荷预测 [J]. 电力系统保护与控制, 2019,47(6):40-47.

Liu J H, Li J C, Yang L Y, et al. Short-term household load forecasting based on EMD-SLSTM [J]. Power System Protection and Control, 2019,47(6):40-47.

[17] Wu Q F, Meng X Y, Liu M Y. Prediction of rice yield via stacked LSTM [J]. International Journal of Agricultural and Environmental Information Systems (IJAEIS), 2020,11(1):86-95.

[18] 杨 青,王晨蔚.基于深度学习LSTM神经网络的全球股票指数预测研究 [J]. 统计研究, 2019,36(3):65-77.

Yang Q, Wang C W. A study on forecast of global stock indices based on deep LSTM neural network [J]. Statistical Research, 2019,36(3): 65-77.

[19] 张秀菊,王柳林,李秀平,等.基于BP神经网络的潇河流域水质预测 [J]. 水资源与水工程学报, 2021,32(5):19-26.

Zhang X J, Wang L L, Li X P, et al. Water quality prediction of the Xiaohe River Basin based on BP neural network model [J]. Journal of Water Resources and Water Engineering, 2021,32(5):19-26.

[20] 张贻婷,李天宏.基于长短时记忆神经网络的河流水质预测研究 [J]. 环境科学与技术, 2021,44(8):163-169.

Zhang Y T, Li T H. River water quality prediction based on long short-term memory neural network [J]. Environmental Science and Technology, 2021,44(8):163-169.

Water quality alert with automatic monitoring data based on MSLSTM-DA model.

JI Xiao-yan1*, YAO Zhi-peng1, YANG Kai1, CHEN Ya-nan1, WANG Zheng2, AN Xin-guo2

(1.China National Environmental Monitoring Center, Beijing 100012, China；2.Golden Water Technology (Beijing) Ltd, Beijing 100012, China)., 2022,42(4)：1877～1883

A multivariate stacked long and short term memory network-difference analysis (MSLSTM-DA) model is proposed to alarm surface water quality abnormal data. Established the MSLSTM model to predict the water quality data, and then established the DA model based on the residual distribution of the prediction results to determine the threshold value of each indicator, and alerted the data when the difference between the measured data and the predicted data is greater than the threshold value. The validity of the method was verified using water quality data from the Yangtze River basin monitoring sections. The results showed that the mean values of MAE and MAPE for five indicators were 21.0% and 17.8% lower than those of BP neural network prediction model, and 16.8% and 17.9% lower than those of LSTM model. The mean value of Pearson coefficient was 5.9% and 4.4% higher than that of BP neural network and LSTM model. 37 abnormal water quality data were detected for the 5 indicators, 34 of which were judged to be abnormal by manual judgment, with an alarm accuracy rate of 91.9%.

stacked long and short-term memory network；difference analysis；water quality alert

X832

A

1000-6923(2022)04-1877-07

嵇晓燕(1981-),女,江苏淮安人,正高级工程师,博士,主要研究方向为水环境质量监测评价.发表论文30余篇.

2021-09-18

长江生态环境保护修复联合研究项目(2019-LHYJ-01-0301);国家水环境监测监控及业务化平台技术研究课题(2017ZX07302002)

*责任作者, 正高级工程师, jixy@cnemc.cn