2021年广州市中考数学压轴题的变式研究

广东省广州市执信中学(510062)刘玲

1 试题呈现

如图1,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.

图1

(1)当点E运动到AB中点时,证明: 四边形DFEC是平行四边形;(2)当CG=2 时,求AE的长;(3)当点E从点A开始向右运动到点B时,求点G运动路径的长度;

注: 此题第(1)问较为简单,第(2)问主要运用好60°这个条件,构造直角三角形,运用勾股定理列方程即可,笔者这里只针对第(3)问进行解答及变式探究.

图2

2 试题解答

法一纯几何法

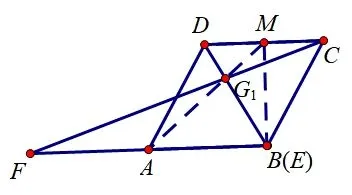
图3

图4

法二建立平面直角坐标系

3 解后反思

3.1 背景分析

此题笔者主要呈现了两种解题思路,仔细分析,此题实质上是找点G的运动轨迹,如果能够找到点G的轨迹,那么问题就迎刃而解.但反观在中考考场上,能解答出来的同学少之又少.当然一方面与考试时间有关,但大多数是无从下手,大部分同学感觉迷茫,不知如何找到求点G轨迹的突破口.细看此题,此题的背景其实就是相似图形中最常见的“8 字型”相似,只是此题将图形放在菱形中,借助菱形的对边互相平行这一性质得到“双8 字型”相似,图中点E,F为动点,点A为定点,且为EF的中点,那么直线AG交直线CD为定点,且为CD的中点.这样就能确定点G的运动轨迹为线段“AM”.

补充“双8 字型”相似结论: 如图5,若CD//EF,则.

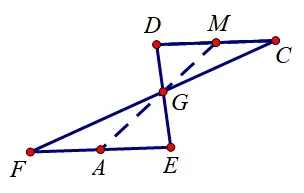
图5

3.2 两种解法对比分析

若实在没有找到隐藏的“双8 字型”相似,也可以采用建立平面直角坐标系的方法,采用代数运算的方式找到动点G的轨迹方程,发现其为一次函数,说明其在直线上运动,然后再去找临界值也可将问题解决.

对比几何方法和建系的方法,我们可以发现: ①几何方法思维含量高,较难找到突破口,但一旦找到突破口,复杂问题就会被转为成我们熟悉的几何问题上去; ②建系方法好想,没有太多的思维含量,但是采用此种方法不免会带来繁杂的计算量,因此,采用此种方法的前提是必须要有很强的计算功底,否则,不要轻易尝试.此种方法适用于几何方法确实找不到突破口时,无从下笔时,不妨考虑此种方法,一般情况下,正方形,矩形,含特殊角的菱形,等边三角形等都可用建系的方法去解答问题.但若所求动点轨迹为圆时,初中生是无法识别圆的轨迹方程的,此时此种方法不太适用.其实,中考中求动点的轨迹无外乎两种类型,一种是直线型,另一种是圆弧形.因此在做题时,我们可以通过观察比如找特殊点等大致猜测此动点的轨迹是否为直线.

4 变式推广

4.1 横向联想——类比推广

联想1改变条件“菱形”为“正方形”

变式1如图6,在正方形ABCD中,AB=2,点E为直线AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.当点E从点A开始向右运动到点B时,求点G运动路径的长度.

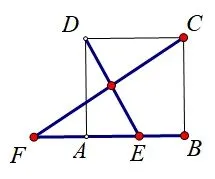
图6

此题解法仍可采用上述两种方法,读者可以自行完成.此外,还可以改为“矩形”,“平行四边形”等,解法基本一致.通过以上变式,发现,只要提供一组对边平行即可,因此可以弱化条件,将其改为“一组对边平行的四边形”,于是就有了以下联想.

联想2改变条件“菱形”为“梯形”

变式2如图7,在梯形ABCD中,AB=4,AD=BC=3,CD=1,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.当点E从点A开始向右运动到点B时,求点G运动路径的长度.

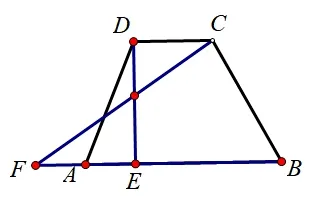
图7

4.2 纵向迁移,归纳推广

联想3改变条件“AF=AE”为“AF=2AE”

变式3如图8,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=2AE,且CF、DE相交于点G.当点E从点A开始向右运动到点B时,求点G运动路径的长度.

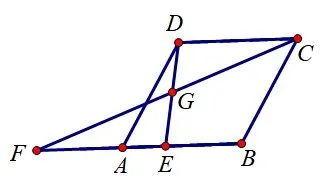
图8

联想4改变条件“AF=AE”为“AF=nAE”

变式4如图9,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=nAE,且CF、DE相交于点G.当点E从点A开始向右运动到点B时,求点G运动路径的长度(用含n的字母表示).

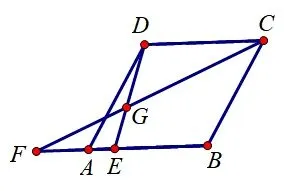
图9

以上2 个变式从纵向进行了推广,改变数量关系,仍可采用原题的两种解法,由特殊到一般,层层递进,但实质没变,仍为“双8 字形型”相似,推导出更为一般性的结论.

4.3 变式拓展,掌握本质

联想5改变设问方式

变式5如图1,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.求CG+EG的最小值.

变式5 改变了设问方式,难度稍有增加,想解决此问题仍然需要先找到点G的运动路径,从而发现此题实质上是一个将军饮马问题,那么问题也将迎刃而解.

联想6变构造元件

变式6如图10,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且直线CE、DF相交于点G.求CG的最小值.

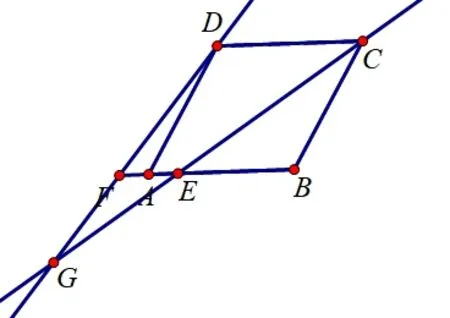
图10

变式6 主要改变了点G的生成方式,看上去与原题发生了改变,但仔细分析,还是有一定的联系,只是由原来的“双8 字型”相似变为了“双A 字型”相似,点G仍然是在原直线AM上运动,只是不包括线段AM这一部分,在两条射线上运动,那么,求CG的最小值可利用“点到直线的距离,垂线段最短”求解出.

联想7变关联结构

变式7如图11,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,点F为CD上一动点,且CF=2AE,过点D作DG⊥EF于点G,求CG的最小值.

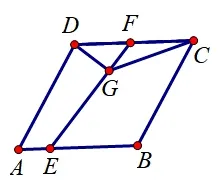
图11

变式7 与2021年广州市一模第25 题如出一辙,基本背景是“8 字型”相似,连接AC与EF交于点H,则H为定点,则点G在以DH为直径的圆上运动,则CG的最小值即可求解出来.

5 教学启示

罗增儒教授曾经说过[1]:“解决问题的本质是思维活动的过程,通过典型例题的分析能启迪学生的思维,提高解题能力.”ACT-R 理论指导的深度教学认为练习一定要进行变式,通过变式训练,在“变”中找到“不变”的规律,从而搞清问