伸缩变换在椭圆问题中的应用与拓展——从一道教材习题的解法谈起

云南省下关第一中学(671000) 马孟华

伸缩变换作为高中阶段学习的重要内容,经常出没于高考试题中.本文结合对教材课后习题的解法探究,深入拓展总结出了“伸缩变换”在解决椭圆问题上的方法优势,并对伸缩变换的几个重要性质作了介绍.

1 利用伸缩变换解决椭圆中的定值、最值、范围问题

1.1 问题的提出

例1 (人教A 版《数学》(选修4-4) 第15 页习题1.3第6 题) 已知椭圆的中心为O,长轴、短轴的长分别为2a,2b(a>b>0),A,B分别为椭圆上的两点,且OA⊥OB.

(2) 求∆AOB面积的最大值和最小值.

分析因为该题出现在“简单曲线的极坐标方程”后的习题,考虑该题在教材中的“位置背景”,自然想到用极坐标方程解决.

解决上述问题的方法看似自然,但在实际教学过程中,往往令人大失所望.问题主要出现在第(2)问的解答过程中,计算和化简过程及其复杂,特别是由表达式到化简的过程是绝大多数学生无法完成的.

1.2 解决椭圆中三角形面积的最值、范围问题

例1 的“位置背景”明显,显然优先考虑“极坐标法”.但我们不应忽视这样一个事实:学生在脱离“位置背景”的情况下独立解决问题(如考场上遇到这类问题),是不容易“对号入座”的,在没有“位置背景”的支撑下,如何整合日常所学找到解决问题的有效手段? 定位有效方法? 最终提升解题速度和解题能力,这应该是一线教师在课堂教学中最应该重视的一个问题,即一线教学经常探讨的课题——课堂教学的有效性和整合性.在结合具体的教学实际以及深入研究后,我们可以考虑使用平面中的“伸缩变换”方法来解决该问题.解法如下:

图1

图2

如果我们在一线教学中抛开数学问题的“位置背景”,在教学过程中不局限于局部性问题特征,有效的将教学内容和问题进行整合分析,防止“碎片化”教学情况的发生,提升教学内容、方法、思想的完整性,从而增进课堂教学的有效性.

1.3 解决椭圆中的距离、弦长问题

实际上,我们也可以利用伸缩变换解答第(1)问.

事实上,在伸缩变换作用下,椭圆上任意两点构成的线段在变换前后的长度关系是可以确定的,此问中涉及了比较特殊的原点到椭圆上动点的距离问题,但其可以推广到一般化的变换前后椭圆上两点间距离或弦长间的关系问题,其理论基础就是伸缩变换前后斜率比值关系的不变性,利用斜率比值的不变性可以寻求弦长间的比值关系.推导如下:

2 伸缩变换的定义及常用性质

2.1 伸缩变换的定义

2.2 伸缩变换下的常用性质拓展

即可解释为:伸缩变换前后对应的直线的斜率比不变、平行线段长度比不变、多边形面积比不变,这些不变量和不变性为初等几何的一些问题的解决提供了新的方法,使得椭圆中的定值、范围、最值问题转化为了单位圆中的简单问题,从而使解析几何中难题的解决变得更为直观和快捷.

3 伸缩变换方法的再应用

3.1 伸缩变换在竞赛试题中的应用

3.2 伸缩变换在高考试题中的应用

例3 (2018 年高考新课标II 卷理科第22 题)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).

(1)求C和l的直角坐标方程;

(2)若曲线C截直线l所得线段的中点坐标为(1,2),求l的斜率.

解析(1)曲线C的直角坐标方程为=1.当cos0 时,l的直角坐标方程为y=tanα·x+2−tanα,当cosα=0 时,l的直角坐标方程为x=1.

(2)的解法1 设直线l与曲线C交于A,B两点,将l的参数方程代入曲线C的直角坐标方程,整理得关于t的方程:

(1)求C的方程;

(2)点N为椭圆上任意一点,求∆AMN的面积的最大值.

解析(1)C的方程为=1,过程从略.

图3

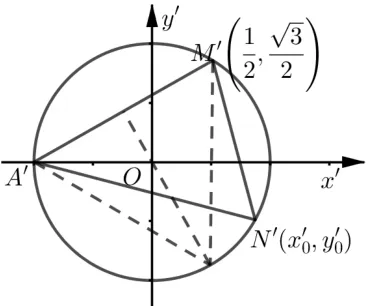
图4

评析在伸缩变换的条件下,椭圆中的三角形面积的最值问题,转化为了单位圆中三角形面积的最值问题,此时在单位圆中的最值问题可以采用“数形结合”解决,从而规避了椭圆中的复杂代数运算,使得问题的解决变得简单有效和快捷.

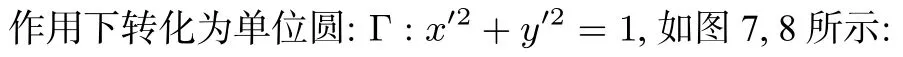
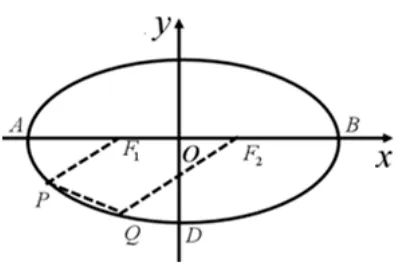
图5

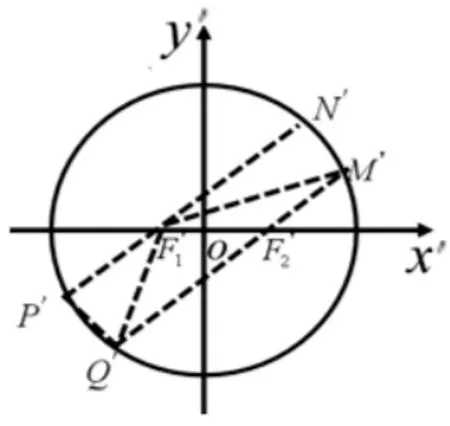
图6

本文只例举了几个例子加以说明,再如:2008 年高考全国Ⅱ卷理科第21 题,2013 年高考全国新课标Ⅱ卷理科第20题,2014 年高考全国新课标Ⅰ卷理科第20 题,2015 年高考全国新课标Ⅱ卷理科第20 题,2015 年高考陕西卷理科第20 题等等均可用伸缩变换解决,且规避了复杂和繁琐的代数运算.值得注意的是,伸缩变换作为一种有效的解决椭圆中直线斜率、弦长、多边形面积问题的有效工具,不仅可以规避解析几何中复杂、繁琐的代数运算,而且在一定程度上还能带领我们领略命题者的命题意图,带领我们掌握数学问题的来源和本质,最终我们也能像命题专家一样依据问题的本质命制新的试题.

当然,作为解决解析几何中椭圆问题的有效工具,其局限性也是存在的,比如,涉及双曲线、抛物线问题时,伸缩变换的优势就不明显了,从目前新课程中对高中数学学科核心素养的要求以及高考考查的目标方向来看,圆锥曲线的考查是综合的,且灵活多变的,建议教师教学的主要手段还是应该回归到解决数学问题的“通性通法”上来,在提升学生解题能力、思维能力的同时,带领体会知识的生成过程,掌握数学问题的本质,这样也才能更好的在教学中落实好培养学生数学学科核心素养的根本目标.