一道课本例题的探究与拓展——巧用“等和线”妙解向量题

湖北师范大学附属中学(黄石一中)(435000) 杨瑞强

一、问题引入

人民教育出版社编写的普通高中教科书《数学》必修第二册第26 页例1 是这样的:

根据教材中这个问题的探讨,我们不难发现这样一个结论:

由三点共线定理可知,若λ+µ=1,则点C的轨迹是直线AB.于是,我们自然会思考:若λ+µ1,则点C的轨迹又是什么呢? 通过进一步探究,我们可以发现更多结论.

图1

二、问题探究

探究2 如图3 所示,在探究1 的条件下,过点C作直线l//AB,在l上任取一点C′,连接OC′交AB于点D′,则λ,µ,k又满足什么关系?

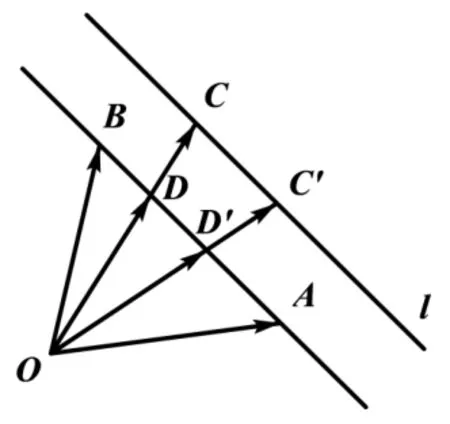
图3

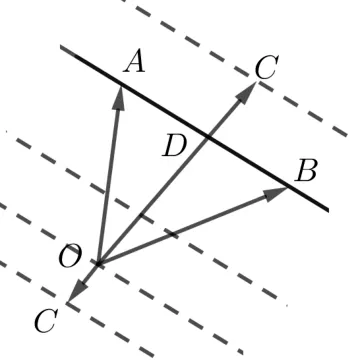
图4

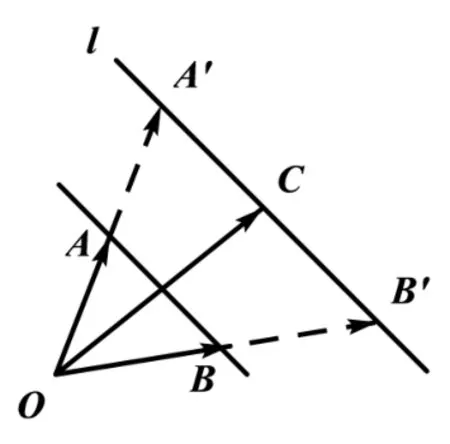
图5

三、向量等和线定理

根据上述问题的探究与分析可知,向量的等和线有如下结论:

我们运用“等和线”这一概念时,经常涉及下述性质:

(1)当等和线恰为直线AB时,k=1;

(2)当等和线在O点和直线AB之间时,k ∈(0,1);

(3)当直线AB在O点和等和线之间时,k ∈(1,+∞);

(4)当等和线过O点时,k=0;

(5)若两等和线关于O点对称,则定值k互为相反数;

(6)定值k的变化与等和线到O点的距离成正比.

四、向量等和线定理的妙用

“等和线”定理是专门解决有关基向量中系数之和的秒杀工具,对于处理向量分解时的系数之和以及系数最值有关问题,均可以尝试使用向量“等和线”定理.下面分类加以说明向量“等和线”定理的妙用.

类型1:基底起点相同

1.求共起点向量线性运算的系数和

根据等和线求共起点向量线性运算的系数和的步骤:(1)确定值为1 的等和线;(2)平移(旋转或伸缩)该线,作出满足条件的等和线;(3)从长度比或点的位置两个角度,计算满足条件的等和线的值.

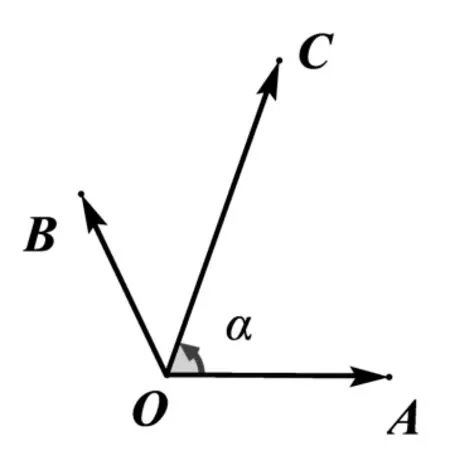
图6

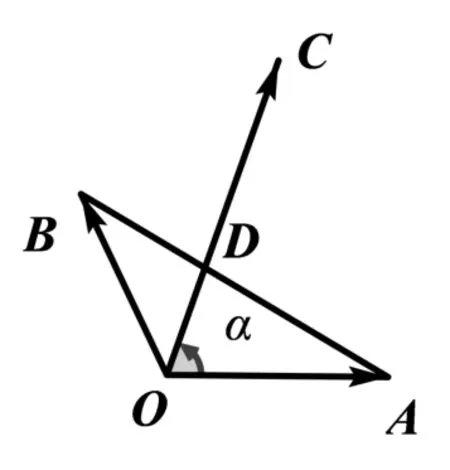
图7

2.求共起点向量线性运算系数和的最值(范围)

根据等和线求共起点向量线性运算系数和的最值(范围)的步骤:(1)确定值为1 的等和线;(2)平移(旋转或伸缩)该线,结合动点的可行域,分析何处取得最大值和最小值;(3)从长度比或点的位置两个角度,计算最大值和最小值.

解析如图8 所示,由平面向量的等和线定理可知,当等和线l与圆相切时λ+µ最大,此时λ+µ==3.故选A.

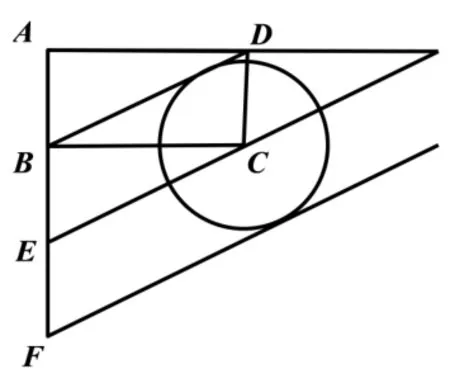
图8

评析对于动向量问题,如果向量的终点不在等和线上,则这类问题往往涉及求系数和的最值或者范围.对于这类问题,可转化为线段比值的最值或者范围问题来解决.

3.求向量线性运算的系数的线性关系式的最值(范围)

在利用等和线定理求解两系数的线性关系式的值时,需要先通过变换基底向量,使得需要研究的代数式为基底的系数和,再去找基底向量的等和线,转化为线段比例关系求解.要只需OD最小,即当OD是∆OMN的高时最大,经计算可得OD=所以3x+5y的最大值是.故选A.

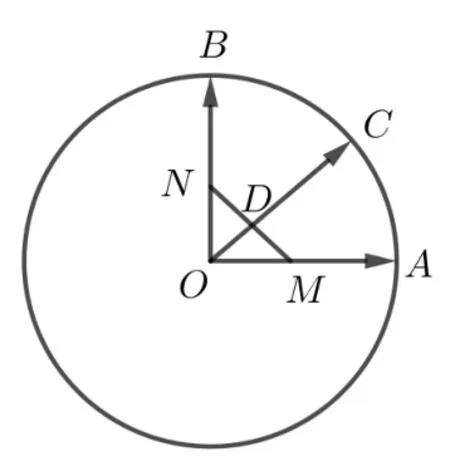
图9

评析当有的等和线问题并不是直接求向量系数和的值或最值时,而是求类似于λx+µy(其中λ,µ为常数)这种形式的相关问题,此时可以转化为两个新向量的等和线问题来解决.

类型2:基底起点不同

运用等和线定理时,需要注意三个向量应该共起点,对于不是共起点的问题,可通过找相等向量,从而把相关问题转化为等和线问题.

图10

评析本题中的三个向量并不是共起点的,而平面向量共线定理表达式中的三个向量的起点一致,此时可以将向量平移实现起点重合.

类型3:基底一方或两方可变

对于动向量问题,向量的终点不在等和线上求系数和的最值或者范围时,可转化为线段比值的最值或者范围问题来解决.

例5 在正方形ABCD中,如图11 所示,E为AB中点,P以A为圆心,AB为半径的圆弧上的任意一点,设则x+y的最小值_____.

图11

图12

评析当基向量的终点是变化的,使系数和λ+µ=1的等和线也是变化的,所以满足条件的等和线也相应保持平行变化,从而求解问题的关键在于探求保持平行变化中满足条件的等和线位置.

例6 如图13 所示,在平行四边形ABCD中,M,N为CD的三等分点,S为AM与BN的交点,P为边AB上一动点,Q为三角形SMN内一点(含边界),若则x+y的取值范围是_____.

图13

图14

评析平面向量共线定理的表达式中的三个向量的起点务必一致,若不一致,本着少数服从多数的原则,优先平移固定的向量;若需要研究两系数的线性关系,则需要通过变换基底向量,使得需要研究的代数式为基底的系数和.

类型4:基底可以合理调节

有时候所要求解的量是系数的一般线性关系式,而非系数和,考虑到可以通过数乘运算将向量进行同向或者反向伸长、压缩,所以从理论上讲,所有系数的线性关系式都可以通过合理调节向量的基底,将所求系数的线性关系式变为两个新的基向量的系数和.

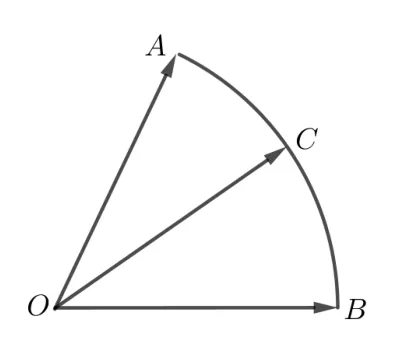
图15

图16

总之,向量的等和线巧妙地将代数问题转化为图形关系问题,将系数和的代数式运算转化为了距离的比例运算,数形结合思想得到了有效直接的体现.向量的等和线法将复杂的不等式问题、范围问题、数量积问题转化为简单、直接、操作方便的点到直线距离问题,很多时候用相似即可迅速解决.因此,等和线在解决平面向量中双变量代数式求取值范围或最值问题时,具有得天独厚的优势.