风机变极调速主回路选用分析

尤士刚

(华通设计顾问工程有限公司，北京 100034)

0 引言

在设计实践中，通风专业经常会采用“双速风机”的作法，如在平时用于排风而在消防时用于排烟的两用风机，就是采用“双速”的作法来实现两种工况下的设计目标(风量、风压)。但双速风机的主回路应采用何种接法应做认真评估。

哪种主回路接法适合于风机变极调速？两种工况下的功率比与接法是否有对应关系？此类问题一直未引起应有的重视，也没有相关的论文对此进行论述。

本文依据机座号与转速及功率的对应关系给出接线形式的选择方法，同时依据电机学的基本原理，通过对交流异步电动机的特性分析及风机负载特性分析，总结归纳出常用风机变极调速接线形式的特点及应用指引(如根据功率比确定接线形式)，推论出适合于双速风机的接线形式。

1 通过“功率比”确定主接线

1.1 主接线

交流异步电动机设计制造时可通过对三相定子绕组的不同布放处理、设置绕组的引出线端头数量等方法来实现不同的同步转速，进而实现“变极调速”的目的。绕组接法有多种，如用于双速的△/YY、Y/YY、Y/Y接法，用于多速的Y/△/YY、△/Y/YY、△/△/YY/YY、Y/Y/YY接法等。

1.2 机座号与转速及功率的对应关系

对电动机的主要技术条件，机械行业内有明确的标准，如《YD系列(IP44)变极多速三相异步电动机技术条件(机座号80～280)》JB/T 7127-2010、《YDT系列(IP44)JB/T 8681-2013变极多速三相异步电动机技术条件(机座号80～315)》。

表1为笔者整理的常用接法下的机座号与转速及功率的对应关系。设计人员可以根据表1中的功率值查出接线方法，如功率比为2.7/12的电动机，主回路为Y/YY接线；功率比为6.5/13的电动机，主回路为Y/Y接线。

2 与风机调速有关的几个基本概念

在电机学领域，电机划分为直流电机、交流电机(包括同步电机与感应电机，变压器可视为具有整距绕组的感应电机)。在民用建筑领域，风机、泵类应用最为广泛，均属感应电机(亦称为交流异步电动机)的范畴。本节介绍与异步电机相关的几个相关知识点。

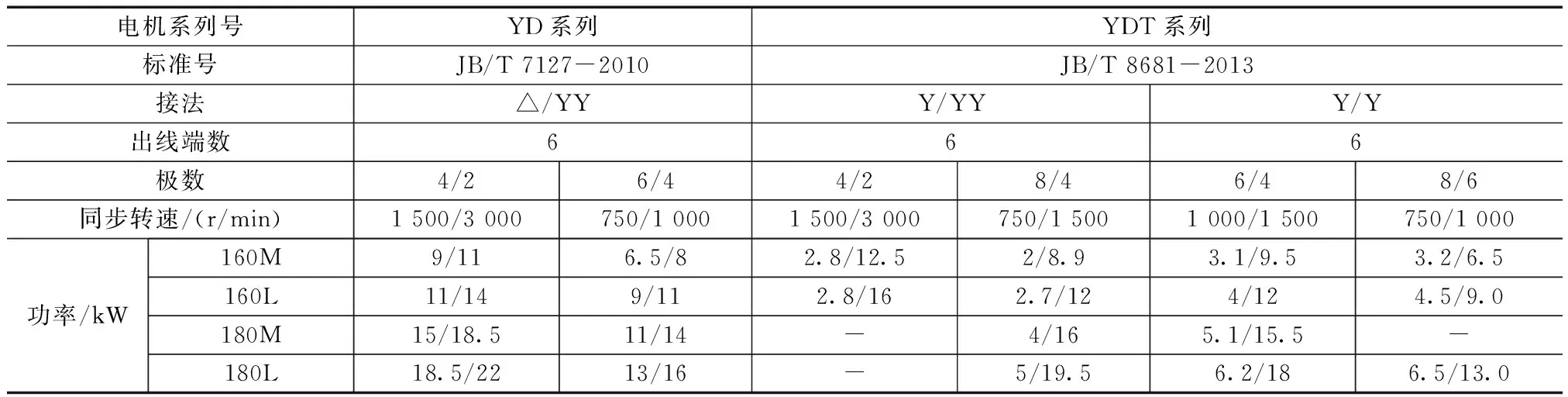
常用机座号与转速及功率的对应关系 表1

2.1 变极调速

电机的空间角度可以用“电角度”θae表达，θae=(poles/2)θa，其中poles为定子绕组形成的磁极数，θa为空间角度。电机转子机械角速度ωm与同步角速度ωs的物理关系如公式(1)～(2)所示：

ωm=(1-s)ωs

(1)

(2)

式中，s为转差率，ωe为电角速度(我国f=50，ωe=2πf=100π)。

由式(1)～(2)可知，改变磁极数即可改变同步角速度，进而实现调速。此种调速方法即为“变极调速”。变极调速的具体实现方法主要有两个：一是在定子绕组槽内嵌装一套绕组，可将一套绕组中部分线圈按一定规律反接以改变其电流方向，进而改变磁极数；二是在定子绕组槽内嵌装两套独立绕组，两套绕组的磁极数不同。

不同的绕组布放方法及引出线位置可实现不同比例的变极：倍极比变极(如表1中的4/2、8/4)、非倍极比变极(如表1中的6/4、8/6)。通过绕组的串联/并联、正接/反接、△接/Y接的组合，可实现多种极数比。图1为4/2变极的原理示意图(绕组展开图)。

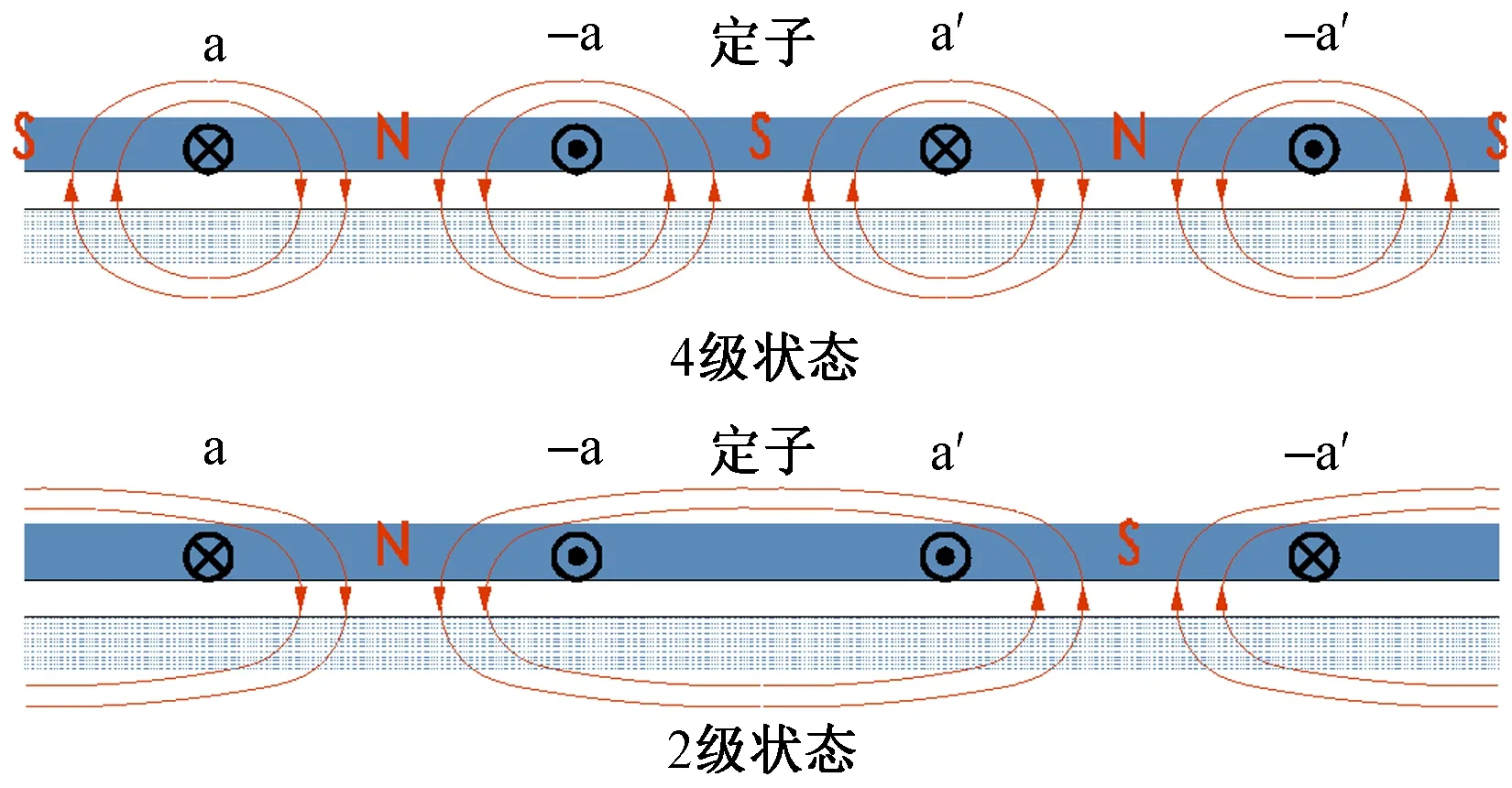
图1 变极调速原理示意图

由图1可以看出，改变a’、-a’的电流方向，磁极数由4变为2。

2.2 异步电动机的特性

电机回路经频率折算和转子绕组折算后，可获得T形等效电路，应用戴维南定理，可进一步简化为图2所示的等效电路。

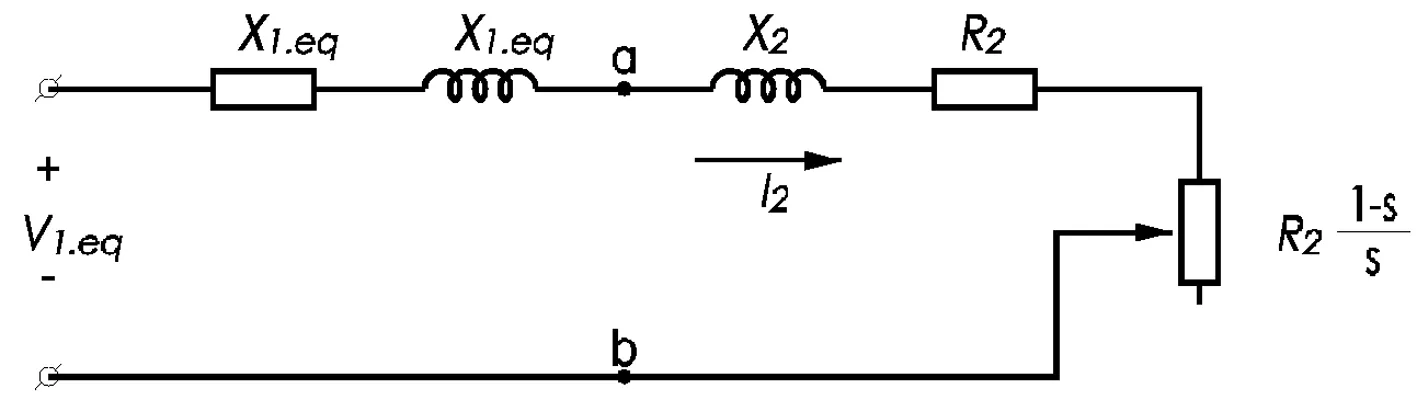
图2 电机等效电路图

根据等效电路，可得功率和转矩的计算公式如式(3)～式(5)所示：

(3)

Pem=ωsTem

(4)

Pmech=ωmTmech

(5)

式中，Pem为电磁功率，Pmech为机械功率，可以看出，在正常运行区段，机械转矩与磁极数成正比，与绕组上的电压的平方成正比，与绕组的电阻也有关系。图3所示为电机功率和转矩的关系曲线。需要注意的是，图3中设定fl为满载状态。

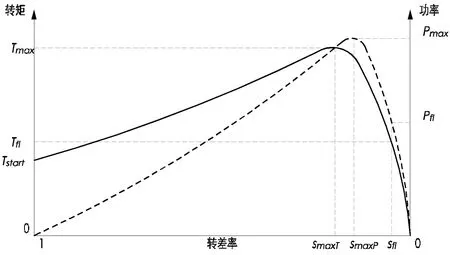
图3 电动机区域的T(s)和P(s)曲线

2.3 交流异步电动机的拖动

拖动系统的运动方程如式(6)所示：

(6)

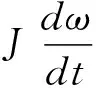
不同的负载呈现不同的特性，对于风机、泵类负载，其负载转矩为转速n的函数，二者之间的关系如公式(7)所示：

TL=f(n)=TL0+k×n2

(7)

式中，TL0为初始转矩(对风机而言，一般为0.23倍额定转矩)。

电机的选取要遵循电磁转矩Tem与负载转矩TL匹配的原则，电机过大会出现大马拉小车的现象，电机过小则无法满足设计工况。需要注意的是，电机的启动转矩Tstart应大于初始负载转矩TL0，否则无法正常启动。

3 常用变极调速的主接线及特点分析

综合上文，对常用的接线方式进行有针对性分析。△/YY、Y/YY接线较为常用，且二者主回路相同，容易混淆，故本文主要对这两种接法进行技术分析，对Y/Y接线进行简要说明。为了便于比较，△/YY、Y/YY接线均以4/2极数比进行模拟分析。

3.1 △/YY接线

△/YY的主回路见图4所示，△/YY绕组端子接线图见图5。

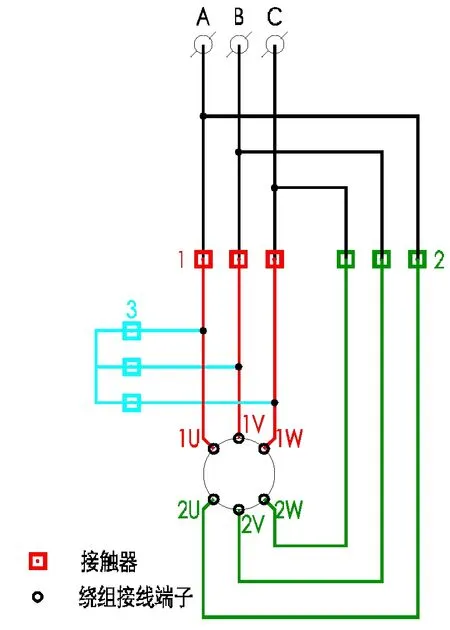
图4 △/YY、Y/YY接线主回路

图5 △/YY绕组端子接线图

需要特别注意的是，对于倍极比变极，为了使变极后电动机的转向不变，在绕组改接时，应把接到电动机端头电源的次序进行相应改变，图5中端子接线图即体现了此要求。其深层原因是电角度导致的，θae=(poles/2)θa，即电角度与极数成正比，以4/2极数比为例，若L1相的电角度为0，则2极时L2相、L3相的电角度分为120°、240°，4极时L2相、L3相的电角度分为240°、480°(等效于120°)，因而导致磁动势的旋转方向与2极时相反，若电动机端头电源的次序不变会导致两种接线下的转向不同。△/YY接线的绕组接线关系见图6所示。

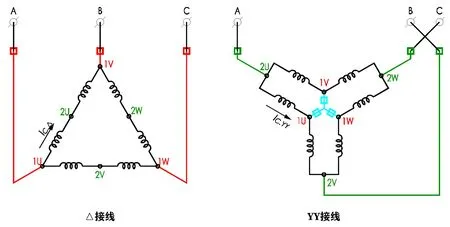
图6 △/YY绕组接线关系图

下面对比△接线、YY接线时的转矩与功率。由式(3)可以看出，机械转矩与磁极数成正比，与绕组上的电压的平方成正比。磁动势是由各段绕组建立的磁动势叠加而来的，因而分析一段绕组上的电压即可得到预期的结果：根据公式(8)～(9)可得式(10)，依据式(10)及式(5)可得式(11)。

(8)

poles△=4，polesYY=2

(9)

(10)

Pmech.△/Pmech.YY= 3/4

(11)

式中，下标“c”指图中的一段绕组。

将式(11)与表1中相应数据对比，可证明上述分析与推导的正确性。需要说明的是，表1中所列功率为输出功率，与机械功率之间差附加损耗及机械损耗，因而与式(11)为近似比例关系。

3.2 Y/YY接线

Y/YY接线的主回路与△/YY接线相同，见图4所示。对于倍极比变极，在绕组改接时，也应把接到电动机端头电源的次序进行相应改变。Y/YY接线的绕组接线关系见图7所示。

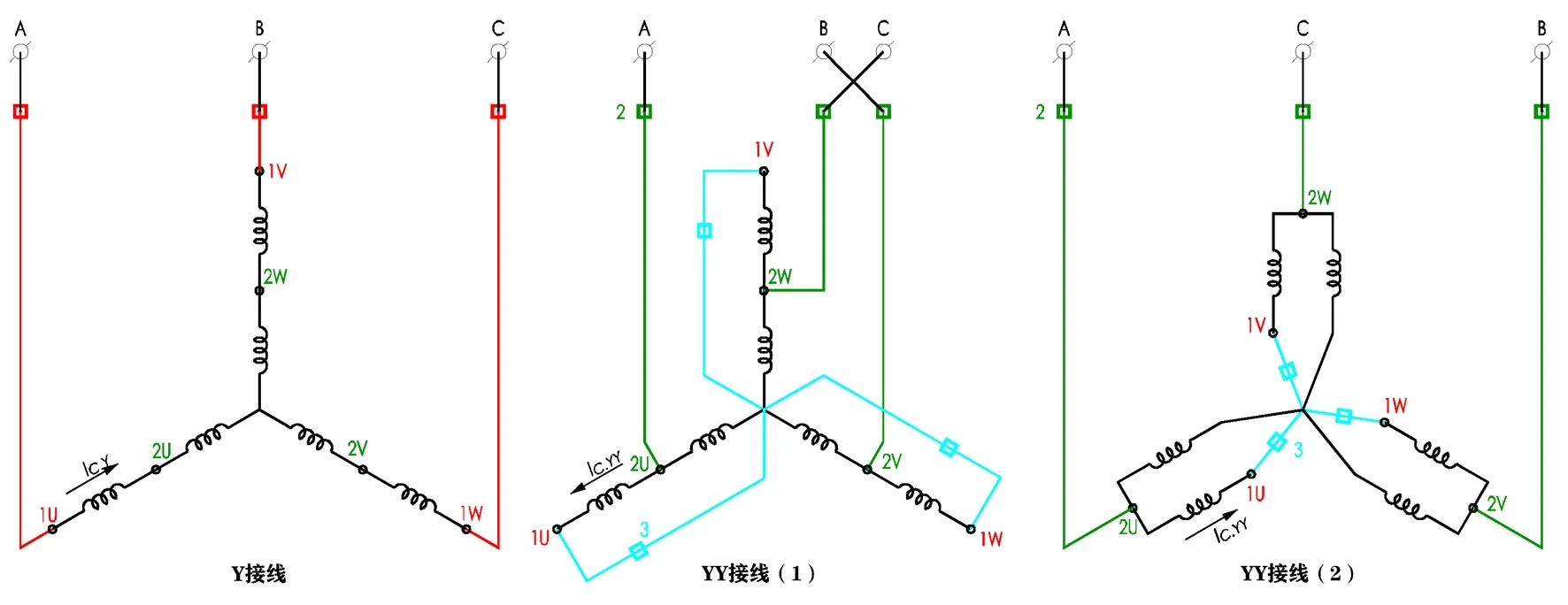
图7 Y/YY绕组接线关系图

类似于△/YY接线的分析方法，可分析出Y/YY接线的转矩与功率关系，见式(12)～(15)。

Uc.Y=1/2U0,Uc.YY=U0

(12)

poles△=4,polesYY=2

(13)

Tmech.△/Tmech.YY= 1/2

(14)

Pmech.△/Pmech.YY= 1/4

(15)

同样，将式(15)与表1中相应数据对比，可证明上述分析与推导的正确性。

3.3 Y/Y接线

Y/Y接线为2套独立绕组，绕组布放方法不同，磁极数不同；绕组自身的参数(电阻)不同，也会对转矩产生影响。由表1中可知，工程实践中，Y/Y一般被设计为功率比1/3(转速比1 000/1 500)、功率比1/2(转速比750/1 000)。Y/Y接线的主回路见图8所示。

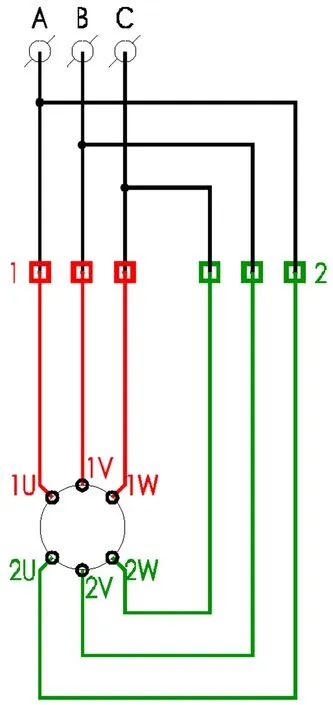
图8 Y/Y接线主回路

4 接线方式与风机负载间的匹配性分析

由前述分析可知，△/YY、Y/YY具有相同的主回路，但两种接线下具有不同的机械特性。采用△/YY接线用于风机的变极调速，需按高速运行工况设计选择风机，使机械转矩大于负载转矩(图9中实线)。但在低速状态下平衡点可见，电机性能严重浪费。而Y/YY接线与风机负载具有很好的匹配性。

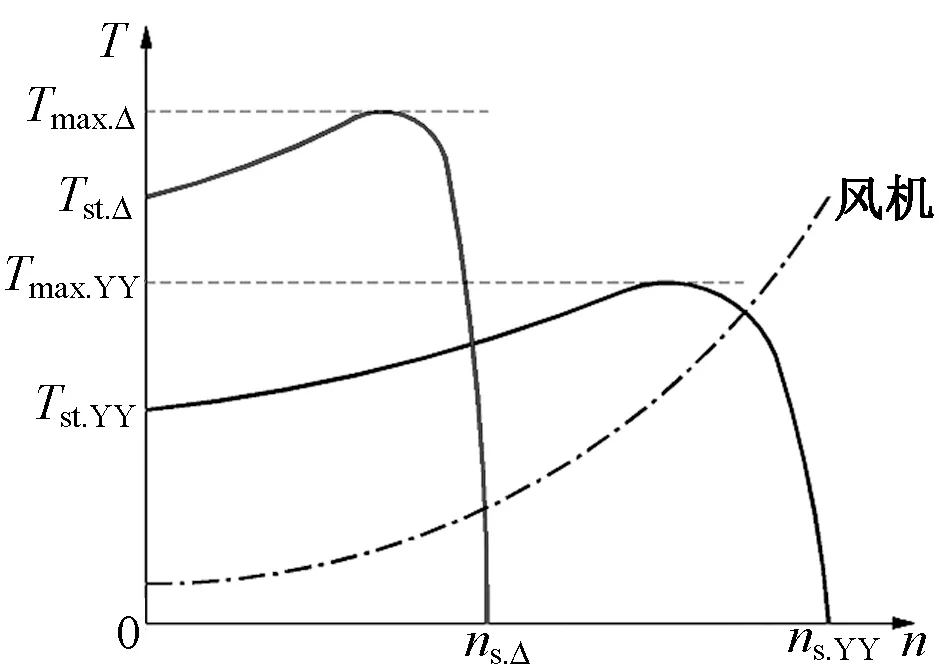
图9 △/YY接线T(n)曲线及负载TL(n)曲线

5 结束语

同为变极调速，但不同接线、不同的极数比均会导致不同的转矩比和功率比。综合对比表见表2。

△/YY接线不适合于风机类负载，更适合于恒功率负载；Y/YY接线、Y/Y接线均适合于风机类负载的变极调速。

绕组接线方式综合对比表 表2