单层服装间隙量的动态有限元模型构建与仿真

余玉坤， 孙 玥，2，3， 侯 珏,2，3， 刘 正,2,3， 易洁伦

(1. 浙江理工大学 服装学院， 浙江 杭州 310018； 2. 浙江省服装工程技术研究中心， 浙江 杭州 310018； 3. 服装数字化技术浙江省工程实验室， 浙江 杭州 310018； 4. 香港理工大学 纺织及服装学系， 香港 999077)

间隙量是指着装状态下人体与服装间的空隙部分，其对服装的舒适性、合体性、防护性能等有着重要影响，也是三维服装设计是否合理的重要评价指标。目前，学者们主要通过面料力学性能、松量分配、热湿舒适性评价等研究服装间隙量。例如：计算人体特征截面的服装间隙量,分析面料力学性能以及放松量对服装距离松量的影响[1]，建立不同角度下间隙量与放松量的回归方程[2]；利用出汗暖体假人与三维扫描仪，研究衣下间隙量对防护服热阻和湿阻的影响[3]；通过三维动作捕捉系统获取人体指定坐标，利用基于多项式近似生成的最速下降法计算服装间隙量[4]。以上传统的服装间隙量研究多采用实物测量与图形建模方法，只能获取特定部位的着装间隙量，难以获取着装整体的间隙量信息，耗时耗力。

随着CAD技术与三维虚拟现实技术的发展，利用三维模型量化表征间隙量分布逐渐成为热点[5-7]。基于图像图形技术的建模方法无法直接获得服装和人体之间的物理信息，然而，有限元数值模拟技术可通过建立人体软组织非线性材料属性、设置非线性接触边界条件，准确获取着装人体动静态下的形态压力信息。Liu等[8]通过有限元方法获得运动文胸的压力、胸部应变与织物弹性模量之间的回归方程；Sun等[9-10]模拟了人体乳房软组织的非线性特征和运动变形，利用逆问题的迭代求解方法预测了乳房超弹材料系数，基于该系数建立了准确的人体生物力学有限元(FE)模型，构建了新型个性化建模系统，用于分析穿着文胸后乳房的塑性效果和皮肤压力分布；Lin[11]和Yeung等[12]对下肢紧身裤和男性腿部结构建立了有限元接触模型，评估了腿部的接触压力。

现有基于有限元法的间隙量研究多侧重于接触压力方面，少有文献将此模型运用于服装非接触、动态间隙量的研究领域。有限元方法可模拟不同的材料属性及复杂的几何结构，建立符合人体真实结构的生物力学模型，模拟服装间隙量空间形态，获得任意部位运动状态下的间隙量信息。综上，本文构建了人体与合体服装的三维模型，通过划分人体组织网格，利用有限元仿真软件建立了着装人体有限元模型，对运动状态下间隙量进行仿真，并将仿真结果与实验测量数据进行比较验证。

1 单层服装间隙量有限元求解概述

本文的服装-人体模型为高度复杂非线性系统。Zhang等[13]建立了人体与服装接触的动态力学模型，将服装视作几何非线性的弹性壳体，人体被视作刚体。但是考虑到人体是由不同结构的弹性组织与骨骼构成的复合体，为提高有限元模型精度，本文基于Zhang等[13]的研究成果改进了模型，将服装视作几何非线性的弹性壳体，将人体认为是由不可变形的躯干部分(刚体)、可变形的胸部和周围软组织(弹性体)组成的几何体，间隙量被描述为一个并不互相穿透的动态滑动的界面。人体-服装接触坐标系如图1所示。在固定的全局坐标系(x1,x2,x3)中建立了人体与服装的相关接触系统，人体与服装被视为域Ωn,(n取1、2)：Ω1为人体域，Ω2为服装域。在时域(0,t)内，人体与服装在接触系统中的力学关系主要由运动微分方程、本构方程与边界条件 3组方程表述。

1)运动微分方程。假设t为时间，x为位置向量，u(x)为位移场，a(x)为加速度场，弹性体(服装、人体胸部和周围软组织)在t时刻的运动方程均可表示为

(1)

刚体(人体躯干部分)在t时刻的运动方程均可表示为

(2)

式中：1、2、3表示3个方向坐标轴x1、x2、x3；σji(x)为弹性体内某个点的假想平面ji上的柯西应力分量，为弹性体提供实际牵引力,N；qgi(x)为物体体力矢量i方向上的分量；ρ为物体的总密度，kg/m3，假定为常数；ai(x)为物体上质点加速度矢量i方向上的分量。

2)本构方程。假设服装与人体周围软组织为各向同性线弹性材料，因此，其本构方程由胡克定律推导得到，公式为

(3)

式中：E为弹性模量，MPa；v为泊松比；G为剪切刚度，MPa；σ1、σ2、σ3分别为弹性体内某个点在全局坐标系3个方向上的主应力，MPa；ε1、ε2、ε3分别为弹性体内某个点在全局坐标系3个方向上的线应变，%；τ1、τ2、τ3分别为弹性体内某个点在全局坐标系3个方向上的剪应力，MPa；γ1、γ2、γ3为弹性体内某个点在全局坐标系3个方向上的剪应变，%。

由于人体胸部组织的特殊性，其在变形较大的情况下会呈现非线性材料特性，因此，对于此类材料，需要用非线性超弹材料模型来定义。其本构关系可用应变能密度来描述，公式为

(4)

式中：w1为体力对弹性体作的功，J；w2为面力对弹性体作的功，J；Cw1w2为利用w1、w2表征乳房材料非线性弹性行为的超弹性参数，MPa；I1、I2为柯西-格林变形张量B分量的第1、2个不变量。I1、I2的具体形式为

(5)

式中：tr(B)为矩阵B的轨迹；矩阵B为变形轨迹矩阵F与其转置矩阵FT的乘积。

3)边界条件和初始条件。系统的边界条件包括重力和服装人体间的接触力，其中重力表示为

(6)

(7)

(8)

人体与服装运动的初始条件包括3个部分：以速度Vx在x1方向上的运动；以速度Vy在x2方向上的运动；以速度Vz在x3方向上的运动，公式为

(9)

式中，V1(x)、V2(x)、V3(x)分别为人体与服装上某个点在全局坐标系3个方向上的速度，m/s。

2 人体-服装动态有限元建模与仿真

2.1 人体-服装三维模型建立

本文招募了符合165/84A体型(GB/T 1335.2—2008《服装号型 女子》)的标准女性受试者，身高为165 cm，体重为110 kg，胸围为82 cm。通过美国[TC]2非接触式三维人体扫描仪获得人体点云数据，利用逆向建模软件将模型分割为3个部分：人体躯干部分、外部软组织层(厚度为 2.3 cm[14]， 以下简称外部软组织)和柔软的乳房，使用平滑与填孔功能保证模型表面光滑，获得人体躯干的实体模型。采用计算机辅助工程(CAE)平台，对实体模型各部分进行5 mm四面体网格的划分，得到符合人体基本结构的有限元人体模型。

本文实验款式选取合体女性背心，号型为164/84A，胸围松量为8 cm，腰围松量为8 cm。在逆向建模软件中绘制胸围线、腰围线、前中、后中及相应的辅助线，结合人体模型提取的特征轮廓线建立服装曲面，采用5 mm三角形网格对服装模型进行划分，得到服装的有限元模型。建模流程如图2所示。

2.2 有限元模型材料参数获取

人体有限元模型各部分(躯干部分、外部软组织和乳房)被赋予不同的材料属性。为简化模型，本文假设各部分材料类型均为各向同性。乳房被定义为非线性超弹性材料，选取了2组Mooney-Rivlin材料模型[9]对乳房进行预实验，根据式(4)材料模型Rivlin系数分别为C10、C01、C11、C20、C02。其2组系数参数分别为0.25、0.26、1.87、3.90、3.40 kPa与0.05、0.05、0.38、0.78、0.68 kPa。模拟结果表明,第1组数据仿真结果与真实情况拟合度较高，第2组数据获得的乳房模型较为僵硬，与真实情况拟合度存在10 cm左右误差，因此，本文选用第1组数据作为乳房材料参数。外部软组织力学参数参考文献[15-16]。实验样衣面料为纯棉平纹机织布，参照FZ/T 70006—2004《针织物拉伸弹性回复率试验方法》，利用Instron 3344万能拉伸仪(美国Instron公司)测试其力学性能。在大气温度为(20±2) ℃、相对湿度为(65.0±3.0)%的环境下静置24 h后进行测试。有限元模型材料的具体参数如表1所示。

2.3 人体-服装运动坐标获取

本文使用瑞典Qualisys三维动作捕捉系统获取人体-服装的坐标。

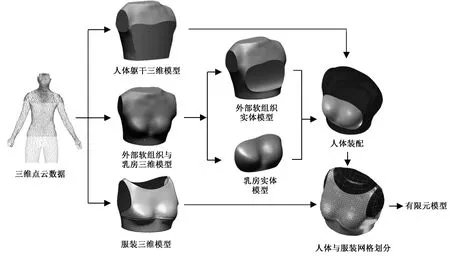
图2 人体-服装三维模型建模流程Fig.2 Modeling process of human body garment 3-D model

表1 有限元模型材料参数Tab.1 Material parameters of finite element model

为获取服装与人体胸围1周的运动坐标，本文进行了2组测试实验，如图3所示。

图3 三维动作捕捉仪测试示意图Fig.3 Test diagram of 3-D motion capture instrument.(a) Sticky marking ball; (b) Sticky marking ball of computer-perspective

在后颈点、左右肩点、左右锁骨点(以下统称为骨骼点)各设置 1个标记球，用于捕捉躯干部分的运动轨迹。第1组实验将25个直径为12.5 mm的反光标记球均匀黏贴于服装胸围截面与骨骼点；然后受试者以6 km/h的速度在跑步机上运动，进行3次实验获得服装胸围标记球的空间坐标。第2组实验将同样25个反光标记球均匀黏贴于人体胸围截面与骨骼点，然后以6 km/h的速度在跑步机上运动，进行3次实验获得人体胸围标记球的空间坐标。在2组实验中分别选取躯干运动标记点误差最小的1组数据，确保计算得到的动态间隙量的准确性。将实验获取的间隙量与有限元数值模拟结果做对比，用于验证有限元仿真间隙量的精确度。

2.4 人体-服装有限元模型构建

人体与服装模型构建完成后分别导入有限元软件，按照穿着状态进行服装与人体模型的装配，获得完整的有限元模型如图4所示。为说明不同结构单元之间的关系，本文通过接触表来解释单元间的接触关系。服装覆盖外部软组织与乳房，运动时二者之间产生滑移，接触定义为变形体与变形体的接触(T)； 外部软组织、乳房与身体内部刚体相黏连，运动时不产生滑动，此时接触定义为变形体与刚体的黏结(G)，具体如表2所示。

2.5 边界条件定义

根据重力及其分量(式(5)和(6))，设置人体与服装重力边界条件，可视化结果如图5(a)、(b)所示。根据动作捕捉人体躯干三维坐标运动数据，参照式(7)计算，赋予有限元软件中的刚体作为位移边界条件(见图5(c))驱动整个人体模型，模拟骨骼驱动的人体着装运动形态。

图4 人体与服装有限元模型Fig.4 Finite element model of human body(a) and clothing(b)

表2 人体与服装接触类型表Tab.2 Human body and clothing contact types

图6 不同时间下着装状态的位移云图Fig.6 Cloud picture of displacement in state of dressing at different times

图5 有限元模拟中的边界条件Fig.5 Boundary conditions in finite element simulation.(a) Gravity boundary conditions of human body;(b) Gravity boundary conditions of clothing;(c) Displacement boundary conditions of human torso

3 结果与分析

3.1 有限元仿真结果

通过有限元建模软件计算，得到运动状态下着装模型的位移云图如图6所示。可以看出：位移最大的为腰部，数值达19.918 mm；肩部位移最小，数值为 17.770 mm。 这体现了以6 km/h步行时，由于重力作用，肩部服装与人体接触面积较大，运动时产生贴合人体的滑移，因此，位移不明显，而腰部服装与人体接触面积最小，运动时位移幅度较大。

图7示出净体运动1个周期内的位移云图。可看出：身体外部软组织的位移依据运动状况呈现相应变化；乳房位移变化最大，达到381.4 mm，这可解释为以6 km/h步行时，外部软组织密度与硬度较大，而本文中乳房被视作超弹性材料，密度与硬度相对于外部软组织较小，所以受到相同的力作用时，位移变化较大；腰部位移变化最小，为381.2 mm，这是由于腰部软组织较少，运动时受到的影响也较小，因此，位移变化最小。

图7 不同时间时净体的位移云图Fig.7 Net body displacement cloud picture at different times

3.2 着装间隙量仿真结果

本文采用人体横截面表面点到服装的法线距离来定义腰截面处着装间隙量[18]，以人体胸围截面中心作为坐标原点，每隔30°作射线对胸围截面进行区域划分，计算射线位置的间隙量值。

为更清晰地分析间隙量仿真结果，提取同一周期内服装与净体胸围截面位移的坐标数据，在CAD软件中进行坐标的曲线拟合，分别计算周期内6个时间点(T1～T6，其中：T1为周期起始时间点；T2为周期起始时刻与位移最大时刻的中间时间点；T3为周期内位移最大时间点；T4为位移最大时刻与位于最小时刻的中间时间点；T5为位移最小时间点；T6为周期结束时间点)不同区域的间隙量数值，如图8所示。

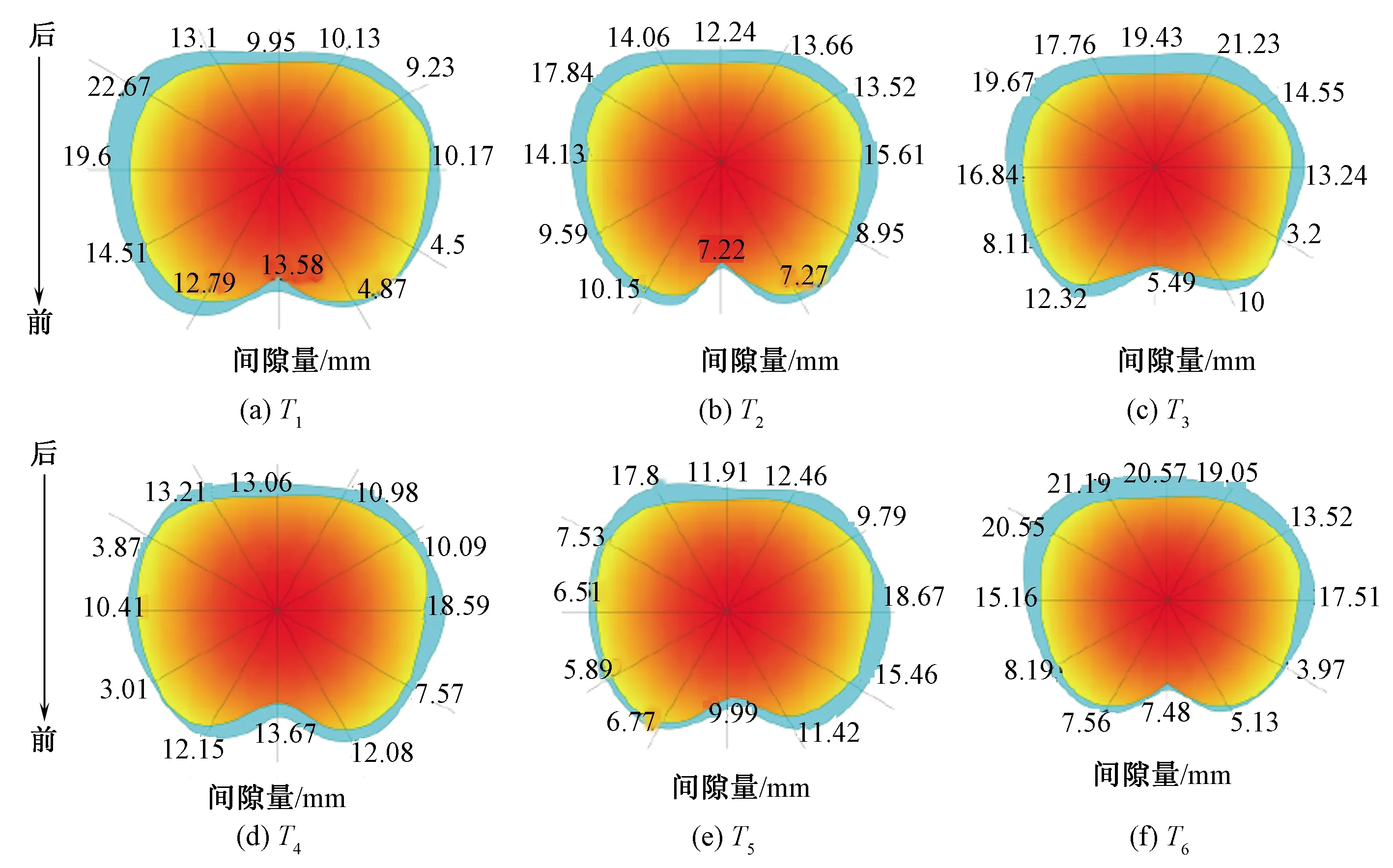
图8 不同时间点间隙量仿真数值Fig.8 Gap simulation value at different times

由图8可看出，在6 km/h运动速度下，胸围间隙量在人体后侧变化较大：最大值在右侧肩胛骨处，达22.67 mm；最小值在右胸侧,为3.2 mm。在运动过程中人体后侧间隙量均值为14.487 mm，变化较大。这可理解为人体直立运动时，肩胛骨对服装有支撑作用，后侧服装与人体接触面积小，因此，间隙量较大。而乳房周围的间隙量变化较小，均值为 8.763 mm， 这是由于在重力作用下服装与胸部较为贴合，在运动时有了胸突(BP)点的支撑，使得胸部服装的间隙量变化较小。

上述结果表明，通过定义人体不同组织结构，赋予不同材料参数的方法，可使模型仿真更贴近真实人体运动状态，采用内部刚体带动外部软组织最终引起间隙量变化的方法，可较为理想地模拟运动状态下胸围间隙量。

3.3 有限元仿真结果验证

根据2.3节实验测量并计算获得间隙量结果，与有限元仿真结果进行对比分析，验证有限元模型仿真结果的可靠性，结果如图9、10所示。分别选取人体前中、后中、左BP点、右BP点的仿真模拟数据与实际数值进行对比。数据分析表明，人体前中、后中与左右BP点的仿真运动趋势与真实运动趋势基本一致。

图9 人体胸围截面主要部位运动趋势验证Fig.9 Movement trend verification of main pares of human bust section. (a) Movement trend of front center; (b) Movement trend of left BP point; (c) Movement trend of right BP point; (d) Movement trend of back center

图10 服装胸围截面主要部位运动趋势验证Fig.10 Movement trend verification of main parts of clothing bust section. (a) Movement trend of front center; (b) Movement trend of left BP point; (c) Movement trend of right BP point;(c) Movement trend of back center

为获取整个运动周期的误差，本文采用平均差和均方根误差表征仿真与测量实验结果的差值。人体前中、左BP点、右BP点、后中的平均差分别为0.44、8.35、0.24、19.4 mm，均方根误差分别为1.88、8.61、1.81、20.5。其中右BP点与前中的平均差值与均方根误差较小。后中点误差最大的原因可能是实际运动中，肩胛骨与人体转动对间隙量的影响较大，而本文为简化模型，提高计算效率，忽略了肩胛骨对服装的支撑与人体转动因素，因此，后中点的误差最大。虽然有大量文献将人体作为同质且密度分布均匀的弹性体进行有限元分析，但是不同的人体组织结构在运动中的形变仍有很大的未知性，而将人体视为统一的弹性体难以模拟不同区域真实的形变，模拟结果与真实结果的相关性在0.2～0.8之间[18-20]，其中服装压力模型的拟合优度较高，因为压力只与人体表面组织的材料参数有关。本文实验结果说明将人体不同区域赋予不同材料参数建立的有限元仿真模型，可较为准确地模拟人体前后、左右乳房的真实运动情况。

本文通过计算得到服装前中、后中与左右BP点的仿真运动趋势，与三维动作捕捉系统获得的实际运动趋势基本吻合，前中、左BP点、右BP点、后中的平均差分别为2.55、6.71、6.95、6.51 mm，均方根误差分别为3.23、8.12、8.10、7.74，服装前中点平均差值与均方根误差最小。许多研究者采用实验和数值方法对间隙量进行研究[21-23]，评价运动状态下间隙量的分布及表征，难以获得着装空间完整的形态信息，且实验结果可重复性较差。基于有限元方法的间隙量动态仿真模型可在合理范围内有效地模拟真实运动状态下的服装形态变化，并能够一次性提取模型任意部位的坐标值，快速获得服装间隙量。

为更加直观准确地描述仿真结果的真实性，将三维动作捕捉实验的间隙量数值与有限元模型间隙量仿真结果进行比较，T1～T6时间节点胸围间隙量的平均差值分别为2.78、2.83、4.88、2.54、3.77、2.84 mm，整体上间隙量差值均小于5 mm。为进一步验证动态间隙量变化的趋势，计算了2组间隙量数据在运动1个周期内，T1～T66个即时节点人体各个区域的间隙量相关性(α=0.1)，结果如表3所示。

表3 间隙量相关性分析Tab.3 Correlation analysis of clearance

由表3可知，人体以6 km/h的速度运动时，间隙量真实值和仿真值在置信区间为90%的条件下，具有显著相关性，说明本文提出的间隙量动态模拟方法具有较好的可信度。

4 结 论

1)本文根据人体不同组织结构的特性，提出了具有针对性的人体-服装动态有限元建模方法：将人体三维模型分为躯干、软组织与乳房3个部分，并分别定义不同的材料参数；将三维动作捕捉系统测得的躯干运动坐标数据赋予内部刚体，由内部刚体运动带动软组织与乳房，进而形成服装间隙量。构建的人体-服装有限元模型符合人体生理结构，仿真间隙量的生成方式也符合实际间隙量定义，为基于有限元模型构建的动态间隙量仿真方法研究提供了新思路。

2)本文通过对有限元软件动态间隙量的模拟仿真进行研究，建立了基于单层合体松量服装的动态有限元模型。将仿真结果与三维动作捕捉实验结果对比，验证间隙量数据。结果表明，模拟数据与真实数据最小平均差值为0.24 mm，最小均方根误差为1.81，对同1个运动周期6个时间节点下 2组数据相关性进行分析，在置信区间为90%的条件下具有显著相关性。

3)在实际应用中，可根据不同面料参数对单层服装动态间隙量进行仿真，进而指导服装版型的优化，以及为基于不同面料服装间隙量的仿真研究提供开发思路。

致谢香港理大学人工智能设计实验室。