稀疏角度数据下非视域物体三维重建方法研究

王雪峰,张自豪,陈兴稣,王元庆

(1.伊犁师范大学网络安全与信息技术学院,新疆 伊宁 835000；2.河南工业大学人工智能与大数据学院,河南 郑州 450001;3.南京大学电子科学与工程学院,江苏 南京 210093)

1 引 言

非视域成像技术是近年来的研究热点技术,是刚发展起来的一种间接成像技术,在医疗成像、灾难救援、军事反恐及城市街道安全侦查等都具有重要的研究意义。非视域成像技术通过激光照射中介面,主要是通过光在中介面进行多次反射和散射来获取隐藏物体的信息,再使用一定的重建算法对采集的数据进行处理,才能完成非视域物体的三维重建。美国麻省理工学院的Velten等人[1-2]利用飞秒激光和条纹相机进行拐角成像,首先使用反投影重建法,实现了非视域物体的三维重建。为了提高重建的精度,对反投影法的优化算法被相继提出,如使用时间选通门技术及单光子相机来对隐藏物体进行逐层探测[3-5],使用快速反投影算法来提高重建的速度[6],利用椭圆投影特点进行椭圆模型消除重建的伪影[7],文献[8]提出了两个权重因子应用在滤波反投影算法中,减少了条纹效应,并能有效应用到噪声数据中。采用f-k偏移方法[9]为镜面反射对象产生更高质量的重建；O′Toole等人[10-11]使用光锥变换及共聚焦光路对隐藏物体进行探测；Xin等人[12]使用费马流算法得到了较高的重建精度。

由于反投影法需要采集足够的数据(全部角度范围),才能较好的完成三维重建,所以需要光源进行扫描式数据采集,需要大量时间,但是在实际的应用中,特别是对于较危险的物体,如反恐及灾害救援,需要快速、有效的进行数据采集,并能够快速完成三维重建,这就对非视域成像技术及重建算法提出了新的挑战。本文针对稀疏角度数据问题,提出了反投影修正MLEM(最大似然期望值最大化)算法,能够有效提高非视域物体三维重建的精度。

2 基于APD阵列的非视域成像

现有大多数成像方式为反射式成像,也称为拐角成像,本文采用透射式成像方式,成像设置的示意图如图1所示,激光照射中介面一点(如图中D点),光透射中介面后,中介面选择扩散膜(不能透过扩散膜直接观测到后面的物体),继续散射到扩散膜后面的隐藏物体,光会再次被隐藏物体进行散射和反射,并返回到扩散膜后被探测器APD接收,其中图1中参考光是检测光源的出光时间,作为探测器APD接收信号的时间基准。本文提出的基于APD阵列的透射式非视域激光成像系统具有成像结构简单、操作方便且无需场景扫描、能够快速完成数据采集的特点。探测器布置在扩散膜附近,直接探测隐藏目标散射回来的光信息。一次激光照射后,APD阵列接收来自隐藏目标多个方向的信息,这相当于进行了多点信息接收,因此不需要进行场景扫描,使数据采集一次完成。

图1 本文提出的透射式非视域激光成像示意图

探测器阵列的排布方式采用矩形阵列方式,如图2所示,以3×3的阵列为例,不同的探测器阵列(如圆环形状和十字形状等)采集到的数据会有不同,获取的隐藏目标的信息也会有所不同,对于重建算法有一定的影响。本文中使用的探测器单元由4个APD单元组成,详细的APD单元排布方式如图1所示。4个APD排布在扩散膜的四个对角位置,排布成2行2列的矩阵阵列的方式,四个APD分别标记为APD11、APD12、APD21和APD22。矩形阵列探测的数据表示为:

本文提出的透射式非视域成像的光传输过程如图3所示。

图2 矩形阵列的探测器排布方式

图3(a)中,首先激光照射扩散膜D点,光经过扩散膜后,继续传输到隐藏物体上(如点S1、S2和S3),传输路径为D→S1、D→S2和D→S3,传输距离为rd1、rd2和rd3；其次光经过隐藏物体后再次传输到扩散膜,并被探测器APD接收,如其中一个APD探测单元在A点,则传输路径为S1→A、S2→A和S3→A,传输距离为rs1、rs2和rs3；最后在A点的APD探测器单元接收信号的路径为D→S1→A、D→S2→A和D→S3→A,传输距离为rd1+rs1、rd2+rs2和rd3+rs3,则接收信号的三个时间点(ts1、ts2和ts3)如图3(b)上面所示,对应图3(a)中隐藏物体的三个点(S1、S2和S3),则ts1=(rd1+rs1)/c、ts2=(rd2+rs2)/c和ts3=(rd3+rs3)/c,其中c为光速。

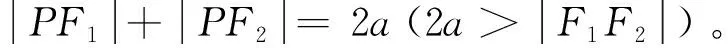
图4 非视域成像的椭圆投影原理图

图4中两个定点是光源D点和探测器A点,隐藏物体上的点即是某个椭圆上的点,如椭圆f1上的动点p3；隐藏物体上的两点p1和p2在同一个椭圆f2上,则p1和p2会在同一个时间点返回信息到探测器上,即光经过D点后传输到隐藏物体上两点p1和p2,并投影到探测器上,这就是非视域成像中的椭圆投影方式。后期的图像重建也是根据反投影方法的原理,首先将隐藏物体划分为三维像素块(称为体素,如图4中p1、p2和p3),然后根据椭圆反投影方法对隐藏物体的每个体素进行重建,最终完成整个物体的三维重建。

3 基于BP-MLEM的非视域物体重建算法

3.1 MLEM算法

MLEM算法是最大似然期望值最大化算法(maximum likelihood expectation maximization),它使用期望最大化EM(expectation maximization)算法[13-14]来完成最大似然的估计,是一种统计迭代算法,以“参数估计理论”为基础,基于观测数据统计模型的重建算法,广泛应用于CT及PETCT图像重建[15-16],CT图像重建的主要思想也是反投影[17],所以也需要完整的数据才能完成较好的重建,但实际中无法完成180°范围的数据采集,且需要采集的时间间隔要小、均匀才能更好的重建图像,针对CT图像重建中稀疏角度数据的问题,可以使用迭代重建算法。

MLEM算法是根据最大似然估计理论,假设认为每次椭圆投影符合泊松分布,根据似然函数,求投影数据的最大概率,推导得出计算公式,而此公式正好为非线性方程,很难给出解析解,只能通过迭代的方法来求近似解,通常采用期望最大化(EM)来求解。由此,推导得出了MLEM算法,迭代公式[18]如下:

(1)

其中,重建体素设为xj;重建体素个数为M个;投影矩阵中椭圆个数为i个;投影矩阵元素aij表示第j个体素xj对第i个椭圆的贡献值;pi表示第i个椭圆的投影值。

基于APD阵列的非视域成像MLEM算法的具体步骤如下:

(4)计算第j个重建体素xj的修正值:

(2)

(5)对重建体素xj的值进行修正:

(3)

这里用穿过该体素的所有椭圆对它进行修正,即完成一轮迭代。

(6)k=k+1；将以上迭代的结果作为初值,重复步骤(2)到(5)进行新一轮迭代,直到取得符合收敛条件为止。

3.2 BP-MLEM算法

针对非视域成像的特点,仅能在稀疏角度下获取数据,提出了BP-MLEM(Back Projection -MLEM)迭代重建算法,更加适用于非视域成像,改进的方法对伪影和噪声的抑制较好,且具有更快的收敛速度。

MLEM算法中比较重要的迭代过程是修正方法,它决定了每次迭代结果后的修正方向,为了更快更准确的得到收敛结果,需要迭代方向每次都往正确的结果修正,这就需要更好的修正方法,MLEM算法修正方法的修正值为:

采用上次迭代结果和修正值进行相乘的方法进行迭代,即下一次迭代值是上一次迭代值与反投影乘积的结果。这样迭代后图像中较大的值增长越大,较小的值增长较慢,图像的对比度越来越大,即迭代速度快,但有时速度过快,容易造成过收敛,不能得到理想的收敛结果。

本文提出的基于反投影迭代BP-MLEM算法,迭代公式如下:

(4)

其中,重建体素设为xj;重建体素个数为M个;投影矩阵中椭圆个数为i个;投影矩阵元素aij表示第j个体素xj对第i个椭圆的贡献值;pi表示第i个椭圆的投影值。

基于APD阵列的非视域成像BP-MLEM算法的具体步骤如下:

(4)计算第j个重建体素xj的修正值为:

(5)

(5)对重建体素xj值进行修正,方法为:

(6)

这里用穿过该体素的所有椭圆对重建体素xj进行修正,并将反投影BPΔi加入到修正方法中,这样就完成一轮迭代。

(6)k=k+1；将以上迭代的结果作为初值,重复步骤(2)到(5)进行新一轮迭代,直到取得符合收敛条件为止。

4 实验结果

实验设置如图1所示,隐藏目标选择“十”字形状,距离探测器220 cm,4个APD探测器的位置如图1所示。分别使用反投影算法、MLEM算法和BP-MLEM算法进行实验,为了更好的进行对比实验,本文进行了多次迭代重建,分别给出不同迭代次数的对比结果。

图5显示了使用传统的反投影算法得到重建结果,反投影算法中使用了R-S-L滤波算子,从图中可以看出,反投影的重建结果存在较大的伪影,重建结果精度不高。

图5 滤波反投影算法重建结果图

图6显示的是使用MLEM算法对非视域物体“十”字的重建结果,分别显示了4次不同迭代次数(分别是第3、4、9、20次迭代),从图中可以看出,当第3次迭代(图6(a))时,重建结果图的伪影在减少,但是重建结果图并不理想,图像中心点强度很高,而边缘强度很低(接近背景色),不能较好的重建“十”字形状的结果；再次进行6次迭代后,即第9次迭代(图6(c)),重建结果的伪影比第3次迭代少,但是重建的结果仍然是中心点强度过大,而边缘强度太小；当达到第20次迭代时,重建结果反而没有最初的迭代结果好,几乎无法重建“十”形状结果,这就是MLEM算法迭代速度过快,从而产生过收敛的结果。

本文提出的BP-MLEM算法的重建结果如图7所示,同时也给出了4个不同迭代次数(分别是第3、4、9、20次迭代),总体来看,4次迭代的重建结果都能够重建出“十”字形状图,并且随着迭代次数的增加,重建伪影在不断减少,重建的精度也在不断增加；当迭代次数达到4次时(图7(b)),物体“十”字形状就得到了较好的重建结果图；当迭代次数不断增加时,重建结果没有出现MLEM算法的过收敛结果,而是达到了更好的重建效果,重建结果图像趋于稳定。实验表明,BP-MLEM算法能够在较少的迭代次数下,得到较好的重建结果；并且当迭代次数增加时,重建算法能够得到较稳定的重建结果图,不会出现过收敛等问题。

为了更加准确的对比实验结果,本文使用了SSIM(Structural SIMilarity)结构相似度来评价重建结果图的图像质量,对比实验结果显示在图8中,分别对使用BP-MLEM算法的重建结果图(图7)和MLEM算法的重建结果图(图6)计算SSIM值,图8中分别计算了第3、4、9、20次迭代的SSIM值,其中第一个值(横坐标标识为BP)是使用反投影算法重建结果图(图5)。从图8中可以看出,利用BP-MLEM算法重建结果图的SSIM值都高于MLEM算法重结果图的SSIM值,而且随着迭代次数的增加,BP-MLEM算法的重建结果图的SSIM也在不断增加,表明重建结果图的质量在不断增加；而MLEM算法的重建结果图的SSIM值虽然刚开始也在不断增加,但增加的趋势较慢,且当迭代次数为第9次和20次时,SSIM值基本没有增加,表明重建结果图的质量并没有随着迭代次数的增加而不断增加。

图8 BP-MLEM算法与MLEM算法重建结果图在 不同迭代次数下的SSIM值对比图

5 结 语

图像重建算法在非视域成像系统中具有重要的作用,它关乎着整个系统的实现结果,对实验系统的验证起到了关键作用。本文构建了基于APD阵列的透射式成像系统,快速进行隐藏物体探测,一次完成数据采集,不需要使用光源进行扫描成像；并针对非视域成像系统仅能在稀疏角度下获取不完整数据的特点,提出了BP-MLEM迭代算法,实验结果表明,相比反投影算法,能够更好的去除伪影；并且能在较少的迭代次数下,得到较好的重建结果图；当重建次数不断增加时,重建结果趋于稳定,表明BP-MLEM算法较稳定,不会出现过收敛等问题。