排序集抽样下随机截尾数据的平均寿命估计

张良勇，董晓芳

(河北经贸大学 数学与统计学学院，河北 石家庄 050061)

排序集抽样(ranked set sampling，RSS)方法是在估计澳大利亚农场牧草产量时首次被提出的，已被广泛应用到系统可靠性、质量管理、临床医学、生态环境等领域[1-6].排序集样本不仅包含了样本信息，还包含了次序信息.在实际中只要感兴趣的样本不易具体测量，但较容易直观排序时，RSS方法比简单随机抽样(simple random sampling，SRS)方法更加有效.例如，Awais等[5]将RSS方法应用到产品质量控制图方面，并证实了其抽样效率明显高于SRS方法.Risch等[6]采用极值RSS方法对配对亲属进行遗传相关性试验，论证了试验效率能得到显著地提高.

随着RSS方法的广泛应用，基于RSS的统计问题被研究，并获得许多重要的成果.以下只列举RSS下总体均值的非参数估计代表性研究成果.Dell等[7]利用排序集样本均值估计总体均值，并证明了此估计量具有无偏性和适应任意分布性.Ozturk[8]研究了总体均值的RSS极大似然估计.Bocci等[9]通过对意大利第5次农业调查的实例分析，验证了RSS方法在估计总体均值上的高效率.Balci等[10]给出了RSS下总体均值的修正极大似然估计量.Wang等[11]研究了临床医学中聚类随机设计总体均值的RSS估计问题.李涛等[12]研究了无重叠k-序对RSS下总体均值的估计问题.

文献[7-12]均通过估计效率的比较，证明了RSS方法的抽样效率高于SRS方法.但是，这些文献研究的RSS测量值都是完全数据.然而在许多寿命试验中，由于种种条件的限制只能得到随机截尾数据，其统计分析在可靠性工程、医药卫生、环境科学等领域都有广泛的应用[13-14]，因而研究RSS下随机截尾数据的统计推断就变得非常重要.平均寿命是刻画产品寿命的重要度量指标，它在寿命分析中的地位相当于完全观测下的总体均值.为了提高估计效率，本文利用RSS下随机截尾数据，采用平均秩思想，构建总体平均寿命的非参数估计量，分析新估计量的性质，并与SRS下相应估计量进行估计效率的比较.

1 排序集抽样过程及其样本特点

RSS方法的具体抽样过程：第1步，从总体中随机抽取m2个个体，随机分为m组，每组m个；第2步，利用主观经验判断、专家观点等易于获得的直观感知信息对每组进行由小到大的排序； 第3步，在第i个小组中抽出次序为i的个体，i=1,2,…,m.

以上过程称为一次循环，为了增大样本量，循环重复k次.若令T(i)j表示在第j次循环中从第i组中抽出次序为i的样本单元，则排序集样本表示为

最终只对这n=mk个样本单元进行实际测量.排序集样本的显著特点有：1)排序集样本单元之间相互独立；2)每一行的样本单元之间独立同分布；3)每一列都包含了各个秩次的信息.为简便，排序集样本一般记为T(i)j，i=1,2,…,m;j=1,2,…，k.

2 平均寿命的RSS非参数估计量

令非负随机变量T表示产品的寿命，R(t)=P(T>t)表示T的可靠度函数.当T的分布未知时，想要估计T的平均寿命μ，定义为

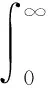
(1)

令T(i)j,i=1,2,…,m;j=1,2,…,k为抽自T的排序集样本；Cij(i=1,2,…,m；j=1,2,…,k)表示截尾的随机变量，非负独立同分布，具有分布函数G.在随机截尾模型下，只能观察到

Y(i)j=min(T(i)j，Cij)，δ(i)j=I(T(i)j≤Cij),i=1,2,…,m；j=1,2,…,k.

对于任意的i(1≤i≤m)和j(1≤j≤k)，Y(i)j的分布与j无关，其分布函数为

H(i)(t)=P(Y(i)j≤t)=1-P(Y(i)j>t)=1-P(T(i)j>t,Cij>t)=1-R(i)(t)[1-G(t)]，

其中,R(i)(t)为样本量为m的SRS第i次序统计量的可靠度函数.

从排序集抽样过程可知，Y(i)1,Y(i)2,…,Y(i)k可以看作可靠度函数为R(i)(t)和平均寿命为μ(i)的随机截尾模型下SRS样本，其中μ(i)为样本量为m的SRS第i次序统计量的平均寿命.这样，可以利用Gill[15]的研究方法来构建μ(i)的非参数估计量.

令Y(i:1:k)≤Y(i:2:k)≤…≤Y(i:k:k)是Y(i)1,Y(i)2,…,Y(i)k的次序值，μ(i)的非参数估计量定义为

(2)

其中,δ(i:r:k)是Y(i:r:k)的δ值.

根据式(2)，采用平均秩思想，总体平均寿命μ的RSS非参数估计量定义为

(3)

3 新估计量的渐近正态性

下面证明一个重要的定理.

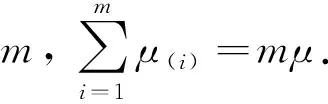
证明： 由文献[16]知，对于任意给定的m，

于是

定理得证.

定理2若R和G连续，且满足

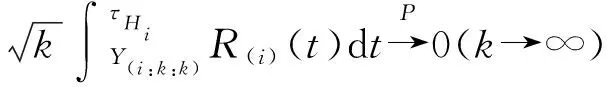
其中

证明：由式(3)、定理1和n=mk，得

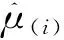
其中

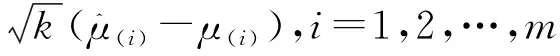
4 估计效率

令T1、T2、…、Tn为抽自总体T的简单随机样本，C1、C2、…、Cn表示截尾的随机变量，非负独立同分布，具有分布函数G.在随机截尾模型下，只能观察到Yi=min(Xi，Ci)，δi=I(Ti≤Ci),i=1,2,…,n.设Y(1)≤Y(2)≤…≤Y(n)是Y1,Y2,…,Yn的次序值，δ(i)是对应于Y(i)的δ值.Gill[15]定义了μ的SRS非参数估计量

(4)

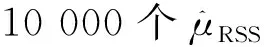
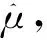
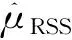
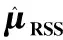
表1 平均寿命估计量与的相对效率

5 应用

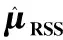
表2 铝条寿命中与的均方误差

6 结论

本文利用RSS下随机截尾数据，建立了总体平均寿命的非参数估计量，证明了新估计量的渐近正态性，给出了新估计量的渐近方差，模拟比较了新估计量与SRS下相应估计量的估计效率，并进行了实际应用分析，研究结果表明：RSS方法的抽样效率高于SRS方法.