最小超对称模型中希格斯势的真空稳定性

阎贲，冯太傅

(河北大学 物理科学与技术学院，河北 保定 071002)

标准模型(SM)已经在科学家们的持续深入研究中暴露出越来越多的不足之处，希格斯势的真空稳定性正是这些问题之一：SM的希格斯势由于受到top夸克的负的辐射修正，在场值足够大的区域是不稳定的[1]，这需要新物理模型的改进.MSSM在SM的基础上引入了互为超对称伴的费米子和玻色子[2]，在场论计算中它们的辐射修正符号相反，可以在一定程度上互相抵消.这样，MSSM应当能改善SM中存在的真空稳定性问题.

1 有效势的一般讨论

在量子场论中，有效势V(φ)定义为有效作用量Γ(φ)的动量展开式中的零级项，在坐标空间这个展开表示为

(1)

其中φ表示经典场，给出V(φ)的傅里叶变换式

(2)

展开系数Γ(n)是具有n条外线的所有单粒子不可约费曼图的和[3].对于物理模型，有效势的微扰展开可以表示为[4]

(3)

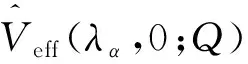
2 有效势圈修正与重整化

有效势圈修正与重整化密不可分.场论中的有效势为哈密顿量的非导数部分，外腿的动量设为零后，有效势对应物理的经典势.因此有效势(3)应与标度参数Q无关，如下微分等式恒成立:

(4)

这就是重整化群方程.它意味着改变标度参数Q对有效势带来的影响全部由耦合参数λi以及场φ的变化补偿.λi和φi随标度Q的变化分别由β函数与反常维γ函数描述，其中β函数可以通过定义t≡lnQ表示为

(5)

(6)

其中mi=mi(φu,φd)是由模型中各粒子质量矩阵所确定的依赖于希格斯场的质量本征态；Q对应重整化群方程中的标度参数；系数ni的绝对值对应每个粒子的质量本征态的简并度，正负号取决于粒子自旋，费米子为负，玻色子为正.

3 MSSM希格斯有效势

在单圈阶考虑MSSM中的希格斯有效势，它是树图势与单圈修正势的和

(7)

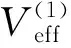
(8)

其中hu、hd代表中性的希格斯场，为方便研究对中性场平移，分离出希格斯标量场φu、φd，赝标量场σu、σd和真空期望值νu与νd.

(9)

对Veff应用中性希格斯场取真空期望值时势为极值的最小化条件

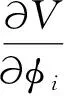
(10)

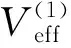
对(7)式应用Bμ、|μ|2的约束条件后得到单圈修正的希格斯有效势，为研究这个有效势在不同能标下的行为，还需要考虑重整化群能标Q跑动的影响.(7)式中含有耦合因子λi和希格斯标量场φi，将其替换为由β函数与γ函数所确定的λα(Q)和φi(Q)，最终得到MSSM模型中单圈修正的有效势Veff(λα(Q),φi(Q);Q).下一节将分析有效势在任意能标Q下随场φi的变化是否形成稳定的势阱，以及稳定势对的参数空间的要求.

还有1个问题会影响分析计算，是所谓有效势凸性问题.有效作用量Γ(φ)定义为生成泛函W[J]的勒让德(Legendre)变换，它一定是凸函数[8](凸函数在文中指具有二阶导数大于零这种下凸的形状的函数，与国内一些数学教材的定义相反).因此，有效势Veff也是φ的凸函数.问题很明显，凸势不能导致自发对称破缺.据Dannenberg的讨论[9]，凸性问题正是计算中遇到的复数项的问题：任意的φ场取值会导致mi(φi)出现复数值的本征值从而有效势为复数，有效势的复数值正是在其非凸的区域产生.对于复数有效势的物理意义，在单圈阶有很好的解释：它的实部给出势能期望值，虚部给出单位势能强度的衰变率[10].由于讨论的问题只涉及势能期望值，所以在后面的数值部分对有效势一致地取实部以简化分析计算.

4 MSSM希格斯势的真空稳定性分析

模型参数的初始取值的能标被设定在超对称能标1 TeV，这些初始取值满足各种物理实验数据的限制.当重整化群能标Q向高能演化时，所有λα(Q)的取值，通过被初始值确定的β函数给出，希格斯标量场φu(Q)和φd(Q)由γ函数重新标度.这些β函数构成庞大的微分方程组，借助于计算机软件Mathematica以及程序包SARAH[11]，可以在双圈阶将其数值解出.对模型参数取值有约束的实验限制主要为希格斯粒子质量(125.10±0.14)GeV的限制[12].为满足实验限制，可调参数的初始值如下：

(11)

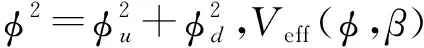
可以看到β在0.83附近时，势在大场值处失去势阱形状变得不稳定，精确的坐标读数显示稳定势对β的限制为β>0.865或tanβ>1.17.

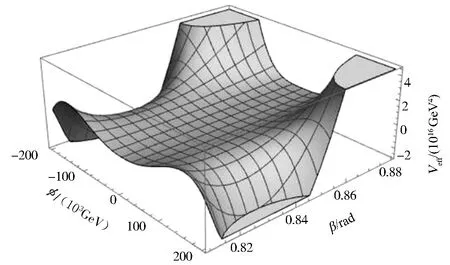
图1 Veff(φ,β)的函数关系Fig.1 Diagram of Veff(φ,β)

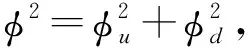
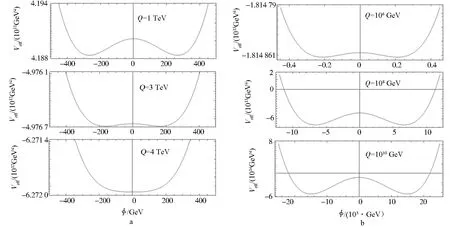
a.Q从1 TeV增加到4 TeV；b.Q从106 GeV增加到1010 GeV.图2 Q增加时Veff(φ) 行为示意Fig.2 Schematic diagram of the behavior of Veff(φ) with Q increasing

Veff(φ)随Q的演化大致分为2个阶段：Q从1 TeV增加到4 TeV的过程以及Q大于4 TeV的增加过程.图2a描绘了Q从1 TeV增加到4 TeV的阶段中Veff(φ)的变化，3个子图具有相同φ的场范围和势能间隔.可以看到，产生自发破缺的中央隆起区域的大小随Q的增加慢慢减少，约在Q=4 TeV时完全消失.这个隆起受2个因素影响：1)树图势中正负号相反的二次项的系数与四次项系数；2)圈修正势的辐射破缺效应.图2a隆起区域减小的原因分析为：在Q从1 TeV到4 TeV的较低能标范围内，树图势的贡献起主导作用，而树图势中负的二次项的系数，随着Q的增加而增加，在约为4 TeV的时候消失为0.

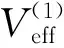
(12)

其中A和B分别正比φ的四次项和二次项系数，函数Productlog是定义在区间[-1/e,+∞]上的xex的反函数.对通常的树图势A是正实数，则上式+号项成为Q的增函数.因此，随着能标Q增加中央隆起的区域持续增加.

5 结论

超对称模型是被科学家们广泛看好的新物理模型.真空稳定性则是超对称模型中的重要课题.通过将场论对有效势和重整化群的一般分析应用在MSSM中，以及借助计算机数值计算双圈阶重整化群方程的解，研究了单圈修正的希格斯标量势在不同能标下的真空稳定性表现.结果显示在1 TeV的超对称能标下，圈修正的希格斯势对tanβ的取值给出了不同于树图阶的限制.随着能标的增长，希格斯势的行为出现了有趣的变化.分析了这种有趣变化的原因，也证实了得益于超对称伴粒子的贡献，希格斯势并没有像标准模型那样在大场值区域变得不稳定.