超高速正撞击下弹丸形状效应对碎片云分布特征的影响规律*
彭芸, 邓勇军, 刘筱玲, 姚勇, 黄洁
(1. 西南科技大学土木工程与建筑学院, 绵阳 621010;2. 中国空气动力研究与发展中心超高速碰撞中心, 绵阳 621010)
1 引言
为了更好地提高航天器在空间碎片环境中的生存机率, Whipple 在1947 年提出一种能够显著提升航天器抵御空间碎片撞击能力的防护结构[1]。 该结构是在舱壁外设置一道防护屏来破碎入射物体形成碎片云并使其充分扩散, 从而将单个碎片对舱壁的点撞击转化为碎片云对其的面撞击, 以此来降低对舱壁的损伤。 因此, 碎片云的形貌、 速度、 质量分布等特征直接决定着碎片云对舱壁 (Whipple 防护结构后板, 后统称 “后墙” ) 的侵彻能力, 进而决定在轨航天器的安全可靠性以及指导航天器的防护结构设计。 另一方面, 真实空间碎片(撞击试验中称为“弹丸” )往往不是单一的形状, 存在如球形、 圆柱体(含圆盘形、 长杆形) 或长方体等多种形状。 不同弹丸撞击防护屏(Whipple 防护结构前板, 后统称“薄板” ) 产生的碎片云形状、 碎片大小、 数目及速度分布都不尽相同[2-4], 因此对于评估在轨航天器的安全性能以及指导空间防护工程的设计, 开展弹丸形状效应对超高速撞击产生的碎片云分布特征的影响研究十分重要。
由于超高速碰撞时间极短, 在碰撞过程中产生的碎片云颗粒在形状、 大小、 速度上的分布特征很难通过试验获得。 尤其当撞击速度达到7km/s以上时, 试验要求更高, 数据采集难度更大。 而数值模拟方法对于研究超高速碰撞下碎片云分布特征则优势十分明显[5]。 限于有限元在计算高应变率问题时出现的单元畸变、 单元失效删除带来的能量损失等问题, 研究者提出可以用无网格的光滑粒子流体动力学 ( Smoothed Particle Hydrynamics, SPH) 方法[6-8]或无网格法与有限元耦合[9,10]的算法来数值模拟超高速碰撞下的碎片云。 SPH 方法是一种Lagrange 无网格粒子算法, 通过使用一系列任意分布的节点或粒子来求解问题。 与传统有限元方法相比, SPH 方法更适用于处理大变形问题, 且更容易推广到多尺度计算与非连续介质计算, 非常适合用来计算空间碎片超高速撞击的问题[11]。 1991 年Libersky 等[6]率先将材料强度引入SPH 方法并完成了高速撞击的数值模拟。 随后研究者[12-17]对SPH 方法开展了大量的研究工作, 不断完善和发展SPH 方法在空间碎片超高速撞击问题中的应用, 开展了靶厚[12,14,17]、 弹速[12,13,15,17]、 形状[12,14,15]、 撞击角度[13]、 材料模型[14,16]等对碎片云外貌形态、 速度分布、 质量分布等特性的影响研究。 目前考虑弹丸形状及尺寸的影响, 仅针对Piekutowski 的试验[2-4]进行了模拟分析, 还未进行规律性的影响分析。 本文基于商业软件AUTODYN 中的SPH 方法对不同弹丸超高速正撞击典型Whipple 结构的薄板进行了数值模拟, 分析研究不同弹丸形状、尺寸对碎片云分布特征的影响。
2 碎片识别
当弹丸超高速撞击并穿过薄板时, 弹丸材料和薄板材料会破碎形成碎片云, 如图1 所示, 数值模拟能较好地反映碎片云的组成和来源。 研究表明[2,17], 薄板材料在撞击一侧喷射小碎片形成的反溅碎片云, 弹丸穿过薄板后薄板材料向外扩散的外泡碎片云, 以及弹丸尾部材料破碎剥落而成的剥落碎片云对后墙的破坏能力均相对很弱。因此, 在本文碎片云的特性分析中, 主要针对弹丸破碎后形成的主体碎片云, 该部分云团中各碎片的质量和尺寸均较大, 对后墙有较大威胁, 具备较强的侵彻能力。 本文基于AUTODYN 软件的碎片识别及显示模块, 根据计算中设置的材料失效准则, 判断SPH 粒子点是否材料失效, 认为孤立碎片的边界由失效粒子构成, 且计算中设定的SPH 粒子点即为所能模拟的最小物质单元, 不可再分割及破坏, 这符合在实验中小尘埃难以观测的事实, 因此该碎片识别技术能够很好地展示模拟得到的碎片分布结果。 综合碎片材料是否失效、 碎片质量和尺寸大小, 对碎片云团进行识别, 如图2 所示, 从中开展板后碎片云空间扩展曲线、 质量分布、 速度分布等碎片云分布特征的影响分析。

图1 碎片云外貌形态及结构Fig.1 Shape and structure of debris cloud
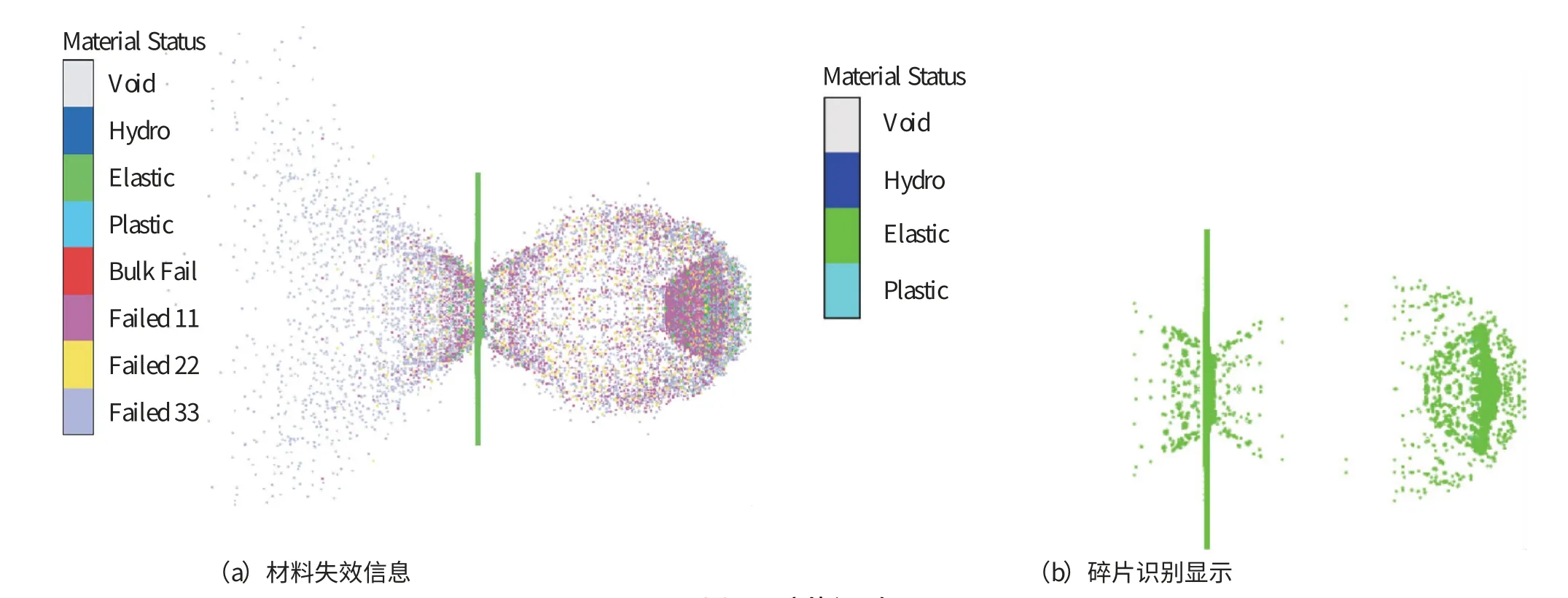
图2 碎片识别Fig.2 Debris identification
3 方法验证
本文参考文献[17] 中实验编号05 工况,球形弹丸直径D=6.35mm, 板厚t=0.5mm, 撞击速度为v0=5km/s, 比较在同一时刻7.02μs 的数值模拟与实验的结果。 图3 (a) 为7.02μs 时刻数值计算的碎片云形态, 经碎片识别后筛选得到材料未失效的危险碎片如图3 (b) 所示, 并与实验照片图3 (c) 进行对照比较。 从图中可以看出, 数值模拟结果与实验照片相似, 主体碎片云的碟状形态已形成, 即中间厚, 两边缘稍薄; 后剥落碎片云隐约可见。 根据关键点(最前端点1、边缘点2) 的速度信息v1a和v2a进行比较, 从表1中可以看出计算结果与实验结果的误差在5%以内。 由此说明, 本文采用的计算方法用来识别并分析碎片云的分布特征是可行的。

图3 模型验证结果Fig.3 Model verification result

表1 v1a 和v2a 的数值模拟与实验结果对比Table 1 Comparison of numerical simulation and experimental results of v1a and v2a
4 计算模型
基于碎片云的复杂特性, 本文利用SPH 方法对超高速撞击薄板产生的碎片云进行了大量的数值模拟, 以便能得到弹丸形状效应对碎片云分布特征的规律。 本文计算模型如图4 所示, 考虑薄板材料为AL6061-T6, 尺寸为50mm×50mm×0.5mm。 弹丸材料为AL2A12 (即LY12), 弹丸形状考虑球形、圆柱体、 长方体和三棱柱, 弹丸撞击速度范围为3~7km/s。 考虑到计算速度和精确度, 粒子大小取0.1mm, 计算时间t=10μs。

图4 计算模型Fig.4 Calculation model
弹丸和薄板均采用 Steinberg-Guinan 强度模型、 Shock 状态方程、 Grady-Spall 失效模型。 结合文献[16]、 [17], 采用的材料参数分别如表2 和表3 所示。

表2 Steinberg-Guinan 强度方程参数Table 2 Parameters of Steinberg-Guinan strength equation

表3 Shock 状态方程参数Table 3 Parameters of Shock state equation
Grady-Spall 失效模型[16]基于主应力判断失效, 即主应力超过失效阈值σs后材料失效, 失效阈值σs可由公式得到:
式中:ρ为材料密度, 可由材料的连续性方程或核函数更新得到;Y为材料屈服强度, 可利用材料强度模型根据材料当前应变、 应变率和温度计算更新得到, 但变化幅度较大, 对σs计算值影响严重;C0为材料声速, 可由材料弹性常数和当前密度确定;εc为临界失效应变, 材料常数, 铝合金材料一般取0.15[16-18]。
5 碎片云分布特征
碎片云的形貌、 质量、 速度等分布特征直接决定着碎片云对后墙的侵彻能力, 本文考虑弹丸不同尺寸、 形状(球形、 圆柱体、 长方体和三棱柱, 如表4 所示) 对板后碎片云外貌形态、 径向扩展曲线、 碎片数目分布、 质量分布、 速度分布等特征开展分析。

表4 弹丸型号及尺寸Table 4 Projectile types and sizes
碎片云外貌形态主要是考虑在不同撞击条件下, 板后碎片云整体结构在形状上的不同。 经碎片识别后用碎片云径向尺寸, 如图5 所示, 随时间的变化来获得径向扩展曲线, 表征碎片云在空间的扩散情况, 反映碎片云径向膨胀程度, 以便分析后墙的受损区域大小[18]。

图5 碎片云尺寸示意图Fig.5 Schematic diagram of debris cloud size
研究[18]发现, 碎片云中一些较大的碎片会直接影响后墙的受损程度, 即弹孔情况。 本文参考文献[19], 假设Whipple 防护结构后墙(即舱壁) 的厚度为2.5mm, 定义以弹丸初始撞击速度能穿透该后墙(同薄板材料且2.5mm 厚) 的碎片为危险大碎片。 通过对危险大碎片的数目、质量、 速度等进行环状分区统计, 来评估碎片云对后墙的侵彻能力。 如图6 所示, 距弹丸撞击处中心O 点, 沿碎片云径向划分5 个区域进行统计碎片云的分布情况: I 区(距中心O 点0 ~4mm)、II 区 (4 ~8mm)、 III 区 (8 ~12mm)、 IV 区(12~16mm) 和V 区(大于16mm)。 结合文献[1] 和[20], 利用球形弹丸撞击单层板的弹道极限方程进行估算, 并结合数值计算结果, 确定在不同撞击速度下穿透2.5mm 厚后墙的碎片临界尺寸, 如表5 所示。 本文的碎片环状分区统计只提取特征长度大于或等于碎片临界尺寸的危险大碎片来分析比较碎片云对后墙的潜在威胁。

图6 环状统计示意图Fig.6 Circular statistical diagram

表5 危险大碎片的临界尺寸Table 5 Critical dimension of large hazardous debirs
5.1 球形弹丸尺寸的影响
5.1.1 相同撞击速度的初始条件
在弹丸形状和撞击速度(v=5km/s) 都相同的条件下, 碎片云外貌形态受弹丸尺寸的影响差别不大, 但碎片识别后差异明显, 如图7 所示。外泡碎片云: 球形弹丸均呈球面, 大直径6mm 弹丸SD6 的碎片云轮廓最清晰, 小直径3mm 弹丸SD3 破碎完全, 轮廓最模糊; 主体碎片云: 弹丸SD5 和SD6 的碟形(中间厚, 两边薄) 明显, 随着球形直径的增加, 碎片分布相对越来越密集、碎片的质量越来越大; 后剥落碎片云: 弹丸SD4、SD5 和SD6 尾部材料的破碎剥落较为明显。

图7 碎片云受弹丸尺寸影响(t=10μs)Fig.7 The debris cloud affected by the size of the projectile (t=10μs)
图8 为碎片识别后材料未失效的碎片云空间扩展径向尺寸随时间变化的曲线。 在相同弹丸形状、 撞击速度条件下, 径向扩展尺寸随着弹丸尺寸的增加而有所增大, 即对后墙产生损伤的区域亦会变大。 其中SD4、 SD5 和SD6 的径向扩展差距较小, 即对后墙产生损伤区域的影响区别不明显。
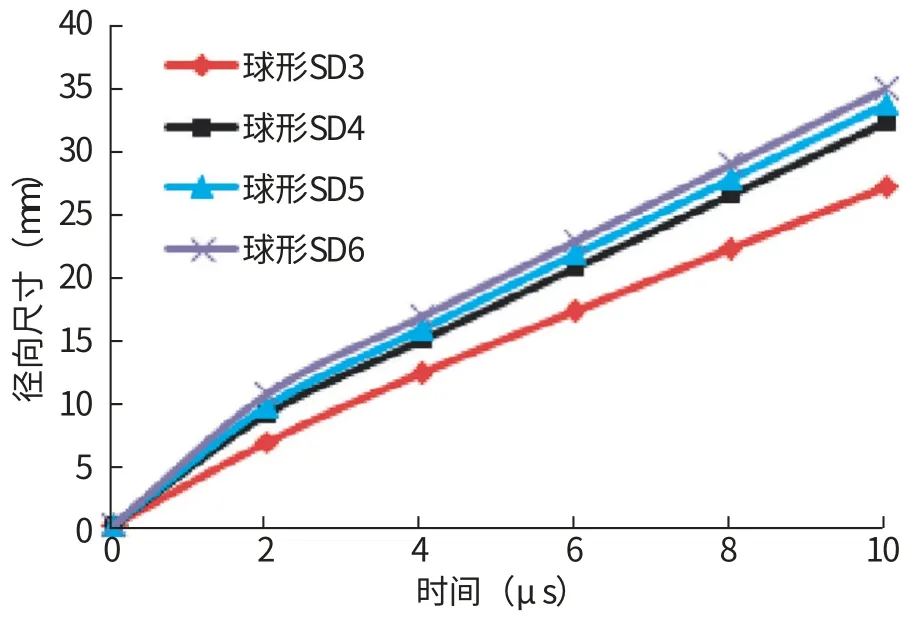
图8 碎片云径向扩展曲线Fig.8 Radial expansion curves of debris cloud
根据表5 的碎片临界尺寸, 对超高速撞击后材料未失效且板后特征长度不小于1mm 的危险大碎片进行环状区域分布统计, 以此来比较分析碎片云对后墙的侵彻能力。 表6 列出了各球形弹丸的碎片总数目和危险大碎片数目。 其中, 弹丸SD3 撞击后材料未失效的碎片总数目为699 个,但由于弹丸破碎彻底, 碎片特征长度均小于撞击速度为5km/s 时的碎片临界尺寸(1mm), 即危险大碎片数目为0。 大尺寸弹丸SD6 的危险大碎片数目最多, 高达124 个, 对后墙穿孔的威胁最大。

表6 危险大碎片数目统计Table 6 Statistics on the number of hazardous large debris pieces
图9 分别给出危险大碎片的数目、 质量和撞击薄板后剩余速度在各分区中的分布情况, 统计各区域危险大碎片数目、 质量和剩余速度的最大值、 最小值及平均值。 除SD3 无危险大碎片外,其余球形弹丸的危险大碎片都集中在I、 II、 III区。 碎片越靠近撞击中心, 其质量越大。 SD4、SD5 和SD6 产生的单个碎片质量最大分别为4.0mg、 18.0mg 和31.9mg, 且均位于I 区, 剩余速度分别为4.62km/s、 4.69km/s 和4.73km/s。总体来说, 随着球形弹丸直径的增加, 危险大碎片的数目、 质量、 速度均有增大, 即对后墙的侵彻能力亦在提高。

图9 碎片云分布统计Fig.9 Debris cloud distribution statistics
5.1.2 相同撞击动能的初始条件
在相同初始动能条件下, 碎片云形态受弹丸撞击速度的影响非常明显, 如图10 所示。 球形弹丸均有明显的球面形状的外泡碎片云; SD6 的主体碎片云最为密集且单个碎片的特征长度及质量均最大, 而SD4 的分布最为分散和均匀; SD5 的后剥落碎片云清楚可见, SD6 因撞击速度较低,弹丸尾部材料破碎不严重, 未形成后剥落碎片云。

图10 碎片云受弹丸速度影响(t=10μs)Fig.10 The debris cloud affected by the velocity of the projectile (t=10μs)
从图11 碎片云径向扩展曲线可以看出, 在相同撞击初始动能条件下, 弹丸尺寸越大, 则撞击速度越小, 径向扩展受速度的影响非常明显。 三种球形弹丸中, 尺寸最大的SD6, 由于撞击速度比SD4、 SD5 小得多, 其径向尺寸也较之小得多,则后墙受损区域会相对较小。

图11 碎片云径向扩展曲线Fig.11 Radial expansion curves of debris cloud
根据表5 确定不同弹丸撞击速度下碎片的临界尺寸, 对各弹丸产生的碎片云进行筛选。 从表7 中碎片的总数目可以看出, 碎片总数目受弹丸速度影响明显, 速度越大, 弹丸越容易破碎完全, 碎片数目增多。 弹丸SD4 和SD6 比较, SD4的质量虽不足SD6 的30%, 但其危险大碎片的数目比SD6 的数目多1 倍。 需要注意的是弹丸SD6撞击后危险大碎片的数目虽然最少, 仅为10 个,但由于撞击速度较低, 弹丸材料破碎不完全, 单个碎片的质量最大值高达254mg, 如图12 所示。从对危险大碎片在各分区的数目、 质量和速度统计结果来看, 球形弹丸的碎片分布较为集中, 仍在I、 II、 III 区, 且各弹丸的最大质量碎片均在距撞击中心最近的I 区。 从计算结果可以看到, 在相同动能条件下, 三种尺寸下的球形弹丸, 大尺寸SD6 对后墙的侵彻能力仍是最高。

表7 危险大碎片数目统计Table 7 Statistics on the number of hazardous large debris pieces

图12 碎片云分布统计FIg.12 Debris cloud distribution statistics
5.2 圆柱体弹丸尺寸影响
5.2.1 相同撞击速度的初始条件
在相同初始动能和撞击速度(5km/s) 条件下, 圆柱体弹丸的碎片云外貌形态受长径比的影响比较明显, 如图13 所示。 圆柱体弹丸的外泡碎片云均成圆锥面, 撞击面较大、 长径比较小(H/D=2/3) 的C6H4 圆锥面更为明显; 撞击面较小、 长径比较大(H/D>2) 的C4H9 和C3H16由于薄板材料破碎严重, 锥面不明显。 主体碎片云: 均成扁平状, 撞击面大的C6H4 碎片扩散较之更远、 更分散。 后剥落碎片云: 弹丸C6H4 后部材料破碎, 可见后剥落碎片云; 而长径比大于2的C4H9 和C3H16 弹丸穿透薄板, 其后部未完全破碎, 弹丸尾部直接穿过薄板, 成为大尺寸碎片。从图14 碎片云径向扩展曲线可以看出, 在相同初始动能和撞击速度条件下, 碎片云的径向扩展随长径比的增加有2mm 以内的增大, 即影响后墙受损区域的大小差别不大。 但是产生的危险大碎片受其影响明显, 从表8 危险大碎片的数目可以看出, 在相同初始动能和撞击速度条件下, 弹丸撞击面越小(长径比H/D越大), 危险大碎片数目越少, C3H16 仅有20 个。 但是由于圆柱体C4H9和C3H16 柱高较大, 在超高速撞击中, 弹丸并未完全破碎, 其尾部会作为一个特大碎片对后墙的安全性能有极大威胁。

图13 碎片云受撞击面影响(t=10μs)Fig.13 The debris cloud affected by the impact plane (t=10μs)

图14 碎片云径向尺寸Fig.14 Debris cloud radial dimensions

表8 危险大碎片数目统计Table 8 Statistics on the number of hazardous large debris pieces
如图15 所示, 在相同初始动能和撞击速度条件下, 圆柱体弹丸C4H9 和C3H16 撞击后产生的危险大碎片分布更集中(I、 II、 III 区内), 大质量碎片主要分布在I 区, 剩余速度的变化在II 区和III 区有较大波动。 其中弹丸C3H16 撞击后产生的危险大碎片质量大(最大为234mg) 且分布集中。 而弹丸C6H4 的碎片分布相对较分散、 更均匀, I 区最大碎片质量为3.7mg, 各区碎片质量均在0.1mg 以上, 剩余速度平均值高于3km/s。

图15 碎片云分布统计Fig.15 Debris cloud distribution statistics
5.2.2 相同撞击面积的初始条件
在相同初始动能和弹丸撞击面的条件下, 圆柱体弹丸撞击薄板后碎片云的外貌形态如图16 所示, 外貌形态受长径比的影响非常明显。 圆柱体弹丸的外泡碎片云前端成圆锥面, 其中C6H4 和C6H6 的圆锥面相对更为明显。 C6H4 和C6H6 扁平状主体碎片云特征明显, 且碎片扩散较远、 较分散, 后剥落碎片云明显可见。 而C6H8 和C6H10 由于弹丸穿透薄板后, 弹丸并未完全破碎, 弹丸尾部材料直接穿过薄板, 成为大尺寸碎片。
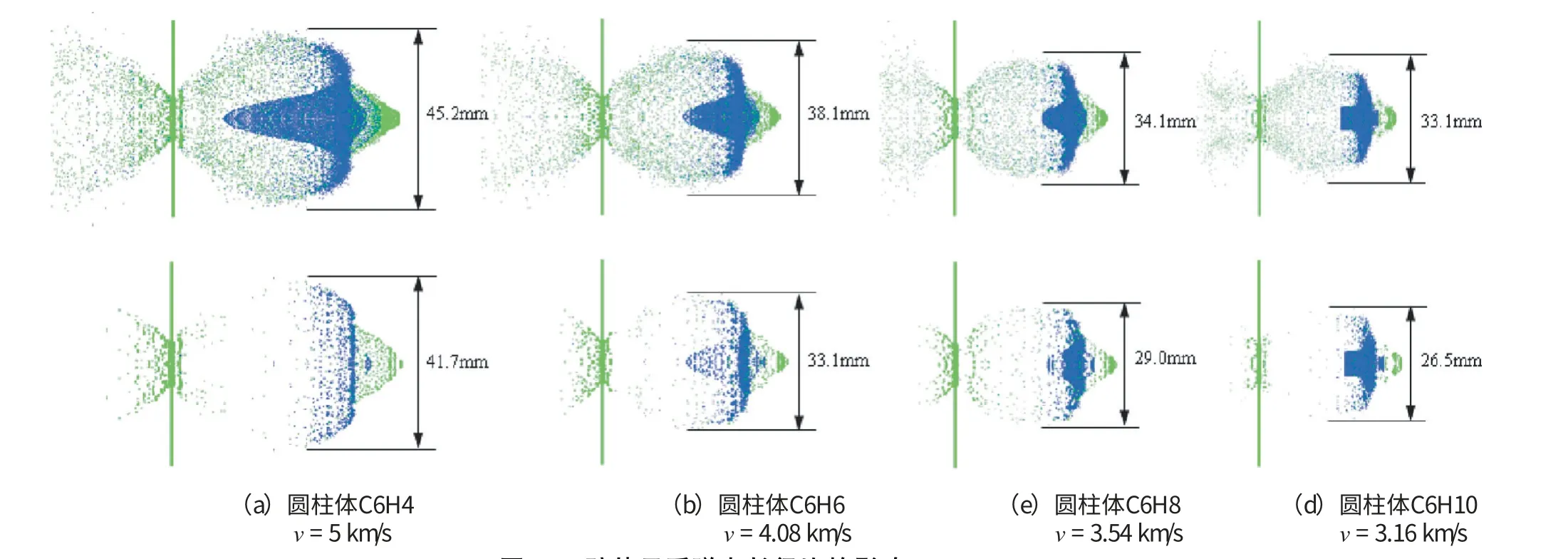
图16 碎片云受弹丸长径比的影响(t=10μs)Fig.16 The debris cloud affected by the slenderness ratio of the projectile (t=10μs)
碎片云的径向扩展曲线如图17 所示。 C6H4圆柱体弹丸的碎片径向尺寸最大, 径向分布最广。 在相同初始动能条件下, 圆柱体弹丸的底面尺寸不变, 随着长径比的增加, 碎片云的体积随之增大, 撞击薄板速度随之减小, 因此碎片云的径向尺寸受速度影响随之逐渐减小。

图17 碎片云径向尺寸Fig.17 Debris cloud radial dimensions
根据表5 的碎片临界尺寸确定表9 中各弹丸的危险大碎片数目。 从表9 可以看出, 在相同初始动能和撞击面积条件下, 长径比为1 时的弹丸C6H6 产生的危险大碎片数目最多, 为141个。 由于弹丸C6H8 和C6H10 并未完全破碎,存在尺寸和质量较大的危险碎片, 所以其碎片数目较少。
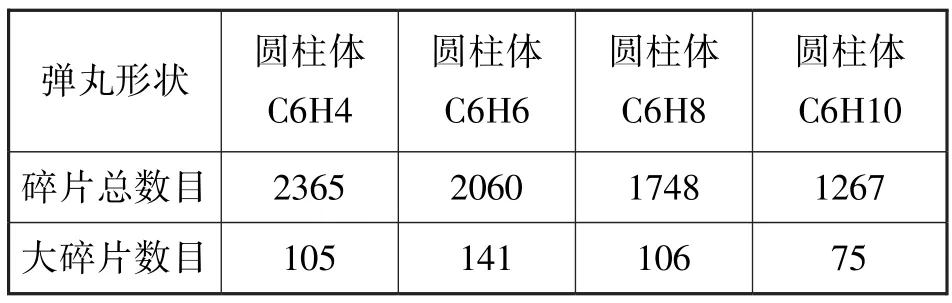
表9 危险大碎片数目统计Table 9 Statistics on the number of hazardous large debris pieces
从图18 碎片分布统计可以看出, 圆柱体弹丸危险大碎片的分布整体呈分散且较均匀的形式,各弹丸产生的最大质量碎片均在I 区, 且大质量1mg 以上的碎片仅分布在I、 II 和III 区。

图18 碎片云分布统计FIg.18 Debris cloud distribution statistics
5.3 柱体弹丸形状的影响
由图19 可知, 在相同初始动能、 弹丸撞击面积和撞击速度(5km/s) 的条件下, 碎片云形态仅受弹丸撞击面形状的影响明显。 其中, 外泡碎片云: 圆柱体、 长方体和三棱柱均呈圆锥面; 主体碎片云: 圆柱体和长方体呈扁平状, 碎片扩散较远、 较分散, 且关于撞击速度方向对称分布,而三棱柱由于弹丸形状非对称, 其碎片非对称分布且扁平状特征不明显; 后剥落碎片云: 仅圆柱体和长方体少量存在。
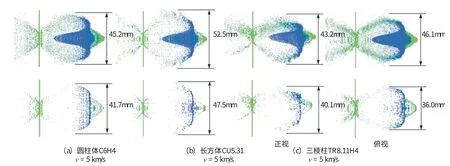
图19 碎片云受弹丸形状影响(t=10μs)Fig.19 The debris cloud affected by the shape of the projectile (t=10μs)
三种弹丸形状在超高速撞击后产生的碎片云径向扩展曲线如图20 所示。 圆柱体和长方体弹丸在撞击薄板初期(0 ~3μs) 的碎片云径向扩展曲线重叠, 变化趋势一致。 3μs 后圆柱体弹丸的径向尺寸逐渐向三棱柱靠近, 最终长方体弹丸的破碎更彻底, 碎片径向扩展更厉害, 对后墙受损区域的影响最大。

图20 碎片云径向扩展曲线Fig.20 Radial expansion curves of debris cloud
三种弹丸形状超高速撞击产生的危险大碎片总数目如表10 所示, 可以看出长方体弹丸产生危险大碎片云数目最多, 高达132 个; 圆柱体次之,为105 个; 三棱柱最少, 为98 个。 图21 将危险大碎片的数目、 尺寸、 速度进行分区统计, 柱体弹丸的碎片分布相对分散, 各区均有碎片。 圆柱体和长方体弹丸的大质量和高速度碎片主要集中在I 区和II 区; 三棱柱弹丸碎片分布则相对分散,各区均有质量大于1.5mg 且速度高于4km/s 的大碎片, 对后墙的受损范围和受损程度均有较大威胁。

表10 危险大碎片数目统计Table 10 Statistics on the number of hazardous large debris pieces

图21 碎片云分布统计Fig.21 Debris cloud distribution statistics
6 结论
本文采用软件AUTODYN 的SPH 计算方法研究了弹丸形状效应对超高速碰撞碎片云的影响,得出以下结论:
(1) 通过对球形弹丸、 圆柱体和长方体等弹丸的计算比较, 碎片云外貌形态、 碎片数目及其分布受弹丸几何尺寸和形状的影响较大。
(2) 相同初始动能条件下, 同形状的弹丸碎片云对后墙的侵彻能力随弹丸尺寸增加而提高。
(3) 圆柱体弹丸以相同速度撞击薄板时, 长径比对后墙受损区域大小(即碎片云径向尺寸)和受损程度(即弹孔情况) 均有很大的影响。
(4) 在相同撞击速度和长径比相当的条件下, 同质量的三棱柱弹丸碎片云质量大、 速度高且分布较分散, 对后墙的受损范围和受损程度均有较大威胁。

