像平面纠偏比例导引方法研究*

段耀武, 刘辉, 韩柠, 柳澍暄

(北京控制与电子技术研究所, 北京100038)

1 引言

在天文学上, 将轨道近日点距离在1.3AU(1AU=1.496×108km) 以内的小行星称为近地小行星(NEA)。 近地小行星的尺寸从只有几米的小“流星体” 到更大的直径几公里的天体。 当近地小行星“坠入” 地球大气层时, 直径较小的将无害地碎裂, 而直径较大的会造成局部或者全球破坏。 为了应对小行星撞击的风险, 需要建立有效的小行星防御系统。 目前美国、 俄罗斯等传统航天强国已经率先建设了近地小行星监测预警的相关基础设施, 我国也正在快速推动中国行星防御系统的建设和相关关键技术的攻关工作。 目前按照体系的布局分为: 监测预警、 在轨处置、 灾害救援、 国际合作四大板块。 其中在轨处置是实现主动应对小行星撞击风险的关键[1]。

应对小行星撞击风险的在轨处置方式主要可以分为两类: 一是瞬时作用, 利用动能撞击技术改变小行星轨道或利用核爆炸使小行星轨道偏转; 二是长期作用, 通过电推进来改变小行星轨道或利用激光烧蚀技术改变其轨道[2,3]。 当前,动能撞击是最为成熟的在轨处置手段。 美国继2005 年7 月4 日发射“深度撞击” (Deep Impact)探测器成功撞击了 Tempel-1 彗星之后, 于2021年在“深度撞击” 成功的基础上发射了“双小行星重定向测试” (DART) 航天器, 且于2022 年9月27 日在距地球1140 万千米处撞击双星小行星Didymos-Dimorphos 的次星Dimorphos, 成功地验证了动能撞击的可行性。 显然, 在深空尺度上实现对小目标的高精度、 高速撞击, 对制导控制系统提出了很高的要求, 而精确制导技术也是决定任务成败的核心关键。

深空高精度制导一般分为两种技术路线: 微分修正和比例导引[4]。 比例导引技术以其计算量小、 无迭代不收敛问题等优势受到国内外学者的广泛关注。 文献[5]针对深空撞击任务定轨精度差、 自主导航受限等特点, 推导了相对动力学方程, 并据此设计了一种满足需用角速度的脉冲比例导引律, 避免了自主导航精度对预测制导的限制。 文献[6]考虑到机动时机的选取以及最终撞击的精度, 针对小天体高速撞击任务的特点, 设计了一种脉冲比例制导的末段制导律。 该制导律引入点位误差椭圆来描述导航精度, 并基于深空撞击器离散脉冲控制力的特点, 以零控脱靶量落入误差椭圆的范围来控制轨控发动机的开关。 文献[7]提出一种卫星拦截器比例导引方法, 使用发射惯性坐标系中目标卫星和拦截器的实时绝对状态参数构造两者的相对运动参数, 设计一种改进比例导引方法以抑制视线转率。 文献[8]和[9]中采用的光学自主导航技术, 通过所拍摄的目标天体影像, 获得角度偏差, 并结合轨道动力学,运用非线性卡尔曼滤波方法实现撞击器定轨, 并得到撞击器的绝对空间位置后, 再进行制导解算, 撞击器的机动时间很大程度受限于滤波收敛速度, 制导指令的准确性受限于状态估计误差。上述研究虽较好地解决了它们各自所面对的具体问题, 但是也都存在一些不足。 最主要的问题在于: 传统的比例导引完全依赖于测量(或计算)的视线转率, 所以在面对视线变化缓慢的场景时(如本文中涉及的深空撞击任务的远距离段), 直接应用比例导引方法会带来较大的误差。

综上所述, 本文针对高速、 高精度深空撞击工程背景, 研究基于光学导航的像平面纠偏比例导引律。 优势在于: ①继承了比例导引计算量小、 不需使用滤波方法估计撞击器的绝对位置和速度的优点, 对撞击器的绝对状态不敏感, 缩短了制导指令生成时间, 避免了滤波收敛速度和估计精度的限制[10], 扩展了制导方法的适用范围;②在远距离目标位置变化难以观测的情况下, 通过增加改进项解决了比例导引方法完全依赖于视线转率实现目标跟踪的问题。 仿真结果表明, 本文提出的像平面纠偏比例导引方法能满足高精度撞击任务要求, 撞击角度能够最大程度保证设计要求和撞击效果, 为未来工程研制提供参考。

2 导引律设计

2.1 坐标系

J2000 日心黄道坐标系: 坐标原点O在太阳中心。 基本平面是历元J2000 对应的平黄道,X轴指向J2000 对应的平春分点,Z轴垂直于基本平面指向地球轨道面正法向,Y轴与Z轴和X轴构成右手直角坐标系。

建立撞击器本体坐标系:O -XbYbZb的原点定义在撞击器质心,Xb轴指向探测器头部,Zb轴位于撞击器纵向平面内指向垂直于Xb轴,Yb轴与其余两轴成右手坐标系。 相机固联于撞击器头部,相机坐标系与本体系重合。 发动机推力过撞击器质心, 可直接在±Yb、±Zb方向施加推力, 如图1所示。

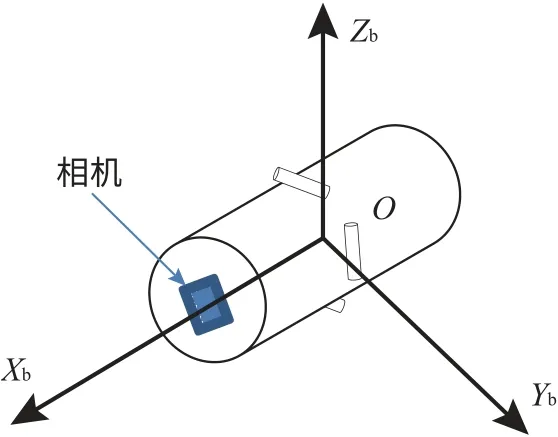
图1 撞击器本体坐标系Fig.1 Impactor body coordinate system

2.2 动力学模型

撞击器在飞行过程中, 受到太阳引力及其他大天体的引力、 太阳光压等干扰力。 撞击器在J2000 日心黄道坐标系下的动力学方程可表示为:

2.3 比例导引律

传统比例导引需要速度倾角去跟随视线角的变化, 使速度方向最终指向目标方向。 当深空中撞击器距离目标小行星较远时, 受视场角和焦平面的限制, 光学相机可能长时间捕捉不到像平面上目标点的变化, 进而也无法获得视线转率, 导致发动机也会长时间处于关机状态, 耽误宝贵的轨道机动时机, 最终导致误差偏大。

针对上述问题, 本文对传统的比例导引方法进行了适应性改进。 如图2 所示,y、z为目标小行星在撞击器本体坐标系YbO Zb平面的坐标,(vy,vz) 为目标小行星相对撞击器的速度在撞击器本体坐标系YbOZb平面的坐标。

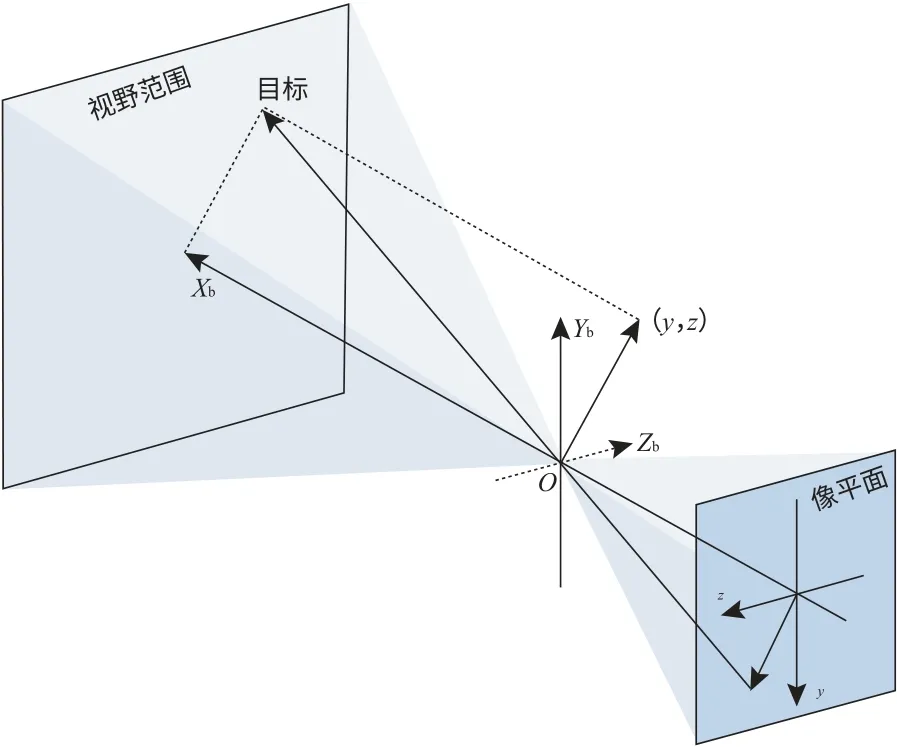
图2 撞击器本体坐标系下光学相机成像示意图Fig.2 Schematic diagram of optical camera imaging in the impactor body coordinate system

本文设计的像平面纠偏比例导引律的待增速度表示为

式中: 在Yb和Zb方向施加相应机动量k3vy、k4vz(k3、k4为比例系数) 是传统的比例导引分量,可以实现撞击器相对速度指向视线方向。 另外,增加的机动量可实现目标趋向于像平面的中心。τ为撞击器撞到目标小行星的剩余时间;ρ为撞击器到目标小行星的距离。 由于在深空撞击的末端vx变化可以忽略, 因此剩余时间k1～4为控制参数。 dy、 dz为光学相机捕捉到目标小行星在相机投影面的位置变化量, dt为相机采样时间,

2.4 控制参数选取

以Yb方向为例, 图3 给出式(2) 的闭环传递函数结构示意图, 其中PID 控制器传递函数

图3 等效控制系统结构示意图Fig.3 Structure diagram of equivalent control system

其中,k3的选取与传统的比例导引一致,k3∈[1, 4] ;k1保证在撞击时刻满足y =0。 图4中为τ=3000s 的示例, 此时k1=9。k2、k4选取原则与k1、k3相同, 不再赘述。

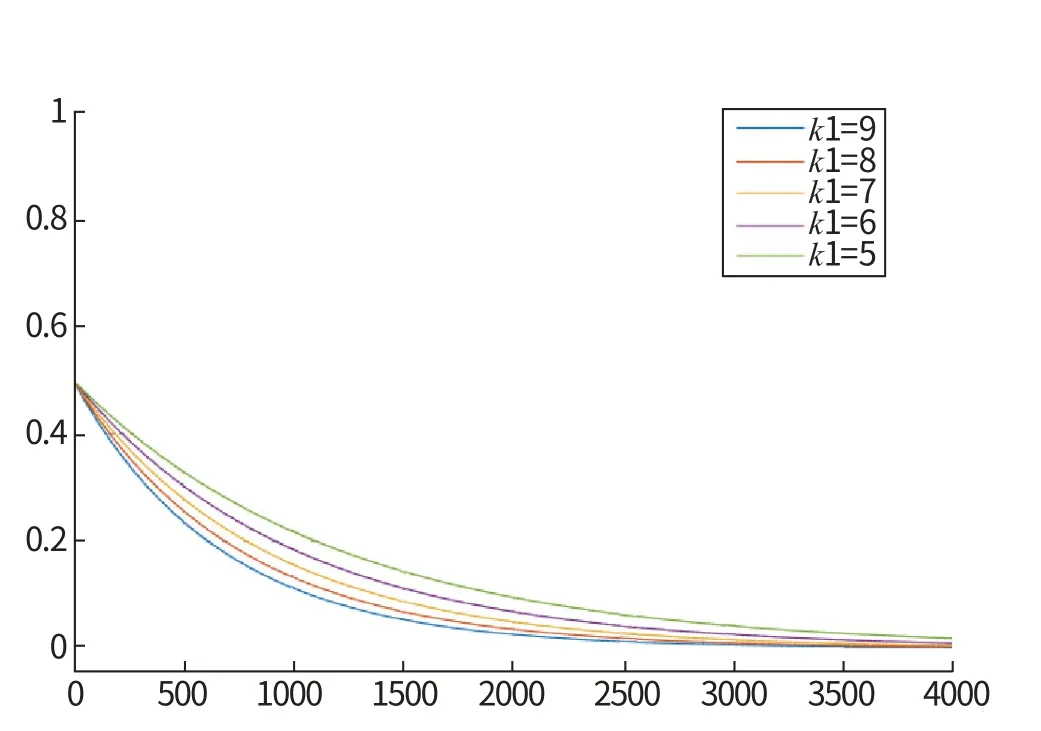
图4 控制系统时域响应曲线Fig.4 Control system time domain response curve

3 数学仿真分析

3.1 仿真参数

为了验证前述像平面纠偏比例导引的性能,本节选取了小行星Duende 为撞击目标天体进行数学仿真, 撞击器于2025 年11 月1 日发射, 并于2026 年8 月7 日第一次与Duende 小行星的轨道交会。 距交会剩余时间约1h、 相对距离约30000km 处开始制导实施撞击, 表1 给出了小行星Duende 的标称轨道, 表2 给出了撞击器的初始标称轨道, 表3 给出了综合仿真参数。

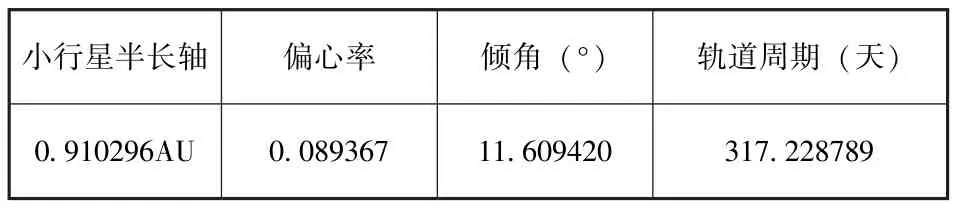
表1 小行星的标称轨道Table 1 The nominal orbit of the asteroid Duende

表2 撞击器的初始标称轨道Table 2 Initial nominal orbit of the impactor

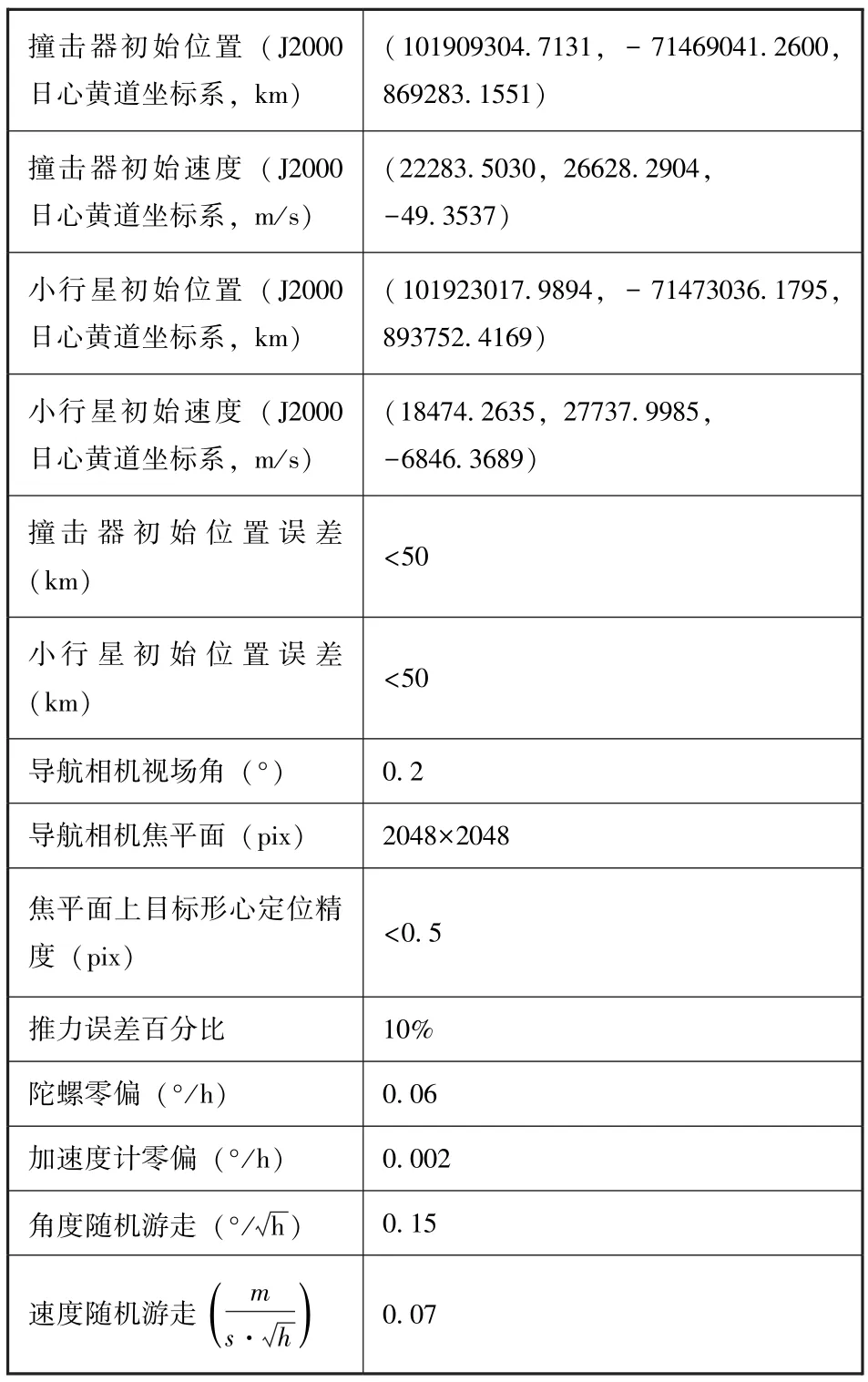
表3 综合仿真参数Table 3 Synthetic simulation parameters

3.2 仿真结果

首先, 在制导控制系统之前需要进行小行星目标的识别与导引。 目标识别与导引采用光学系统, 相关参数见表3 的导航相机部分。 目前直径30～50m 的NEA 是国际社会关注和应对防范的“重中之重”[1], 本文选取的Duende 平均直径为30m, 在20000km 处对应的像平面像素为1, 可以满足目标识别与精确导引的初始需求。 本文研究的重点在于制导律设计, 关于目标识别与导引部分不做赘述。

仿真计算采用像平面纠偏比例导引律式(2)。图 5 为撞击点在B 平面的位置分布, 其中实线为半径10m 的误差圆。 其仿真结果为CEP =1.9224m, 最大误差8.2893m, 满足最大误差小于10m。 能量消耗ΔV≤3.5m/s, 满足撞击器功耗要求。

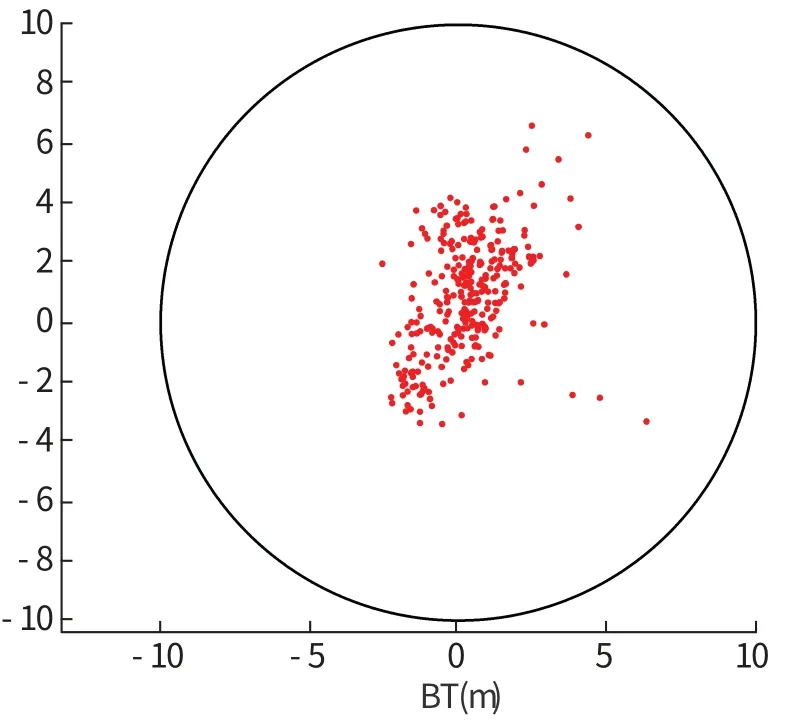
图5 撞击点分布Fig.5 Impact point distribution

图6 为撞击器最终撞击目标的撞击角度分布图, 采用了像平面纠偏比例导引律, 最终的撞击角度散布为0.0019° (1σ), 能够最大限度地保证撞击角度与设计值一致, 保证最佳撞击效果。

图6 最终撞击角Fig.6 The final impact angles

4 结论

本文针对深空撞击任务的特点, 设计了一种像平面纠偏比例导引律。 以Duende 小行星撞击场景为背景进行了数学仿真实验。 结果表明: 在表3 给定的光学系统条件下, 针对30 ～50m 直径小行星,像平面纠偏比例导引律能保证最大误差小于10m 的高速、 高精度撞击任务要求, 能量消耗ΔV≤3.5m/s,满足撞击器功耗要求。 且撞击角度散布很小, 能够最大程度地保证设计要求和最佳撞击效果。 另外, 相平面纠偏比例导引律适应能力强、 便于工程实现, 且在深空远距离条件下制导优势明显,可为未来工程研制提供参考。