考虑闲时对地遥感卫星的天基观测补网规划*

杨元, 祝开建, 侯重远, 郭伟娜, 常羽彤, 王志亮, 胡思才, 王蔚东

(1. 中国西安卫星测控中心, 西安 710043; 2. 中国人民解放军63768 部队, 西安 710600)

1 引言

天基观测是空间目标探测实现的重要途径。相比地基观测, 天基观测位置与空间目标的距离更近, 加之没有大气对信号的干扰, 其观测方法的分辨率更高[1]。 美国和俄罗斯已经发射数颗专用空间目标探测卫星用于以空间目标监视为核心任务的系统[2], 如美国的天基监视系统(Space Based Surveillance System, SBSS)、 轨道深空成像系统(Orbit Deep Space Imager, ODSI)、 空间跟踪与监视系统 (Space Tracking and Surveillance System, STSS)、 星历表精调天基望远镜(Spacebased Telescopes for Actionable Refinement of Ephemeris, STARE) 等。 这些天基监测系统都大大地拓展了空间目标的监视范围, 提高了空间目标的观测精度。

我国目前的空间目标监视设备大多为非专用设备, 多采用兼用的微小型空间目标监视平台[3]。 一类对地遥感卫星日常工作虽未安排天基监测任务, 但它们具有高分辨率、 高机动能力、多任务模式, 除满足对地成像需求外, 其软硬件性能同样具备空间目标监视能力。 以“吉林” 一号对地遥感星座为例, 近年来它们已完成了多次对惯性空间目标成像, 实现了对空间目标交汇成像定姿定轨的需求, 并验证了对地遥感卫星用于天基观测的可行性[4]。 可以说, 利用好这些对地遥感卫星不仅可以增加我国空间目标识别范围和空间监视网络的性能, 而且还可以进一步支持卫星编目和空间态势感知能力。

随着空间目标数量的不断增加, 现有观测资源明显不足, 势必需要优化空间目标监测计划,尽可能实现观测设备的充分利用, 这是当前空间目标监测系统中必须考虑的问题。 文献[5]针对多成像卫星联合调度规划问题, 建立了多星联合调度约束满足最优化模型, 提出了一种改进的差分进化算法有效地分配卫星资源。 文献[6]针对应急条件下成像卫星任务规划问题, 建立了面向任务需求的应急条件下单任务综合规划模型, 采用深度优先搜索算法分析了卫星、 测控及数传资源的分配问题。 文献[7]针对多个成像任务同时监视问题, 采用禁忌搜索算法与知识型蚁群算法相结合的策略则可实现以较快的速度获得较优的解。 文献[8]针对密集观测场景下敏捷成像卫星任务规划问题, 提出融合IndRNN 和Pointer Networks 的算法模型对敏捷成像卫星任务规划问题进行求解, 从而获得更高的观测收益率。 这些工作都在设备卫星资源不变的情况下, 针对不同规划需求实现了观测能力的较大提升。

不同于上述研究, 本文针对资源不足的条件下, 结合我国空间目标天基监测网的实际, 利用处于空闲时间的对地遥感卫星, 增加可监测资源数量, 建立一种考虑闲时对地遥感卫星的天基观测补网规划模型, 解决天基观测动态调度的可用性和稳定性。

2 天基观测补网的特点

目前对于天基观测规划的研究, 多是基于静态条件, 即假设观测调度一旦开始, 参与调度的任务和资源不再变化。 而事实上, 天基观测在一个十分复杂的环境中, 观测规划在执行过程中往往会出现各种扰动因素, 如卫星资源状态的变化、 新任务到达、 空间预警影响等, 这就使得天基观测网覆盖不全。 如果不顾任务动态变化, 仍用旧的调度方案将导致存在监测盲区; 如果抛弃初始调度方案, 在资源不增的条件下重新进行规划, 则变动规模较大时, 实时性要求很难满足,且容易打乱卫星后续任务安排。 因此, 相比于天基观测的日常规划, 补网规划特点有: (1) 补充原有观测资源的空缺, 尽能力完成全部任务, 提高任务的完成率; (2) 对原有调度方案的调整尽可能少, 保持规划的稳定性和重用性, 便于后续工作开展; (3) 主要针对动态应急任务, 在满足前两个特点的基础上, 以任务结束时间最早作为优化的第三层目标。

3 卫星资源空闲窗口与天基观测时间约束

3.1 卫星资源空闲窗口

对地遥感卫星是探测地球资源和环境的卫星, 当陆地资源卫星运行至海洋上空与海洋资源卫星运行至陆地和河流上空时就属于任务空闲期。 根据卫星最新的精轨根数在STK 软件和MTALAB 软件配合下可以求解未来一段时间卫星资源空闲窗口。 以某陆地资源卫星为例, 计算流程如下:

Step1: 利用MTALAB 中Mapping Toolbox 工具箱, 导入海岸线数据(load coastlines), 计算海洋与非海洋区域, 并绘制海岸线地图。 问题初始化, 在STK 中导入卫星最新精轨瞬根和载荷幅宽, 设置初值: 记录变量i =0, 卫星资源空闲窗口TL =0, 需要考虑时间段T0=(ta,tb) 。

Step2: 根据卫星的轨道根数, 利用STK 中HPOP 模型进行时间段为Ti轨道外推, 求星下点轨迹, 获得卫星时间与星下点经纬度的对应表A, 迭代i = i +1。

Step3: 采用微分法, 求解卫星星下点与海岸线相交点, 得卫星星下点临界经纬度, 查表A获得卫星处于海洋上空的时间窗口Ti o ={(t1a,t1b), …(tka,tkb), …(tna,tnb)} 。

Step4: 如果卫星在Ti时段内有机动计划, 变轨时段为Ci =(tca,tcb) , 本轮卫星处于资源空闲窗口Til:

满足(1)、 (2)、 (3) 三种情况之一卫星资源空闲窗口TL =TL +Til, 修改Ti =(tca,tb) , 获取机动策略中的控后轨道根数, 并转Step2; 否则转Step5。

Step5: 计算确定时间段T0=(ta,tb) 内卫星资源空闲窗口为TL = TL + Tio, 求解结束。

3.2 成像活动的时间约束

为了满足观测目标的可见和成像质量高, 成像活动需要考虑太阳、 地球、 空间目标和监测卫星空间几何关系和载荷性能要求两大类约束。 这些约束具有很强的时间依赖性, 可以转换为相应的时间约束。

①考虑地球遮挡的时间约束

当地球处在观测卫星与空间目标之间且位于二者连线上时, 空间目标不可见。 当满足公式(1) 时, 卫星可规避地球遮挡约束。

式中:rT(t) 为t时刻空间目标在J2000 惯性坐标系下的位置矢量,rO(t) 为t时刻观测卫星在J2000 惯性坐标系下的位置矢量,RE为平均地球半径。

②考虑地影的时间约束

空间目标必须在太阳光照射下才能清晰可见, 若目标进入地影区将导致成像质量灰暗, 难以辨别, 因此考虑地影的可见条件需满足公式(2) 或(3)。

式中:rS(t) 为t时刻太阳在J2000 惯性坐标系下的位置矢量。

③考虑太阳光干扰的时间约束

当逆向太阳光观测空间目标时, 由于背景光强烈, 导致成像质量模糊不清, 无法使用。 如公式(4) 所示, 当实际太阳光约束角大于观测设备的临界太阳约束角时, 拍照不会造成成像效果曝光过度。

式中:θsum,min∈(0, π/2) 为观测设备的临界太阳约束角。

④考虑视场角的时间约束

由于观测设备有视场限制, 空间目标的可见条件是观测角小于观测设备的最大视场角。 设因此满足公式(5) 时, 空间目标才在卫星视场角范围内。

式中:rL(t) 为t时刻观测设备光轴在J2000 惯性坐标系下的位置矢量,θsight,max∈(0, π/2) 为观测设备的最大视场角。

⑤考虑观测距离的时间约束

由于观测星等有限, 因此对给定尺寸的空间目标的探测距离有限。 观测卫星的最大探测距离如公式(6) 所示, 可以由给定观测星等与空间目标等效横截面积确定。 监视卫星与目标相对距离必须小于观测卫星对给定目标的最大探测距离, 即满足公式(7)。

式中:D为卫星最大成像距离,L为观测星等,S为观测对象等效横截面积, ΔR(t) 为监视卫星到目标相对距离。

⑥考虑相对角速度的时间约束

由于观测星与空间目标在惯性空间都非静止不动, 两者相对运动过大将会导致成像任务失败[9]。 如公式(8) 所示t时刻目标与监视卫星的相对角速度大小Δω(t) 不能超过观测设备能识别的最大相对角速度Δωmax, Δω(t) 的计算方法如式(9) 所示。

式中:Δv(t) 为目标与监视卫星的相对速度矢量,ΔvT(t) 为Δv(t) 切向分量。

综上所述, 在卫星成像活动时间窗口TP内,有∀t∈TP, 使得公式(1)—(10) 成立, 则观测卫星可获得可见的高质量目标图像。

3.3 卫星工况引起的时间约束

①姿态转换时间

在卫星机动方面, 为了尽可能使空间目标在观测设备的视场角内, 卫星平台或星上载荷可以通过侧摆、 俯仰和偏航三个自由度方向的轨道姿态机动开展成像活动[10]。 姿态机动最大需求时间可用公式(11) 表示。

式中:Tg,max(t) 表示t时刻卫星姿态机动最大需求时间,ag,max(t) 为卫星任务需要的最大姿态转角,vg为姿态机动转速,c为卫星姿态稳定时间。

②固存接受的最大拍摄时间

在固存容量方面, 观测卫星的存储上限不仅受限于卫星单次服务时间, 同时依赖于卫星何时对固存进行格式化擦除。 如公式(12) 所示, 固存接受的最大拍摄时间:

式中:Tf_s,max(t) 表示t时刻固存所能接受的最大拍摄时长,Δs(t) 为t时刻观测卫星剩下的存储容量,vw,min为星上固存允许的最小写入速度。

③能量允许的最大拍摄时长

在电量方面, 观测卫星对日充能的时刻与时间也制约着卫星的拍摄时长,t时刻能量允许的最大拍摄时长表示为Te_s,max(t) 。

4 基于时间约束的天基观测补网规划建模与求解

4.1 多时间约束的补网规划模型

结合第二节中卫星观测时间分析, 本文以如下符号描述天基观测补网规划问题中的参数:①TiL: 卫星si空闲时间窗口集合; ②TijP: 卫星si对目标aj的可见时间窗口集合; ③Tk ijExe: 卫星si对目标aj的第k个可执行时间窗口; ④Tig,max:卫星si姿态机动最大时长; ⑤Tif_s,max: 卫星si固存接受的最大拍摄时长; ⑥Tie_s,max: 卫星si储能允许的最大拍摄时长; ⑦TjDeadline: 目标aj的任务截止时间; ⑧TjObs目标aj任务要求观测时长。一个多时间约束的天基观测补网规划问题可以用5 元组表示, 其中:

A: 观测任务集合,A={a1,a2…,an} ,n表示需要规划的元任务数量。

S: 卫星资源集合,S ={s1,s2…,sm} ,m表示参与补网的卫星资源数量。

TE: 可执行时间窗口集合, 即为的集合,i≤m,j≤n,k取值范围由实际计算得到,为可执行开始时间,为可执行结束时间, 这里的时间窗口与任务目标和卫星资源有对应关系。

: 原任务规划变量集,表示原方案中事件“目标aj由卫星si在范围进行观测” 被规划,表示未被规划。

Z: 新任务规划变量集,表示新方案中事件“目标aj由卫星si在范围进行观测” 被规划,表示未被规划。

根据以上约定, 我们建立补网规划问题的约束条件:

条件(1) 表示卫星观测时间满足可用且可见; 条件(2) 表示观测时间满足卫星工况约束;条件(3) 表示观测时间满足任务时间要求; 条件(4) 防止资源冲突, 即同一卫星资源时间窗口, 不能同时分配给两个及两个以上的任务, 且同一卫星的两任务执行上至少需要保留姿态转换的时间间隔; 条件(5) 防止资源冗余, 即某一任务一旦已经执行, 原则上不再安排其他时间或其他卫星资源再执行。

在此基础上, 目标函数构造如下:

(3 ) 最小化任务结束时间:

利用信息熵加权法合成三个子目标, 设置α,β,γ为影响因子。 根据天基观测补网的特点,约定α≥β≥γ。 最终优化目标:

当优化结果F ＜α时, 判断观测补网规划失败,决策者需要精简任务或增加资源; 当α≤F≤α +β时, 判断补网规划成功, 但原规划方案有调整;当F ＞α+β时, 判断补网规划成功, 原规划方案无需调整, 新任务和资源直接插入原规划方案即可。

4.2 算法设计与求解实现

相关研究表明, 卫星观测任务规划问题是一类典型的NP-hard 问题, 难以求解, 且问题的组合爆炸特征十分明显。 现代智能优化算法在求解组合优化问题方面显示了较强的能力, 但由于本文模型时间约束条件较多, 势必导致计算速度缓慢, 影响下一步的规划部署, 不适合动态应急补网。 基于规则的启发式算法可以综合考虑优先规则, 并加入一定的随机因素, 从而获得满意的结果, 其优势在于运行速度较快, 但难以从全局优化的角度搜索问题解。 笔者通过选择吱呀轮算法(Squesky-Wheel Optimization, SWO) 作为导向式搜索, 快速获取可行解, 再利用遗传算法(Genetic algorithm, GA) 充分扩展可行解的搜索空间, 通过这两种算法整合预提高模型求解效率和求解质量。 算法具体步骤如下。

(1) 编码方法

借用文献[11] 中编码思想。 将天基观测规划问题每个解划分两个部分: 一是对卫星资源分配序列(Satellites Assignment, SA), 将每个元任务分配给一颗观测卫星; 二是针对元任务每卫星资源可执行时间分配序列 (Time Assignment,TA), 即为每个元任务和对应的卫星资源分配执行开始时间和结束时间。 基因的编码采用自然数编码, 每个基因的序号对应元任务按截止时间由小到大排序的序号, 基因座上的基因值标识是卫星与执行时间的编号, 参见图1。

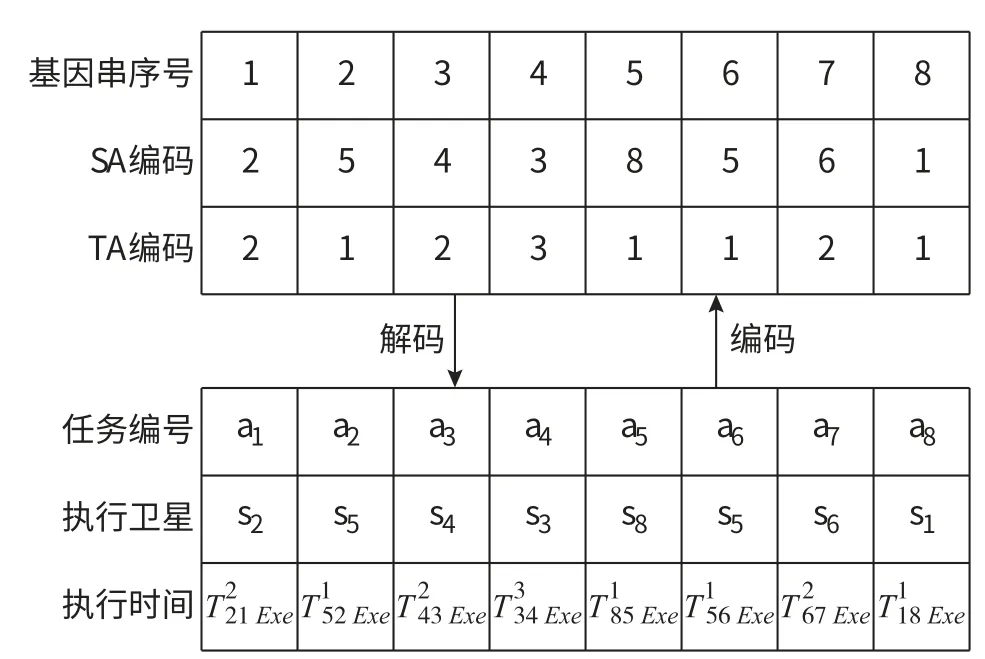
图1 算法编码Fig.1 Algorithmic coding

(2) 初始化种群

初始种群的产生速度和质量影响算法的运行效率, 快速生成高质量初始种群是我们算法的关键步骤。 我们引入SWO 算法快速获取多样性的初始解。 SWO 算子由构造器、 分析器和排序器组成, 如图2 所示。

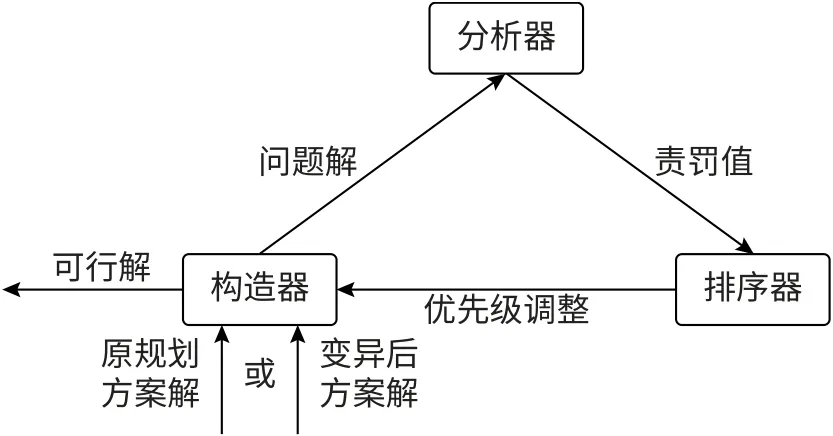
图2 SWO 算子迭代过程示意图Fig.2 SWO operator iteration process diagram

①构造器设计

对照原规划方案从已排序的任务但未安排资源的序列中依次选出可供使用的各个执行卫星和对应时间, 将其插入到已安排任务序列中, 如果没有已安排任务与当前任务冲突, 则插入成功,跳过分析器和排序器, 生成一基因串。 否则将计算当前任务和与之冲突的已安排资源任务一起转入未安排任务重新规划, 进入分析器和排序器进行局部优化搜索排序, 再回到构造器重新生成规划结果。

②分析器设计

分析器主要是对个体内部进行编排梳理。 为了加快搜索速度, 防止一个资源在迭代过程中被反复地安排、 取消、 再安排, 分析器采用最小冲突原则进行责罚值Penalty 分析。

式中:fi为迭代过程中资源i在被安排及取消的次数,l为迭代次数,δ∈(0.5, 1) 为机会因子。

③排序器设计

排序器按资源的责罚值由大到小顺序对未安排任务序列排序。

(3) 个体适应度值

将规划模型的目标函数作为该算法的适应度函数。 但是由于本文采用的天基补网任务规划模型是多目标的约束满足模型, 最终的适应度值采取熵权法为各目标函数赋权计算所得, 即根据种群内部个体的三个目标函数值, 进行计算信息熵, 并根据信息熵的数值明确各目标的权重, 最后使用该权重计算目标函数值的和作为该个体的适应度。

(4) 选择操作

以个体适应度占种群适应度的比例为选择概率, 对群内部每个个体选择操作。 对种群内部所有个体按其概率选取两个个体。

(5) 交叉操作

对于选择出的父代按照交叉概率p并随机选择基因执行交叉操作, 生成两个子代个体。

(6) 变异操作

对种群中所有个体运用变异算子之前采取精英保留策略, 即种群内部表现优秀的个体不会触发变异, 精英保留比例为10%～25%之间。 针对其他个体中每个SA 编码以变异概率q进行变异操作。

(7) 新第一代种群

对交叉后的新个体进行可行解获取, 如图2所示, 处理过程同获得初始种群方式保持一致。利用信息熵加权法更新新种群内所有个体的适用度值。

(8) 终止条件判断

若达到最大迭代次数或种群中最大适应度值满足要求, 则终止运算, 否则转入步骤4 选择操作进行新一轮迭代。

5 仿真实验与分析

仿真场景设定原规划中15 颗低轨卫星选自STK 软件中的卫星数据库, 200 个空间目标选自Spare-Track 网站下载的TLE 数据, 并借助STK 软件与Matlab 软件计算可执行时间窗口。 任务观测截止时间按24h 至48h 随机生成, 任务未全部完成, 需启用补网规划。

本实验中设置补网中增加10 颗对地遥感卫星,遗传算法中交叉概率p= 0.7, 变异概率q= 0.05。将天基观测补网最终优化目标进行归一化处理,令Vd= F/(α + β + γ) , 并取多目标加权因子α= 100,β=10,γ=1。 图3、 图4 和图5 分别展示了不同观测目标数量变化情况下算法运行1000次的平均寻优结果、 平均计算时间和方差稳定性的比较。

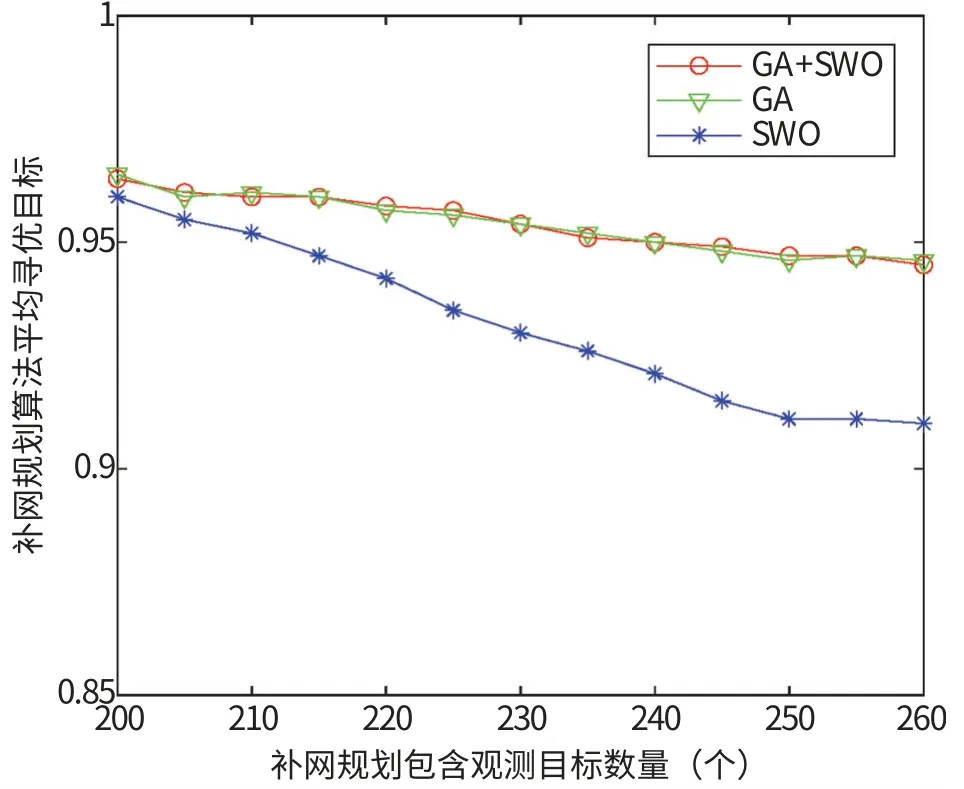
图3 不同观测目标数量变化情况下三种算法的平均寻优目标比较Fig.3 Comparison of the average optimization target of three algorithms under the condition of different number of observation targets

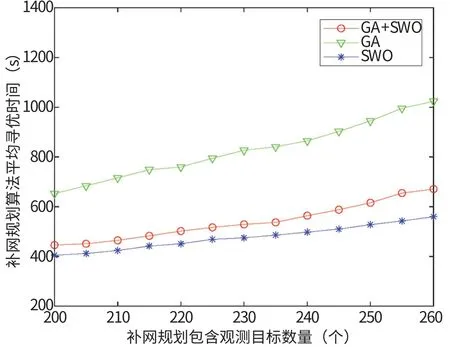
图4 不同观测目标数量变化情况下三种算法的平均寻优时间比较Fig.4 Comparison of the average optimization time of three algorithms under the condition of different number of observation targets

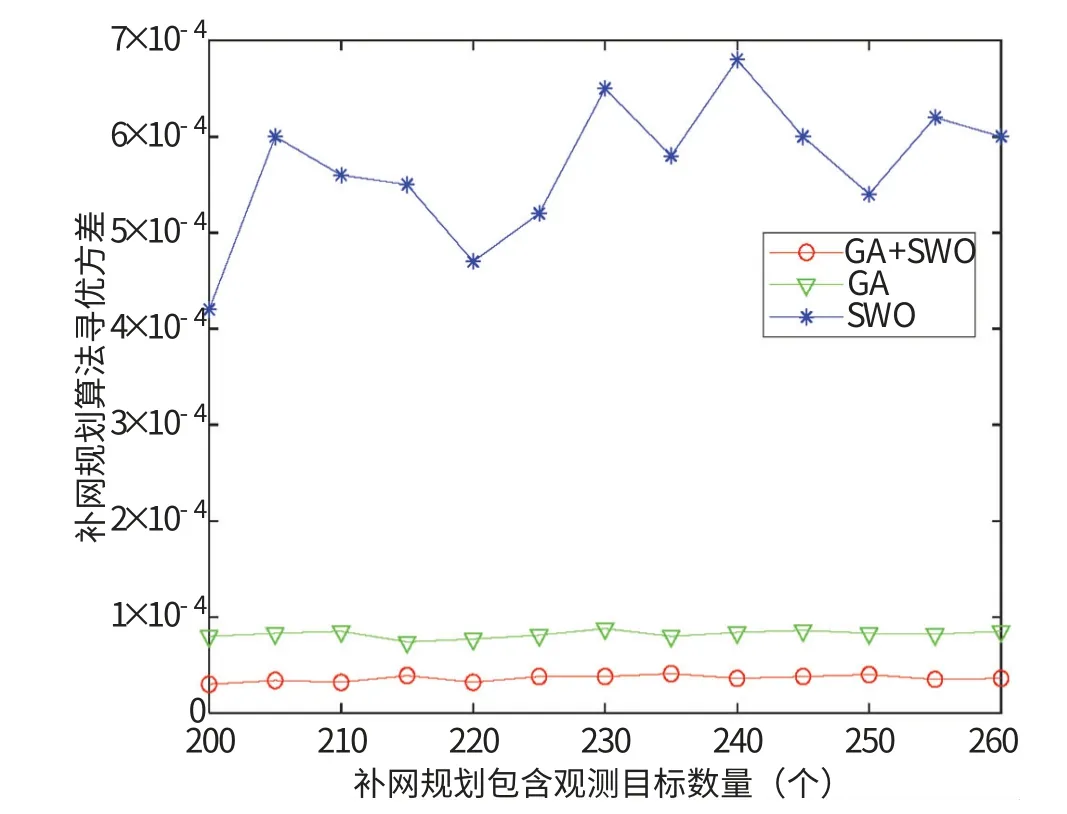
图5 不同观测目标数量变化情况下三种算法的寻优稳定性比较Fig.5 Comparison of the average optimization stability of three algorithms under the condition of different number of observation targets

在增加卫星资源的情况下, 如图3 所示, 三种算法的寻优目标值都大于0.9, 即任务完成率达到100%。 图3 表明随着观测目标增加三种算法的寻优目标值虽大于0.9 但都有所下降。 这说明在增加一定补网资源数量的情况下, 随着任务数量递增, 即使任务成功率能达到, 但原方案变动率和任务最早结束时间却随之变差。

图3 中GA 算法曲线明显高于SWO 算法曲线, 表明针对本文规划问题GA 算法在寻优目标性能上优于SWO 算法, 改进后GA 算法与GA 算法曲线接近。 图4 表明针对本文规划问题SWO 算法具有最佳的寻优时间性能, GA 和SWO 组合算法在寻优时间性能上胜过GA 算法。 图5 由各算法运行1000 次实验统计获得方差分析三种算法稳定性差异, 表明GA 和SWO 组合算法求得的最佳解相比其他两种方法较为稳定。 综上所述, GA和SWO 组合算法与GA 算法在寻优目标值上无显著差异, 但在寻优时间和寻优稳定性上有较大提升。

6 结论

针对在资源不足情况下天基观测规划问题,本文主要完成三项工作: (1) 分析天基观测补网规划的需求和特点, 确定补网规划的任务目标;(2) 考虑对地遥感卫星的空闲窗口, 明确卫星资源可执行观测任务的时间约束; (3) 鉴于多条件约束需要满足, 建立基于时间约束的补网规划模型, 并进一步采用遗传算法和吱呀轮的组合算法进行求解。 利用STK 提供仿真数据进行实验分析, 验证了模型的有效性, 实验表明遗传与吱呀轮的组合算法在求解方案的评价、 算法收敛速度和稳定性方面都表现出较高的性能。 该研究不仅可以为今后空闲卫星加入天基观测补网提供参考, 更可以为实现天基观测动态调度的重用性和稳定性提供有力支持。