第34届北京市高中力学竞赛预赛压轴试题的5种求解方法

娄员俊 方林 许新胜

(1.阜阳市临泉县临泉田家炳实验中学 2.合肥市巢湖市第四中学3.安徽师范大学物理与电子信息学院 )

本文以第34届北京市高中力学竞赛预赛的压轴题为例,运用5种方法分析试题第(2)问,以期拓展学生的科学思维,提升其创新能力.

原题物理小组研究小车转弯的情况,在弯道半径为R的水平路面上.车辆转弯时发生了横向滑动的现象.

(1)试分析小车发生横向滑动的原因.

(2)他们设计了一个解决滑动的办法:将弯道路面的外侧抬高,使弯道路面的横断面如图1 所示,路面与水平方向倾斜角度为α,若车轮胎与路面间横向的最大静摩擦力等于它对路面压力的μ倍,要使小车通过这个半径为R的弯道不发生横向滑动,试分析讨论它行驶的速度可能为多少?

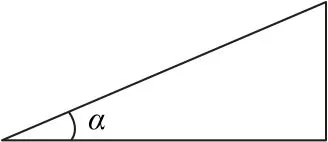
图1

分析(1)小车在水平路面上转弯时,相当于在水平弯道上做圆周运动.当小车速度过大,以至于横向最大静摩擦力不能提供其做圆周运动的向心力时,便会发生横向滑动.

点评

该题情境为小车转弯问题,需要考生在建构质点做匀速圆周运动模型的基础上,结合临界状态的受力与运动进行分析,解决问题的关键在于根据向心力公式求出转弯时的最大速度和最小速度.试题源于教材又未拘泥于教材,学生并不陌生,但设问具有开放性,且运算量较大,可对学生模型建构、推理论证等能力进行有效甄别.

(2)方法1 分解力

设当小车的行驶速度为v时,它恰好不受斜面的横向静摩擦力,此时小车受重力mg和垂直斜面向上的支持力FN.由牛顿第二定律得车与路面间无摩擦力时,支持力的水平分力提供向心力,如图2-甲所示,根据向心力公式得FNcosα＝mg,FNsinα＝,解得

若小车行驶速度v＜v0,则车轮受到的横向静摩擦力Ff方向沿斜面向上,且速度v越小,Ff越大,当Ff达到最大值Ffm时,速度即为不发生横向滑动的最小速度vmin,此时小车的受力示意图如图2-乙所示.

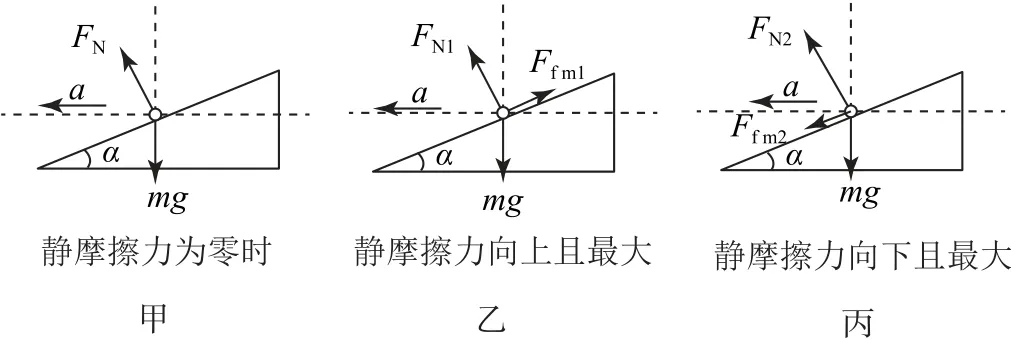
图2

由牛顿第二定律得,当小车在路面上不做侧向滑动,且沿斜面向上获得最大静摩擦力时,有

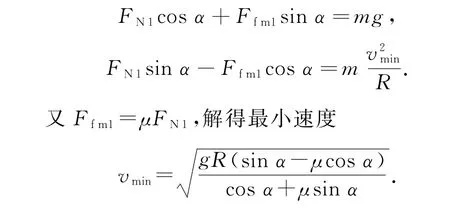
若小车行驶速度v＞v0,则车轮受到的横向静摩擦力Ff方向沿斜面向下,且速度v越大,Ff越大,当Ff达到最大值Ffm时,速度即为不发生侧向滑动的最大速度vmax,这时小车的受力示意图如图2-丙所示.由牛顿第二定律得,小车在路面上不做侧向滑动,且沿斜面向下获得最大静摩擦力时,有

方法2 分解加速度

当小车拐弯时,将加速度沿斜面和垂直斜面方向进行分解,如图3 所示,则

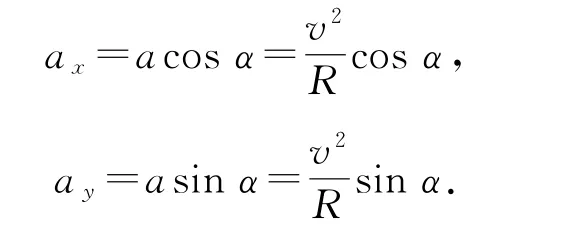
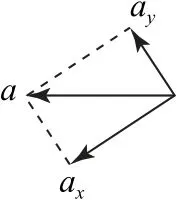
图3

当拐弯速度最小时,车轮受到的横向静摩擦力Ff方向沿斜面向上,对图2-乙情境,根据牛顿第二定律有,平行斜面方向

当拐弯速度最大时,车轮受到的横向静摩擦力Ff方向沿斜面向下,对图2-丙情境,根据牛顿第二定律有,平行斜面方向

方法3 力的合成矢量图

将小车拐弯的情境抽象为质点做匀速圆周运动模型,则汽车受重力、支持力、摩擦力的合力恰好指向圆心,充当向心力.根据矢量合成方法,三种情形相应的受力及合力图如图4、5、6所示.

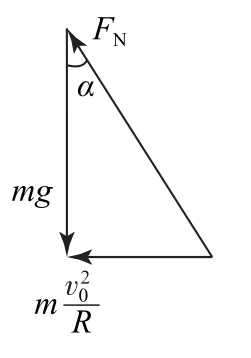
图4

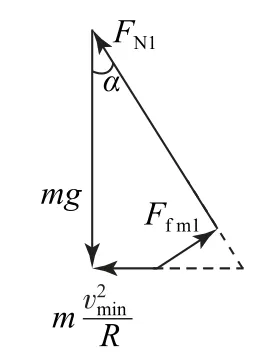
图5

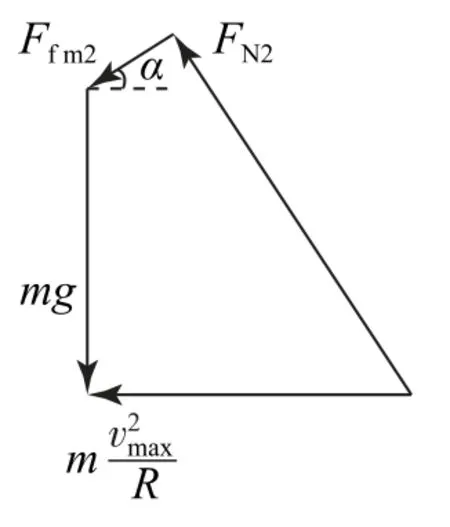
图6

对图5情况,竖直方向有

方法4 惯性离心力法

小车转弯过程,引入惯性离心力ma*＝,方向沿半径方向向外,则汽车始终处于平衡状态,以图2-乙情境为例作出受力分析图如图7所示,依次根据水平方向和竖直方向的平衡条件有

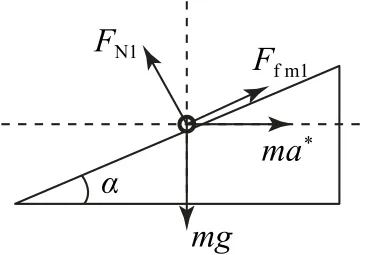
图7

讨论下面对图2 中甲、乙、丙三种情况进行讨论.

图2-甲所示情况,此时静摩擦力为零,这时的速度是汽车拐弯时刚好受或不受静摩擦力状态的临界速度.

图2-乙所示情况,若sinα－μcosα＝0,即μ＝tanα时,则vmin＝0,即无论小车以多小的速度转弯,都不会相对斜面向下滑动;若sinα－μcosα＜0,即μ＞tanα时,求解最小速度的式子无意义,因为这种情况下,最大静摩擦力与惯性离心力沿斜面向上分力的合力大于重力沿斜面的分力,小车沿斜面方向无法平衡,故无论行驶速度是多小,轮胎受到的沿斜面向上的静摩擦力都不可能达到最大值.

图2-丙所示情况,若cosα－μsinα→0,即μ→,此时vmax→＋∞,即小车无论以多大速度行驶,都不会相对斜面向上滑动;若cosα－μsinα＜0,即,求解最大速度的式子没有意义,因为这种情况下,重力与惯性离心力沿斜面向下分力的合力大于最大静摩擦力,小车沿斜面方向无法平衡,故无论行驶速度是多大,轮胎受到的沿斜面向下的静摩擦力都不可能达到最大值.

还可以从向心力方向的角度来分析以上两种无意义的情况.

对图2-乙所示情况,假设小车有横向下滑趋势,此时小车受力如图8所示.若sinα－μcosα＜0(即μ＞tanα),则支持力与最大静摩擦力的合力方向偏向图中右上方,所有力的合力不可能刚好完全提供水平向左的向心力.

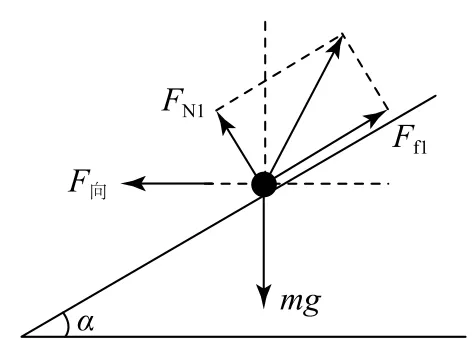
图8

对图2-丙所示情况,假设小车有横向上滑趋势,此时小车受力如图9所示.若cosα－μsinα＜0,即,则支持力和摩擦力的合力偏向图中左下方,所有力的合力不可能刚好完全提供水平向左的向心力.

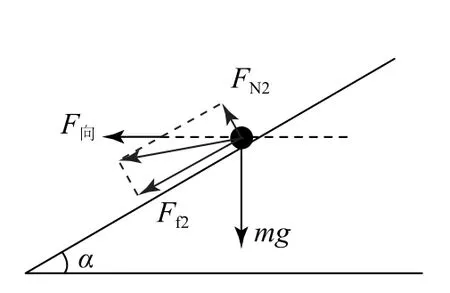
图9

方法5 分析法

小车在倾斜路面的弯道上受重力mg、支持力FN和静摩擦力Ff,Ff的正方向设为沿斜面向上,如图10所示.沿水平方向和竖直方向的分量方程分别为

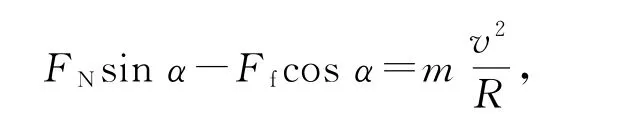
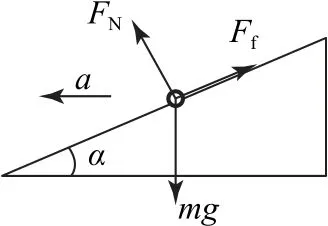
图10

上式中若sinα－μcosα＝0,则vmin＝0,若sinα－μcosα＜0,上式无意义,但总有ΔFf＞0,即无论以多小的速度拐弯,小车都不发生横向滑动.

如速度由v逐渐增大,静摩擦力Ff＜0,即方向沿斜面向下,随着v的继续增大,Ff的大小逐渐增大,直至(cosα－μsinα)＝0时,速度为最大,即

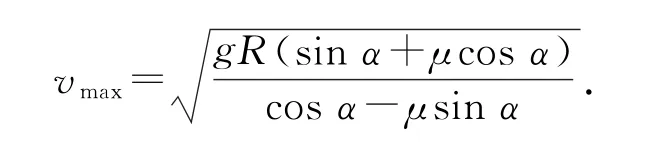
上式中若cosα－μsinα→0,此时vmax→＋∞,即汽车的最大速度没有限制;若cosα－μsinα＜0,此式无意义,而总有＞0,即汽车无论以多大速度行驶,都不会沿斜面向上滑动.

(完)