动态灾害环境下多对多物资配送路径规划方法

胡小兵，孟相至

1.中国民航大学 电子信息与自动化学院，天津 300300

2.中国民航大学 中欧航空工程师学院，天津 300300

我国是世界上因自然灾害死亡人数最多、经济损失最严重的国家之一[1]，灾害救援在保障人民群众的人身和财产安全中起着举足轻重的作用，而物资配送又是其中的重要一环。传统的物资配送规划方法经常根据就近配送的原则采取固定路径的静态预案规划（static plan optimization，SPO）。SPO方法按应急物资储备点就近配送的路径规划原则看似有效，实则没有考虑应急物资储备点周边路网环境受动态灾害影响的情况。考虑到台风、洪水、火灾等灾害的动态发展变化对路网环境的通达性会产生影响，固定的路径规划通常不能很好地满足实际要求。因此需要打破物资储备点服务范围的限制、采取灵活的配送方法，这就要利用动态路径优化（dynamic path optimization，DPO）方法。同时，由于涉及到多个应急物资储备中心的物资调度以便及时救援多地受灾群众，这就需要在动态环境下进行多对多的路径优化。动态环境下的多对多路径规划问题在灾害救援、交通运输等领域有较强的应用潜力，迫切需要解决。该问题需要在路径搜索过程中应对路网环境随时间的变化，并找到不同应急物资储备点、配送点之间的最佳对应关系以保证结果的最优性，同时保证动态路网环境下求解的时效性和成功率。

现阶段应用于动态路径优化问题的搜索算法主要分为三种：确定性算法、进化算法和势场算法。确定性算法包括A*算法[2-3]和Dijkstra算法[4-5]等，进化算法包括粒子群优化算法[6]、遗传算法[7]和蚁群算法[8]等，势场算法包括向量场法[9]和人工势场法[10]等。其中A*算法和Dijkstra算法因具有确定性和最优性以及良好的可扩展性而得到广泛应用[11]。但总体来说，现有算法无法通过一次计算得到动态环境下多对多路径优化问题的理论最优解。基于上述算法的传统DPO方法的求解思路是：基于当前时刻的路网环境，利用一对一问题的迭代求解来解决动态路网环境下多对多路径优化问题[12-13]。然而这存在如下弊端：首先，面对复杂问题会极大降低计算效率；其次，单次迭代中起点终点需要事先指定并一一对应，因此无法根据动态环境实时调整，一旦某一个起点或其周边路网因灾情陷入困境必然会导致该点对应的所有路径规划的失败；最后，在单次迭代计算中一旦某一条路径规划陷入困境会影响后续相关步骤的执行。从另一个角度看，DPO方法大多是针对当前时刻路网情况的静态路径优化过程[14]，当路网变化时要重新进行路径优化。这不但导致路径优化效率低下，同时，针对灾害环境下的动态路网问题存在绕路或折返的可能性，容易导致实际走过的路径与理论最优路径不一致。如图1所示，由于灾害障碍区的动态变化导致传统DPO方法下的实际运动路径偏离理论最优路径。

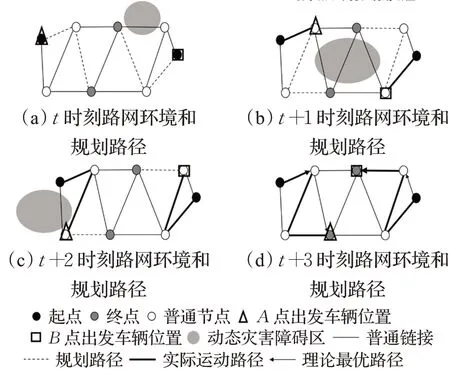
图1 传统DPO方法的弊端Fig.1 Disadvantages of traditional DPO methods

为了更好地解决动态灾害环境下的多对多路径优化问题，本文将改进拓展基于涟漪扩散算法（ripple spreading algorithm，RSA）的协同进化路径优化（coevolutionary path optimization，CEPO）方法。该方法从理论层面为解决上述问题提出了一种新的解决思路，它不仅具有良好的计算时效性，并且可以化解传统方法求解动态环境下多对多问题灵活性差、绕路甚至求解失败的风险。因此，本文提出利用CEPO方法解决上述问题，并利用仿真实验与其他方法进行对比研究。

1 动态灾害环境下多对多物资配送数学模型

1.1 问题描述

假设在路网中存在着多个应急物资储备点和多个物资配送点（即，受灾居民点），在灾害影响范围动态变化过程（例如，台风移动、洪水泛滥）中力求以最短的时间将应急物资运送到所有配送点。通常情况下，物资配送点的数量大于物资储备点的数量，因此同一个物资储备点可能会有多部车辆出发前往多个物资配送点。事实上，由于路网受动态灾害的影响，可能会导致某个物资储备点无法向某些物资配送点运送应急物资，甚至无法向外运送出任何物资。因此，某一物资储备点应该向哪些物资配送点派出车辆在动态灾害环境下通常是难以预先知道的。

然而，传统的物资配送采取SPO方法。静态预案通常没有也难以考虑灾害的动态影响，而是一味追求物资储备点和配送点的实际最短路径，即：静态预案采取静态路网环境下的固定规划路径，人为地固定起点终点的对应关系并为物资储备点划分配送范围。因此，它无法适应灾害环境的变化进行动态路径规划，同时由于配送范围的限制而无法得到动态灾害情景下的全局最优路径。如图2所示的路网环境中，由于受到灾害动态障碍区的影响，A号物资储备点按照静态预案规划的路径无法实现物资配送的功能，这在现实情况中是普遍存在的。

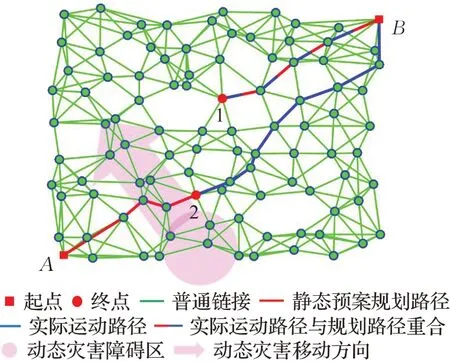
图2 物资配送案例Fig.2 Material distribution case

与此同时，学者们尝试利用DPO方法解决SPO方法无法适应路网变化的问题。DPO方法同样采取固定起点终点对的路径规划方式，但与SPO方法不同的是，DPO方法在路径规划的同时实时更新路网环境，当路网更新后以当前位置为起点重新进行路径规划。因此DPO方法的本质为静态路径规划的在线迭代计算。这不但降低了计算结果的优越性和时效性，同时对计算能力有较高的要求。

针对SPO方法和DPO方法的诸多弊端，这就需要新的路径规划方法能够根据灾害环境的变化动态调整规划路径，同时主动打破僵化的起点终点对应关系，以得到动态灾害情景下的全局最优路径。除此之外，新的路径规划方法还需要高效完成多起点多终点的路径规划，因为在现实的物资配送问题中，经常需要同时从数十个物资储备点向成百上千个受灾居民点配送应急救援物资。

针对上述问题，本文基于SPO方法将其转化为求解如下数学问题：

其中，Pit0*为SPO方法根据初始时刻t0的路网环境E(t0)计算出第i个起点终点对的最优路径，ND为终点数（即，受灾居民点的数目）。与之相比，DPO方法的数学描述为：

1.2 CEPO方法数学模型

CEPO方法通过植入动态灾害模型将路径搜索过程与灾害扩展过程相结合，实现一次离线搜索得到多对多问题的理论最优路径，有效保证了结果的优越性和时效性，这与SPO方法和DPO方法有着本质不同。CEPO方法将动态灾害环境下的多对多路径优化问题描述为求解下列数学问题：

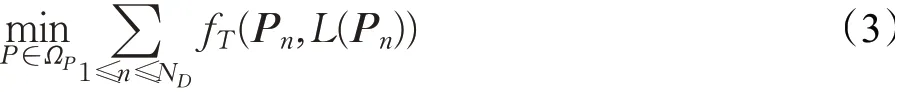
并且满足：

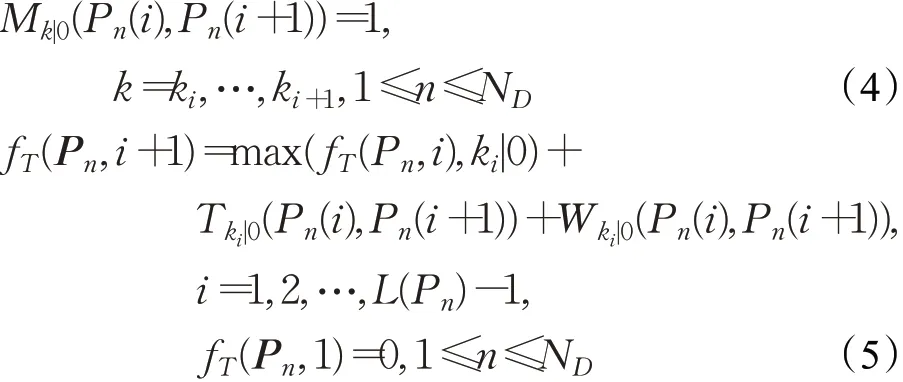
其中，P n是一个向量，记录了路网中连接第n个起点终点对路径上的所有节点，L(P n)给出了路径P n上节点的总数，例如Pn(1)是路径P n的起点，而Pn(L(P n))是路径P n的终点。fT(P,i)是计算沿路径P通行并到达第i个节点时所耗时间的函数，ΩP为连接起点和终点所有可能路径的集合，ND为终点的数量（即，在多对多问题中最多需要找出ND条最优路径）。由公式（3）可知，CEPO方法将上述问题转化为求解最短耗时路径的问题。与此同时，P(i)代表路径P的第i个节点，ki是沿路径P到达节点P(i)的预计可达时间。M k|0(Pn(i),Pn(i+1))=1意味着根据t=0时刻的预测，节点Pn(i)与Pn(i+1)在未来时刻k直接相连。这是因为在动态灾害环境下，路网通达性随时变化，因此公式（4）保证了节点Pn(i)与Pn(i+1)在k时刻的通达性。同样地，T k|0(Pn(i),Pn(i+1))表示根据t=0时刻的预测，通过节点Pn(i)与Pn(i+1)在时刻k的链接所需要的通行时间，Wk|0(Pn(i),Pn(i+1))表示根据t=0时刻的预测，在节点Pn(i)与Pn(i+1)的时刻k的链接上所需要的等待时间。因此，公式（5）给出了沿路径Pn到达第i+1个节点的时间，它由到达第i个节点的时间、从第i到第i+1个节点的通行时间以及等待时间组成。M k|0、Tk|0和W k|0在k|0时刻的预测值与路网的动态变化有关，可以表示为：

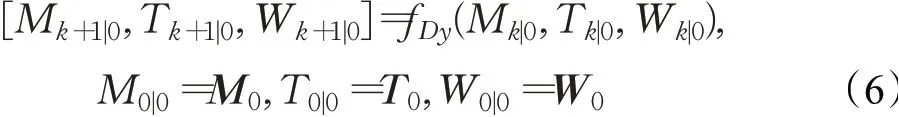
其中，f Dy为路网的动态变化函数，M0、T0和W0是t=0时刻的路网通达性矩阵、通行时耗矩阵和等待时耗矩阵。

基于公式（3）、（5）和（6），当给定路网的动态变化函数f Dy，以及t=0时刻的初值M0、T0和W0后，希望可以通过一次性的离线计算得到动态灾害环境下多对多问题的最优路径。这相比于DPO方法采取循环迭代的计算方式将具有明显的优势。

2 CEPO方法基本原理及改进设计

2.1 CEPO方法基本原理

CEPO方法是在给定的动态灾害环境下，仅通过一次路径优化，使原始尺寸的路网随同面向时间单位的优化步骤共同进化，以得到动态灾害环境下的理论最优路径。CEPO方法是离线路径优化方法，其核心算法是RSA算法。RSA是受自然界涟漪扩散现象启发而提出的一种多主体、自组织仿真模型[15]，通过在特定问题的路网中进行涟漪扩散接力赛完成搜索过程。并且，RSA只需要定义单个节点的涟漪产生、扩散和消失行为，一旦某一个涟漪到达终点就立即停止涟漪扩散接力赛过程，然后通过回溯涟漪所走过的路径即可得到最优路径。也就是说，CEPO方法将涟漪扩散过程与面向仿真时间单位的路网变化过程相结合，当不同涟漪相互竞争时，涟漪所经过的路网会同时动态地变化。首先，起点激发初始涟漪，当涟漪扩散到相邻节点，则在该节点激发新的涟漪。其次，一旦与某一涟漪中心节点相连的所有节点全部被激发，则将该节点锁定，这意味着该节点无法再激发新涟漪。在动态灾害环境下，随着障碍区的移动路网的通达性随之改变，如果与某个节点相连的链接不可通达（即：呈锁定状态），则将该节点上新激发的涟漪设为等待状态，这意味着该节点将在链接可以通达时才扩散新的涟漪。最后，从最先到达终点的涟漪回溯即可得到动态灾害环境下的理论最优路径。因此，最终到达终点的涟漪会在其扩散期间恰当地避开所有临时不可到达的节点和链路，这也就为动态灾害环境下实现路径优化提供了理论保证。

2.2 动态环境下多对多路径规划传统方法

针对动态灾害环境下的多对多路径优化问题，目前已有多种解决方法。为了解决SPO方法面对动态灾害变化容易导致规划路径应用失败的弊端，在现实应用中引入了等待行为进行改进，即运输车辆在行驶过程中遇到因灾情变化导致路网不通时便原地等待，等灾情过境继续按既定路线行驶至终点。然而，改进后的SPO方法在等待过程中浪费了宝贵的物资配送时间。因此，学者们又提出了DPO方法，该方法实时监控灾情变化并计算当前位置和时刻到终点的最优路径以规避灾情的影响。由于DPO方法采取一对一迭代的计算方式，因此它并没有从根本上打破配送范围的限制。得益于计算机技术的发展，学者们通过对DPO方法的改进利用遍历所有起点终点组合的计算方式（即，求解起点终点的所有可能对应关系，从中找到全局最优路径）以打破配送范围的限制。但是，改进后的DPO方法仍然有着诸多弊端。首先，改进后的DPO方法本质仍是静态路径优化方法，需要每隔一定时间根据当前路网环境重新计算，并遍历所有起点终点的可能组合以得到当前时刻的最优路径。显然，该方法面对复杂问题时对计算能力有极大的要求，这势必会降低计算的时效性。除此之外，改进后的DPO方法局限于计算基于当前时刻路网环境的最优路径，在理论上，其结果最优性会随时间推移而丧失。

2.3 将CEPO方法拓展到多对多问题

针对传统方法的诸多弊端，文献[14]提出的CEPO方法通过引入动态环境预测模型，实现了运动路径优化与动态灾害环境的协同进行，通过一次离线计算得到理论最优路径。这不仅极大降低了计算量、保证了结果的实时性，同时在初始时刻考虑了灾情的演化全过程，保证了计算结果的理论最优性。不过，文献[14]提出的基于RSA的CEPO方法只能解决动态路网环境下的一对一优化问题（即，只有一个起点和一个终点的问题）。本文对其进行了必要的改进以扩展到动态灾害环境下的多对多优化问题，以便有效应对多个物资储备点和多个受灾居民点的情况。

本文对RSA主要做了下面两个重要的改进。文献[14]提到的RSA算法中，由第一个到达节点的涟漪激发出新的涟漪，且每个节点最多被激发产生一个新涟漪。这个规则只能满足求解一对一优化问题的需要，要想求解多对多优化问题，就必须改变每个节点最多只能被激发产生一个新涟漪的规则。假设共有NS个起点，本文将对RSA做如下修改：每个节点最多可以被激发产生NS个新涟漪，并且一个节点处所激发出的NS个新涟漪需满足如下条件：不存在激发源头为同一个起点的多个新涟漪，即，任何一个起点为源头在该节点处最多激发出一个新涟漪。其次，本文对涟漪扩散的终止条件也进行了修改。文献[14]在求解一对一优化问题时，一旦有一个涟漪到达终点，涟漪扩散接力赛立即停止。为了求解多对多问题，本文修改如下：如果存在至少一个终点还没有任何一个涟漪到达，那么涟漪扩散接力赛就需要继续进行。

改进后的RSA的算法流程图如图3所示。图中SR(r)表示涟漪r的状态，SR(r)=0/1/2表示涟漪分别呈不活跃、等待、活跃状态。其中，E(r)表示涟漪r的中心节点，R(r)表示涟漪r的半径，T(r)表示哪个涟漪激发产生了涟漪r。t=0在涟漪扩散中，A(z|0)(i|j)表示根据在时刻做的预测节点i和节点j会在z时刻直接相连，C(k,z|0)(i,j)表示在z时刻节点i和j之间的第k个长度，Nn表示节点i激发产生涟漪的数量。由图3可知：首先，在多对多问题中存在多个起点和终点，因此，步骤1初始化设置了NS个初始涟漪，并且步骤2中只有当所有终点都有涟漪到达后结束循环。其次，步骤3.1至3.3表示对路网、时间参数以及包括终点在内的任意节点涟漪状态进行更新。步骤3.4至3.6表示对节点n激发涟漪的数量进行更新，若大于起点数量NS则更新路网，使得节点n永久不可通达并且不再激发新涟漪。步骤3.7引入等待行为来解决在动态灾害环境下节点的暂时不可通达问题，步骤3.8表示利用涟漪扩散速度对涟漪半径的更新。由步骤3.6可知当节点n产生的一个涟漪到达与之相连的所有节点后，则该涟漪消亡。最后，从最先到达终点的涟漪回溯即可得到动态灾害环境下的多对多问题的理论最优路径。图4示例了基于RSA的CEPO方法如何通过涟漪接力赛找到动态灾害环境下多对多问题的最优解。由图4可见，根据静态预案一般会安排起点1救援节点6，而起点12救援节点7，但是在图4示例的动态灾害环境下的理论最优救援方案恰恰相反，即，应该由起点12救援节点6，而起点1救援节点7。图4中的涟漪扩散接力赛与路网的动态变化同步进行，因此基于RSA的CEPO方法通过仅仅一次（即，不需要重复迭代运行多次）涟漪扩散接力赛就成功地找出了所有起点终点之间的理论最优对应关系和相应的理论最优路径。

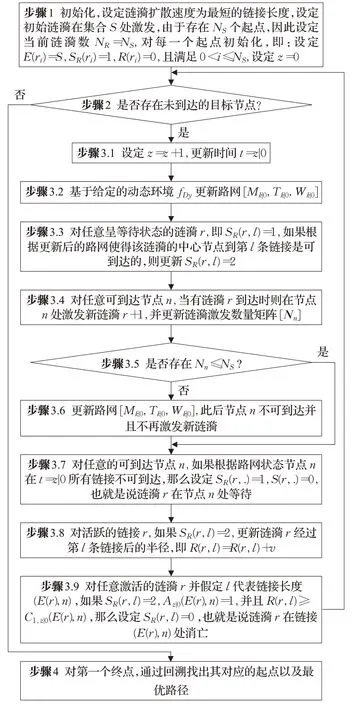
图3 多对多动态灾害环境下的RSA流程图Fig.3 RSA flow chart in many-to-many dynamic environment

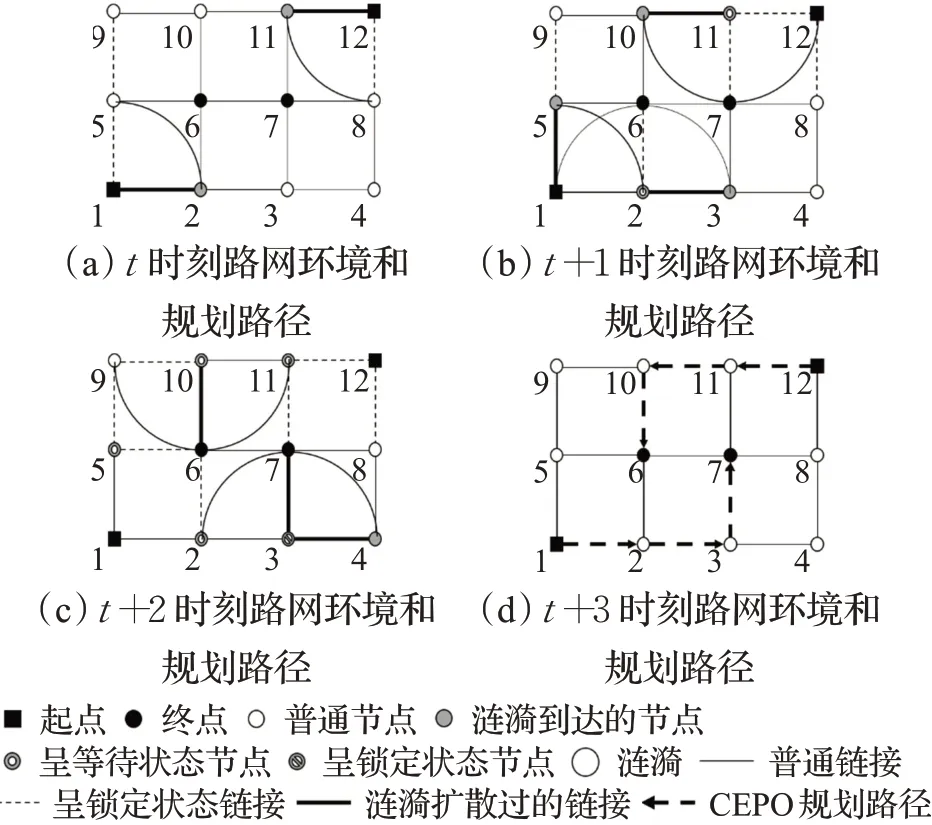
图4 基于RSA的CEPO的涟漪接力赛Fig.4 Ripple relay race based on RSA-based CEPO method

3 理论分析

3.1 算法最优性分析

对于RSA算法的最优性，本文得出如下定理：

定理1对于给定的动态灾害环境，在多对多RSA的涟漪扩散接力赛中，首先到达终点的涟漪所经过的路径为动态灾害环境下的理论最优路径。

证明涟漪扩散这一自然现象中反映的优化原理保证了RSA在路径优化中的最优性，该原理指出：涟漪在各个方向上以相同的速度扩散，因此总是先到达最近的空间点。文献[15]给出了RSA解决静态路网环境问题最优性的证明，虽然在动态灾害环境下存在移动障碍区域，但是该证明同样适用。因为障碍区域仅改变了节点或链接的通达性，而这对所有涟漪是一视同仁的，同时，在竞赛中涟漪可以选择在障碍前等待或绕开障碍。因此，首先到达终点的涟漪所经过的路径为动态灾害环境下的理论最优路径。

3.2 算法复杂度分析

基于RSA和CEPO的基本原理，本文得出以下定理：

定理2假设路网有NN个节点，NL条链接，每一个节点平均有NAC个链接，起点数量为NS，并且一个涟漪通过一个链接平均花费NATU个单位仿真时间。那么基于RSA的CEPO方法的计算复杂度为O(NS×NL×NATU)。

证明首先，路网的动态变化因具体问题的不同而相差甚远，因此本文不作考虑。其次，本文假设路网矩阵[M k|0,T k|0,Wk|0]能够得到立即更新，事实上可以通过其他相应的灾害动态环境模型来计算得到，因此对[M k|0,Tk|0,Wk|0]的计算更新不属于本文算法的计算任务。那么，RSA只需要完成链接扩散的计算过程。RSA的基本计算过程由一个根据涟漪扩散速度更新涟漪半径的加法运算和一个将涟漪半径与链接长度进行对比的比较运算组成。因为每个节点产生的涟漪不超过NS个，因此可以推断出，在找到最短路径之前的计算复杂度大约为NS×[NAC×NATU+(NN-2)×(NAC-1)×NATU]，所以其计算复杂度可以表示为O(NS×NN×NAC×NATU)。因为NL=NN×NAC，因此基于RSA的CEPO方法计算复杂度可以表示为O(NS×NL×NATU)。

与之相比，考虑到DPO方法的本质是一对一迭代计算，在求解多对多问题时采取遍历所有起点终点组合的计算方式，因此要计算NS×ND种组合方式(NS、ND表示路网中的起点、终点数）。类比于CEPO方法，DPO方法的计算复杂度为O(NS×ND×NL×NATU)。事实上，由于终点（即，受灾居民点）数量ND可能成百上千，因此CEPO方法和DPO方法在计算复杂度上的差异不可忽视。

4 海南岛台风情景案例分析

为了验证本文所提出的基于RSA的CEPO方法在解决动态灾害环境下多对多路径优化问题上的效果，本文基于海南岛的台风情景进行案例研究。

4.1 案例情景描述

中国拥有1.8万公里长的海岸线，是一个名副其实的海洋大国。在享受海洋带给人们益处的同时也遭受着诸如热带气旋等海洋灾害。有数据指出，建国初至2009年，登陆我国沿海的热带气旋平均达到9.2个/年，我国已经成为世界上热带气旋登陆最多、受海洋灾害最严重的国家之一[16]。每当热带气旋来临，海南因其特殊的地理位置首当其冲。为了保障台风来临时的物资供应，需要在台风将要登陆乃至已经登陆的情况下用最短的时间将物资安全运送到不同配送点，这就涉及到了动态灾害环境下的多对多路径优化问题。

目前，海南省已经完成了应急物资储备中心的建设，形成以三亚、海口、儋州、万宁和五指山为中心，覆盖全省的救灾物资储备网络[17]。为了模拟台风来临时的物资配送情况，在每个应急物资储备中心覆盖的区域内选取了有代表性的地市作为配送点，以此来做对比验证。应急物资储备中心的详细情况如表1所示，并在图5（a）中标明。

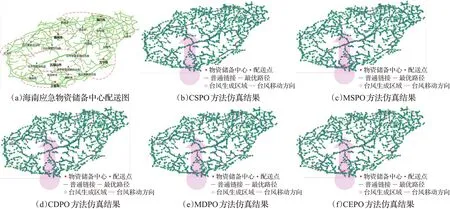
图5 物资储备中心配送图及不同方法仿真结果Fig.5 Distribution map of material reserve center and simulation results of different methods

表1 海南应急物资储备中心情况Table 1 Situation of Hainan emergency material reserve center

台风是一种复杂的极端天气现象，其形成及移动过程受到台风边界结构、下垫面及大气环境因子等诸多因素的影响，其基本参数的确定同样复杂。与此同时，不同台风的移动速度、影响范围及移动方向对最优路径的计算结果起着决定性的影响。本文综合了学者在相关领域的研究来确定台风的关键参数[18-20]。为了构建动态灾害环境，本文基于海南岛实际路网环境，构建了台风动态灾害模型。为了简化验证实验，本文设定台风从三亚市登陆，沿正北方向移动、移动速度为16 m/s、受影响区域为直径60 km的规则圆形。与此同时，本文约定台风所及之处路网不可通达，台风过境即恢复通达，因此路网通达性随台风的移动而时刻变化。

4.2 仿真实验及结果分析

为了更好地验证本文所提出的CEPO方法，本文与SPO方法和DPO方法做了对比。目前应用广泛的SPO方法无法直接应用于灾情的动态变化情景，并且人为划分配送范围（如表1所示），这极大降低了实用性。虽然可以通过引入等待行为对SPO方法进行改进，但物资配送范围的限制使其在动态灾害情景中一般会丧失全局最优性。为了使路径规划适应动态灾情的变化，大家通常利用DPO方法实现基于灾情变化的路径实时规划。但是，DPO方法的实质是一对一问题的迭代求解，为了求解多对多问题，需要通过采用遍历所有起点终点组合的计算方式对其进行改进，以打破SPO方法中物资配送范围的限制。但需要指出的是，由于DPO方法基于当前路网环境进行路径规划，因此其当前的计算结果通常并不适用于未来的路网环境，所以，其结果也没有理论最优性的保证。不同于SPO方法和DPO方法，CEPO方法在路网中所有物资储备点同时产生初始涟漪，所有涟漪在搜索过程中相互竞争，根据最先到达配送点的涟漪回溯得到最优路径，因此CEPO方法不考虑物资储备点服务范围的限制。而且，CEPO方法通过植入动态灾害模型进行协同路径规划，从而保证了结果的理论优越性。

为了更好地验证CEPO方法的可行性，本文基于Matlab利用考虑物资储备点服务范围限制的静态预案规划方法（CSPO）、改进后的静态预案方法（MSPO，即，加入等待行为）、考虑物资储备点服务范围限制的动态路径规划方法（CDPO）、改进后的DPO方法（MDPO，即，不再考虑物资储备点服务范围限制），以及CEPO方法针对台风案例进行对比实验，目的是比较上述方法所求解出的最短路径、最短运输时间，以及所需计算时间。最终结果如图5所示。除此之外，考虑到动态灾害对路网环境的影响，路径规划应用失败存在路径规划失败和路径规划成功但应用失败两种情况，因此本文定义路径规划应用成功率（即，路径规划成功并应用成功的数量占规划路径总量的比率）来衡量不同方法对动态路网的适应能力。在CSPO方法中考虑了配送范围的限制并且物资储备点与配送点一一对应，这极大降低了路径规划应用成功率，因此本文引入物资储备点到配送点的对应率（即，规划路径的物资储备点到配送点的对应关系与CSPO方法相一致的比率）来衡量不同方法的灵活性。表2列出了五种方法的详细数据，其中包括路径规划应用成功率、物资储备点到配送点的对应率、最优路径总长度（PL）、运输耗时（TT）和计算耗时（CT），表3、4、5分别列出了利用不同方法求解得到的到所有物资配送点的规划路径长度（PL）、运输耗时（TT）和计算耗时（TT）。

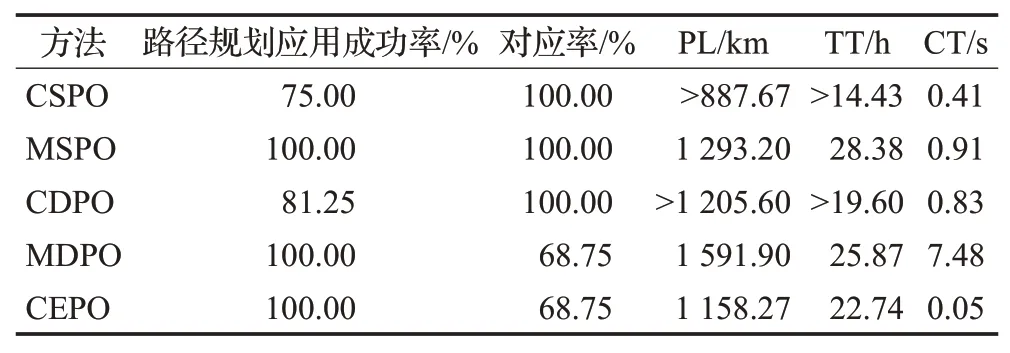
表2 不同方法仿真实验平均结果数据对比Table 2 Comparison of average results of different simulation experiments

根据上述仿真实验可以得到如下结论：

（1）动态灾害环境下的路径规划应用成功率是路径优化问题首先要考虑的问题。CSPO方法的应急救援物资配送都有着固定的运输路线。显然，这样事先规划好的路径没有考虑也就无法适应灾情的动态变化，从而可能无法成功应用，如表2所示CSPO方法路径规划应用成功率只有75%。表2中关于CSPO方法的数据只是基于规划应用成功的静态预案路径计算得出的，考虑到规划应用失败的静态预案路径的数据可以视为无穷大，因此相关数据前面有一个“＞”符号。MSPO在静态预案方法中加入等待行为可以保证100%的规划应用成功率。CDPO方法的规划应用成功率为81.25%。MDPO会遍历所有起点终点组合，因此不再受配送点服务范围限制，所以其规划应用成功率为100%。CEPO完全不考虑静态预案方法中配送点服务范围的限制，所以路径规划应用成功率也为100%。

图5直观展示了不同方法所得到的规划应用成功率问题。由图5可知，由于台风登陆与路径优化同时进行，因此三亚市首当其冲。结合图5（a）、（d），虽然抱龙林场、保港镇和藤桥镇三个物资配送点在三亚市的物资配送范围内，但是在CDPO方法下，上述三地受动态灾害的影响无法得到物资配送，而且三亚也失去其物资储备中心的能力。与此同时，如图5（c）、（e）、（f）所示，MSPO保证了配送范围内的应急物资的供应，MDPO和CEPO则从其他物资储备中心保证应急物资的供应。如表3所示，CEPO方法能够主动打破物资配送点服务范围的限制。这是因为RSA算法的本质是涟漪扩散接力赛，在物资配送点产生初始涟漪同时向四周扩散，并且扩散过程只与路网情况有关而不会考虑服务范围的限制。需要指出的是，一味的强调物资储备中心的服务范围是没有意义的，尽快将应急救援物资安全送到配送点才是需要重点考虑的问题。

（2）关于所规划路径的长度，如表2所示，MSPO、CDPO和MDPO分别比CEPO方法多11.65%、4.09%和37.44%，CSPO比CEPO少23.36%。但需要注意的是，CSPO和CDPO方法分别存在25%和18.75%的配送点路径规划应用失败的情况。这是因为CSPO、MSPO和CDPO方法考虑了配送范围的限制，因为路网分布的不均匀性，物资储备点和配送点之间直线距离最短不等同于规划路径长度最短，因此其结果为局部最优而非全局最优。MDPO方法虽然可以在没有配送范围限制的情况下进行路径规划，但它实时在线优化的特点也没有最优性保证，例如，表3中到乐东黎族自治县的MDPO的规划路径长度为CEPO方法的141.77%。然而CEPO方法能够保证结果的全局最优性，因此如表3所示，CEPO方法到所有物资配送点的最优路径长度为所有方法中最短的。

（3）运输耗时的长短是路径优化要重点考虑的问题。虽然运输速度恒定，但是考虑到MSPO和CEPO方法在路径搜索中引入了等待行为，所以其规划路径长度与运输耗时的比值并不完全恒定。如表2所示，MSPO和MDPO方法运输耗时比CEPO方法多24.80%和13.76%。MSPO方法虽然规划路径长度比MDPO方法短18.76%，但运输耗时却多9.70%。这表明，MSPO方法虽然在规划路径长度上占有优势，因为在路径搜索过程中加入了等待行为，在运输耗时上反而有很大不足。与此同时，CEPO方法却能兼顾较短的规划路径长度和较少的运输耗时，这表明了CEPO的路径规划效果最佳。事实上，CEPO方法引入的等待行为可以有效避免不必要的绕路行为，再加上CEPO方法能够打破配送范围的限制保证全局最优性，因此其规划的规划路径长度更短、运输耗时更少。

（4）关于计算耗时，CEPO分别为MSPO、CDPO和MDPO的5.49%、6.02%和0.67%。这是因为CEPO基于RSA算法，其原理更为简单且计算量更小，因此CEPO方法在计算时间上有着明显优势。MDPO方法的实质是一对一问题的迭代求解，其计算复杂度比CEPO方法更高。如表5所示，除保港镇和乐东黎族自治县配送点外，MSPO、CDPO和MDPO针对每一个配送点的计算耗时基本相同，总耗时主要取决于迭代次数。

4.3 随机路网实验

为了使本文提出的基于RSA的CEPO方法在求解动态环境下多对多路径优化问题上的优越性更具有说服力，本文使用随机路网进行实验验证。

本文在[－1 000 1 000－1 000 1 000]范围内生成4 900个节点的随机路网，并且每个节点有6条链接相连。考虑到路网的动态变化，分别在[－300 1 500]、[－1 500－300]和[1 500－700]生成直径为200的障碍区域，并在图6所示的方向以20的速度匀速运动。在多对多问题中，往往存在多个起点和多个终点，因此，如图6所示，本文设置了不同的起点、终点对（需要指出的是，起点、终点对没有固定的对应关系，仅仅实际距离较近）。

图6 4 900个节点的随机路网环境Fig.6 Random network environment with 4 900 nodes

如表6为基于随机路网环境下利用不同方法得到的SRPPA、CR、PL、TT和CT。可以得到，只有MSPO和CEPO方法得到的SRPPA始终保持100%。这是因为二者都加入了等待行为，即，当路网不可通达时节点呈等待状态，直到路网恢复通达时继续完成路径搜索过程。结合PL和TT可知，CEPO方法在保证100%的路径规划成功率的前提下实现了更短的运输时间，这具有更强的实际应用价值。最后，本文注意到CEPO方法因其计算方式更为简单，在CT上与其他方法相比具有数量级上的差别，这使得计算结果具有更好的时效性。

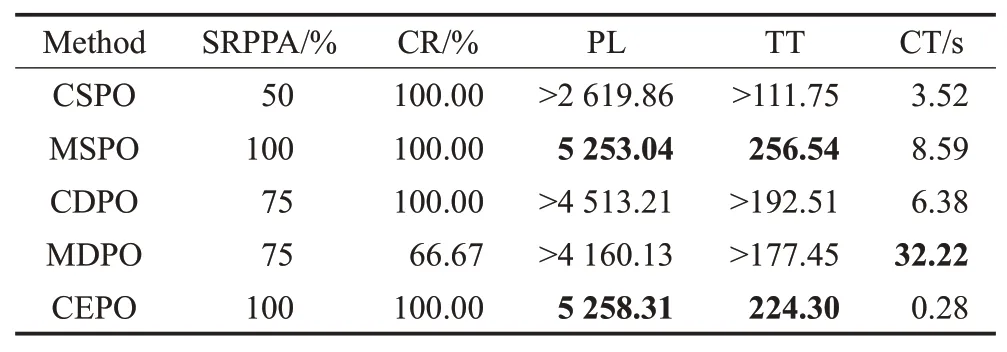
表6 随机路网环境下不同方法实验结果对比Fig.6 Comparison of experimental results of different methods under random routing environment

4.4 实验结论

通过对海南岛台风情景案例和随机路网案例应用不同方法进行对比仿真实验对比，可知：CEPO方法打破了物资配送范围的限制，可以得到动态灾害环境下多起点多终点的最佳对应关系，兼顾了较短的规划路径长度和较低的运输耗时，并且达到了100%的规划应用成功率。CSPO方法因为受到物资储备点服务范围的限制，所以规划应用成功率较低。MSPO方法虽然通过引入等待行为可以获得100%的规划应用成功率和较短的规划路径长度，但是盲目的等待增加了运输耗时，即在灾害环境中的暴露时间增长，从而增大了运输过程中的风险。CDPO方法受到物资储备点服务范围的限制，无法保证100%的规划应用成功率。MDPO方法通过采取遍历的计算方式保证了100%的规划应用成功率，但无法保证结果最优性，其规划路径长度和运输耗时较长。

综上所述，CEPO在动态灾害环境下求解多对多问题时由于RSA算法特点，相比于CSPO、MSPO、CDPO以及MDPO在规划应用成功率、求解时间和求解结果的最优性、时效性、灵活性上都有优势。

5 结论及后期工作

面对动态灾害环境下多对多物资配送路径规划问题，现有的CSPO方法、MSPO方法、CDPO方法和MDPO方法都存在一定局限性，无法兼顾求解时效性、最优性以及应用成功率。本文提出利用采取基于RSA的CEPO方法来解决该问题。RSA算法采取涟漪接力赛的形式形成涟漪之间的相互竞争，所以该算法面向仿真时间分析的特性可以将路径搜索过程与路网动态变化过程相结合。因此，CEPO方法可以通过一次计算得到动态环境的理论最优路径，打破配送范围的限制并通过引入等待行为有效避免绕路的风险，保证结果的理论优越性和时效性。在后续研究中，通过完善路网模型进一步验证CEPO方法的有效性，通过完善动态灾害模型进一步扩展CEPO方法的应用范围并做进一步推广。