特征点提取下的AGV栅格法建模与分析
赵 江,孟晨阳,王晓博,郝崇清,李 冉,刘慧贤,王昭雷
1.河北科技大学 电气工程学院,石家庄 050018
2.国网河北省电力有限公司,石家庄 050051
自动引导车(AGV)是一种具有安全防护和多种装载功能的运输小车。它有多个自动引导装置,可以按规定的路径行驶[1]。由于AGV既可以应用于码头的自动装卸,又可以提供家庭服务[2],近年来受到越来越多的关注。由于路径规划是AGV实现功能的基础,所以该问题也成为机器人领域研究的热点。路径规划是指在具有障碍物的环境约束下,根据给定的起点和终点,应用算法准则,为AGV找到一条最优或接近最优的、安全、无障碍路径[3-4]。AGV路径规划可分为静态规划和动态规划两种。其中静态路径规划也称为全局或离线路径规划,所有的环境信息均为已知;动态路径规划问题则是基于传感器对周围环境的感知,由于其环境信息为全部未知或部分未知,也被称为局部或在线路径规划问题。本文研究的是已知环境下的全局静态路径规划问题,通过选择栅格法来解决这类问题。
解决静态路径规划的主要方法有粒子群优化算法[5]、蚁群算法[6]、A*算法[7]、人工势场法[8]等,这些算法通常在栅格图环境模型中对路径进行搜索。其中蚁群算法是一种概率仿生算法,随着种群的迭代得到最优路径[9];A*算法是一种启发式路径规划算法,它通过判断从起点到当前点的距离和从当前点到终点的距离的启发式信息之和来寻找最优路径[10];人工势场法是一种虚拟力法[11],它通过引力和斥力的相互作用将AGV引向终点。研究人员对上述算法进行了大量的研究,并提出了许多优化方案。
传统的蚁群算法存在迭代次数多、搜索效率低等缺点。为了解决这些问题,Lee[12]提出了一种基于异构蚁群的路径规划方法,该方法改进了蚁群的转移概率函数和信息素更新规则,在不需要后续平滑处理的情况下可以直接找到节点数较少的最优路径;Zhang等[13]提出了一种智能蚁群路径规划算法,该方法通过消除蚁群算法中禁忌表的约束,引入临时权值矩阵,避免了小权值路径的重复选择,提高了算法的效率;Lee等[14]改变了蚁群算法生成初始种群的方式,缩短了寻找最优解的时间,加快了算法的收敛速度;Saidi-Mehrabad[15]将蚁群算法分为两个阶段进行路径搜索,有效地缩短了路径规划的完成时间。
传统的A*算法搜索过程盲目,规划出的路径转弯次数过多,导致AGV的运行损耗过大。为了解决这些问题,Yu等[16]提出了一种蚁群优化算法和A*算法相结合的双层算法,其中蚁群算法负责确定目标的移动顺序,A*算法负责快速建立目标之间的移动成本图,以便于蚁群算法的计算;Song等[17]发现A*算法规划的路径包含大量的拐点,在实践中会影响AGV的运行,因此提出了一种改进的A*算法,并在规划后对路径进行了平滑处理。
为解决传统人工势场法局部最优问题,Sudhakara等[18]在人工势场法的基础上,提出了一种不考虑排斥力和吸引力影响的优化算法,通过构建一种排斥函数产生排斥势场,并将其应用于任意形状的障碍物上,通过该方法可以为移动机器人提供更为准确的路径;Orozco-Rosas等[19]提出将遗传算法与人工势场方法相结合,找到一条可行的安全路径;Zhou等[20]提出用粒子群算法改进人工势场法,引入切向量对规划出的路径进行优化,并在人工势场模型中加入基于障碍物信息的矢量来辅助完成避障过程,大大改进了人工势场法的局部最优问题。
利用上述改进算法在栅格图中进行路径规划的本质仍是比较所有相邻无障碍栅格的估计函数,即计算栅格图中每个相邻可行栅格的估计函数,然后通过比较估计值得到下一个路径点。这种逐点规划的方法存在着大量的无效计算,导致算法的效率大幅降低。为了解决这一问题,卜新苹等[21]采用四叉树方法对传统栅格图进行分割,减少栅格的数量,并对分割后栅格的连接关系进行定义,结果表明,减少栅格数可以在不影响路径质量的情况下缩小搜索范围,提高算法的计算效率,并减少路径中的节点数。Han[22]提出了一种关键障碍物及其周围点的提取方法,该方法根据障碍物的不同重要性,在环境中找到相对重要的障碍物,并找到与这些障碍物相关的栅格点,从而降低了三维路径规划的复杂度,大量仿真实验表明,该方法可以提高三维路径规划的效率,并减少路径中拐点的数量,从而提高移动机器人的运行效率。
在使用四叉树方法对栅格图进行分割时,对于不同的环境和不同的路径规划要求会有不同的分割原则,并且在重新建立栅格间的连接关系时,频繁的入栈和出栈操作可能会导致计算量过大。而提取关键障碍物及其周围栅格点的方法仅适用于对一条路径进行微调,在寻找不同的路径时,栅格间的重要性关系会发生改变,从而影响路径规划的过程。为了解决上述问题,本文提出了一种基于特征点提取的环境建模方法,该方法通过提取每个障碍物的顶点栅格作为特征点对环境进行建模,以期得到一个更为简化且适用面更广的环境模型,从而有效地缩小路径规划算法的搜索范围,提高算法的搜索效率,得到一条更为优化的路径。
1 传统栅格法建模及其改进
1.1 传统栅格模型的建立
在进行路径规划前,需要对AGV的运行环境进行建模。选择的建模方法通常为栅格法,栅格法建模的方法如下。
对机器人运行环境进行量化处理,形成一些以AGV投影尺寸为单位的小单元,作为一个环境的网格映射。根据环境的大小设置相应的网格映射为m×m。网格映射模型如图1所示。图中红色为起点,绿色为终点,黑色网格表示量化后的障碍物。该图所示起点坐标表示为S=( 4 .5,4.5),终点坐标表示为E=(1 5.5,15.5)。

图1 栅格法建模图示Fig.1 Grid model diagram
栅格图内的每个格都可以设定为一个小的单元,数学表达为cell(x,y),其中x、y表示每个小单元的位置。根据每个网格是否为障碍物,给每个单元设置为:
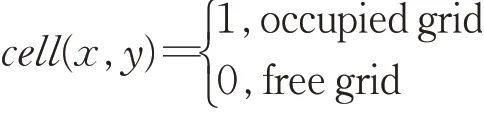
当机器人遇到障碍物的时候将当前单元格记录为1,表示障碍物栅格。相对于障碍物栅格其他的栅格为0,表示可行栅格。栅格还可以储存机器人路径信息,表示为相关属性和访问属性,同样栅格也可以记录自身特殊信息。
1.2 传统栅格模型的路径规划
建立环境模型后,需要确定AGV的起点和终点。如图2所示,S为起点,E为终点,找到一条从S到E的有效路径,这个过程称为路径规划。

图2 传统栅格图中的路径规划Fig.2 Path planning in traditional grid graph
传统的AGV路径通常根据特定的性能指标(最短路径、最短时间、最小损耗等)进行规划。但在实际应用中,不仅要考虑路径长度和运行时间,还要考虑AGV运行时的磨损、与障碍物之间的安全距离和算法的计算效率等。而在AGV的实际运行中,由于规划的路径通常是分段线性路径,AGV必须在每个换向节点处停止,根据下一个路径改变其方向,然后重新启动。基于传统栅格图的路径规划方法在寻找最短路径时往往忽略了节点过多而造成的影响。因此,减少换向节点对提高AGV的运行效率和减少AGV的磨损具有重要的作用。
另外,基于传统栅格法建模的路径规划算法在搜索路径时,往往通过判断当前节点周围的节点信息来选择下一个节点。要计算的栅格数随着栅格图分辨率的增加而增加,从而降低了搜索速度。
为了使算法在不影响解的质量的情况下提高对路径搜索的目的性,本文提出了一种基于特征点提取的栅格图模型,以减少算法的计算量,使AGV的路径更加平滑。
1.3 基于特征栅格提取的栅格模型
(1)特征提取规则
在路径规划问题中,只要起点和终点互不可见,基于栅格法规划出的最短路径的有效拐点往往是障碍物栅格的顶点。然而,由于逐层规划的弊端,有效拐点之间往往存在大量无效拐点。当两个可相互到达的有效拐点之间的路径是一条线段时,该路径为两个有效拐点之间的最佳路径,因此将特征栅格提取规则定义如下:
规则1特征栅格可以是与单个黑色栅格的四个顶点处相对应的可行栅格。
规则2特征栅格也可以是与组合黑色栅格的所有凹角处相对应的可行栅格。
规则3特征栅格数量应与障碍物栅格数量相关,障碍物数量越多特征栅格数量越多。
(2)障碍物网络模块化处理
结合特征栅格提取规则,本文利用蒙特卡罗搜索的方法来分析处理环境栅格模型,利用各种网络模型来合理区分各种类型的障碍物栅格,由蒙特卡洛搜索分解出的基本障碍物栅格如图3所示。
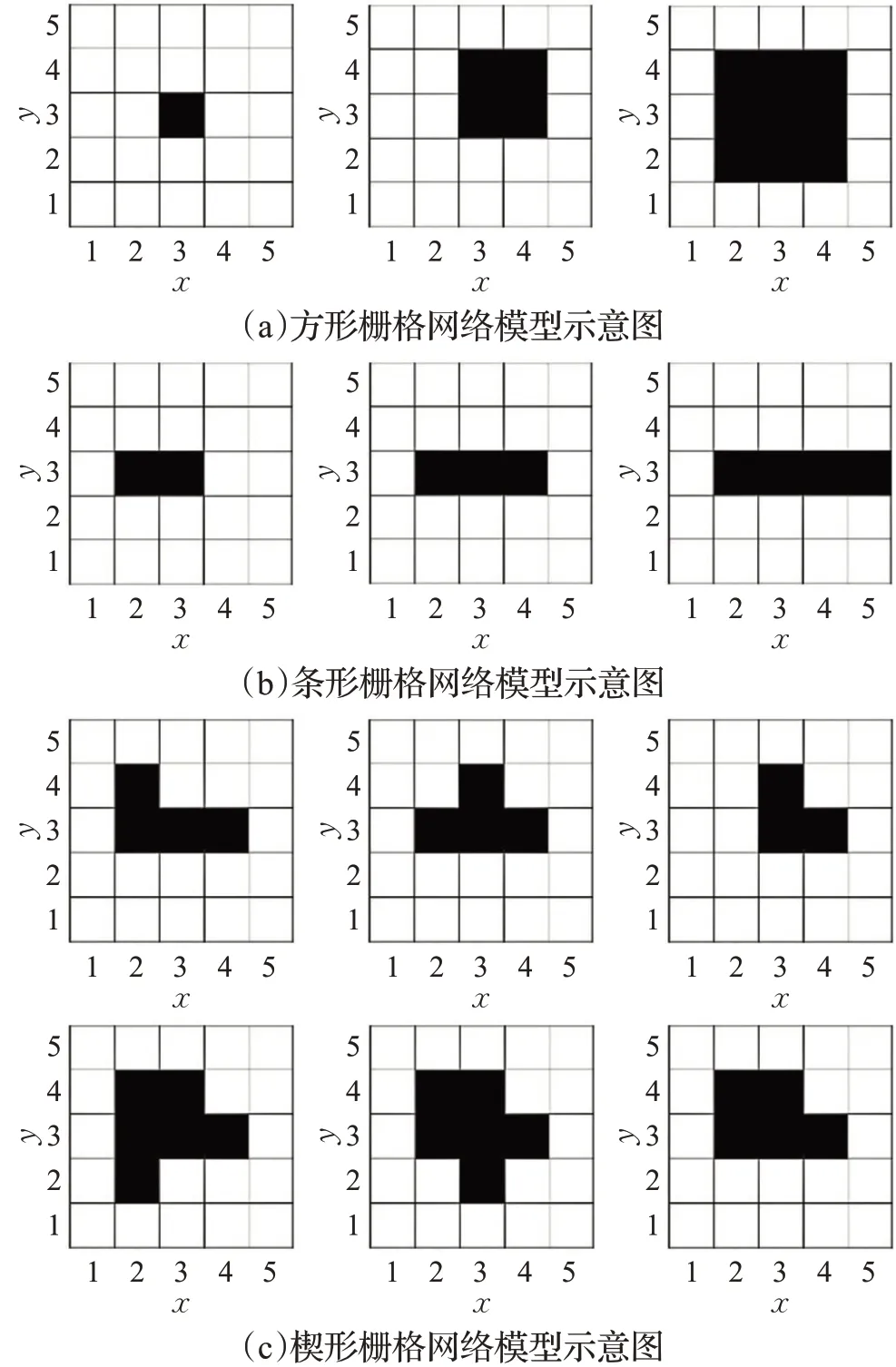
图3 网络模型化处理下的障碍物示意图Fig.3 Obstacle diagram based on network modeling
通过蒙特卡洛模拟可以得出上述十二种基本障碍物形状,其可以组合出栅格法建模中任意障碍物形状。通过特征栅格的提取规则可以得出各种障碍物形状对应的特征栅格。结合特征提取规则,任意环境中都可以提取出相应的特征栅格,特征栅格可以代表栅格法路径规划的全部环境信息。
栅格法建模是将AGV运行的工作环境单元分割为大小相等的方块,形成一组网格,网格图中每一个栅格都可以作为一个二值信息网格单元来存储环境信息,这些信息可以包含人为指定信息,也可包含算法规划信息,每个网格被称为环境单元。栅格法建模将整个环境进行抽象建模,路径规划时采用相应的路径规划搜索算法在该空间内进行搜索。通过特征提取规则选择特征栅格,其周围都会有白色可行栅格,特征栅格可以表示周围白色可行栅格的环境信息。基于栅格法规划出的最短路径中的有效拐点往往是黑色栅格对应的可行顶点栅格,而其他栅格只是作为可行栅格进行规划,特征栅格可以很好地表达周围白色可行栅格的环境信息,在简化环境模型的同时,保证了环境信息的完整性。
(3)新型栅格法建模结果
基于上述规则和栅格建模方法,可以得出在栅格建模环境下,膨胀化的障碍物是由多个正方形组成的不规则图形,由提取规则1、2,特征栅格的数量应与障碍物栅格数量相关,即障碍物栅格数量越多特征栅格数量越多。根据规则1、规则2和规则3提取特征网格,提取结果如图3所示。
由图4可知,从6×6网格模型中提取了10个顶点,搜索范围从25个栅格缩小为10个栅格,减少了栅格法建模产生的60%无效栅格,新型栅格法建模减少了算法的搜索范围,局部路径规划算法只需要对特征栅格进行路径规划,大大提高了算法的搜索效率。

图4 特征栅格提取Fig.4 Feature grid extraction
在提取顶点后,大部分提取的栅格不再是连续栅格,因此需要通过栅格可见性判断的方法重建每个栅格的邻接矩阵。栅格之间的连接可以分为三种类型,如图5所示。

图5 栅格可见性判断Fig.5 Grid visibility judgment
类型一:图中的栅格a和b之间没有障碍物,皆为白色栅格,因此,定义栅格a和b是可见的,线段l1为可行路径。
类型二:图中的栅格a和c之间有障碍物,存在黑色栅格,因此,定义栅格a和c是不可见的,线段l2为不可行路径。
类型三:图中的栅格a和d之间虽未直接经过障碍物栅格,但线段l3却与黑色障碍物栅格交于点(1,2),由于AGV自身存在体积,为了AGV运行时的安全性,该类路径应被定义为不可行路径,然而,在传统的基于栅格法的路径规划算法中,并没有将该类不可行路径排除,使AGV的运行路径存在隐患,所以本文提出的将该类路径定义为不可行路径的方法,一定程度上提升了AGV运行时的安全性。
1.4 新型栅格法建模性能分析
栅格环境建模方法是将机器人周围空间分解为互相连接且不重叠的空间单元,空间单位可以表示为栅格,栅格法建模分为精细化栅格法和近似化栅格法两种方式。新型栅格法建模属于近似栅格法建模,将障碍物做膨胀化处理,栅格不仅可以完整地保存环境信息还可以保证AGV在环境中的运行安全。新型栅格法建模提取的是黑色栅格顶角位置的白色栅格,由于栅格法对障碍物膨胀化处理,通过特征提取到的白色栅格保证了原有栅格法建模对环境信息的完整性,并且保证了AGV在环境中的运行安全。
相对于传统栅格法建模中将全局环境作为有效信息输入到AGV的路径规划中,新型栅格法建模大量减少了传统栅格法中需要运算搜索的栅格数量,使用30%~40%的特征栅格就可以表示全局环境信息。图6中,数字标出的是特征点提取下的有效栅格,障碍物边缘是路径规划算法运算的重要位置,将重要位置提取出来,不仅可以保证环境信息的完整性还可以保证AGV路径规划的搜索速度。同时使得AGV的搜索更加具有目的性,并结合传统栅格法建模的优点,保证了AGV运行的安全。

图6 新旧栅格法对比分析Fig.6 Comparative analysis of new and old grid method
针对局部路径规划算法,如蚁群算法、A*算法和人工势场法等需要对每个白色栅格进行算法估计,而黑色栅格顶点处白色栅格上的局部路径规划算法估计值变化巨大,新型栅格法建模选择提取单个黑色栅格的四个顶点处相对应的可行栅格和组合黑色栅格的所有凹角处相对应的可行栅格作为特征栅格,可以保证特征点具有代表性。
1.5 新旧路径对比分析
基于特征点提取的思想,将传统栅格图中的障碍物顶点选为特征点提取出来,在进行了顶点可视性判断、确定顶点间的连接关系之后,重新在该环境下进行路径规划,得到的结果如图7所示。
在图7中,黑色路径是传统栅格模型中规划的路径,红色路径是特征栅格提取的环境模型中规划的路径。

图7 新旧路径对比分析Fig.7 Comparative analysis of old and new paths
两条路径之间的主要数据比较如表1所示。从路径长度上看,相比于传统栅格图下的路径规划算法,基于特征栅格提取的栅格法规划出的路径由于搜索范围被严格约束在了障碍物的顶点上,在进行路径规划时会大概率选择路径ab,而不选择路径acb。由三角形法则可得,在三角形abc中,ac+cb>ab,最终使得路径长度变短;从换向节点数和路径总转角上看,由于特征栅格提取的栅格图中,路径从栅格a到b没有经过c,减少了拐点c之后,由d到g减少了三个90°的拐角,转化成了两个45°的角,使得路径总转角大幅减少,从而减少了AGV运行时的损耗;从平均安全距离上看,基于特征点提取的栅格图中加大了路径的平均安全距离,有利于AGV的安全运行。

表1 新旧路径的主要数据对比Table 1 Comparison of main data between old and new paths
2 新环境模型在典型路径规划算法中的应用
为了验证所提出的环境建模方法的有效性,将其应用于多种不同类型的路径规划算法中,包括虚拟力法、直接搜索法和进化算法,并解决算法中存在的运行时间长、局部最优等问题。栅格法为全局搜索算法,新型栅格法适用于基于先验完全信息的局部路径规划方法,例如A*算法(直接搜索法)、人工势场算法(虚拟力法)和蚁群算法(进化算法)等。
2.1 新栅格模型在人工势场法中的应用
人工势场法是Khatib提出的一种虚拟力法,其思想是将AGV、目标点和障碍物视为质点,将AGV运动环境抽象为一个具有吸引力和排斥力的力场。在这个力场中,障碍物提供排斥力,目标点提供吸引力,根据AGV的位置产生合力决定AGV的运动方向,其实质是根据环境建立一个模拟力场。
人工势场法的数学模型如式(1)所示:

式(1)中,U为小车的势能之和,Uatt为目标点对AGV的吸引力,Urep为障碍物对AGV的排斥力,再将引力场对AGV的引力梯度和斥力场对AGV的斥力梯度通过拉格朗日变换得出力的关系为:

式(2)中,Fatt为目标点对AGV的吸引力,Frep为障碍物对AGV的排斥力,AGV所受的合力如图8所示。
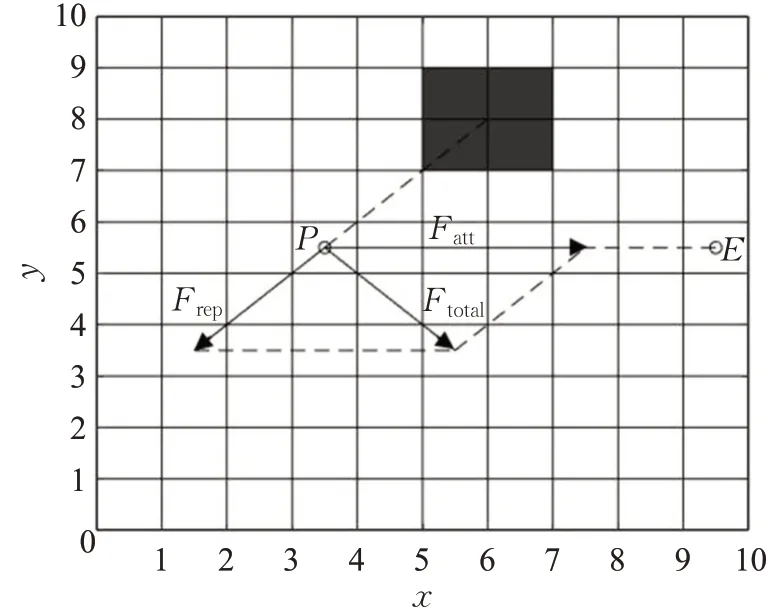
图8 栅格图中AGV所受合力Fig.8 Resultant force of AGV in grid graph
设AGV在工作空间中的位置为p=(x,y)T,则其引力势函数为:

k为大于零的引力势场常量,p为AGV位置向量,pe为AGV在势场中的目标位置,则引力势函数的负梯度为:

该引力随着AGV趋近于目标点而趋近于零。根据Khatib提出的一种FIARS函数得出斥力势场公式如下:

式(5)中,η为当前障碍物对AGV有影响时的斥力势场常量,ρ为AGV所在位置与障碍物的最短距离,ρ0为单个障碍物所能影响的最大距离范围,当AGV与障碍物的距离大于ρ0时斥力场对AGV的影响为零。斥力场产生的斥力为:

根据上述理论依据可得人工势场法的基本流程如下:
步骤1参数初始化:设置引力常量、斥力常量、起点以及目标点。
步骤2获取当前AGV状态,根据公式(2)判断此时机器人的受力情况,确定接下来AGV的移动方向。
步骤3判断AGV是否到达目标点,如果到达,则结束程序,否则返回步骤2。
虽然人工势场法能有效地解决AGV与障碍物的碰撞问题,但传统的人工势场法路径规划方法仍存在以下问题:(1)当AGV移动到某一位置时,吸引力和排斥力之和为零,AGV会错误地认为已经到达了目标位置并停止,这是一个典型的局部最优问题;(2)传统人工势场法产生的路径会频繁经过障碍物的边缘,无法保持有效的安全距离,从而影响AGV的安全运行。
为了解决上述问题,将基于特征点提取的栅格模型应用到人工势场法中。由于该栅格模型的引入,由AGV所受到的合力确定AGV运动方向的方法不再适用,所以不再计算每个栅格的各个方向的合力,而是计算其势能,然后通过势能下降的原理确定AGV的运行方向。
在栅格模型中利用人工势场法规划路径时,通常对每个栅格赋值,将导致AGV的运行在环境中缺乏有效的信息导向。因此,根据本文提出的特征点提取的栅格模型,在计算势能时,只需计算提取的特征栅格的势能,这样可以为AGV的运行提供更有效的信息指导,从而解决人工势场法路径规划中的局部最优问题,提高AGV与障碍物之间的安全距离,保障AGV运行时的安全。
通过对人工势场法在新型栅格图中的应用,可以看出新型栅格图可以很好地解决应用虚拟力法时移动机器人的路径规划问题,对于以模拟退火算法和人工势场法为代表的虚拟力法具有很好的适用性。
2.2 新栅格模型在A*算法中的应用
A*算法是一种根据给定的代价函数,在静态环境中寻找从起点到目标点最优路径的一种直接搜索方法。并通过在Dijkstra算法中加入启发式函数,提高算法的计算效率,其数学模型为:

式(6)中,f(x)是从起点S通过x位置到达终点E的最优成本,g(x)表示从位置S到目标点x的实际成本,h(x)表示从目标点x到终点E的估计成本。如图9所示,所以估计成本中min(f(x))被选择的概率较高。因此,A*算法在规划路径时总是选择min(f(x))的节点。

图9 利用A*算法进行路径规划Fig.9 Path planning using A*algorithm
每个栅格左上角的数字表示最优成本f(x),左下角的数字表示从起点S到位置x的实际成本g(x),右下角的数字表示从位置x到目标点E的估计成本h(x)。
根据上述理论依据可得A*算法的基本流程如下:
步骤1初始化参数,设置开发列表Q,设置起点和终点。
步骤2根据公式(6),选择Q中的最小f(x)的节点x作为下一个路径点。
步骤3确定搜索是否已到达终点,如果是则停止算法,如果不是则转到步骤4。
步骤4搜索扩展,对图中每两个节点m、n进行比较。如果g(m)>g(n)+cost(n,m)则g(m)=g(n)+cost(n,m),f(m)=g(m)+h(m),并将m点加入到开放列表Q中,否则,m点不加入到Q中,返回步骤2。
A*算法在Dijkstra算法中增加了一个启发式函数。尽管A*算法有效地减少了搜索范围和计算复杂度,但它仍然需要估计栅格图中每个节点的距离,用h(x)表示当前节点和目标节点之间的成本,并通过选择最小的f(x)来选择最优路径。当环境较大时,栅格图中大量的栅格将延长A*算法的搜索时间。因此,采用新栅格法来解决这个问题。
首先提取障碍物的每个顶点栅格作为特征栅格,只计算特征栅格的估计值。A*算法在搜索栅格时,只搜索这些特征栅格,从而减少A*算法在栅格模型中搜索的栅格数,避免A*算法搜索时间过长和范围过大。另外,由于新的栅格建模方法提取的特征栅格不再是简单的水平或垂直关系,因此使用欧几里德距离代替曼哈顿距离来计算估计值,该方法还可以有效地减少规划出的路径的转弯次数和角度。
将新型栅格法应用于A*算法中可以有效减少A*算法的搜索面积,提高搜索速度,对于以A*算法和Dijkstra算法为代表的搜索算法有很好的适用性。新型栅格法建模有效提高了算法的性能。
2.3 新栅格模型在蚁群算法中的应用
蚁群算法是一种通过模拟自然界蚂蚁寻找最短觅食路径的仿生算法。每只蚂蚁在觅食时都会在路径上留下一定浓度的信息素,并且由于信息素会挥发,所以路径越长,信息素浓度越低。随后的蚂蚁更倾向于沿着信息素浓度较高的路径行走,并继续在路径上留下新的信息素。通过上述正反馈效应,最终蚂蚁们行走的路线将收敛到信息素浓度最高的最短路径上。蚁群算法的数学模型包括节点选择策略、信息素更新和邻接矩阵三个部分。
节点选择策略是指当蚂蚁位于栅格中时,为了从备选栅格中选择一个栅格进行转移,需要使用状态转移概率公式来选择下一个栅格,蚂蚁k从栅格i到栅格j的转移概率为:

其中,allowed k={c~-tabuk}代表每只蚂蚁下一步中的所有可选栅格,c~为所有栅格的集合,tabuk为第k只蚂蚁已经走过的所有栅格的集合,τij(t)为当前时刻i,j两个栅格之间在t时刻的信息素浓度,ηij(t)为启发函数,通常取ηij(t)=1/d ij,α为信息启发因子,表示信息素的重要程度,α越大蚂蚁之间的协作也就越强,β为启发式因子,表示启发函数的重要程度。
在路径搜索过程中,为了避免信息素浓度过高导致启发式信息失效,通常在搜索路径后需要对信息素进行更新。更新规则如式(8)和(9)所示:

其中,ρ∈(0,1)为信息素挥发因子,其大小关系到算法的全局收敛能力和收敛速度表示第k只蚂蚁在栅格i和j之间留下的信息素,有三种不同的蚁群算法模型,“蚁周系统”(Ant-Cycle)模型,“蚁量系统”(Ant-Quantity)模型和“蚁密系统”(Ant-Density)模型,其中蚁周系统算法性能优于其余两种算法,其公式如下:

蚁群算法通过邻接矩阵进行判断两点之间是否可达,在n×n的栅格图中,邻接矩阵D是一个大小为n2×n2矩阵,当i,j两个栅格之间不可形成路径时,D(i,j)=0,当i,j两个栅格之间可以形成路径时,D(i,j)=d ij。
根据上述理论依据可得蚁群算法的基本流程如下:
步骤1初始化α,β,ρ,M,N等参数。
步骤2将蚂蚁置于起点,并准备开始搜索路径。
步骤3通过式(7),在邻接矩阵D(i,j)≠0的栅格中选择下一个节点。
步骤4更新禁忌表tabuk。
步骤5判断所有蚂蚁是否都完成了搜索,如果完成搜索进入下一步,否则返回步骤3。
步骤6根据式(8)~(10)更新信息素。
步骤7判断是否达到最大迭代次数,如果是则输出最优路径,否则返回步骤2,开始新一轮的搜索。
蚁群算法作为一种生物进化算法,其收敛速度是评价算法性能的重要指标。然而,传统的蚁群算法存在收敛速度慢的问题。这是由于蚂蚁在搜索路径时需要考虑的路径数量庞大,大大影响了算法的计算效率。应用本文提出的基于特征点提取的栅格模型,可以在不影响求解质量的前提下,减少对差解的搜索次数,从而提高蚁群算法的收敛速度。
在蚁群算法中,栅格间的连接关系是由邻接矩阵D确定的。传统蚁群算法的邻接矩阵是通过判断该栅格周围的8个栅格是否为障碍物栅格求得的,设起点栅格为i,判断栅格i+1与其的连接关系时,只需判断栅格i+1是否为障碍物栅格或非相邻栅格,若是则邻接矩阵D(i,i+1)=0,若不是,则邻接矩阵D(i,i+1)=d i+1。而当将障碍物顶点作为特征点提取出来后,判断的不再是i与其相邻栅格的连接关系,而是所有的障碍物顶点栅格与栅格i的连接关系。通过第1章中提到的可视性判断,当栅格i与顶点栅格j可见时,邻接矩阵D(i,j)=d ij,否则D(i,j)=0。
将新型栅格法建模应用于蚁群算法时有效减少了算法的搜索次数,大大提高了算法的收敛速度,说明新型栅格法建模适用于以蚁群算法、粒子群算法为代表的概率型算法。
通过以上的理论分析,可以得出局部路径规划算法使用二值信息的网格单元来储存信息,都可以选择用栅格法为工作环境进行建模。例如栅格可以存储A*算法中每一个位置的估计值,也可以存储蚁群算法每一个位置的信息素浓度。当移动机器人选择可以使用栅格来存储算法信息的路径规划算法时,可以选择新型栅格法建模来完成环境建模。
3 仿真结果
为了验证新的栅格建模方法的适用性,将其应用于三种不同的路径规划算法:人工势场法、A*算法和蚁群算法中,并与传统栅格法的路径规划进行比较。
为了保证实验的客观性,仿真中只改变路径规划中各算法的环境模型,而不改变其具体的算法参数。栅格的边长设置为1,障碍物的密度和分布是随机产生的,在10×10、20×20和30×30的栅格地图上仿真并显示三组不同算法的结果。
3.1 新栅格法模型应用于人工势场法的结果
在三个栅格地图中,起点S的坐标分别为(0.5,0.5),(1.5,18.5)和(2.5,27.5),终点E的坐标分别为(9.5,9.5),(19.5,3.5)和(24.5,1.5)。设k为1.72,图10(a)、(b)和(c)上图显示了人工势场法在传统栅格法规划出的路径,下图显示了人工势场法在新型栅格法规划出的路径,其中黑色实线为规划路径。
从图10可以看出,将基于特征点提取的栅格模型应用于人工势场法中时,可以明显减少规划路径的转向次数。另外,传统栅格图中利用人工势场法规划出的路径会频繁经过障碍物栅格的顶点,严重影响AGV的安全运行,这也是人工势场法很少采用栅格法的主要原因,将基于特征点提取的栅格图应用于人工势场法路径规划增加了规划出的路径与障碍物栅格之间的安全距离,提高了AGV运行的安全性,使栅格法更适用于人工势场法的路径规划中。
同时,由图10(b)可以看出,从栅格图中提取出特征栅格,可以有效减少栅格图中局部最优点的个数,从而解决人工势场法中的局部最优问题。在两种栅格模型中人工势场法路径规划的主要数据对比,如表2~4所示。从表中可以看出,新栅格模型中规划出的路径不再频繁经过障碍物的顶点,提高了车辆行驶时的安全性。此外,新的网格模型中规划出的路径在转弯次数和总转弯角度上都小于传统栅格模型中规划出的路径,大大降低了AGV运行时的损耗。
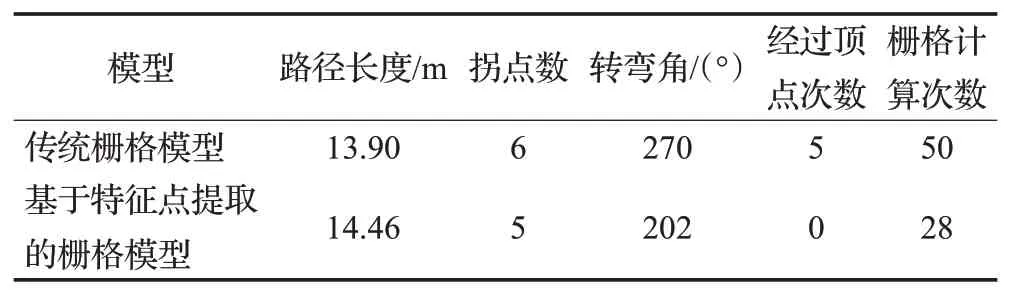
表2 人工势场法在10×10环境模型中规划路径的数据比较Table 2 Data comparison of artificial potential field method in 10×10 environmental model

表3 人工势场法在20×20环境模型中规划路径的数据比较Table 3 Data comparison of artificial potential field method in 20×20 environmental model
从栅格的计算次数上可以看出,在人工势场法应用于新的栅格模型中进行路径规划后,计算量大大减少。此外,可以得出,新栅格图的计算量不再依赖于栅格图的大小,而是取决于环境中障碍物的形状和分布。

表4 人工势场法在30×30环境模型中规划路径的数据比较Table 4 Data comparison of artificial potential field method in 30×30 environmental model
3.2 新栅格法模型应用于A*算法的结果
在三个栅格地图中,起点S的坐标分别为(7.5,8.5),(0.5,0.5)和(16.5,23.5),终点E的坐标分别为(8.5,0.5),(14.5,19.5)和(13.5,8.5)。图10(a)、(b)和(c)上图显示了A*算法在传统栅格法规划出的路径,下图显示了A*算法在新型栅格法规划出的路径,其中黑色实线为规划出的路径,黑色圆圈所在的栅格为路径中包含的栅格,灰色栅格为A*算法搜索的全部栅格。
从图11可以看出,将A*算法应用于特征点提取的栅格建模中,可以减少规划路径上换向节点和非换向节点的数量。此外,还可以减少搜索的栅格数量,从而提高了A*算法的计算效率。

图11 新旧栅格模型中A*算法路径规划的比较Fig.11 Comparison of A*algorithm path planning in new and old grid models
表5~7给出了A*算法在传统栅格模型和新栅格模型中进行路径规划的主要数据比较。从表中可以看出,与A*算法在传统栅格模型下规划的路径相比,新栅格图的A*算法规划的路径更短,转弯次数更少,总转弯角度更小,这样提高了AGV的运行效率,并减少AGV的运行损耗。更重要的是,A*算法的栅格计算数量大大减少,由此加快了A*算法的计算速度。

表5 A*算法在10×10环境模型中规划路径的数据比较Table 5 Data comparison of A*algorithm planning path in 10×10 environment model

表6 A*算法在20×20环境模型中规划路径的数据比较Table 6 Data comparison of A*algorithm planning path in 20×20 environment model
3.3 新栅格法模型应用于蚁群算法的结果
在三个栅格地图中,起点S有坐标(3.5,9.5),(0.5,19.5)和(0.5,8.5),终点E有坐标(2.5,0.5),(18.5,0.5)和(25.5,28.5)。将信息素启发因子α设为1,β设为12。η设为1.55。图12(a)、(b)和(c)上图显示了蚁群算法在传统栅格法规划出的路径,下图显示了蚁群算法在新型栅格法规划出的路径,其中黑色实线为规划路径,黑色圆圈为路径中包含的节点。从图12可以看出,蚁群算法在特征点提取的栅格模型中进行路径规划,减少了规划路径的拐点数量,从而降低了AGV的运行损耗。

图12 新旧栅格模型中蚁群算法路径规划的比较Fig.12 Comparison of ant colony algorithm path planning in new and old grid models

表7 A*算法在30×30环境模型中规划路径的数据比较Table 7 Data comparison of A*algorithm planning path in 30×30 environment model
蚁群算法的迭代曲线如图13(a)、(b)和(c)所示,其中实线为蚁群算法寻找到的当前最短路径,虚线为蚁群算法每一代寻找到的最短路径。

图13 新旧栅格模型中蚁群算法迭代曲线的比较Fig.13 Comparison of iterative curves of ant colony algorithm in new and old grid models
由图可以验证,当蚁群算法在特征点提取的栅格模型中路径规划时,算法的效率显著提高,迭代次数明显减少。算法主要数据的比较如表8~10所示。

表8 蚁群算法在10×10环境模型中规划路径的数据比较Table 8 Data comparison of ant colony algorithm in 10×10 environment model
从表中可以看出,基于特征点提取的蚁群算法规划出的路径具有较少的转弯点和总转弯角度的优点,这样可以减少AGV运行时的损耗,此外,还提高了路径与障碍物之间的平均安全距离。从迭代次数和节点计算次数来看,基于特征点提取的栅格模型排除了原栅格模型中的一些较差解,使得蚁群算法在路径规划时不必考虑这些较差解,从而使路径选择更有目的性,大大缩短了算法的计算时间。

表9 蚁群算法在20×20环境模型中规划路径的数据比较Table 9 Data comparison of ant colony algorithm in 20×20 environment model

表10 蚁群算法在30×30环境模型中规划路径的数据比较Table 10 Data comparison of ant colony algorithm in 30×30 environment model
3.4 实验结果分析
通过仿真结果可以看出,新型栅格法建模对于局部路径规划算法有很好的优化效果。局部路径规划算法只需要由传感器采集环境信息,新型栅格法建模结合传统栅格法中的环境信息表达方式保证了环境信息的完整性,同时新型栅格法建模通过特征提取的方式排除了算法中的较差解。局部路径规划算法中特征栅格节点与周围节点的环境信息变化不大,过多的信息相似解反而会增加算法的运算时间,排除这些解使得算法选择路径更加有目的性。可以看出局部路径规划算法更加适合应用于新型栅格法建模。
4 结语
路径规划算法改进的思想通常是对算法本身进行优化和改进,有时这种改进用于其他路径规划算法时存在局限性。因此,本文提出了一种优化环境建模的新方法,通过提取障碍物的顶点栅格作为特征点来减小算法的搜索范围。该方法可以应用于多种路径规划算法,同时保证一定的优化效果。为了验证这种新栅格模型的适用性,将其应用于人工势场法、A*和蚁群三种不同类型的路径规划算法,并对新方法的性能提升进行了评价。结果表明,新栅格模型适用于不同类型的路径规划算法,并且可以解决这些算法存在的局部最优、搜索速度慢和迭代次数多等问题,从而提高了这些算法的性能。特征点提取下的栅格模型具有很强的适用性,并且可以对不同的算法做出优化,为优化环境建模方法提供了一种新的思路。

