海底管道敷设过程的海底拖管强度分析
王佐强,章仲怡,唐友刚,李 焱
1.中海油能源发展股份有限公司清洁能源安装分公司,天津 300452
2.天津大学建筑工程学院,天津 300350
滩海水域的海底管道敷设,其关键技术是如何将海管运输到管道布设的路由。采用的方法包括浮托运输方法,即管道上绑扎浮筒,管道在水面上处于漂浮状态时拖拉,该方法受风、浪、流影响较大,不适合风、浪、流较大海域拖管[1-2]。风、浪、流较大的海域,通常采用底拖法拖管,拖管时管道紧贴着海底,由一般的拖轮或牵引绞车船和一条长的拖缆(钢缆)将管道拖进,其优点是受波浪、涌浪等的作用较小,就位轨迹易控制[1-2]。虎蕾[3]等总结了底拖管的风险,包括改变路由、较大摩擦力及损伤海底管道。金志英等[4]采用基于有限元法的商业软件,计算分析海管下水过程的管道变形和应力分布。传统的底拖管海底管道和拖管头均在水下泥面附近,拖管时管道全部与泥面接触,拖带管道阻力大,需要的拖索长[5]。本项目对传统的底拖管施工方法进行了改进,即把拖管头提升到泥面适当高度进行拖管,从而减少拖管与泥面的接触,而钢缆不再与泥面摩擦。对于这种改进的底拖管法,研究了基于解析解的计算分析方法,编制了计算机程序,可以计算底拖过程管道的应力和变形。
1 底拖法的改进
图1为改进的底拖法拖航示意,即将管道与拖管头的联结部分提升一定高度进行拖管。这种方法具备的优点是:其一,由于钢缆不再与海底接触,减少了钢缆的磨损和拖地时的摩擦力;其二,缩短了钢缆的长度,有利于对管道的控制、定位和位置的调整;管道在拖拉时,底部有升离海床的趋势,摩擦力有所降低,牵引力减小。

图1 改进的底拖法施工示意
2 改进底拖法施工的管道强度计算方法
底拖牵引拖管过程中,管道受到的载荷主要包括:管道自身的负浮力、海底的摩擦阻力、拖船的牵引力。管道的受力模型建立在如下假设基础上:管道底部与海底全部接触,各处都没有架空段,其以均匀的重量作用于海底,管道与海底土的摩擦系数均匀一致。管道处于海底时,其负浮力只是作为管道的压力产生海底摩擦力,摩擦阻力分为轴向和横向的,轴向的摩擦力与拖船牵引力相平衡,横向的摩擦力与海底海流的拖曳力反向。考虑到通常底拖施工选择在海底海流流速较小的情况下进行,海底海流产生的横向拖曳力不足以克服海底的摩擦力,故分析时忽略了海底海流的横向拖曳力。
对图1所示的管道进行分析分为三个部分:第一,确定管道的参数如抬升高度Y;第二,计算钢缆牵引拉力T及管道最大弯曲应力;第三,计算管道海底摩擦阻力以及轴向应力。
2.1 钢缆的牵引拉力计算
图1所示的钢缆,其牵引拉力计算主要应用标准悬链线方程[6]来进行计算。拖管钢缆上任意点的坐标为:

式中:z为钢缆上任一点到海底的高度,m;x为在图1坐标系下钢缆上任一点到原点的水平距离,m;Th为水平拖力,N;w为单位长度重力,N/m。
拖缆上任一点到拖缆起始点的缆长为:

式中:s为到钢缆上任一点的拖缆长度,m。
拖缆任意点处的表观张力:

式中:T为钢缆总表观拖力,N;T0为初始牵引力,N;ϕ0为初始缆索与水平夹角,(°)。
拖缆任意点处的实际张力:

式中:Tt为钢缆上任意点处的拖力,N;h为水深,m。
2.2 离底管段的强度计算
对于图1中②~③悬垂管段的计算,由于滩海水域离底高度Y相对于管道拖底的长度非常小,故此部分计算主要是应用弹性梁理论和微小挠度理论[5,7]进行推导。将图1中②~③悬垂管段模拟为如图2所示的一段梁,考虑小挠度理论可得。
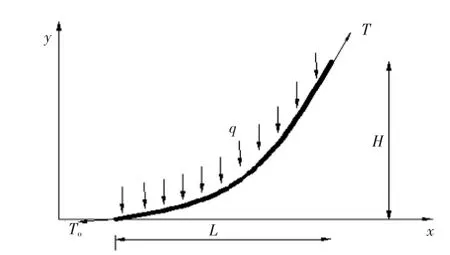
图2 管道悬垂段的受力模型
则根据弹性梁理论,可得管道基本弯曲微分方程为:

式中:q为管道的负浮力,N/m;EI为管道的抗弯刚度,N·m2;T0为管道拖底部分的摩擦阻力,N。
初值边界条件为:

式中:y′和y″为表示对x求一阶和二阶导数;H为图2中船上拖点到海底的高度,m。
由边界条件求解微分方程得到:
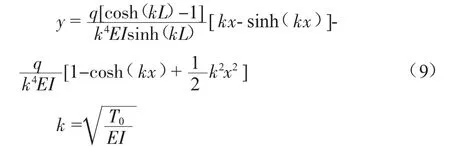
式中:L为未知数,不同的离底高度有不同的L值,其中T0是L的函数。
根据微小挠度理论,T0由式(10)得到:

式中:u为海底摩擦力系数;LP为所拖管道的长度,m。
通过y(L)=H,在给定H情况下将L的初值代入式(10),计算T0(L),并将T0(L) 代入式(9),得y值,并与H比较,如此迭代求解L值,就可以得到管道悬空部分的变形方程y(x)。悬垂段管道的弯矩由式(11)计算:

由式(11)求得此管段的弯矩,并进而求得弯曲应力。
基于以上解析计算方法,采用vb.net编写计算机程序[8],计算在拖管过程中拖管离地的高度,计算拖缆构型,计算悬空段管道弯矩。
3 算例及计算结果
计算如下的管道实例。管道尺寸:外管ϕ325mm×6 mm,内管ϕ273 mm×8 mm;管道负浮力G2=16.09 kg/m;管道总长500 m;屈服应力358.6 MPa。拖缆选用ϕ43 mm的圆截面钢缆;水深5 m;海底摩擦力系数为0.6;拖管速度2 kn。采用本文编制的程序计算,并使用vb.net绘图工具绘制管道的变形图、弯矩图。
3.1 拖管头离泥面1.0 m
计算得到图3所示的管道悬垂段变形。经计算,当H=1.0 mm时,L=43.859 6 m,此时T0=43 154 N,T=4 311 N,k=0.051 8;拖管钢缆最大牵引力为:Tg=43 755 N,所需拖缆的长度至少为57 m。悬垂段管道的弯矩由式(4)计算得出,弯矩见图4。其中弯矩最大值为24 540 N·m,悬垂段管道的最大轴向拉应力为54.04 MPa。

图3 拖管头离泥面1.0 m时悬垂段变形

图4 拖管头离泥面1 m时悬垂段弯矩
3.2 拖管头离泥面2.0 m
计算得到如图5所示管道变形图,当H=2.0mm时,L=54.1974m,此时T0=42173N,T=42488N,k=0.051 2;拖管钢缆最大牵引力:Tg=42 821 N;所需拖缆的长度至少为49 m。悬垂段管道的弯矩由式(9)计算得出,如图6所示。其中弯矩最大值为31 848 N·m,悬垂段管道的最大轴向拉应力为69.53 MPa。

图5 拖管头离泥面2.0 m时悬垂段变形

图6 拖管头离泥面2.0 m时悬垂段弯矩
3.3 拖管头离泥面2.8 m
经计算得到如图7所示管道变形图。当H=2.8 m时,L=60.305 4 m,此时T0=41 593 N,T=42 034 N,k=0.050 9;拖管钢缆最大牵引力为Tg=42 278 N;所需拖缆的长度至少为41 m。悬垂段管道的弯矩由式(9)计算得出,如图8所示。弯矩最大值为35 801 N·m,悬垂段管道的最大轴向拉应力为77.92 MPa。

图7 拖管头离泥面2.8 m时悬垂段变形

图8 拖管头离泥面2.8 m时悬垂段弯矩
以上三种情况及与传统底拖法结果对比见表1。
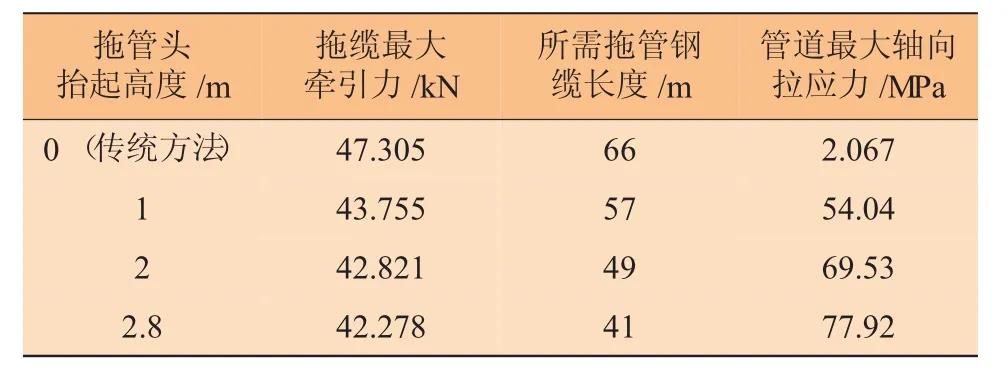
表1 拖管头离泥面三种高度工况计算结果与传统底拖法的对比
4 结论
本文针对滩海浅水海域底拖海底管道施工,改进了传统的施工方法,建立了底拖法管道强度计算的解析方法,编制了计算机程序,得到如下主要结论:第一,海底拖管时抬高拖管头可以降低拖带阻力,牵引力也可减小;第二,在拖管头抬升过程中,拖管悬空段最大的等效应力发生在悬垂的弯曲段,且随抬升高度增加而逐渐增加;第三,海底拖管抬高拖管头,可缩短拖管钢缆的长度,进而可以降低索具费用;第四,所建立的管道强度计算解析方法和编制的程序均可行,具有一定的工程实用价值。

