面向混合数据的代价敏感三支决策边界域分类方法

周阳阳，钱文彬,2，王映龙，彭莉莎，曾武序

（1.江西农业大学 计算机与信息工程学院，江西 南昌 330045;2.江西农业大学 软件学院，江西 南昌 330045;3.南京大学 工程管理学院，江苏 南京 210046）

三支决策是加拿大学者Yao[1-2]提出的一种“化繁为简”决策理论，它从粒计算视角将论域划分为三个互不相交的论域子空间，并对其分别采取不同的应对策略，这种分而治之的思想，可有效提高决策准确度，降低误分类代价。三支决策理论模拟人类认知、学习和决策的过程，可处理决策过程中出现的不确定性问题。近年来，三支决策理论引起了许多研究者的关注，已成为了粒计算和知识发现领域中的一个重要研究方向。目前，三支决策在众多应用领域中得到广泛的应用，如人脸识别[3]、推荐系统[4-5]、决策系统[6]和邮件过滤[7]等；为了处理复杂的应用场景，提出了不同的计算模型，如序贯三支决策[3,8]、优化三支决策[9]、前景三支决策[10]、三支模糊集[11]和三支约简[12]等。

在实际应用中，代价是影响三支决策划分的重要因素之一。代价敏感学习能够有效缓解分类过程中的数据不平衡问题，其主要作用是处理决策过程和结果产生的各类代价问题。代价敏感学习主要研究两种代价：误分类代价（结果代价）和测试代价，两者互相关联，呈负相关。如在医疗诊断中，患者想要获得更高的诊断准确率（即决策代价越低），就需要做更多的检查（即测试代价越高）。由于代价是数据的内在特征，将其与知识发现结合会使得问题更具有普适性，目前，代价敏感学习已经应用到现实生活中的许多领域，如：人脸识别[13]、价格预测[14]和客户信用评价[15]等。

因此，基于代价敏感的三支决策算法与模型引起了许多学者的关注和研究，已取得重要的研究成果。Fang 等[8]将信息粒度纳入决策分析过程，同时考虑决策过程和决策结果的代价，分别设计了两种不同的算法以最小化决策过程和决策结果代价。Fang 等[16]提出了一种三支决策和可分辨矩阵的框架，在此框架下分别设计了基于删除和增加的代价敏感近似属性约简算法。Jia 等[17]构造了一种可以直接应用于传统的代价敏感学习问题的三支决策模型，在此基础上，提出基于多类三支决策模型的多阶段代价敏感学习方法。Li等[18]为从输入图像中顺序提取分层粒度结构，提出了一种基于DNN 的顺序粒度特征提取方法，在此基础上，提出一种代价敏感的序贯三支决策模型。Yang 等[19]考虑了用户需求， 提出一种基于模糊粗糙集的序贯三支决策模型的优化机制，用来实现对代价敏感的最优粒度选择。Ma 等[20]定义了三支特定类的最低代价约简，分别设计了基于添加−删除策略和删除策略来构建特定类的最小代价约简算法。以上算法与模型能够最小化结果代价或过程代价。而在许多应用领域中往往需要从代价敏感视角来分析三支决策边界域样本，目前三支决策的研究对象多为单一性数据的决策系统，对于混合数据边界域样本处理的研究相对较少。

为此，本文提出了一种面向混合数据的代价敏感三支决策边界域分类方法。首先，基于正域约简，提出了面向混合数据的属性约简模型；然后，提出了一种基于代价敏感的三支决策边界域样本处理方法，在贝叶斯最小风险的基础上构造误分类代价公式，划分边界域中的对象。最后，对UCI 上的10个数据集进行实验，结果表明该方法能够降低误分类代价，而且能较准确地划分边界域中的对象；这为三支决策的边界域样本处理提供了一种可借鉴的方法。

1 基本知识

1.1 邻域粗糙集

在粗糙集理论[21]中，给定一个四元组决策系统：

其中U={x1,x2,···,xn}表示有限非空的对象全集，称为论域或者对象空间；At表示有限非空的属性全集，由条件属性和决策属性共同组成；C={a1,a2,···,an}表示有限非空的条件属性全集；D表示决策属性；Va表示a∈C的属性值集；Ia|U×At→V是一个信息函数，能给每个对象的每个属性赋值，即Ia(x)→Va。

定义1[22]给定混合邻域决策系统DN={U,FD∪FC,D,Va,Ia,δ}，距离度量函数ΔN:U×U，给定属性子集B⊆C和邻域参数δ，则对象x和y基于B的邻域关系为

式中：FD为离散属性集合；FC为连续属性集合；δ是邻域参数。

1.2 三支决策粗糙集

三支决策粗糙集[23]通过2个状态集和3个动作集来描述其决策过程。其中，状态集S={X,¬X}分别表示对象属于概念X和不属于概念X，动作集A={aP,aB,aN}表示对于不同状态分别采取接受、延迟和拒绝3 种不同的动作。由于采取不同动作会产生不同的损失，记λPP、λBP、λNP表示当x∈X时，分别采取动作aP、aB和aN产生的风险损失值；同样地，记λPN、λBN、λNN表示当x∈¬X时，分别采取动作aP、aB和aN产生的风险损失值；损失之间的关系满足：λPP<λBP<λNP，λNN<λBN<λPN。在实际应用中，这些损失值通过专家的经验获取。

定义2[1]在决策系统DS={U,C∪D,Va,Ia}中，令X为论域U基于决策属性D的划分，α 和β为三支决策的阈值，P(X|[x])表示对象x的条件概率，对于∀x∈U，根据贝叶斯决策过程，计算得到最小成本准则的三支决策规则：

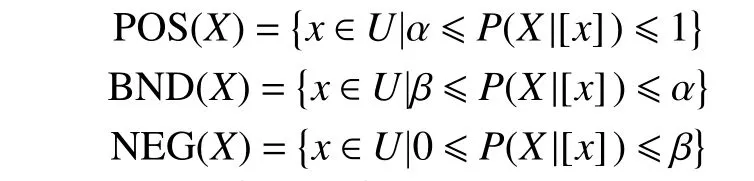
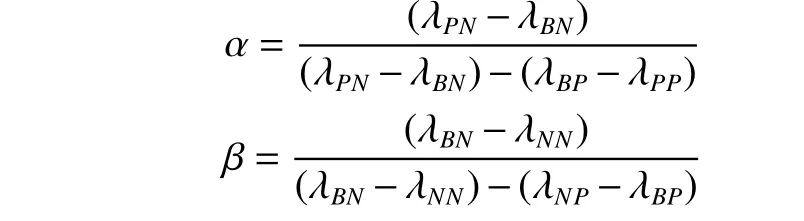
其中，正域POS(X)、负域NEG(X)和边界域BND(X)分别对应三支决策规则中的接受、拒绝和不承诺规则，且满足：POS(X)∪BND(X)∪ N EG(X)=X；仅当X=U时，P OS(X)∪BND(X)∪NEG(X)=U。

1.3 代价敏感学习

代价敏感学习主要研究误分类代价和测试代价，由于本文中考虑了其误分类代价，误分类代价表示对对象错误划分后的一种惩罚。用Ck×k表示误分类代价矩阵，其中k表示k分类问题。为方便理解，以二分类代价矩阵为例；其中c11表示将类别为1 的对象划分到类别1 中，因此c11的值为0，同理c22的值也为0；c12表示将类别为1 的对象划分到类别2 中，此时属于误分类，在划分中需付出惩罚代价，因此c12>0，同理c21>0。

2 基于正域约简的代价敏感三支决策边界域分类方法

2.1 面向混合邻域决策系统的正域约简

由于基于三支决策的粒计算方法大多是处理连续型数据或离散型数据等单一型数据，但是在现实生活的应用领域中数据类型通常是既含有连续型数据又含有离散型数据的混合数据，为此需对混合数据的三支决策模型展开研究。

定义3给定混合邻域决策系统DN={U,FD∪FC,D,Va,Ia,δ}，Va(x)表示对象x在属性a上的属性值：

对于∀x,y∈U,∀a∈FD，则x和y基于FD的距离为

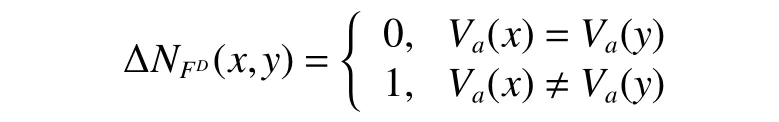
对于∀x,y ∈U,∀a ∈FC，则x 和y基于 FC的距离为

其中，当p=1时，ΔNFC(x,y)为曼哈顿距离；当p=2时，ΔNFC(x,y)为欧氏距离；当p→∞时，ΔNFC(x,y)为切比雪夫距离。

定义4给定混合邻域决策系统FC,D,Va,Ia,δ}，令Di为论域U基于决策属性D的划分，则混合邻域决策系统的上下近似表示为：

通过上下近似集，可知特征子集B上的正域如下：

定义5给定混合邻域决策系统DN={U,FD∪FC,D,Va,Ia,δ}，令属性ai∈C，则混合邻域决策系统中基于三支决策的核属性集定义为：

以表1 为例，给出一个混合邻域决策系统，其中，U={x1,x2,···,x10}为对象集，C={a1,a2,···,a6}为条件属性集,决策类U/D={D1,D2}，分别为D1={x1,x3,x5,x6,x7,x9}，D2={x2,x4,x8,x10}。

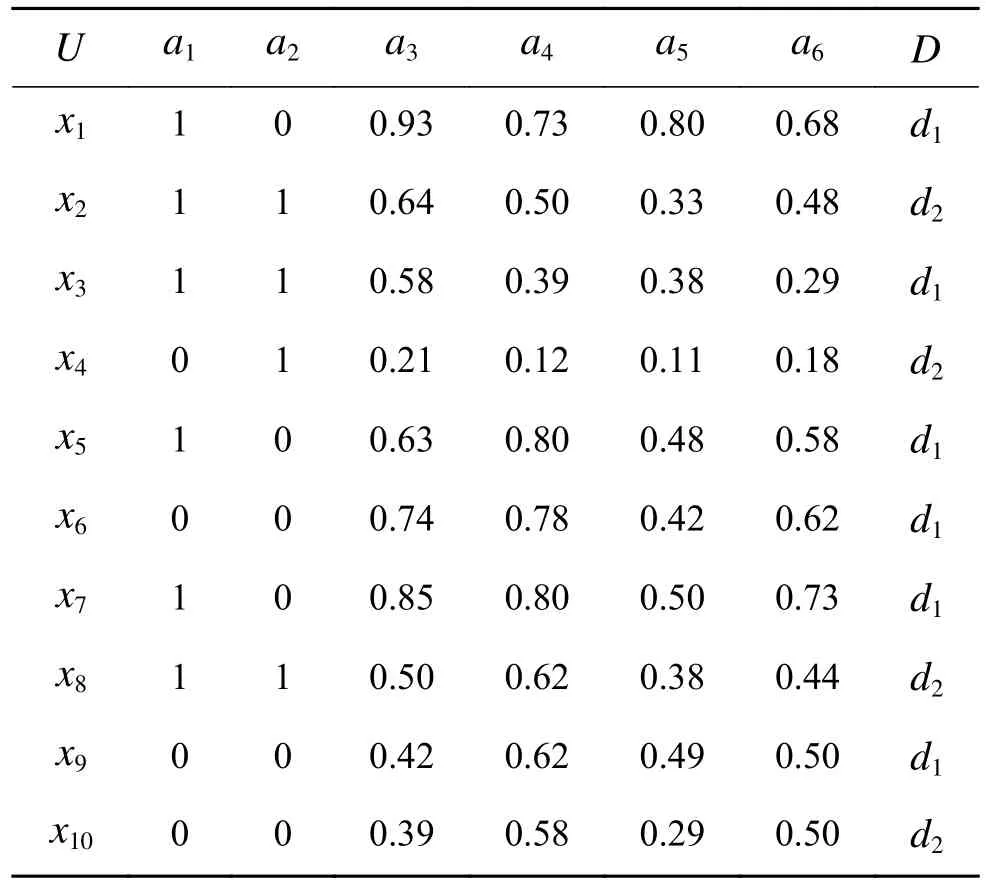
表1 混合邻域决策系统DNTable1 Hybrid neighborhood decision system DN

根据定义5 可计算出混合邻域决策系统的核属性集，具体的计算过程为：首先，根据定义3，利用p=2时的欧氏距离计算全体对象的混合邻域粒度，再根据定义5 计算出POSC(D)={x1,x4,x5,x6,x7}，同理可计算出POSC−{a1}(D)={x1,x4,x5,x6,x7},因为POSC(D)=POSC−{a1}(D),所以属性a1∉ C ORE(C)，同理可求出{a2,a3,a5,a6}∉CORE(C),只有属性a4∈CORE(C)。由此可知核属性集为CORE(C)={a4}。下面将在此基础上，提出了代价敏感下的三支决策边界域分类方法。

2.2 基于核属性集的代价敏感三支决策边界域分类方法

定义6给定混合邻域决策系统DN={U,FD∪FC,D,Va,Ia,δ}，设属性子集B⊆C，α 和β为三支决策的阈值，Di表 示不同的决策属性，则不同属性子集下的三支决策规则定义为：

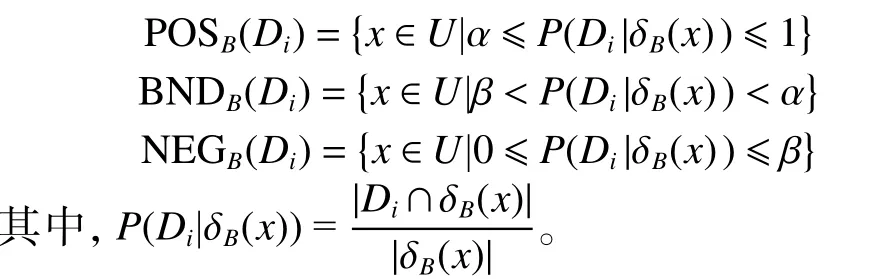
以表1 为例，可给出混合邻域决策系统代价矩阵，如表2 所示。结合定义2 和表2，可求出三支决策的阈值α=7/9,β=1/3。

表2 误分类代价矩阵Table2 Misclassification cost matrix

令B=CORE(C)={a4},根据定义3 可计算出核属性子集B下的对象之间的邻域粒度；再根据定义6 计算出核属性集下决策类D1的的正域、负域和边界域，具体的计算过程为：由定义3 可计算出核属性集B下x1的邻域粒度δB(x1)= {x1,x2,x5,x6,x7,x8,x9,x10},由此求出x1的条件概率P(D1|δB(x1))=5/8<α，所以x1∈BNDB(D1)，同理{x2,x4,x5,x6,x7,x8,x9,x10}∈BNDB(D1)，即BNDB(D1)={x1,x2,x4,x5,x6,x7,x8,x9,x10}。通过相同的计算可求出：

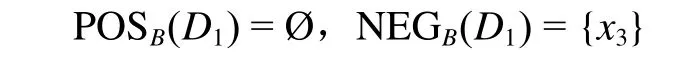
定义7在混合邻域决策系统DN=U,FD∪FC,D,Va,Ia,δ}中，Di为论域U基于决策属性D的划分，给定属性子集B⊆C，为了简化公式，用CPr和(1−CP)r分别代替，对于∀xj∈BNDB(Di)，样本简化后的误分类代价计算公式如下：

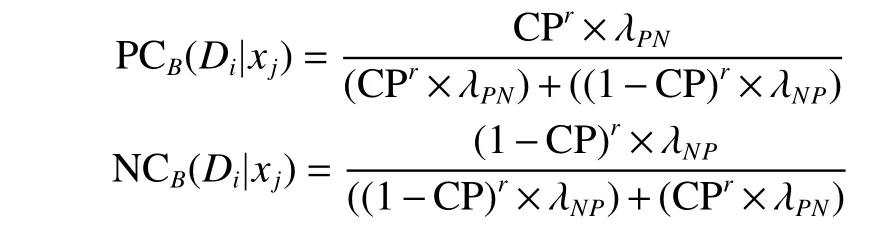
其中，PCB(Di|x)表示在决策类Di下将对象x划分到正域产生的误分类代价，同理，NCB(Di|x)表示在决策类Di下将对象x划分到负域产生的误分类代价。λNP和λPN是代价矩阵中的风险损失值，P(Di|δB(x))表示在决策类Di下对象x的条件概率。

性质1在混合邻域决策系统DN={U,FD∪FC,D,Va,Ia,δ}中，Di是对决策属性D的划分，假设属性子集B⊆C，对于∀x∈BNDB(Di)，可得出如下推论：

1)如果PCB(Di|x)>NCB(Di|x)，则x∈NEGB(Di)；

2) 如果PCB(Di|x)≤NCB(Di|x)，则x∈POSB(Di)。

以表1 为例，令B=Core(C)={a4}，已知D1={x1,x3,x5,x6,x7,x9} 和BNDB(D1)={x1,x2,x4,x5,x6,x7,x8,x9,x10}，根据定义7 和性质1 可将边界域中的对象划分到正域和负域，具体的计算过程如下：

对于∀x∈BNDB(D1)，根据定义7 可求出划分对象x1产生的两种误分类代价PCB(D1|x1)=6/11，NCB(D1|x1)=5/11，因为PCB(D1|x1)>NCB(D1|x1)，所以x1∈NEGB(D1)，同理可得{x2,x4,x6,x8,x9,x10}∈NEGB(D1)和{x5,x7}∈POSB(D1)。由此可知，该混合邻域决策系统的正域为POSB(D1)={x5,x7}，负域为NEGB(D1)={x1,x2,x3,x4,x6,x8,x9,x10}。

3 算法描述及复杂度分析

针对混合邻域决策系统，为了有效划分其三支决策边界域中的对象，本文提出了一种面向混合数据的代价敏感三支决策边界域分类方法，该算法主要分为三个部分。首先，针对混合邻域决策系统中的数据，通过混合邻域计算公式计算每个对象的混合邻域粒度，得到混合邻域决策表的正域对象集合，由此基于启发式策略计算核属性集。其次，在此基础上，计算混合邻域决策表中每个对象的邻域粒度，从而计算出每个对象属于不同决策类的条件概率，利用三支决策规则将对象分别划分到不同决策类的正域、边界域和负域中；最后，针对边界域中的对象，分别计算其划分到正域和负域所产生的误分类代价，通过比较这两种代价的大小，将边界域中的对象划分到正域或负域中，为此，算法的流程图1 所示。

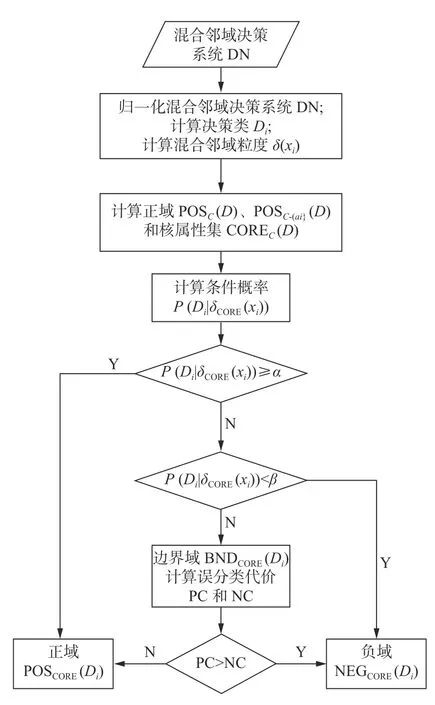
图1 算法流程图Fig.1 The flowchart of algorithm

算法面向混合数据的代价敏感三支决策边界域分类方法

①若α≤P(Di|δCOREC(D)(x))≤1，则将对象x划分到决策类Di的正域 P OSCOREC(Di)；

②否则，若0≤P(Di|δCOREC(D)(x))≤β，则将对象x划分到决策类Di的负域 N EGCOREC(Di)；

③否则将对象x划分到决策类Di的边界域BNDCOREC(Di)；

8）对于∀xb∈BNDCOREC(Di)计算PCCOREC(Di|xj)和NCCOREC(Di|xj)：

①若满足PCCOREC(Di|xj)>NCCOREC(Di|xj)，则将对象xj划分到决策类Di的负域 N EGCOREC(Di)；

②否则将对象xb划分到决策类Di的正域POSCOREC(Di)；

9）输出划分结果正域POSCOREC(Di)，负域NEGCOREC(Di)。//算法结束。

算法时间复杂度分析：

1）算法的时间复杂度为O(|U||C|)；2）划分决策类所需的时间复杂度为O(|U|)；3）在属性全集下，通过混合邻域计算公式得出每个对象的混合邻域粒度，其时间复杂度为O(|U|2|C|)；4）计算正域对象的时间复杂度为O(|U|)；5）计算核属性集的时间复杂度为O(|U|2|C|)；6）在核属性集CORE下，计算每个对象的混合邻域粒度，其时间复杂度为O(|U|2|COREC(Di)|)；7）计算各决策类正域、边界域和负域，其时间复杂度为O(|U|)；8）结合代价敏感划分边界域中的对象，其时间复杂度为O(|BNDCOREC(Di)|)。综上所述，算法最坏情况下的时间复杂度是O(|U|2|C|)；由于存储空间主要用于存放数据，因此算法的空间复杂度为O(|U||C|)。

4 实验比较与分析

为了验证本文方法对边界域对象划分的可行性和有效性，实验从UCI 中选取了10个混合数据集进行实验测试与分析；选用分类准确率、权衡因子、误分类损失和时间作为评价指标，对实验结果进行对比与分析。

4.1 数据集与实验设置

为了更好地说明所提出算法的普适性，本文根据数据集的来源和规模两个方面，从国际公开的机器学习UCI 数据库中选取了10个数据集进行实验结果的对比和分析，数据集的信息描述如表3 所示。表中Speaker Accent 和Ionosphere 数据集中包含连续型数据，Phishing Websites 和Student Evaluation 数据集中包含离散型数据；其余数据集均包含连续型和离散型数据；这些数据集来自欺诈分析、医学诊断、信号处理和教育评价等应用领域。 同时为了消除量纲的影响，对所有数据集中的连续型数据进行归一化处理。本次实验的运行环境为：Win10,Intel(R)Core(TM),i5-6 500 CPU @ 3.20 GHz 3.19 GHz 和8 GB 内存，用Python 编程语言实现算法设计。

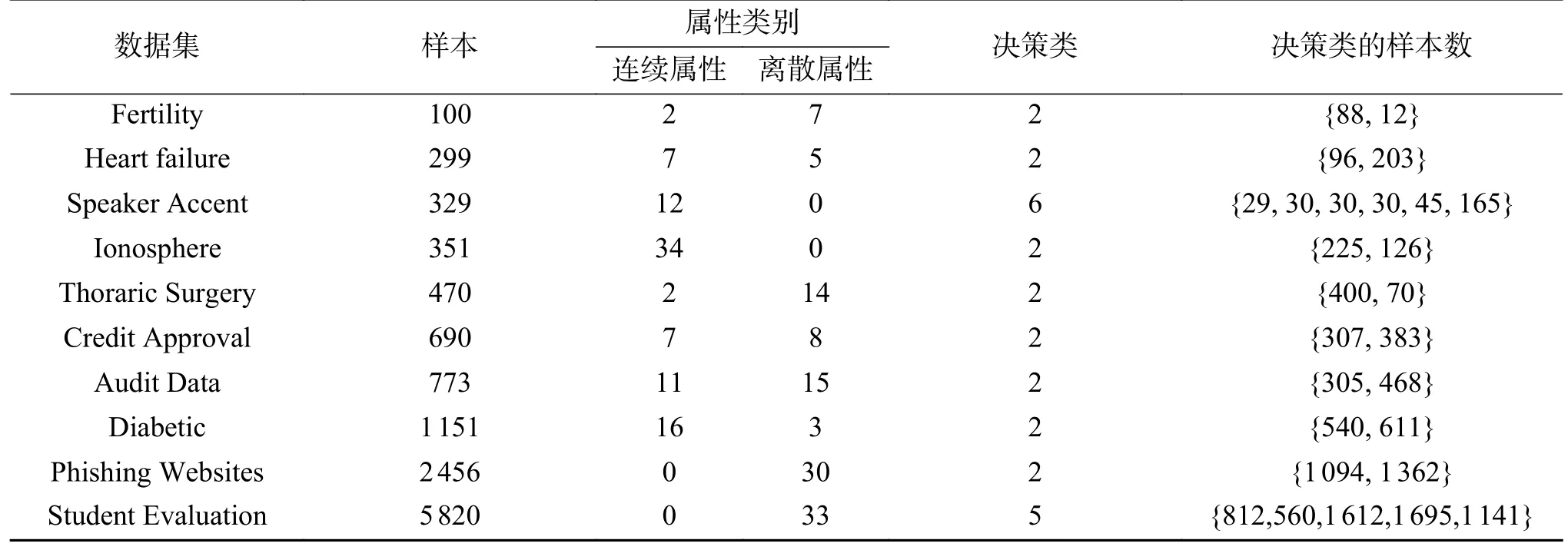
表3 数据集的基本信息Table3 Basic information of the data set

4.2 评价指标

实验将从准确率、权衡因子、误分类损失和运行时间4 种度量指标[24]对划分结果进行分析，定义如下：

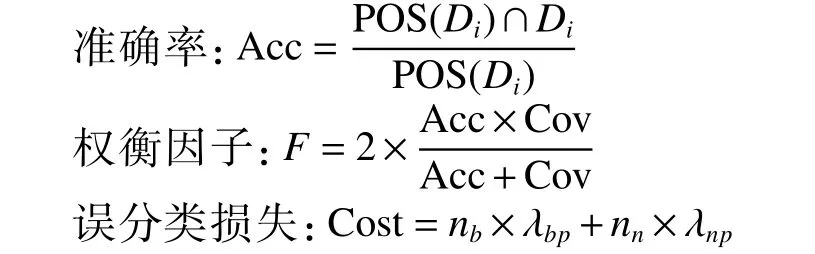
式中：POS(Di)和Di表示正域和决策类，nb和nn分别表示边界域、负域中的对象个数；λbp和λnp分别表示将属于某一决策类的对象错误划分到该类别的边界域和负域中产生的损失；由于本文算法的输出只包含正域和负域，因此Cov=1。本实验的风险损失参数为λbp=0.3，λnp=0.7。

4.3 实验结果与分析

4.3.1 参数 λPN和λNP对划分结果的影响

在混合邻域决策系统中，参数 λPN和λNP通过影响阈值对(α,β)的大小来影响三支决策的划分。因此，为了详细分析参数 λPN和λNP的值对划分准确度的影响。本小节中，为了一般性，从上述数据集中选取6个作为代表进行实验分析，分别将λPN和λNP的值从3 到10，且每次步长变化1 进行实验。实验结果如图2 所示。

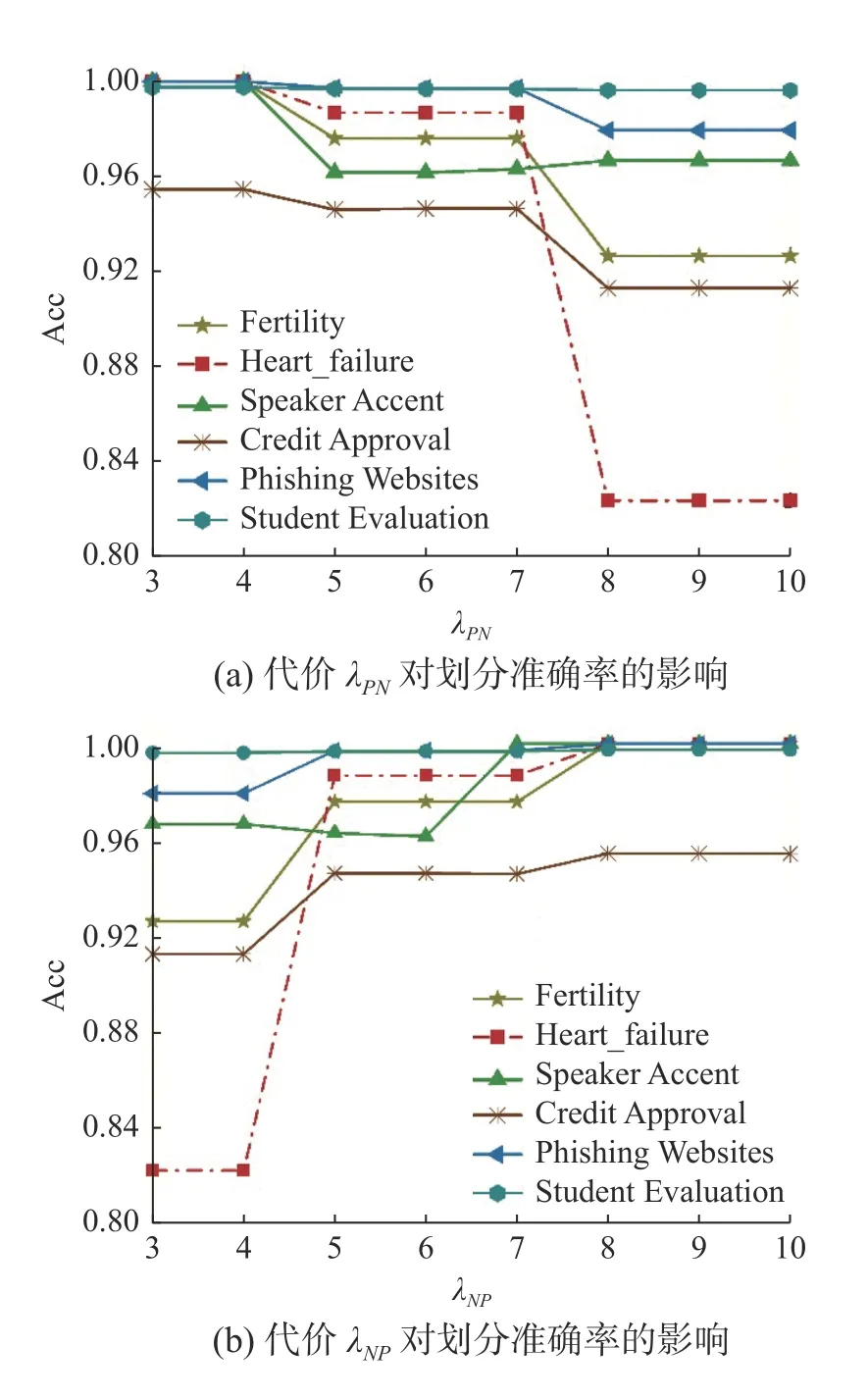
图2 参数λPN和λNP对准确率的影响Fig.2 Influence of parameters λPNand λNPon the accur acy

在图2(a) 中，当λPN的取值区间在[4,5]时，Credit Approval 等5个数据集的准确率随代价的增加而下降，且变化趋势较为平缓；当 λPN的取值区间在[7,8]时，这些数据集的准确率随代价的增加而下降，且变化趋势较为显著。在图2(b) 中，当 λNP的取值区间在[4,5]时，Credit Approval 等5个数据集的准确率随代价的增加而上升，且变化趋势较为显著；当 λNP的取值在[6,7]区间时，数据集Speaker Accent 的准确率随代价的增加而升高，进而达到平稳状态；当λNP的取值在[7,8]时，Credit Approval 等个5 数据集的准确率随代价的增加而升高，且变化趋势较为平缓；当代价 λPN和λNP的取值在[8,10]时，准确率达到平稳状态，所有数据集的准确率不再随着代价的变化而变化。

综上所述，从整体上看，代价 λPN和λNP对分类准确度的影响呈负相关，数据集的准确率随着代价 λPN的增加，呈现出整体下降的趋势；而随着代价λNP的增加，整体呈现上升的趋势。从局部上看，当代价的取值在[4,5]和[7,8]这两个区间时，数据集的准确率随着代价的增加而发生变化，当代价的取值在其他区间时，数据集的准确率趋于稳定的状态。由此，在实际的决策过程中，可结合上述分析的结论，并根据数据集的分布和代价敏感学习构造合适的代价矩阵。

4.3.2 本文模型与不同三支决策模型的对比分析

本节主要分析不同三支决策模型对分类性能的影响，表4～7 给出了3 种粗糙集模型下准确率Acc、权衡因子F、误分类损失Cost 和运行时间Time 的实验结果。其中，NCTM (neighborhood rough set based cost-sensitive three-way decision boundary region processing model)是基于邻域粗糙集[25]设计考虑了代价敏感的三支决策边界域处理模型，PCTM (pawlak rough set based cost-sensitive three-way decision boundary region processing model)是基于经典粗糙集[22]设计考虑了代价敏感的三支决策边界域处理模型，MCTM (mixedneighborhood rough set based cost-sensitive three-way decision boundary region processing model)代表本文基于混合邻域粗糙集的代价敏感三支决策边界域处理模型。在PCTM 模型中对数据集进行离散化预处理，在NCTM 和MCTM 模型中对数据集进行了归一化预处理，另外，为了使距离处于同一量纲下，在NCTM 模型中采取平均距离度量，同时Acc、F、Cost 和Time 的值均为数据集所有决策类的平均值。实验结果如表4～7 所示，其中，符号 ↑表示度量指标的值越大越好，符号 ↓表示度量指标的值越小越好，加粗字体表示算法在所对应的数据集上的最优值。

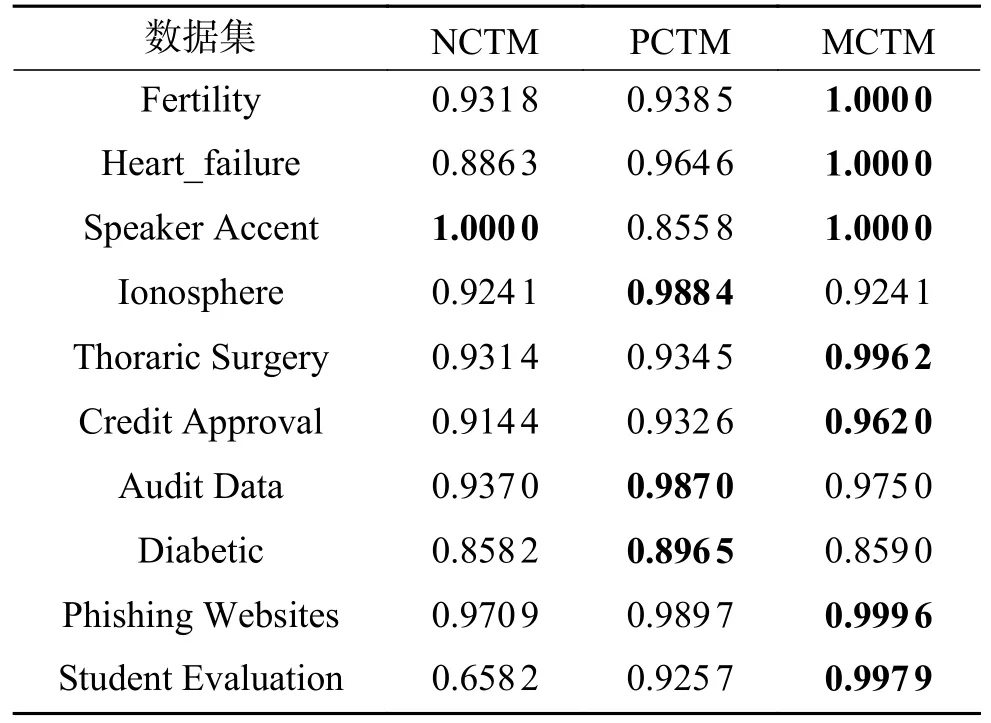
表4 三种粗糙集模型的准确率Acc(↑)对比Table4 Comparison of accuracy Acc(↑)under three kinds of rough set models

如表4 所示，使用本文模型的分类准确率高于其他2 种模型，例如，其在数据集Credit Approval 上的准确率比NCTM 和PCTM 模型分别提高了4.8%和2.9%，由于MCTM 能够针对不同的数据类型采取不同的分类方法，且具有更低的错误率，因此其划分准确率能整体上高于NCTM 和PCTM。此外，在数据集Ionosphere 上，PCTM 模型的优势更加明显，而在数据集Speaker Accent上，本文模型和NCTM 模型的准确率相同，由此可知，本文模型能有效地提高分类准确率，且在数据集上整体表现良好。

如表5 所示，对权衡因子而言，由其度量公式可知，权衡因子由准确率和覆盖率共同决定，由于本文中的三支决策最终转换成二支决策，因此覆盖率Cov=1，在本文中权衡因子F很大程度上取决于准确率Acc 的值。对比表4 和表5 的实验结果可知，权衡因子F的值略高于准确率Acc 的值 ，但是整体上的变化趋势和Acc 相同。

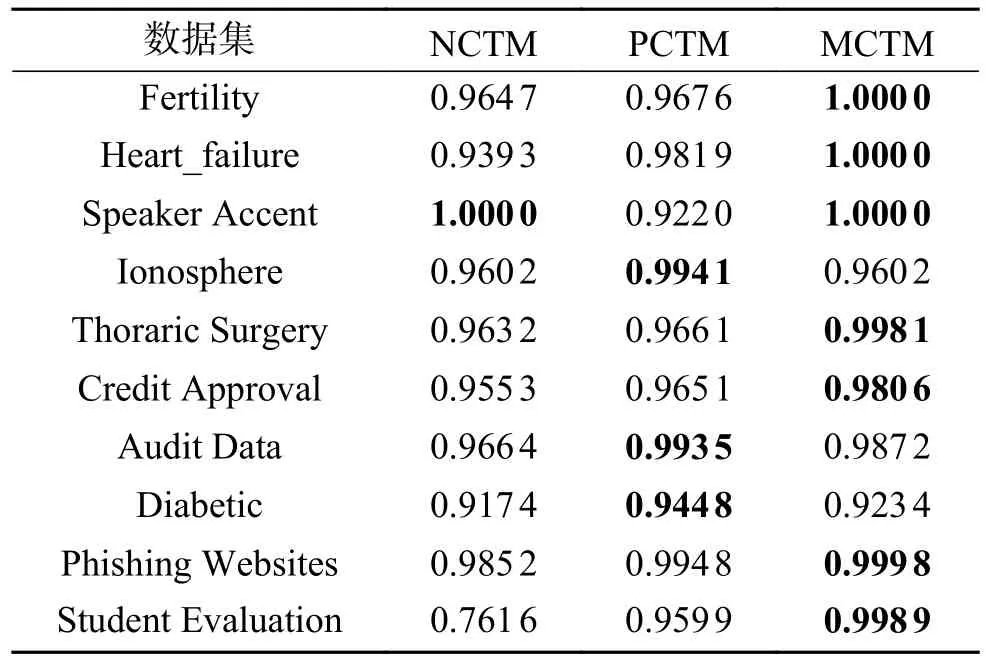
表5 3 种粗糙集模型的权衡因子F(↑)对比Table5 Comparison of trade-off factorF(↑)under three kinds of rough set models

如表6 所示，使用本文模型的误分类损失整体上明显低于其他2 种模型，例如，在数据集Student Evaluation 中，本文模型的误分类损失比NCTM 和PCTM 分别降低了478.1 和287.0。从不同的模型角度分析，针对混合邻域决策系统，PCTM对划分的要求较为苛刻，而NCTM 对划分的要求较于放松，容错率低，导致划分错误率提高；本文模型MCTM 可灵活应用于不同类型的决策系统，容错率高，所以具有更低的误分类代价。

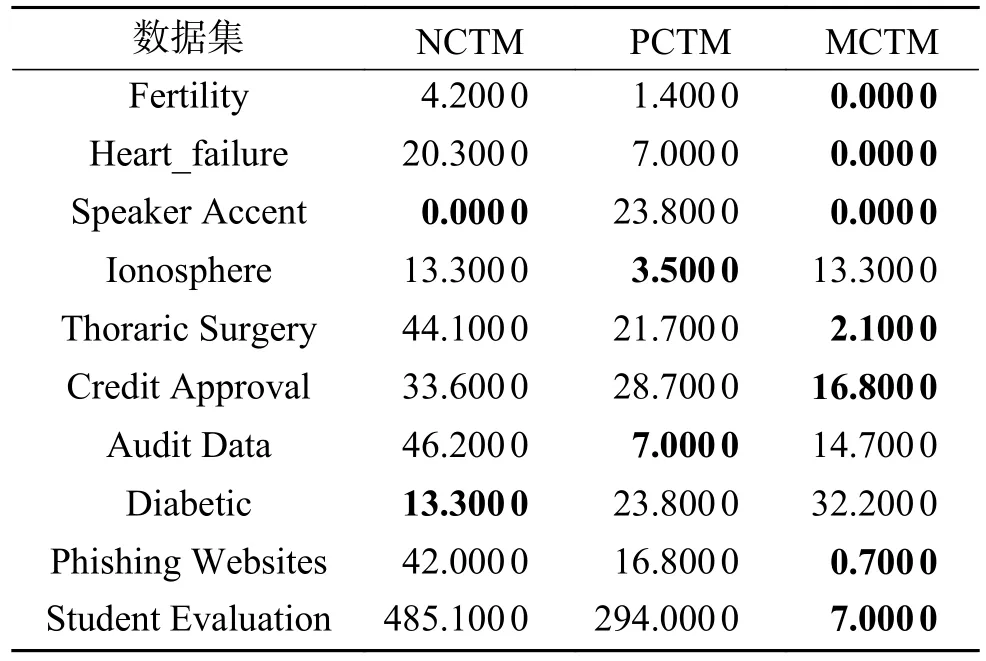
表6 3 种粗糙集模型的误分类损失Cost (↓)对比Table6 Comparison of misclassification loss Cost (↓)under three kinds of rough set models

如表7 所示，从整体上看，3 种粗糙集粒计算模型所消耗的时间较少且随着数据规模的增大而增多；从部分上看，NCTM 模型耗时相对较长，主要是由于NCTM 是用邻域关系计算邻域类，每两个对象之间都要计算，导致其时间复杂度较高。而PCTM 模型和MCTM 模型在耗时方面差异性不大，且差异性随数据规模的增大而减小。

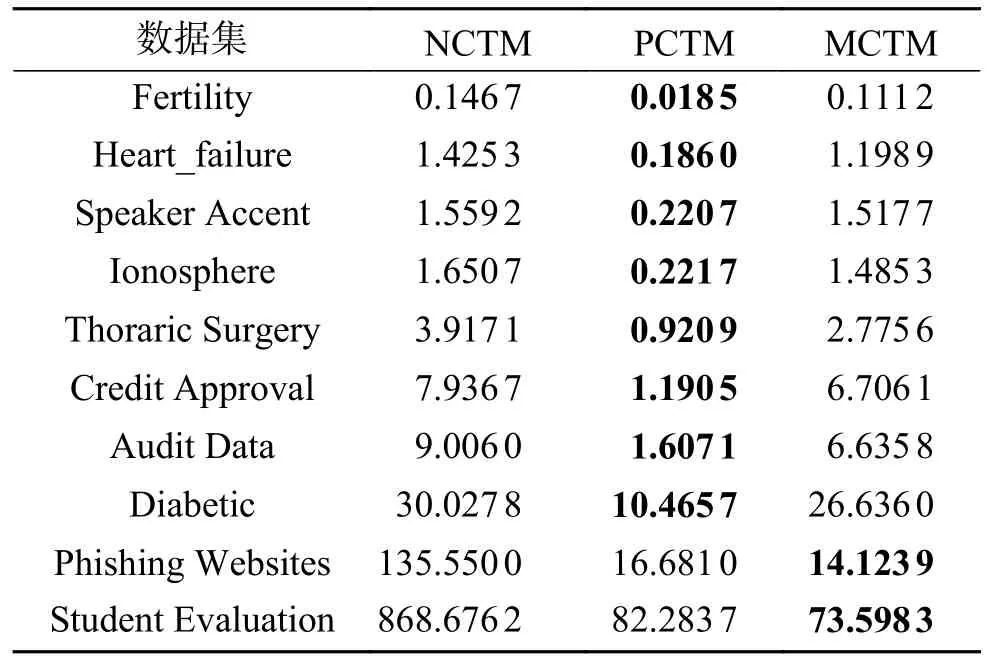
表7 3 种粗糙集模型的运行时间 Time(↓)对比Table7 Comparison of operation hours Time (↓)under three kinds of rough set models

综上所述，与其他2 种不同的粗糙集模型进行实验对比和分析可知，本文模型总体上具有较高的分类准确度和较低的误分类损失，因此，用其对混合邻域决策系统进行划分较为合理。

4.3.3 本文模型和序贯三支决策模型的边界域分类方法对比

为了进一步验证本文模型的有效性，本小节将本文模型与序贯三支决策的方法进行实验对比和分析。其中，MSTM (mixed-neighborhood rough set based sequential three-way decision boundary region processing model)是基于经典序贯三支决策[8]改造的基于混合邻域粗糙集的序贯三支决策边界域处理模型。实验结果如表8 所示，分别给出了MCTM 和MSTM 的分类准确度、权衡因子、误分类损失和时间的对比。

由表8 的实验结果可知，在数据集Ionosphere 和Audit Data 上，本文模型MCTM 的分类性能与MSTM 相同，而在另外8个数据集上，本文模型MCTM 的分类性能要优于序贯三支决策模型MSTM。从理论上分析，由于MSTM 直接由代价矩阵计算的阈值划分边界域对象，而本文在此基础上进一步考虑条件概率和误分类代价来划分边界域中的对象，因此本文模型MCTM 在Acc、F、Cost 和Time 上表现较优。为此，在同等条件下，对于混合邻域决策系统，本文基于属性约简的混合代价敏感三支决策边界域分类方法为处理边界域对象提供了一种可借鉴的分析方法。

5 结束语

近年来三支决策理论成为热点研究问题，其研究对象多为单一型决策系统，然而，在许多的应用领域中，数据往往呈现混合类型的特点，目前三支决策对混合数据边界域样本处理的研究相对较少。为划分混合决策系统中的边界域对象，本文提出了基于混合数据的属性约简方法；并在此基础上，提出了一种基于核属性的代价敏感三支决策边界域分类方法。通过在不同的数据集上进行实验对比与分析，验证了本文方法的可行性和有效性，获得了一种相对合理的边界域对象的划分方法。由于序贯三支决策更加符合现实生活中的决策过程及人类的认知，下一步工作将研究基于代价敏感的序贯三支决策的粒化问题。