轻钢龙骨-铝蜂窝夹层板复合墙板抗弯性能

吴凯凯,齐玉军

(南京工业大学 土木工程学院,江苏 南京 211800)

轻钢龙骨夹芯保温复合墙板是一种以轻钢龙骨为骨架、两侧安装覆面板、内部填充保温材料的轻质墙板,也称轻钢龙骨复合墙板。该复合墙板具有质轻、构件工厂化制作、干法施工以及环保节能等优点[1-2]。复合墙板作为建筑围护体系中的一员,不仅要具有承载能力,还要满足围护功能的要求。复合墙板的保温、隔热性能一般与龙骨截面特性、龙骨密度、龙骨间距、龙骨是否开孔、开孔参数、保温材料种类、覆面板种类等因素相关[3-7],而隔音性能主要由填充材料决定。覆面板一般通过自攻螺钉与龙骨连接,两者共同承担围护和承载的作用[8],覆面板承担的围护作用根据组成材料不同而表现出差异。覆面板组成材料通常选用水泥纤维板、石膏板、定向结构刨花板(OSB)、胶合板、钢板等,这类材料形成的覆面板均是实心板结构,且厚度较薄,此时覆面板对复合墙板的围护作用做出的贡献相对较小。

蜂窝夹层板是由两层薄而强的面板材料和中间厚而轻的蜂窝芯材复合而成。铝蜂窝是一种常见的蜂窝材料,由于铝材本身拥有密度小、延展性能好且难以被腐蚀等优点,因此常用于制作蜂窝夹层板。铝蜂窝夹层板具有比强度高、比刚度大、抗冲击性好、减振吸能好、可塑性强等优点[9];同时在隔热以及隔音方面也有巨大的优势,故常常被应用在航空航天、运输、家具、建筑等领域[10-11]。铝蜂窝夹层板具有较好的抗压能力和抗弯曲能力[12-14],是一种非常优异的墙体材料。

铝蜂窝夹层板在围护功能以及力学性能方面都具有明显的优势,因此本文提出一种采用铝蜂窝夹层板作为覆面板的新型轻钢龙骨复合墙板,对轻钢龙骨-铝蜂窝夹层板复合墙板的抗弯性能进行测试,研究复合墙板的厚度对其破坏模式和承载性能的影响,提出复合墙板屈服承载力的理论计算方法,为该新型复合墙板推广于实际工程提供依据。

1 试验方案

1.1 试件设计与制作

轻钢龙骨-铝蜂窝夹层板复合墙板由作为上下覆面板的铝蜂窝夹层板和作为中间骨架的轻钢龙骨组成,内部构成空腔结构,空腔内填充岩棉,如图1所示,铝蜂窝夹层板与轻钢骨架之间通过自攻螺钉连接,在接触面涂有高强度结构胶。铝蜂窝夹层板是由上下两层水泥纤维面板和铝蜂窝芯材通过结构胶黏结而成,其中水泥纤维面板厚度(hf)为8 mm,铝蜂窝芯材厚度(hc)为24 mm。

图1 复合墙板总体布置(mm)Fig.1 General layout of composite wall panels(mm)

本文设计了160和240 mm两种厚度(h)的复合墙板,记为LB-160和LB-240，复合墙板平面尺寸均为3 300 mm×600 mm。铝蜂窝夹层板厚度均为40 mm,通过改变纵向龙骨截面高度改变复合墙板的厚度。两块复合墙板纵向龙骨的截面形式均为U形,纵向龙骨翼缘宽(b)均为35 mm,厚度(t)均为0.8 mm。试件LB-160纵向龙骨腹板高度(hs)为80 mm,LB-240纵向龙骨腹板高度为160 mm,根据实际工程需要,LB-240的纵向龙骨由两根腹板高度为80 mm的U形龙骨并排焊接而成,焊点间距为250 mm。

复合墙板的覆面板由6块550 mm×600 mm的铝蜂窝夹层板拼接而成,如图1所示。复合墙板共设置两根纵向龙骨,龙骨间距为600 mm;在纵向龙骨之间设置了间距为550 mm的水平龙骨进行拉结,形成轻钢龙骨受力骨架,如图2所示。

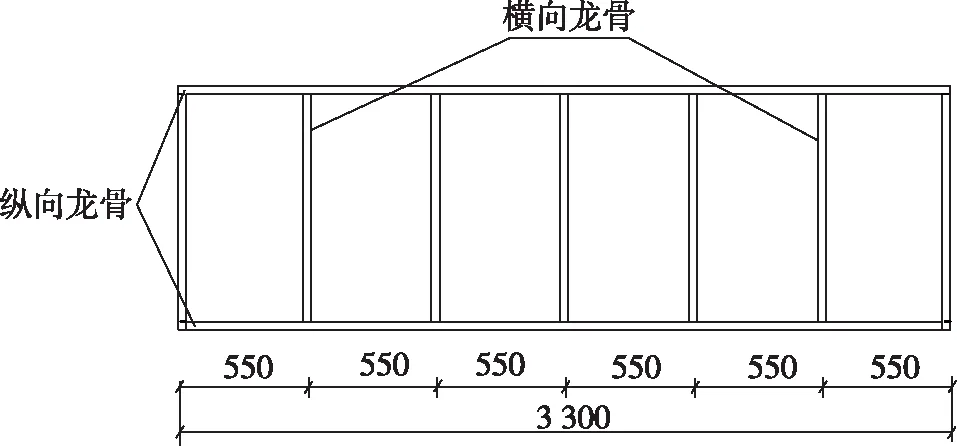
图2 龙骨布置图(mm)Fig.2 Layout of keel(mm)

本试验中钢材屈服强度(fy)为353 MPa,弹性模量(Es)为205 GPa,泊松比(v)为0.3;水泥纤维面板的弹性模量(Ef)为5 GPa。

1.2 测点布置

在跨中位置的上下两层覆面板表面沿复合墙板长度方向设置纵向应变片,在轻钢龙骨腹板沿高度方向布置纵向应变片,应变片1—15的位置如图3所示。为描述方便,将复合墙板的下覆面板外侧高度定义为0 mm(图3)。在复合墙板支座处、加载点处以及跨中位置处设置位移计,如图4所示。

图3 复合墙板截面构造以及测点位置示意(mm)Fig.3 Schematic diagram of composite wallboard cross-section structure and measuring point location(mm)

1.3 加载方式

复合墙板加载装置如图4所示。本次试验加载方式采用四点弯加载方式。在万能试验机上进行加载,采用位移加载,加载速度为0.5 mm/min,直至试件破坏或者当加载荷载降低到峰值荷载一半时认为试件失效,停止加载。

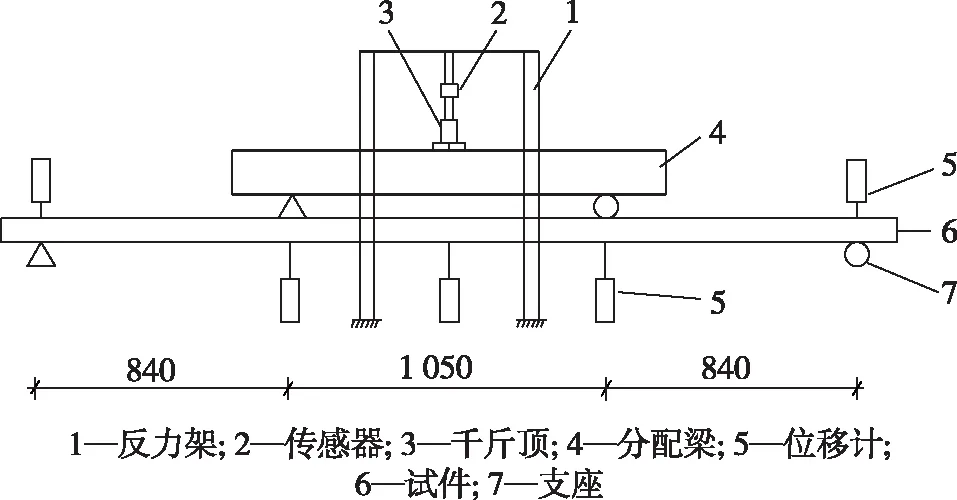
图4 复合墙板加载示意(mm)Fig.4 Schematic diagram of composite wallboard loading(mm)

2 试验现象和破坏模式

2.1 LB-160破坏过程

试件加载初期,试件整体工作性能良好,随着荷载的增加,复合墙板跨中截面的下覆面板处拼接缝间隙不断变大,下覆面板跨中处与自攻螺钉相连接处的水泥纤维面板角部出现裂纹,此时荷载为7.5 kN,如图5(a)所示。当加载到峰值荷载的90%时,右侧加载点处与下覆面板相连纵向龙骨腹板出现裂缝,此时自攻螺钉处的水泥纤维面板已被压溃,同时局部出现脱胶现象,如图5(b)所示。随着加载位移增加,裂缝不断发展,承载力开始下降,当荷载降至峰值荷载的95%时,裂缝长度扩展到纵向龙骨腹板宽度的一半,如图5(c)所示。当位移加载到120 mm时,试件沿着裂缝整体断裂,发生断裂破坏,如图5(d)所示。

图5 试件LB-160破坏过程Fig.5 Destruction process of specimen LB-160

2.2 LB-240破坏过程

在加载初期,试验现象与LB-160基本一致。随着荷载的增加,支座上方40 mm至120 mm高度范围内均出现了比较明显的鼓曲现象,如图6(a)所示,此时荷载为3 kN,试件整体刚度开始下降。随后支座处下覆面板的铝蜂窝芯材由于压缩导致变形越来越明显,如图6(b)所示。在支座上方120 mm至200 mm高度附近也出现明显的凹凸变形,支座处水泥纤维面板角部出现了裂纹。之后支座处下覆面板的铝蜂窝芯材被压扁直至压实,承载力开始下降,此时荷载为7.5 kN,如图6(c)所示。当支座处覆面板的铝蜂窝芯材被压实之后,承载力出现二次上升现象。随着荷载的增加,纵向龙骨腹板在左右支座附近、加载点附近及墙板跨中截面附近均出现凹凸变形即纵向龙骨腹板多处发生了局部屈曲破坏,如图6(d)所示。当承载力降低到峰值荷载的一半时,认为试件失效,停止加载。

图6 试件LB-240破坏过程Fig.6 Destruction process of specimen LB-240

3 试验结果对比分析

复合墙板的荷载-挠度曲线如图7所示。由图7可得：两种复合墙板试件均表现出典型的弹塑性受力特征,且均具有较好的延性变形能力。由图7还可得两种复合墙板存在不同之处：①弹性刚度不同,LB-240试件的弹性刚度大于LB-160试件的。这是由于在覆面板和轻钢龙骨翼缘相同的前提下,前者的截面高度大,所以截面的惯性矩也大,从而导致其抗弯刚度较大。②峰值荷载不同。LB-160的峰值承载力相对于LB-240提高了33%,这是由于LB-160中纵向龙骨达到了材料的破坏强度,最终发生了断裂破坏;LB-240由于腹板高度的提高导致腹板高厚比增大,此时纵向龙骨先发生了局部屈曲破坏,使其峰值承载力降低。③LB-240的荷载-挠度曲线出现突然变化的现象,主要是因为龙骨腹板屈曲导致了应力重分布、铝蜂窝夹层板出现了局部压缩。

图7 试件荷载-挠度曲线Fig.7 Specimen load-deflection curve

4 理论分析及计算

由于复合墙板的纵向龙骨壁较薄,板件的宽厚比较大,所以板件宽厚比在破坏过程中对构件的稳定承载力起到控制作用,故需要对板件的弹性屈曲临界应力进行计算。复合墙板上下覆面板为铝蜂窝夹层板,为了降低计算成本和提高计算效率,一般需要建立等效板模型[15-16]。

4.1 板件弹性屈曲临界应力计算

根据弹性稳定理论,板件弹性屈曲临界应力(σcrl)计算方法见式(1)。

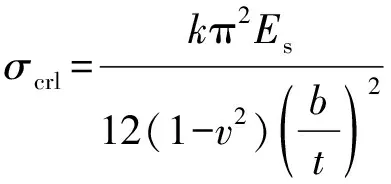
(1)

式中:k为板件的屈曲系数,根据文献[16]，对于纯弯的槽钢,腹板的屈曲系数(kw)为23.9,翼缘的屈曲系数(kf)为4。

由式(1)计算龙骨各板件的屈曲临界应力见表1。

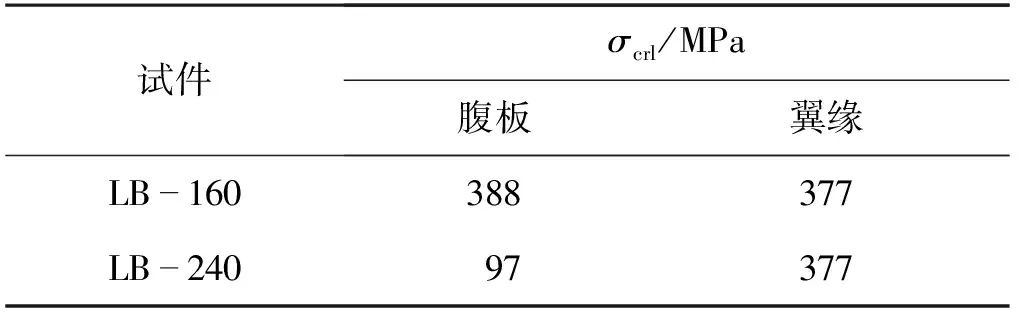
表1 龙骨各板件屈曲临界应力

由表1可得：LB-160的龙骨腹板以及翼缘的屈曲临界应力均大于钢材的屈服强度(353 MPa),说明复合墙板龙骨先发生屈服,并没有发生屈曲破坏;LB-240由于腹板屈曲临界应力(97 MPa)小于钢材屈服强度,复合墙板纵向龙骨腹板先发生局部屈曲,而且发生屈曲时间较早。

4.2 铝蜂窝夹层板等效板模型建立

由于铝蜂窝夹层板结构相对较为复杂,在计算时需要将其等效为等刚度的板。目前代表性的方法包括Allen理论[17]、Hoff理论[18]、Reissner理论[19-20]等。本文采用计算精度较高的Hoff理论进行计算,设定铝蜂窝夹层板满足以下假设:①假定面板同时具有面内刚度和弯矩刚度；②假定芯材不承受面内应力,不具有面内刚度；③忽略芯材和面板的法向应力分量,假定法向应力为0 MPa。

在Hoff理论中,铝蜂窝夹层板的等效参数计算方法见式(2)和(3)。

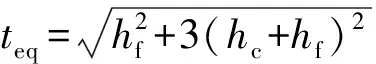
(2)

Eeq=2Efhf/teq

(3)

式中:teq为铝蜂窝夹层板的等效厚度,Eeq为铝蜂窝夹层板的等效弹性模量。

由式(2)和(3)计算铝蜂窝夹层板的等效参数:teq=56 mm,Eeq=1.43 GPa。

4.3 复合墙板屈服承载力计算

4.3.1 屈服点的确定

复合墙板由多种材料组合而成,其屈服点的确定受物理条件和应用条件两个因素影响[20]:①物理条件,即试件发生弹性破坏,进入塑性;②应用条件,即超出使用者的可接受范围。本文中复合墙板破坏模式分为两种：①纵向龙骨翼缘产生裂缝,之后裂缝迅速发展导致整体断裂;②纵向龙骨腹板发生屈曲破坏,之后支座处覆面板被压实,最后复合墙板纵向龙骨多处出现屈曲破坏,整体承载力下降。

本文采用最远点法进行屈服点的确定,即曲线上距离原点和峰值点所在直线的最远点为屈服点;若有多个最远点,屈服荷载取这些点对应荷载的平均值。

4.3.2 屈服承载力计算

试件破坏时,试件LB-160的纵向龙骨下翼缘已经屈服,计算时应力取屈服强度(fy);试件LB-240的龙骨腹板先发生局部屈曲,腹板变形迅速且幅度较大,故腹板屈曲临界应力取97 MPa(表1)。故对复合墙板屈服时截面应力进行假定:①不考虑下覆面板的抗拉作用;②复合墙板龙骨与覆面板不产生滑移;③满足平截面假定。

图8为跨中截面的应变分布,其中εa为等效上覆面板的应变;ε0为纵向龙骨上翼缘应变;εwc为受压区纵向龙骨腹板应变;εwt为受拉区纵向龙骨腹板应变;εy为纵向龙骨下翼缘应变;Ca为等效上覆面板内力;Csc为受压区纵向龙骨上翼缘内力;Cwc受压区纵向龙骨腹板内力;Twt为受拉区纵向龙骨腹板内力;Tb为受拉区纵向龙骨下翼缘应力;x为纵向龙骨下翼缘距中性轴距离;bc为等效板的宽度,本文取300 mm。

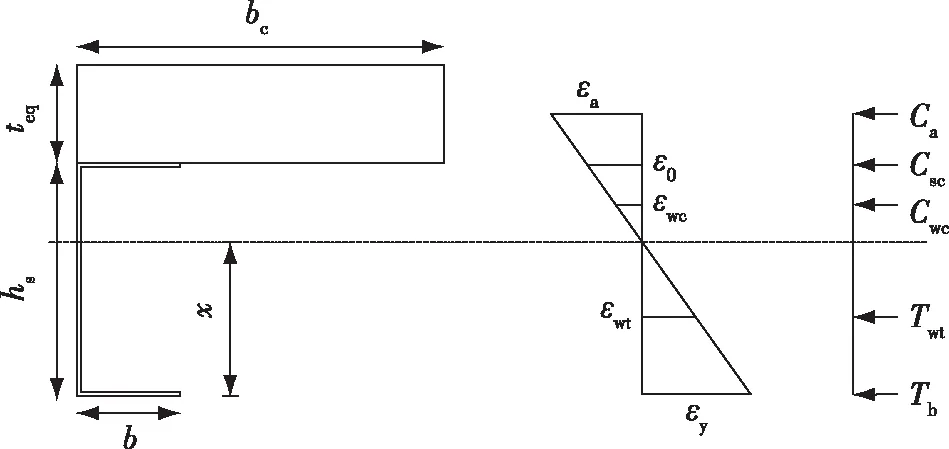
图8 跨中截面应变分布Fig.8 Strain distribution in the mid-span section

由内力平衡得式(4)。

Ca+Csc+Cwc=Twt+Tb

(4)

由式(4)可以求得LB-160和LB-240的x分别为73和122 mm。

复合墙板的屈服承载力计算方法为式(5)。

M=2[Ca(hs-x+teq/2)+Csc(hs-x-t/2)+

Cwc(hs-x-t)/2+Twt(x-t)/2+Tb(x-t/2)]

(5)

通过式(5)对两种复合墙板的屈服承载力进行理论计算,并与试验值进行比较,结果如表2所示。由表2可知:试件屈服承载力的试验值与理论值误差均在15%以内,说明复合墙板屈服承载力理论计算值与试验值吻合较好。

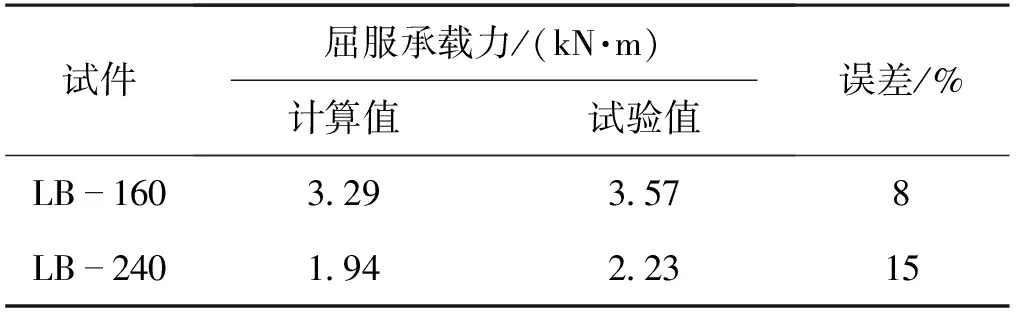
表2 屈服承载力试验值与理论值对比

5 结论

1)复合墙板的纵向龙骨截面高度较大且厚度较小时,会使纵向龙骨腹板的高宽比变大,导致腹板发生局部屈曲,此时复合墙板承载力反而会降低。

2)由于复合墙板的覆面板存在拼接缝,复合墙板在受弯时截面主要由纵向龙骨承受拉力,此时破坏位置容易发生在应力集中处即纵向龙骨与自攻螺钉连接处。

3)对于轻钢龙骨-铝蜂窝夹层板复合墙板可按照本文中方法对屈服承载力进行计算,且计算值与试验值吻合较好。