考虑初始空隙压密的岩石变形全过程本构模型

李修磊 ，陈洪凯 ，张金浩

（1. 重庆交通大学山区公路水运交通地质减灾重庆市高校重点实验室, 重庆 400074；2. 重庆交通大学土木工程学院, 重庆 400074）

岩石由于内部大量随机分布的微孔隙、微裂纹等初始缺陷，使得其力学性质和破坏机制变得非常复杂. 为了研究岩石的力学变形特性，国外学者对各类岩石（砂岩、花岗岩、大理岩、页岩等）开展了大量单轴和三轴试验研究[1-4]，结果表明，岩石的变形破坏特征对围压具有很强的依赖性，构建合理描述岩石变形破坏过程的本构模型是岩石力学研究的主要内容之一.

基于试验研究，许多学者对岩石的力学变形特性进行了大量的理论研究，也建立了相应的本构关系. Krajcinovic 等[5]首次将连续损伤和统计强度理论引入到岩石力学与破坏机制的研究中，随后国内外学者[6-10]也相继建立了一系列的岩石统计损伤模型，基于Lemaitre应变的等价理论[11]认为岩石损伤的本质是其内部形成缺陷（如空洞、裂隙等），而缺陷的承载能力几乎为0. 但该类模型有两个方面的不足：一是无法反映荷载应力较小时岩石的非线性弹性变形；二是难以准确描述岩石变形峰值强度后残余强度阶段的变形特征. 针对以上两方面不足，曹文贵等[12-13]基于微元强度的概念，认为微元强度服从Weibull随机分布，且微元损伤后以残余强度的形式承担荷载，考虑岩石破坏后的残余强度变形特征，提出了能够模拟岩石峰值后破坏变形特征的损伤统计模型；刘冬桥等[14]依据三轴试验结果提出了岩石损伤变量的演化方程，基于微元强度概念发展了相应的损伤本构模型，用于描述岩石的应变软化；Li等[15]考虑了围压对岩石脆性指标的影响，认为微元强度服从Weibull分布、正态分布和幂函数分布，分别建立了对应的岩石损伤本构关系. 上述几种模型均认为岩石在屈服前呈线性弹性变形，与实际情况差别较大. 另外，曹文贵等[16]通过考虑荷载作用下岩石内部空隙体积的变化和损伤阈值，建立了岩石的统计损伤模型，一定程度上反映了低应力水平下岩石的非线性变形特征，但不能很好反映岩石破坏过程的变形规律. Xu等[17]虽考虑了岩石内部空隙的压密，并基于断裂损伤理论建立了相应的本构模型，但峰值后的破坏变形与试验结果差别较大.

基于上述分析，大部分岩石本构模型能够合理描述岩石部分阶段的变形特征，很少有模型能够准确模拟岩石的变形全过程，关键在于现有模型对岩石的力学变形机理难以准确反映，本文将根据荷载作用下岩石的变形全过程特征，分析岩石的力学变形机理，基于统计损伤理论，以期建立岩石的损伤统计本构模型用于合理模拟岩石变形破坏的全过程.

1 岩石变形力学机理与分析

1.1 岩石变形过程的力学机理

外部荷载作用下岩石的变形可划分为两部分：一是由岩石骨架产生；二是由岩石内部空隙产生. 较小荷载应力下岩石骨架和空隙部分将同时产生变形；当荷载应力增加到一定程度时，岩石内部空隙闭合完成，此时岩石仅发生线弹性的骨架变形；荷载应力进一步增加超过岩石屈服强度后，岩石发生非线性的骨架变形，出现屈服、应变软化和完全破坏的变形阶段. 岩石破坏变形全过程示意如图1所示. 图中：Δ ε1为骨架部分应变与总应变之差；Δ εa为初始时刻骨架部分应变与总应变的差值（即为岩石总的空隙应变）；εa和 σa为空隙完全闭合时的轴向应变和应力；σc和 εc分 别 为 峰 值 应力和峰值应变；σ1−σ3为偏应力，σ1为大主应力，σ3为小主应力（围压）； ε1为轴向应变. 由图1可知：OA为初始空隙压密段、AB为线弹性变形段、BC为屈服段、CD为应变软化段和D点后为完全破坏阶段.

图1 岩石破坏变形全过程示意Fig. 1 Whole failure and deformation process of rocks

1.2 岩石内部空隙部分变形的分析方法

为了分析荷载应力下由岩石内部空隙部分产生的变形，在岩石内部取一个有代表性的柱体单元，如图2所示，空白处表示空隙部分，阴影处表示骨架部分. 设加载前柱体单元初始总高度为h0，岩石骨架部分的高度为h0s，空隙部分的高度为h0g；若某荷载应力 σ下岩石柱体单元总变形量为 Δh，岩石骨架和内部空隙分别产生的变形量为 Δhs和 Δhg，则

图2 岩石变形分析模型Fig. 2 The deformation analysis model of rocks

荷载应力 σ作用下岩石的总应变 ε、骨架部分应变 εs以及空隙部分应变 εg可分别表示为

由式（4）可知：若要分析荷载应力 σ作用下的 εg，须先获得空隙部分的变形量 Δhg. 为此，将 σ划分为由n个等级组成的应力增量 Δ σt逐级施加，即

将应力增量 Δ σt作用下岩石骨架部分和空隙部分 的 变形量分别记作 Δhts和 Δhtg，相应的应变增量分 别记 作 为 Δ εts和 Δ εtg，岩石 的 总应 变 增量 Δεt=Δεts+Δεtg，骨架部分和空隙部分的总变形量 Δhs和Δhg可 分别视为 Δhts和 Δhtg的 累加. 岩石总 应变、骨架以及空隙部分的应变可表示为

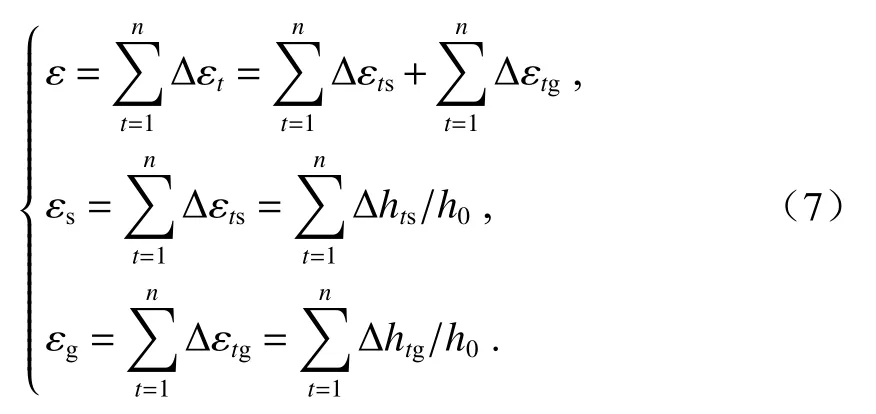
令应力增量 Δ σt作用下空隙部分的应变增量Δεtg所占岩石总应变增量 Δ εt的比例为kt（即 Δεtg=ktΔεt），则 Δ εts=(1−kt)Δεt. 若应力增量 Δ σt和骨架部分的应变增量 Δ εts服从广义Hook定律，则

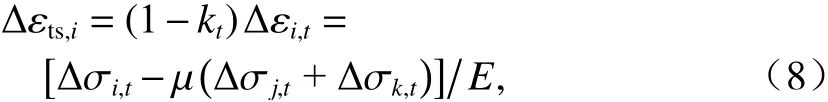
式中：Δ εts,i为骨架部分在i方向上的应变增量；E和µ分别为岩石骨架的弹性模量和泊松比，其中，E即为岩石应力-应变线弹性阶段的变形模量；i=1，2，3，j=2，3，1，k=3, 1, 2，分别表示三维空间上的主应力和主应变的方向；Δ εi,t为应力增量 Δ σt作用下i方向上的总应变增量，余同；Δ σi,t为主应力i方向的应力增量，余同.

利用式（6）和式（7），对式（8）等号两侧进行求和可得

式中：εi为i方向上的总应变；K为空隙应变比，如式（10）；Δ εi,tg为应力增量作用下i方向上的空隙应变增量，εi,g为i方向上的空隙应变.

1.3 空隙应变比K的确定

由岩石的轴向应力-应变试验曲线（如图3）可知：初始空隙压密阶段的轴向应力-应变曲线表现出明显的非线性，此阶段轴向刚度随着应力的增加在逐渐增大；线弹性阶段的轴向刚度随应力的增加近似为定值；若不考虑应力-应变曲线的微小波动，则空隙完全闭合的应力点对应于由非线性增长向线性增长过渡的转折点.

将图3中线弹性阶段（AB）的试验数据进行回归分析，即可得到图3中蓝色直线的线性方程为

图3 应力-应变试验曲线Fig. 3 Stress-strain test curve

式中：b为斜率，其值等于岩石的弹性模量E，MPa；c为纵轴（偏应力轴）上的截距，MPa；b和c均为正值.

岩石的轴向总空隙应变 Δ εa等于图3中蓝色直线在横轴（应变轴）上的截距，可表示为

偏应力水平相同时，利用式（11）求解得到的轴向应变减去对应的试验轴向应变，可得到应力相同时图3中蓝色直线与试验曲线之间的 Δ ε1，如式（13）.

利用式（13）求解并绘制 Δ ε1与偏应力之间的关系曲线，如图4所示. 由图4可确定随着偏应力增大轴向应变差初始等于0的A点，该点对应着空隙闭合完成时的轴向应变 εa，A点之前则对应着初始空隙压密阶段，B点对应着屈服应力点.

图4 轴向应变差-偏应力曲线Fig. 4 Axial strain difference -deviatoric sress curve

岩石骨架部分的应变可用式（11）在c值为0时进行求得，也就相当于图3中的蓝色直线向左平移c/b个单位长度，使其通过坐标原点. 岩石空隙部分的轴向空隙应变ε1g如式（14）. 当 ε1≥εa时，岩石内部空隙完全闭合，空隙应变不再发生变化.

利用多功能试验机对砂岩试样（φ 50 × 100 mm）开展三轴压缩试验，得到了不同围压下的轴向应力-应变关系曲线，如图5所示. 由应力-应变试验曲线，利用式（11） ～ （14）可以得到 ε1g与 ε1之间的变化关系，如图6所示. 由图6可以看出：砂岩的空隙应变随着轴向应变的增加而增大，且增加幅度逐渐减小，应变水平较大时逐渐趋近于定值；应变水平较小时，不同围压下砂岩试样的空隙应变非常接近；随着轴向应变的增加，不同围压下砂岩空隙应变的差异性逐渐显现，应变水平较大时近似为定值的空隙应变随着围压的增加呈现出先增大后减小的变化趋势.

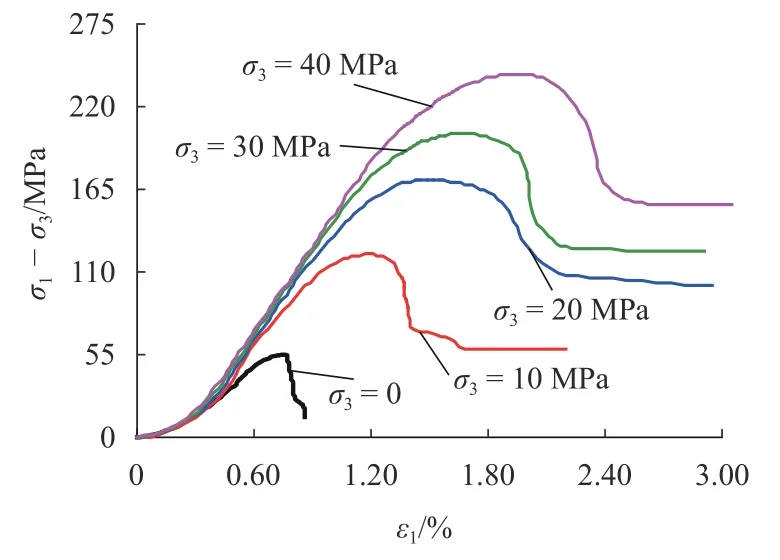
图5 砂岩的三轴试验结果Fig. 5 Triaxial test results of sandstone

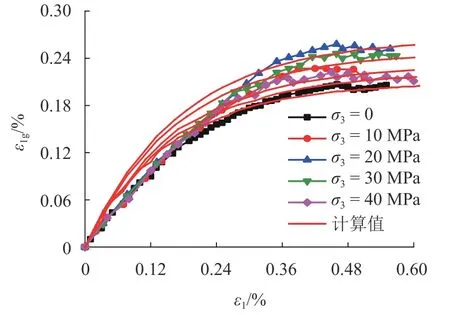
图6 轴向空隙应变随轴向应变的变化规律Fig. 6 Variation of void strain with axial strain

利用式（14）对图6中的试验曲线进行拟合，可得到空隙应变比K随 ε1变化的表达式为

式中：a1和a2均为计算参数，其中，a1为图3中直线方程式（11）与轴向应变轴的交点，即为c/b，a1可通过对岩石应力-应变曲线的线弹性段回归分析获得，a2可利用式（14）对确定的 ε1g- ε1关系曲线（见图6）拟合获得.

2 岩石损伤本构模型的建立

2.1 损伤模型的构建

基于Lemaitre [11]提出的应变等价性，将岩石承受的宏观名义应力和净应力与其有效承载面积的减小建立联系. 假定岩石由众多微元均匀组成，所有微元在荷载作用下划分为损伤和未损伤两部分，且荷载由这两部分共同承担. 图7给出了岩石损伤的转化过程. 图中：空白部分的面积为S1表示未损伤部分，阴影部分的面积为S2表示损伤部分；σi为岩石整体受到的宏观名义应力：σ∗i为未损伤部分受到的净应力；Rs为损伤部分受到的净应力. 初始时刻总面积S=S1，S2=0；岩石完全破坏时S=S2，S1= 0；损伤变量D如式（16）所示.

图7 损伤转换过程示意Fig. 7 Sketch of the damage transition process

取岩石微元进行分析，由静力平衡条件可得外部荷载为

联立式（16）和式（17），可得

考虑岩石内部空隙压密的变形特征，根据广义Hook定律，由式（9）和式（10）可得

将式（18）代入式（19）中，考虑常规三轴试验条件下有 σ2=σ3，通过整理可得到反映岩石全应力-应变特征的本构方程，如式（20）.

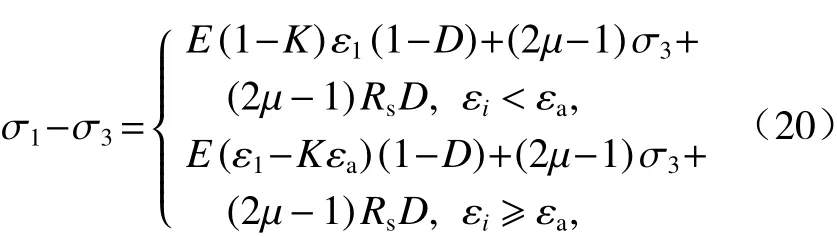
2.2 损伤部分残余强度的计算

随着外荷载的增加，岩石内部有效微元数目逐渐减少，未损伤区域S1逐渐转化为损伤区域S2，直到完全损伤. Menendez等[18-19]认为岩石中微裂纹贯通形成剪切带后，其强度主要依赖于剪切带上的摩擦作用，黏聚力几乎完全消失. 因而，可采用残余强度Re来替代Rs，利用Mohr-Coulomb强度准则计算：

式中：cr和 φr分别为岩石残余强度对应的黏聚力和残余内摩擦角.

由岩石三轴试验结果可得不同围压下岩石的残余强度Re，进而得到残余强度参数.

2.3 损伤变量的演化

岩石内部的缺陷会削弱其承载能力，这些缺陷在岩石内部可以看作是随机分布. 因此，从统计损伤的角度出发，认为岩石损伤是一个连续的应力过程，采用微元强度分布对岩石进行定量分析. 现有研究大多认为岩石微元强度服从Weibull函数分布[7-10,12,17,20]，本文采用相同的微元强度分布规律，相应的概率密度函数为

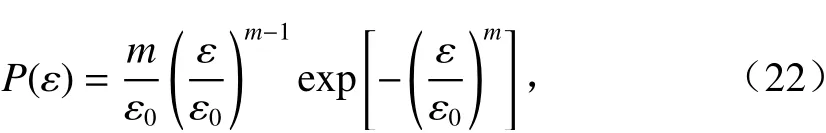
式中：m和 ε0分别为形状参数和尺寸参数.

外部荷载作用下，应变达到一定值时岩石内部损伤区域为

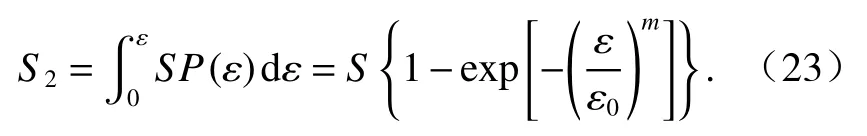
由式（16）和式（23）可得岩石损伤变量的演化方程为

将式（15）和式（24）代入式（20）中，即可得到基于Weibull分布的岩石统计损伤本构关系如下：

1） 当 ε1<εa时

2） 当 ε1≥εa时

为了得到上述Weibull分布的参数m和 ε0，对式（25）进行整理后求对数，得到如下形式：

1） 当 ε1<εa时

2） 当 ε1≥εa时

式（26）右侧可以看作是因变量，左侧第一项lnε1可看作是自变量，m可视为斜率，−mlnε0为截距. 通过对现有不同围压下岩石的实测试验数据，利用式（26）进行线性回归，可得到Weibull分布的参数m和 ε0.

图8给出了不同m值对应的损伤变量D随ε/ε0的变化关系. 由图可看出：D随 ε/ε0的增加而增大； ε/ε0<1 时，m值越大意味着同等应力水平下岩石的损伤程度越小，且 ε/ε0>1 时，m值越大意味着同等应力水平下岩石的损伤程度越大，岩石越快达到完全损伤状态（D= 1）.

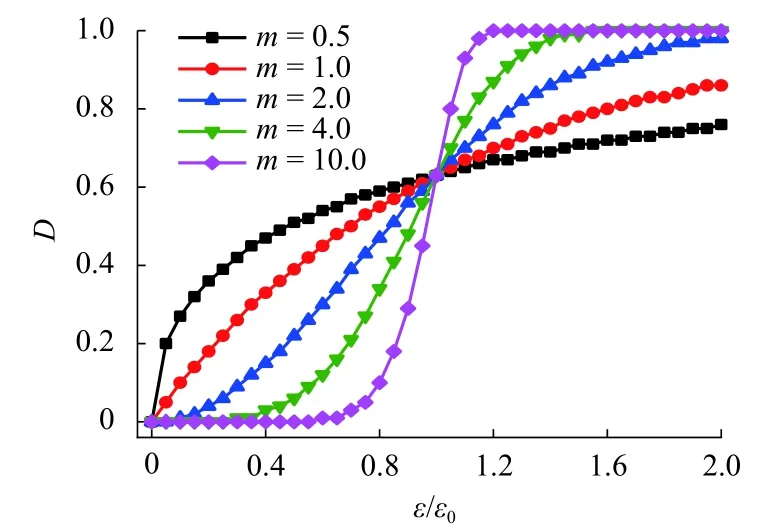
图8 不同m值对应的损伤变量D随ε/ε0的变化Fig. 8 Variation of damage variablesD with ε/ε0 for differentm

3 试验验证与讨论

3.1 试验结果分析

利用多功能电液伺服试验机对砂岩试样开展单、三轴压缩试验测，试样直径为50 mm，高度为100 mm. 试验过程中采用位移控制，加载速率为0.002 mm/s，围压分别取0、10、20、30、40 MPa. 由试验所得不同围压下砂岩的轴向应力-应变关系曲线（图5）可以看出：不同围压下砂岩的应力-应变曲线具有明显的阶段性特征. 表1给出不同围压（σ3）下砂岩的弹性模量E、空隙完全闭合时的 εa、σc、εc和R. 可以看出：砂岩的E、σc、 εc和R随着围压的增加均呈增大趋势，而 εa随围压的增加而减小. 由Morh-Coulomb强度准则，可得到该砂岩峰值强度对应的黏聚力（cc）和内摩擦角（φc）分别为12.08 MPa和44.6°；残余强度对应的黏聚力（cr）和内摩擦角（φr）分别为0.12 MPa和37.4°，岩石的泊松比+ µ = 0.21.

根据前述确定模型参数的方法，基于试验结果得到了与空隙应变比K相关的参数a1和a2，以及与损伤变量D相关的参数和m，见表2.

根据表2中对试验数据进行反演得到的模型参数，从而得到相关模型参数与围压 σ3

之间的函数变化关系，如式（27）. 可知：随着围压 σ3的增大，a1先增加后减小，a2近似线性减小，ε0近似为线性增加，m大致呈指数形式的减小.

由表1和表2可知：该模型中Weibull分布参数 ε0略 大 于 εc，不 同 围 压 下 ε0−εc的 平 均 值 为0.103. 图9给出了 ε0与 εc之间的关系曲线. 可以看出：两者之间具有很好地一致性. 因而为了方便计算可用应力-应变曲线对应的峰值应变 εc+ 0.1来代替Weibull分布参数 ε0.

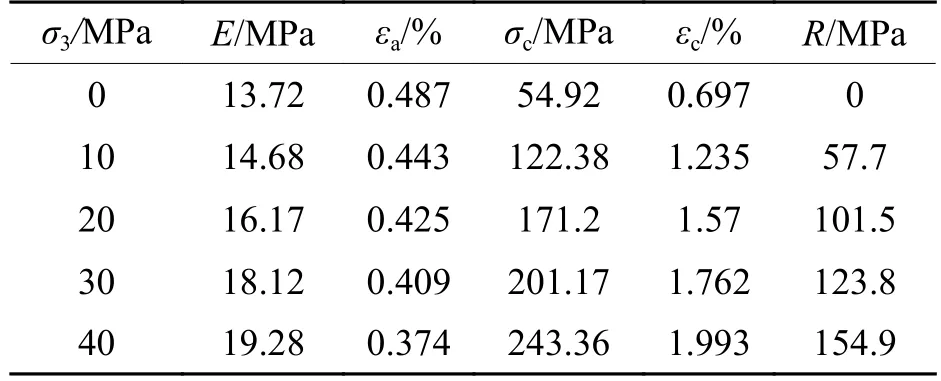
表1 岩石三轴试验参数Tab. 1 Triaxial test parameters for rock

表2 本文岩石统计损伤模型参数Tab. 2 Parameters of statistical damage model for rocks

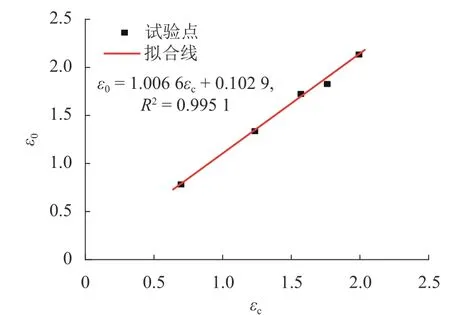
图9 Weibull分布参数ε0与εc的关系Fig. 9 Relationship between peak strainεc and the parameterε0 of Weibull distribution

3.2 模型验证

以下采用砂岩试验数据对本文所建岩石的损伤统计本构模型进行验证，本文模型计算结果与试验数据对比情况如图10所示. 可以看出：本文模型在不同围压条件下的计算结果与试验曲线均有较高的吻合程度，很好地反映荷载作用下岩石破坏变形的全过程，尤其是初始空隙压密及屈服后各阶段的非线性变形特征，从而验证了本文所建岩石本构模型的合理性.

图10 本文模型计算结果与试验曲线之间的比较Fig. 10 Comparison between the proposed constitutive model calculation values and experimental curves

以围压 σ3=30 MPa条件下砂岩的试验数据为例，模型参数的取值见表2，比较已有模型和本文模型对试验数据的模拟效果，如图11所示. 可以看出：由于文献[12]和文献[20]建立的岩石损伤本构模型均未考虑初始空隙压密对岩石变形的影响，导致模型计算结果在初始段呈线性弹性变化，与试验曲线差别较大；由于文献[12]模型没有考虑岩石破坏后的残余强度，导致其残余强度变形阶段与试验曲线有很大差别. 可见，本文所建模型能够较好地模拟岩石应力-应变全过程5个阶段的变形特征.

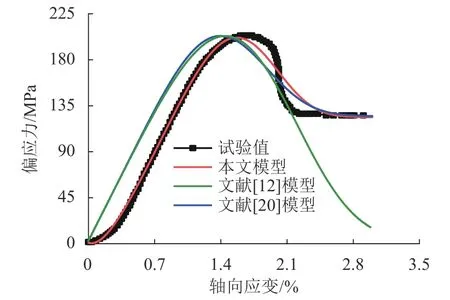
图11 不同模型计算结果与试验值的比较Fig. 11 Different model calculations versus experimental curve

4 结 论

1） 将岩石抽象为由实体骨架和内部空隙两部分组成的材料，分析了这两部分的变形机理以及与岩石整体变形之间的关系，提出了空隙应变比K的概念，建立了岩石的变形分析模型，奠定了荷载作用下岩石破坏变形全过程模拟方法研究的基础.

2） 利用三轴试验结果，推导了空隙应变比K的演化方程，结合岩石变形的分析方法，基于损伤统计理论并考虑岩石破坏后的残余强度变形，建立了能够合理描述岩石变形破坏全过程的损伤统计本构模型，初始空隙压密阶段及随后各阶段的变形特征均能得到较好的反映，不同围压下所建模型与试验结果均有较高的吻合度，相比现有模型更为合理.

3） 通过本文模型、现有相关模型和试验曲线的比较，验证了本文所建岩石损伤模型的有效性和合理性.

致谢：中国博士后科学基金（2018M633627XB）.