钢轨轧制不平顺激扰下的动车组动力响应特性

杨 飞 ，吴细水 ，孙宪夫 ，魏子龙 ，柯在田 ，杨爱红

（1. 中国铁道科学研究院集团有限公司基础设施检测研究所, 北京 100081；2. 中国国家铁路集团有限公司工电部,北京 100844）

我国200～250 km/h速度级的客运专线多采用有砟轨道结构形式. 在有砟轨道运营初期，由于散粒体道床结构相对松散，其平顺状态易受到线路设备初始状态、列车荷载、地质条件和养修作业等因素的影响. 其中，钢轨作为重要的轨道结构部件，其服役状态对轮轨相互作用、车辆运行的安全性和平稳性都有重要影响，也是造成有砟轨道几何形位快速发展劣化的重要因素之一. 最为常见的钢轨伤损形式是焊接接头伤损和钢轨擦伤，此外还有钢轨硌伤、母材伤损、波磨、小曲线半径钢轨侧磨、锈蚀等[1-2]. 在上述钢轨病害中，易诱发和加剧轨道不平顺的钢轨问题可以归为两类：一是与焊接工艺和焊接材料等因素有关的焊接接头低塌不平顺，在列车荷载反复作用下恶化较为迅速；二是钢轨轨身在轧制过程中产生周期性高低不平顺，此类不平顺自铺轨后就一直存在于线路上，对车辆和轨道结构的维护和使用寿命均带来不利影响.

针对上述钢轨状态不良引起的轨道不平顺，国内外学者从检测、评价、整治措施以及对行车品质的影响等方面入手，开展了大量研究工作. 针对焊接不平顺问题，高建敏等[3]采用动力学模型仿真分析了焊接区低塌不平顺波长和幅值对轮轨动力响应的影响，并提出安全限值. Deng等[4]连续5 a对焊缝进行监测，并提出低塌形成和发展过程的假设，通过轮轨相互作用三维有限元模型数值分析得到证实. 刘永乾等[5]针对有砟客专在钢轨轨端2.2～2.8 m处的低塌不平顺，提出多种作业方式相结合的打磨整治方案，并用动力学仿真分析打磨效果. 魏子龙等[6]建立了考虑有砟道床非线性支撑的轮轨瞬态接触有限元模型，研究钢轨焊接接头处轨枕空吊间隙和数量对轮轨作用的影响. 围绕钢轨轧制不平顺问题，研究表明用于矫直钢轨的滚轴周长约3.0 m，这会使钢轨产生波长为3.0 m的原始不平顺[7]. Srimani等[8]基于有限元模型提出了在特定矫直机加载参数条件下估计钢轨平直度的方法，对钢轨两端切割长度具有指导意义. Wang等[9]采用有限元分析复合矫直所引起钢轨几何尺寸的变化特征，同样提到在锯切轧制件时，应考虑矫直工艺对截面尺寸和长度的影响. 刘秀波[10]以秦沈线为例，采用小波分析与经验模态分解识别波长为3.0 m的钢轨波浪弯曲不平顺. 马晓川等[11]发现某18号道岔上钢轨轧制不平顺的主波长是0.8 m的整数倍，借助车辆-道岔耦合动力学模型分析了其对轮轨垂向相互作用的影响. 陈宪麦等[12]在分析高铁轨道不平顺谱中发现，轨身存在钢轨轧制引起的波长为2.84 m的周期性不平顺. 上述研究多采用轨道几何检测数据分析和数值模拟等方法，鲜有涉及有砟客专线路轧制不平顺的研究，特别是车辆各部件振动响应与轮轨接触力在钢轨轧制不平顺激扰下演变的试验研究，钢轨轧制不平顺已成为影响高铁线路运行品质的新问题和挑战.

根据路局反映，某新建有砟客专运营列车在部分区段存在“抖车”现象，轨道几何动态检测的高低不平顺波形显示该区段存在谐波特征. 针对这一问题，本文首先分析了异常区段动检数据的时频分布特征，并结合大机捣固作业效果和钢轨矫直原理来诊断引起这一异常现象的成因. 通过分析实测车辆各部件的振动加速度和轮轨力，得到钢轨轧制不平顺对车辆各部件动力响应的影响规律，以期为制定相关管理标准和指导现场养护维修提供理论参考.

1 动态检测数据的异常特征

1.1 波长特征

某新建有砟客运专线动检数据显示，部分区段存在高低不平顺和车体垂向加速度谐振波形，如图1所示. 可以看出：两个行别均存在由32.6 m简支梁引起的周期性高低不平顺，其特征波长为32.7 m（含梁缝）. 上行的高低不平顺和车体垂向加速度还存在波长为3.2 m的周期性波动特征，导致高低不平顺峰峰值接近2.0 mm，车体垂向加速度峰峰值接近1.00 m/s2，添乘人体感受车辆竖向抖动，而该处下行并不存在这一特征.

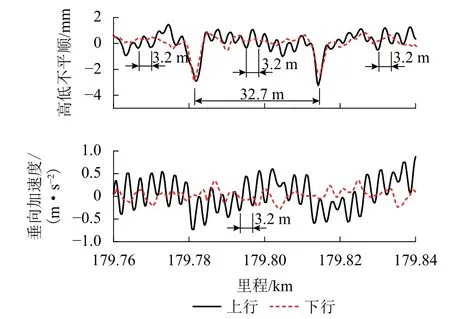
图1 动态检测数据波形Fig. 1 Waveforms of dynamic detection data

两个行别的K178+500～K181+000区段检测数据功率谱密度（power spectral density, PSD）如图2所示. 从图2（a）可以看出：两个行别主波长均为32.7 m，其倍频处存在8个明显的谱峰，波长分布在3.6～16.4 m，这均与简支梁变形周期性高低不平顺相关. 两个行别明显区别在于仅上行存在波长为3.2 m的谱峰，其2倍频1.6 m处也存在明显谱峰.从图2（b）可以看出：上行车体垂向加速度同样在3.2 m处的成分更为显著.

图2 动态检测数据PSDFig. 2 PSD of dynamic detection data

1.2 时频分布特征

传统的时频分析方法存在低频（长波）的空间分辨率不足、高频（短波）的频率分辨率和能量聚集性差等问题，同步压缩变换是在已知的时频分布基础上，利用信号瞬时频率附近的相位信息对时频分布进行频率重构. 同步压缩小波变换（synchrosqueezed wavelet transform，SWT）将同步压缩技术与连续小波变换相结合，显著提高了时频分辨率和能量聚集度，从而增强时频分布的可读性[13].

时域信号s(t)的连续小波变换系数谱为

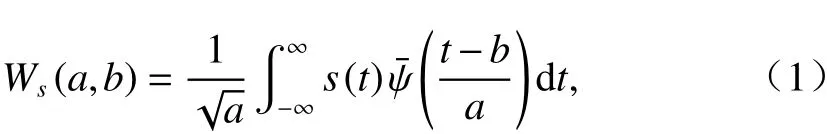
式中：a为尺度因子；b为时间平移因子；(•)为母小波函数的共轭复数；t为时间（或空间里程）.

虽然小波变换系数谱在尺度方向上发生能量扩散，导致时频谱模糊化，但其相位信息不受尺度的影响. 当 任 意 一点Ws(a,b)≠0 时，信 号s(t)的瞬 时 频率为

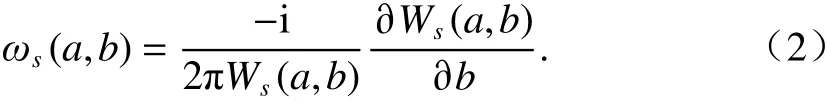
由式（2）建立从时间-尺度（b,a）到时间-频率平面（b,ωs(a,b)）的 映射，完成同步压缩. 将ωs(a,b)简化为ω(a,b)，对于离散情况，尺度参数和频率参数均为离散值，小波变换的时间-尺度分布可以重新分配为

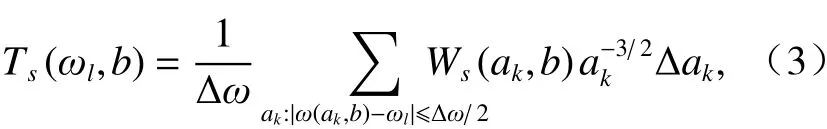
式中：Ts(ωl,b) 为同步压缩小波变换量值；ωl为第l个离散角频率；ak为第k个离散尺度，k=1,2,···,n；Δak=ak−ak−1为尺度坐标步长；Δω=ωl−ωl−1为频率坐标步长.

由式（3）可知：同步压缩使连续小波变换后的时频谱能量聚集至瞬时频率方向，提高了时频分辨率.

上行方向动态检测数据的SWT时频分布如图3所示. 由图可知：高低不平顺和车体垂向加速度均在波长3.2 m处存在明显“亮带”. 左高低不平顺存在2段“亮带”，分别命名异常区段 ①、②；右高低不平顺存在3段“亮带”，分别命名异常区段 ③～⑤. 左、右高低不平顺异常区段沿线路分布里程并不一致. 车体垂向加速度存在2段“亮带”，涵盖全部高低不平顺异常区段，这说明车体垂向异常振动是由高低不平顺所致.

图3 上行动态检测数据SWT时频分布Fig. 3 SWT time-frequency distribution of uplink dynamic detection data

2 周期性高低不平顺成因分析

2.1 大机捣固对周期性不平顺的影响

存在异常的上行K178 + 500～K181 + 000区段捣固作业前、后的动态高低不平顺和车体垂向加速度PSD如图4所示. 可以看出：高低不平顺和车体垂向加速度在波长32.7 m及其倍频3.6～16.4 m处的谱峰幅值均显著降低，大机捣固改善了由于简支梁引起的周期性高低不平顺；但1.6 m和3.2 m处的谱峰依然存在，说明大机捣固未能改善这种异常的周期性高低不平顺.

图4 捣固作业前、后动态检测数据PSDFig. 4 PSD of dynamic detection data before and after tamping operation

动、静态高低不平顺的主要区别是有无列车荷载，二者的差异一定程度上能够反映轨下结构的弹性状态. 有砟轨道动、静态高低不平顺差异较大的处所可能存在翻浆冒泥、暗坑或轨枕空吊等病害. 但两者的检测原理存在明显区别，动态高低不平顺描述的是轨面相对于车体动态基线的相对偏差，静态高低不平顺描述的是10 m中点弦测值. 因此，采用式（4）将动态高低不平顺按10 m中点弦测输出[14].

式中：qi、fi分别为第i个点动态高低不平顺的10 m弦测值和幅值；fi−r和fi+r分别为第i个点所在10 m弦起点和终点处的动态高低不平顺幅值，r为中点矢距的采样间隔.

当输入的动态高低不平顺为正弦波时，对式（4）作傅里叶变换并整理，得到10 m中点弦测法的传递函数为

由式（5）可知：10 m中点弦测法的传递函数在0～2波动，弦测值相比于真实值存在将其夸大或缩小特征. 捣固后的动态高低不平顺按式（4）输出，将其与静态高低不平顺检测结果绘于图5中. 可以看出：动、静态高低不平顺均存在波长为3.2 m的周期性波动特征，动态的振幅比静态更大. 动、静态高低不平顺峰值差的最大值位于焊缝位置，达到2.2 mm，其余位置峰值差均未超过1.0 mm. 说明除焊缝位置外，轨道弹性状态较好，异常周期性高低不平顺不是由轨下结构弹性状态不良引起. 图6绘制了捣固后动、静态高低不平顺功率谱，两者均在波长3.2 m处存在明显谱峰. 结合10 m中点弦测法传递函数，该波长的增益达到1.93，弦测值相比于真实值会被放大. 动、静态高低不平顺功率谱在波长3.2 m处的谱峰幅值相差不多，进一步佐证了轨下结构弹性状态不是引起异常周期性高低不平顺的诱因.

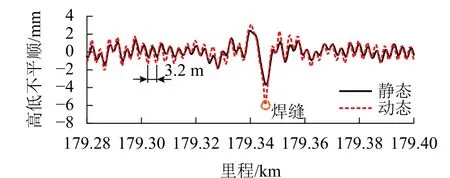
图5 捣后动、静态高低不平顺Fig. 5 Dynamic and static longitudinal unevenness after tamping

图6 捣后动、静态高低不平顺PSDFig. 6 PSD of dynamic and static longitudinal unevenness after tamping

2.2 不平顺区段的空间分布

为了分析某一波长成分所携带的能量随时间（或空间里程）的变化规律，将指定频带内的SWT的均方根（root mean square，RMS）定义为指定频带内小波能量集（summed wavelet power in different frequency band, SWP），如式（6）所示.

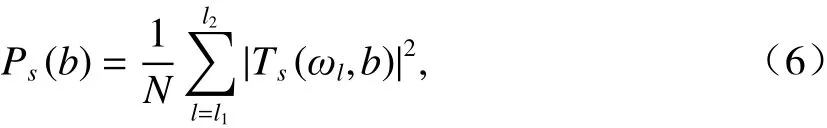
式中：Ps为信号s(t)的SWP；N为指定频带（波段）内的采样点数；l1、l2分别为最小、最大截止波长对应的点号.

图7绘制了3.0～3.5 m波段的小波能量集，可以看出：5个异常区段的SWP明显大于正常区段.根据SWP突变位置可识别出异常区段大致的起、终点里程，以异常区段 ① 为例，识别出起点位于K178+ 850附近，该处左高低不平顺如图8所示. 图示区段共有5孔32.7 m简支梁，捣固后梁缝处高低不平顺明显改善. 钢轨焊缝位于第3孔梁上，距小里程方向的梁缝9.0 m. 线路在捣固后经过一段时间运营，此处焊缝的高低不平顺进一步发展，从−2.1 mm增至−3.4 mm. 将高低不平顺经2.0～4.0 m带通滤波后发现，波长为3.2 m的异常特征均位于焊缝朝大里程方向一侧，由此确定异常区段 ① 的起点位于K178 + 850的焊缝处，并且捣固前、后异常区段带通滤波的高低不平顺幅值基本无变化. 同理复核出这5个异常区段起终点均位于焊缝位置，高低不平顺的3.2 m周期性特征在2个焊缝间持续存在. 各异常区段精确起、终点里程见表1，可以看出：异常区段的持续长度和相邻异常区段的间隔均是百米定尺钢轨长度的整数倍. 结合上述特征可以得出：异常周期性高低不平顺与钢轨状态引起密切相关.

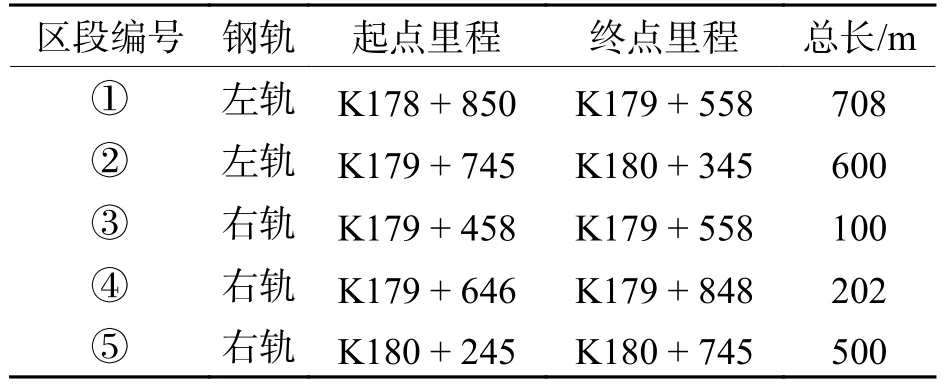
表1 异常区段里程定位信息Tab. 1 Mileage positioning information for abnormal section

图7 动态高低不平顺指定频带小波能量集Fig. 7 SWP of dynamic longitudinal unevenness

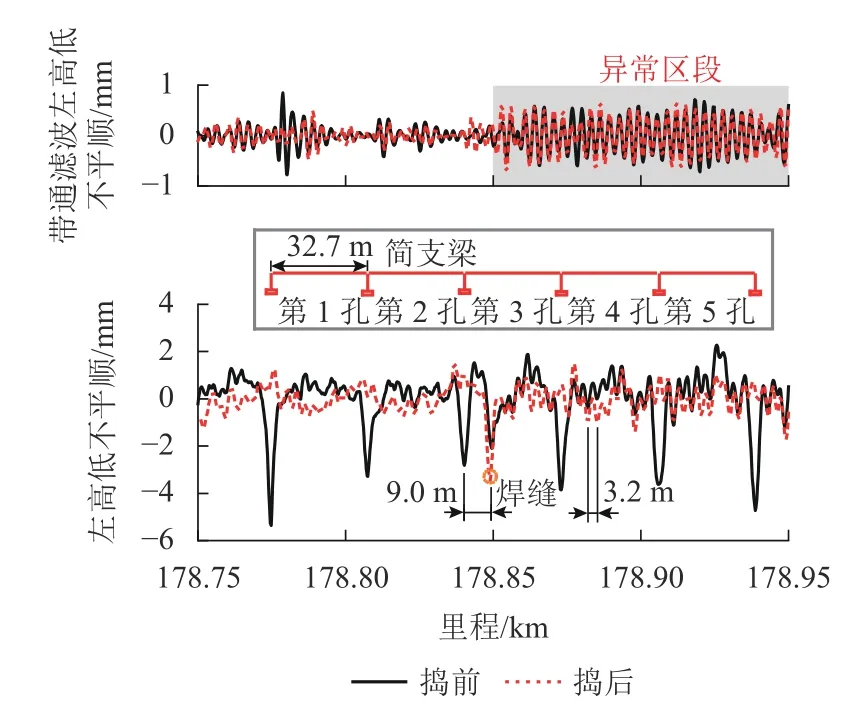
图8 异常区段 ① 起点处左高低不平顺Fig. 8 Left longitudinal unevenness at the starting point of abnormal section ①

2.3 周期性不平顺成因

钢轨现代化生产流程根据先后顺序分为“精炼”“精轧”“精整”“长尺化”“集中检测”[15].为满足高速铁路对钢轨平直度的要求，从“精轧”到“精整”的重要环节就是钢轨热预弯和平立复合矫直，热预弯改善钢轨矫前弯曲度，矫直是对钢轨进行往复弹塑性弯曲变形以提高钢轨平直度. 钢轨垂向矫直过程如图9所示. 钢轨在向左输送时，下排平辊水平支撑钢轨，上排平辊施加不同的压下量实现矫直效果，同一排相邻平辊的水平间距为1.6 m，上下两排平辊水平错开0.8 m. 异常周期性高低不平顺1阶主波长3.2 m，与平辊间距1.6 m的2倍相同，其2阶主波长1.6 m与平辊间距相同. 可能由于中间某个平辊压下量不匹配，相邻3个上排平辊组合作用使得钢轨在垂向产生波长为3.2 m的塑性变形，在钢轨矫直过程中产生的异常周期性不平顺，将此类不平顺命名为钢轨轧制不平顺. 根据《高速铁路用钢轨》（TB/T 3276—2011）[16]，钢轨在出厂前需进行轨身垂向平直度检测，尺长3.0 m平直度不超过0.3 mm、尺长1.0 m平直度不超过0.2 mm. 但这两种尺长均小于钢轨轧制不平顺主波长3.2 m，这可能是未能在钢轨出厂前发现此类缺陷的原因.

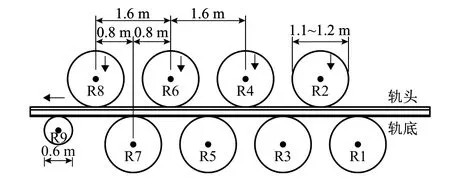
图9 钢轨垂向矫直示意Fig. 9 Schematic of rail vertical straightening

3 钢轨轧制不平顺对车辆动力学性能的影响

尽管该线钢轨轧制不平顺幅值并未超过《高速铁路有砟轨道线路维修规则（试行）》（TG/GW 116—2013）[17]中的Ⅰ级管理值（5.0 mm），但不良区段存在“抖车”现象，甚至还会引起车体垂向加速度超过Ⅱ级管理值（1.50 m/s2）[17]，严重影响旅客乘坐舒适度. 为进一步研究钢轨轧制不平顺对车辆动力响应的影响，下文采用实测车辆各部件振动加速度和轮轨力进行分析，试验列车为8节编组CRH2型动车组，车轮踏面为LMA型，钢轨廓形为60D，在分析前实现了高低不平顺与车辆动力响应信号的同步.

3.1 轧制不平顺与车辆动力响应的关系

功率谱密度能够表达响应在各波长处能量的分布情况，但不能得出输入与输出信号之间的对应关系. 相干函数用于评价系统输入与输出之间的因果性，借助相干函数可以分析轨道激励对车辆动力响应的影响，以此来确定与车辆动力响应密切相关的高低不平顺波长成分[18]. 将上述两种方法相结合，能够得到车辆动力响应在各波段内的能量分布和相干程度. 当功率谱密度和相干函数同为较大值时，可以认为该波长的高低不平顺对车辆动力响应愈加显著.

根据上行全线高低不平顺SWP筛选出存在轧制不平顺的区段，列车在不良区段车速波动未超过10 km/h，可以视为以242 km/h速度匀速行驶. 选取其中一段异常区段为分析对象，另取一段等长且车速同为242 km/h的正常区段为对照. 图10、11绘制了1.0～40.0 m波段内高低不平顺和车辆动力响应的功率谱和相干函数.

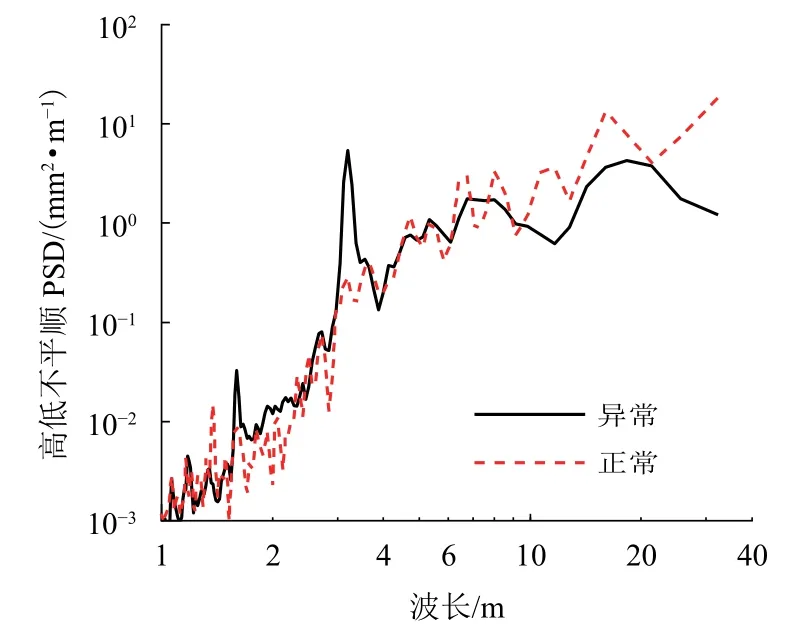
图10 异常与正常区段高低不平顺功率谱对比Fig. 10 Comparison of PSD between unevenness of abnormal and normal sections

从图10可以看出：在1.0～10.0 m波段内，异常区段高低不平顺功率谱存在两个谱峰，分别在1.6 m和3.2 m处，其余波长两者功率谱相当；波长大于10.0 m时，正常区段的高低不平顺功率谱整体要略大于异常区段，且随着波长的增大呈上升趋势.

从图11（a）看出：轴箱垂向加速度能量集中在0～6.0 m的短波范围，异常区段的1阶主波长和2阶主波长分别为3.2 m和1.6 m，均由轧制不平顺引起且明显大于正常区段. 3.0～11.0 m波段内轴箱垂向加速度受高低不平顺的影响最大，异常区段的1阶主波长3.2 m处相干函数从0.92增至0.97，说明轧制不平顺会放大轴箱垂向加速度的响应. 从图11（b）看出：构架垂向加速度功率谱特征和变化趋势与轴箱类似，能量集中在3.0～6.0 m的短波范围，异常区段的前2阶主波长也与轴箱一致.3.0～20.0 m波段内构架垂向加速度受高低不平顺的影响最大，异常区段1阶主波长3.2 m处的相干函数从0.77增至0.96，说明轧制不平顺对构架垂向加速度影响也非常不利. 从图11（c）看出：车体垂向加速度能量集中在3.0～6.0 m和10.0 m以上，轧制不平顺使得功率谱在3.2 m处达到最大值；与轴箱和构架不同的是，当波长大于9.0 m时，车体垂向加速度功率谱随着波长的增大而增大. 4.0～6.0 m和10.0～20.0 m波段内车体垂向加速度受高低不平顺的影响最大，当存在轧制不平顺时，3.2 m波长的相干函数从0.19增至0.76，说明轧制不平顺会显著加剧车体的垂向振动. 尽管波长为3.2 m的轧制不平顺对轴箱、构架和车体自下而上的影响越来越小，但当存在轧制不平顺时，三大部件的相干函数自下而上分别增长了5%、25%和300%，说明其带来的影响是自下而上越来越大的. 从图11（d）看出：轮轨垂向力能量集中在3.0～5.0 m和7.0、12.0、30.0 m处，轧制不平顺使功率谱在3.2 m处达到最大值. 同样是3.0～5.0 m波段内轮轨垂向力受高低不平顺的影响最大，异常区段1阶主波长3.2 m处的相干函数从0.66增至0.94，增长了42%，说明轧制不平顺对轮轨垂向力影响很大.

图11 车辆动力学响应功率谱及其相干函数Fig. 11 PSD and coherence function of vehicle dynamic response

3.2 轧制不平顺幅值的影响

高低不平顺和车辆动力响应都是包含多种波长成分的随机干扰函数，这种轧制不平顺是特征波长固定（3.2 m），为量化轧制不平顺对车辆动力响应的影响，需提取关注的特征成分再做处理. 首先采用截止频段为2.0～4.0 m带通滤波器对动检数据进行滤波，再计算滤波后信号移动RMS来分析其幅值和分布特征.

窗长的选取对分析结果影响很大，以往的研究表明采用滑动标准差进行统计分析时，其窗长应保证大于轨道不平顺波长的4倍[19]. 分析窗长的影响发现，窗长过短，不能够很好地将异常和正常区段分开；窗长过长，则无法清晰表达异常区段沿线路分布的严重程度. 经过比选，将12.0 m （特征波长的4倍）作为合理的分析窗长.

采用SWP筛选出车速在240 km/h附近的异常区段共计13 km，另选等速、等长度的正常区段作为对照. 图12给出了轧制不平顺RMS值和车辆动力响应RMS值的概率分布情况，发现两者均服从韦伯分布（Weibull distribution）. 正常区段高低不平顺和车辆动力学响应指标分布更为集中，沿纵轴方向看，正常区段占比最大值达到总数的15%～35%；异常区段占比最大值仅达到总数的7%～14%. 但正常区段占比最大值处对应的RMS值较低，沿横轴方向看，正常区段高低不平顺、车辆各部件振动加速度和轮轨垂向力RMS值集中在其最大值的16%～30%，而异常区段则集中在41%～47%.

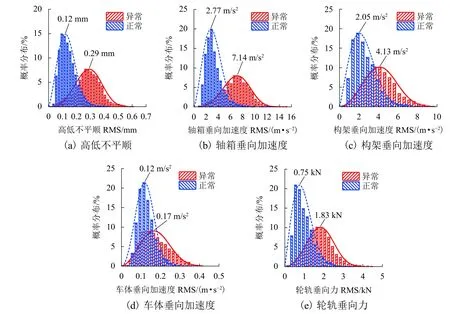
图12 轧制不平顺与车辆动力响应的RMS值分布Fig. 12 RMS amplitude distribution of straightening irregularity and vehicle dynamic response

图12 （a）还可以得出：异常区段的高低不平顺RMS值最大未超过0.65 mm，但大于0.55 mm的样本数量太少，不利于统计分析. 因此，将异常区段的高低不平顺RMS幅共分为5个区间：[0,0.15)、[0.15,0.25) 、[0.25,0.35)、[0.35,0.45)、[0.45,0.55) mm，分别代表高低不平顺RMS幅在0.10、0.20、0.30、0.40、0.50 mm处车辆动力响应的变化规律. 正常区段的高低不平顺RMS值最大值未超过0.45 mm，将其共分为4个区间.

图13给出了车辆动力响应RMS幅在各个高低不平顺RMS幅分布的箱线图，将各个响应RMS幅的均值点连线，用于表征车辆动力响应随高低不平顺的变化规律. 从图13（a）可以看出：两种工况的轴箱垂向加速度均随着高低不平顺的增大而线性递增. 在相同的高低不平顺下，轧制不平顺这种周期性特征会将轴箱垂向加速度RMS幅放大1.00 m/s2左右. 轴箱垂向加速度RMS幅的上、下四分位数相差不大，轴箱垂向加速度在各个高低幅值下的分布比较集中，说明轴箱加速度与高低不平顺之间存在较强的线性相关关系. 从图13（b）可以看出：异常区段的构架垂向加速度会随着高低不平顺的增大增速变快，正常区段的构架垂向加速度会随之增大增速变缓. 从图13（c）可以看出：两种工况的车体垂向加速度均随着高低不平顺的增大呈现逐级递增的趋势，但增速较缓. 在相同的高低不平顺下，钢轨轧制不平顺这种周期性特征会将车体垂向加速度RMS幅放大0.05 m/s2左右. 从图13（d）可以看出：两种工况的轮轨垂向力均随着高低不平顺的增大而线性递增.在相同的高低不平顺下，轧制不平顺这种周期性特征并未将轮轨垂向力放大. 轮轨垂向力RMS幅的上、下四分位数相差不大，说明轮轨垂向力与高低不平顺之间存在较强的线性相关关系.

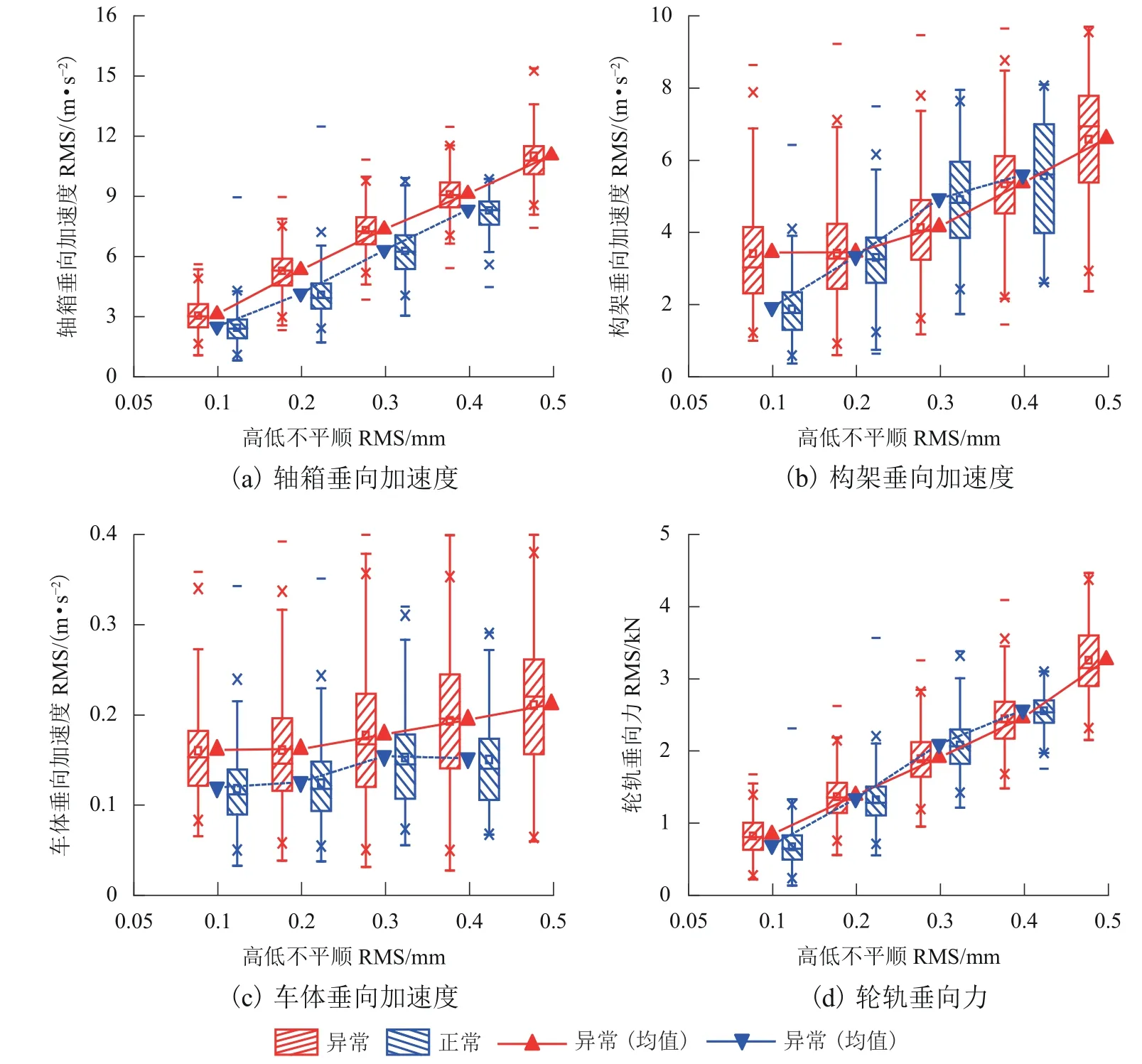
图13 车辆动力响应随轧制不平顺RMS幅的变化规律Fig. 13 Variation of vehicle dynamic response with RMS amplitude of straightening irregularity

前文发现轴箱垂向加速度和轮轨垂向力随高低不平顺幅值的增长大致呈现线性增长的趋势，分别对其作95%置信区间线形拟合，如图14所示. 图中：x为拟合直线的自变量，y为拟合直线的因变量. 由图14（a）可以看出：正常和异常工况的相关系数分别达到0.8和0.9，异常区段轴箱垂向加速度RMS值拟合直线均位于正常区段的之上，同样说明轧制不平顺这种周期性特征会将轴箱垂向加速度放大. 图14（b）可以看出：正常和异常工况的相关系数均达到0.8，说明轧制不平顺分别与轴箱垂向加速度和轮轨垂向力高度相关.

图14 轧制不平顺与轮对动力学响应的关系Fig. 14 Relationship between straightening irregularity and dynamic wheelset response

4 结 论

1） 由于钢轨在轧制过程中复合矫直工艺控制不良，引起钢轨轨身产生波长为3.2 m的周期性高低不平顺，继而导致列车发生“抖车”现象.

2） 在将动检数据进行同步压缩小波变换基础上，提出指定频带小波能量集（SWP）计算方法，利用这一方法能够真实反映钢轨轧制不平顺的分布特征.

3） 车辆动力响应与高低不平顺的相干分析结果表明，轧制不平顺使得轴箱、转向架、车体垂向加速度的相干函数分别达到0.97、0.96和0.76，较正常区段分别增长了5%、25%和300%；轮轨垂向力相干函数增长42%，达到0.94，说明轧制不平顺与车辆各部件的振动响应和轮轨接触力密切相关.

4） 车辆动力学指标RMS幅分析结果表明，轧制不平顺将轴箱和车体垂向加速度RMS幅分别放大1.00 m/s2和0.05 m/s2左右. 轧制不平顺与轴箱垂向加速度和轮轨垂向力RMS幅线性相关性最强，相关系数分别达到0.9和0.8.