基于统一强度理论的钢管自应力混凝土柱极限承载力研究*

蒙春贵 彭林欣,2 滕晓丹,2,3

(1.广西大学土木建筑工程学院， 南宁 530004； 2.广西防灾减灾与工程安全重点实验室，工程防灾与结构安全教育部重点实验室，广西大学， 南宁 530004； 3.广西新发展交通集团有限公司， 南宁 530028)

0 引 言

由于钢管混凝土具有承载力高、施工方便、耐火性能好等特点，已被广泛应用于高层、超高层建筑和桥梁工程中[1-3]。钢管混凝土的优越性能可归因于钢管与核心混凝土的复合作用[4]：钢管的约束提高了核心混凝土的强度和延性，核心混凝土的支撑作用使钢管稳定，延缓了局部屈曲。但普通的钢管混凝土在加载前中期，由于钢管的横向变形系数大于混凝土的横向变形系数，钢管对核心混凝土的约束作用不大；只有在加载的后期，约束作用才能得到体现[5]。为解决普通钢管混凝土柱前中期钢管约束效应不足的问题，利用自应力混凝土，补偿混凝土的收缩并在钢管约束下产生较高的自应力，使核心混凝土始终处于三向受压状态，提高构件承载能力。自应力混凝土是膨胀混凝土的一种，膨胀混凝土可以通过使用膨胀水泥或膨胀添加剂来制造，根据膨胀的大小，可分为补偿收缩混凝土[6]和自应力混凝土[7]，两者之间的主要区别是自应力混凝土的最终膨胀幅度更大[8]。

近年来，国内外学者对钢管自应力混凝土柱的力学性能开展了一系列研究。Li等[9]在核心混凝土中加固加入CaO基和MgO基膨胀剂，在恒定温度下以及在实际钢管混凝土结构典型变温历史下的变形和力学性能，分析CaO-MgO比的影响，结果表明膨胀剂的应用能有效地抑制钢管和混凝土的分离。Liu等[10]通过钢纤维自应力自密实混凝土柱的黏结试验研究，分析了不同混凝土类型、钢管壁厚、混凝土强度、钢纤维体积百分比对钢纤维自应力自密实混凝土柱黏结强度的影响，结果表明自应力能显著提高柱的黏结强度，钢纤维体积百分比的增加会使黏结强度先下降后上升，最后提出了钢纤维自应力自密实混凝土柱黏结强度预测公式。徐礼华等进行了钢管自应力自密实高强混凝土中长柱[11]和短柱轴压[12]试验，并基于极限平衡理论计算公式和试验结果，建立了钢管自应力自密实高强混凝土柱的轴压承载力计算公式，结果表明在钢管内浇筑自应力高强混凝土，不但可以补偿混凝土的收缩，而且钢管的侧向约束可以明显改善高强混凝土的脆性。李娜等[13]对圆钢管混凝土短柱进行轴心受压试验，根据极限平衡理论，考虑初始自应力的影响，提出了圆钢管自应力自密实混凝土短柱轴心受压承载力计算公式。

本文利用双剪统一强度理论，对钢管自应力混凝土轴压柱进行受力分析，引入考虑长细比的承载力折减系数，考虑了自应力对约束系数k的影响，推导了约束系数k的计算公式，构建了一种新的钢管自应力混凝土柱极限承载力理论计算方法。进一步分析了混凝土强度、钢材屈服强度、自应力值、钢管壁厚和钢管外径对该钢管自应力混凝土柱轴压极限承载力的影响，以期为今后钢管自应力混凝土柱的设计和应用提供参考。

1 双剪统一强度理论

双剪统一强度理论[14]是以双剪应力单元体为力学模型，考虑了中间主应力影响，能适用于各种不同材料，其表达式可为：

(1b)

赵均海[15]基于双剪统一强度理论，推导出钢管混凝土核心混凝土抗压强度的计算公式为：

-σ3=fc-kσ1

(2)

其中α=σt/σc

式中：σ1、σ2、σ3分别为第一、第二、第三主应力；α为材料的拉压比;σt、σc、τs分别为材料的拉伸屈服强度、压缩屈服强度、剪切屈服强度；b为反映中间主应力效应的材料参数，也是体现不同强度理论的参数,0≤b≤1；fc为单轴混凝土抗压强度；k为体现钢管对核心混凝土约束效应的系数。

2 钢管自应力混凝土柱承载力公式推导

钢管自应力混凝土柱由于混凝土的膨胀变形，使钢管在受荷之前处于环向受拉和纵向受拉状态，核心混凝土处于三向受压状态。由于管壁较薄，假设钢管环向应力沿壁厚方向均匀分布。设σsθ和σsz分别为钢管的环向拉应力和纵向拉应力，q为混凝土径向自应力，σcz为混凝土纵向反力。受荷前钢管和核心混凝土受力如图1所示。

a—钢管受力简图； b—核心混凝土受力简图。

钢管的环向应力σsθ和纵向应力和σsz可通过实测管壁的环向、纵向应变由胡克定律算得：

(3)

由材料力学知2rq=2tσsθ，径向自应力为：

q=tσsθ/r

(4)

式中：q为径向自应力；r为混凝土半径；t为壁厚；σsθ为钢管环向拉应力。

当钢管混凝土柱受到外荷载时，可设钢管混凝土柱的外径为D，半径为R，混凝土半径为r，壁厚为t，钢管的屈服强度为fs，钢管所受的环向拉应力为σθ，混凝土内压力和钢管对混凝土的侧向约束力互为作用力与反作用力，大小均为σr。对于普通钢管混凝土柱，当在极限状态时，钢管和核心混凝土受力如图2所示。

图2 极限状态时钢管受力图

对于钢管，已知：

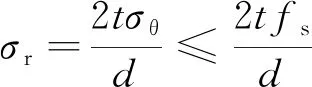
(5)

对于核心混凝土，受力状态为：0≥σ1=σ2≥σ3，且受压混凝土一般取压为正拉为负，式(2)变为：

σ3=fc+kσr

(6)

设钢管和混凝土协调变形：σ1=σ2=σr，式(6)变为：

σ3=fc+kσr

(7)

式中：σ3为核心混凝土抗压强度；fc为单轴混凝土抗压强度，核心混凝土为圆柱体，故fc为圆柱体单轴抗压强度；k为约束系数；θ为混凝土的内摩擦角，具体值由试验确定。

钢管自应力混凝土柱由于混凝土的膨胀作用，产生了径向自应力q，在受荷初期核心混凝土已处于三向受压状态，外荷载先平衡钢管纵向拉应力，在极限状态时受力状态与普通钢管混凝土柱相同。但径向应力比普通钢管混凝土柱大，其径向应力σr1大致为普通钢管混凝土柱在极限状态时的径向应力σr与径向自应力q的叠加，即：

σr1=σr+q

(8)

代入式(7)中得钢管自应力混凝土核心混凝土抗压强度算式为：

σ3=fc+k(σr+q)

(9)

钢管混凝土的承载力由钢管承载力和核心混凝土的承载力共同组成，故钢管自应力混凝土柱的承载力为：

N=Nc+Ns=σ3Ac+fsAs

(10)

参照规范[16]引入承载力折减系数φl：

φl=1L1/D≤4

(11a)

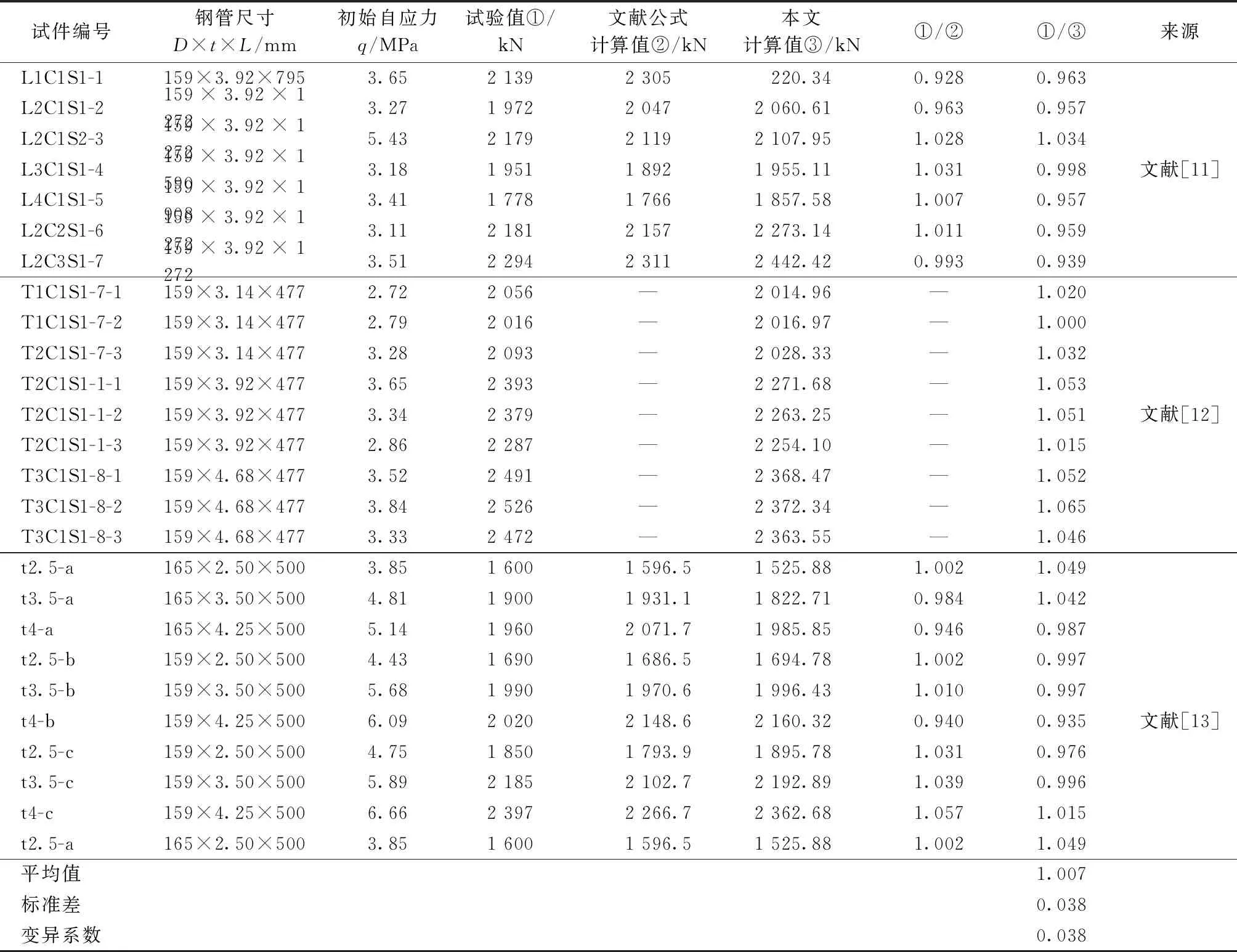
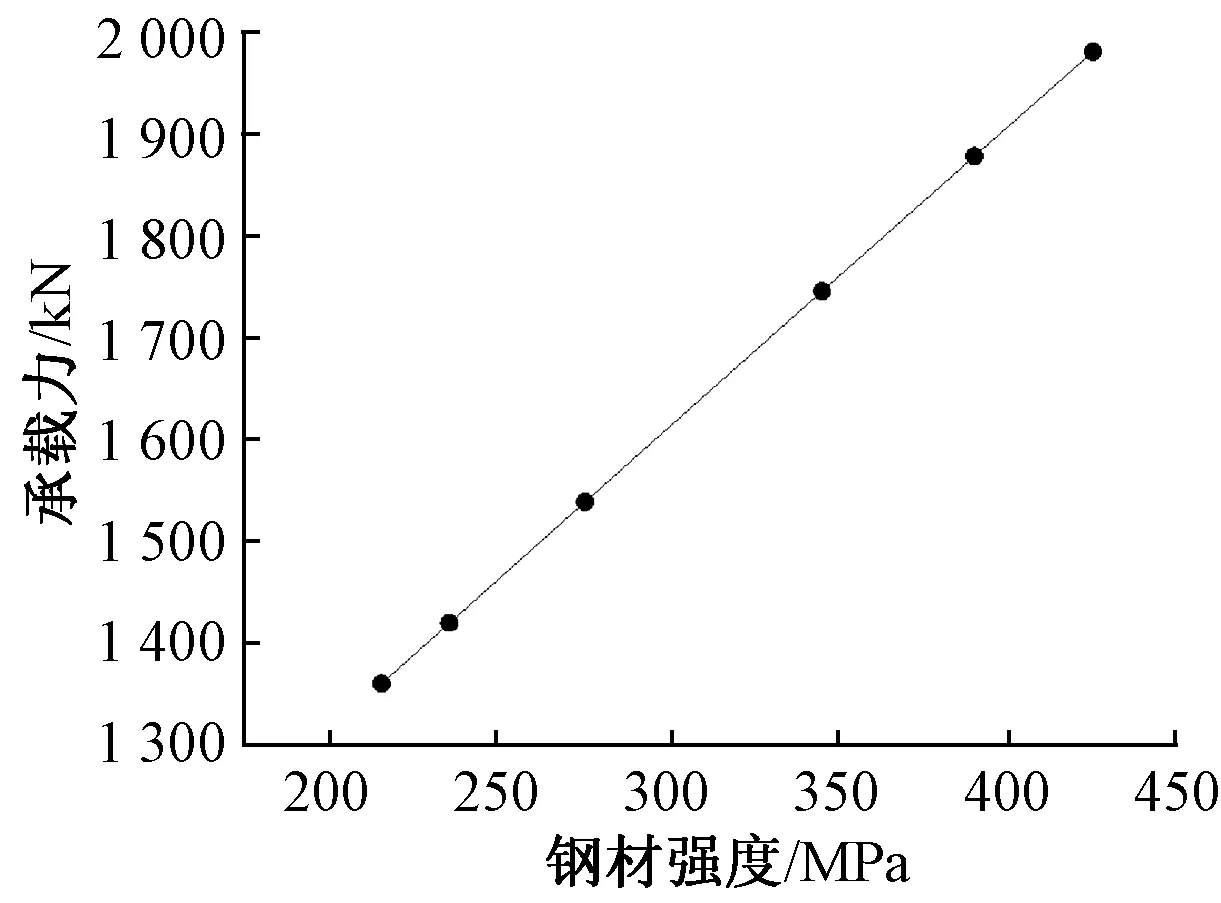
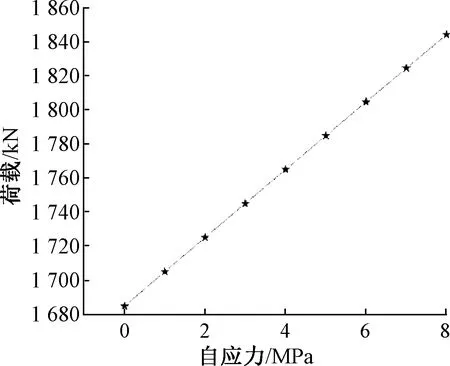
φl=1-0.022 6(L1/D-4)4

(11b)

当处于极限状态时取σθ=fs，径向应力：

σr=2tfs/d

(12)

将式(9)、(12)代入式(10)中并引入φl，整理即得式(13)，一种新的钢管自应力混凝土柱极限承载力计算方法：

Nm=φl(σ3Ac+fsAs)=φl[Acfc+Asfs+kAc(2tfs/d+q)]

(13)

其中Ac=πd2/4

As=(πD2-πd2)/4≈πdt

式中：Ac为核心混凝土面积；As为钢管面积。

约束系数k的取值一般由具体试验确定，史庆轩等[17]认为k值与核心混凝土受到的侧压力及混凝土强度有关，定义相对环向约束力Δp(Δp=p/fc，其中p为钢管提供的环向压应力，fc为混凝土单轴抗压强度)，并得到了约束系数k的计算式：

(14)

在本文中，钢管自应力混凝土处于极限状态时：p=σr+q，则考虑了混凝土自应力的约束系数k的新的计算式为：

(15)

利用以上考虑自应力的新的约束系数k的计算式，将自应力考虑到对径向侧压力的贡献中，从而提高核心混凝土的抗压强度。

3 计算方法验证

为说明本文计算方法的适用性，对文献[11-13]中钢管自应力混凝土轴压柱进行了分析计算，本文计算值与文献[11-13]试验结果对比如表1所示。

由表1可知，试验值与本文计算值比值平均值为1.000，标准差为0.038，变异系数为0.038。如图3为本文计算值与文献试验值对比。

图3 本文计算值与文献试验值[11-13]对比

表1 本文计算值与试验结果对比

通过与文献的钢管自应力混凝土轴压柱的试验结果对比，本文的理论计算值与文献中的试验值和公式计算值吻合良好，充分说明本文提出的钢管自应力混凝土柱极限承载力计算方法的合理、适用性。本文的计算方法过程简单，算式简便，算式中系数少，能准确地预测出自应力钢管混凝土柱的极限承载力。

4 钢管自应力混凝土轴压极限承载力的影响因素分析

为进一步研究各设计参数对钢管自应力混凝土柱轴压极限承载力的影响，取混凝土强度等级为C40，钢管外径为159 mm，壁厚为4 mm，长度为636 mm，钢材屈服强度为345 MPa，混凝土自应力值为3 MPa的钢管自应力混凝土柱为例，基于本文计算方法改变各设计参数分析轴压承载力的变化。

4.1 混凝土强度等级

当混凝土强度等级分别为C30、C35、C40、C45、C50、C55、C60、C65、C70、C75、C80，其余条件相同时，钢管自应力混凝土柱承载力变化曲线如图4。由图可知，随着混凝土强度等级的提高，柱的承载力接近线性增长。由数据可得：承载力的极差R=1 131.9，标准差S=350.8。

图4 混凝土强度对钢管自应力混凝土柱承载力的影响

4.2 钢材屈服强度

当钢材屈服强度分别为215，235，275，345，390，420 MPa，初始条件不变的情况下，钢管自应力混凝土柱承载力变化曲线如图5。柱的极限承载力随着钢材屈服强度的提高而提高，且接近线性增长。由数据可得：承载力的极差R=621.84，标准差S=231.3。

图5 钢材屈服强度对钢管自应力混凝土柱承载力的影响

4.3 混凝土自应力值

当混凝土自应力值分别为0，1，2，3，4，5，6，7，8 MPa，其余条件相同时，承载力变化曲线如图6。由图可知，随着混凝土自应力值的增大，柱的承载力也近线性增长。由数据可得：承载力的极差R=159.2，标准差S=51.4。当混凝土自应力值为0时，承载力为1 684.85 kN，当自应力值达到3 MPa时，承载力为1 745.02 kN，当自应力值达到8 MPa时，承载力为1 844.02 kN，自应力值为3 MPa、8 MPa较无自应力时柱的承载力提高分别为3.35%、8.63%。结果表明，提高自应力值能使柱承载力增加，采用自应力混凝土，使得混凝土与钢管在受荷初期能形成良好的黏结，核心混凝土从加载初期就受到钢管的套箍作用，提高了钢管与混凝土协同工作效率，故承载力相应提高。

图6 混凝土自应力对钢管自应力混凝土柱承载力的影响

4.4 钢管壁厚

当钢管壁厚分别为1，2，3，4，5，6，7，8，9 mm，初始条件不变的情况下，钢管自应力混凝土柱承载力变化曲线如图7。柱的极限承载力随着钢管壁厚的增大而提高，且接近线性增长。由数据可得：承载力的极差R=1 724.7，标准差S=556.1。

图7 钢管壁厚对钢管自应力混凝土柱承载力的影响

4.5 钢管外径

当钢管外径分别取90，100，110，120，130，140，150，160，170，180，190，200 mm，初始条件不变的情况下，钢管自应力混凝土柱承载力变化曲线如图8。由数据可得：承载力的极差R=1 801.5，标准差S=566.6。随着钢管外径的增大，钢管自应力混凝土柱的承载力相应提高，并且钢管的外径对该构件承载力的影响是五种因素(钢管外径、钢管厚度、混凝土强度、钢管强度和自应力)中最显著的。

图8 钢管外径对承载力的影响

5 结 论

本文基于双剪统一强度理论，从核心区混凝土所受侧向压应力的角度出发，分析不同状态时钢管自应力混凝土柱的受力状态，建立了钢管自应力混凝土柱承载力计算方法，并推导了考虑混凝土自应力的约束系数k值的计算公式，提高了承载力计算方法的适用性，经与试验结果的对比，验证了该方法的正确性。利用该计算方法进行参数分析，结果表明随着混凝土强度等级的提高、混凝土自应力值的增加、钢管直径的增大和钢管厚度的增大，钢管自应力混凝土柱的承载力都会提高。对于钢管自应力混凝土柱的承载力，各因素的影响顺序为：钢管直径>钢管厚度>混凝土强度>钢管强度>自应力，该结论为钢管自应力混凝土的优化设计提供了可靠的理论依据。