圆钢管约束陶粒混凝土短柱的单轴受压试验研究及承载力计算*

王宇航 赵玉婷 周绪红 李琦琦

(重庆大学土木工程学院， 重庆 400044)

0 引 言

陶粒混凝土作为混凝土材料领域的重大突破，是一种以陶粒代替一定比例粗骨料，结合胶凝材料、外加剂与水拌制而成的轻骨料混凝土[1]。该混凝土具有强质比高(强度高、质量小)、耐久性好、抗震性能优越以及环境友好的特点[2]；相同强度等级下，其表观密度相较于普通混凝土低20%～40%，工程造价可降低10%～20%[3]，符合近年建筑结构高耸，大跨的发展趋势[4]。但经研究，轻骨料混凝土的应力-应变全曲线呈现出上升段较缓、下降段较陡、残余强度较低[5-7]，以及不同时期泊松比均小于普通混凝土(υ=0.2)[8]的特点。可以看出，陶粒混凝土的弹性模量低，脆性特征显著[9-10]。因此研究如何提高陶粒混凝土的延性，充分利用陶粒混凝土的优点，具有重要的理论意义和实用价值。

钢管约束混凝土(Steel Tubed Concrete)充分发挥了钢材与混凝土两种材料的优势，是一种外包钢管主要用来为核心混凝土提供约束而不直接承担纵向荷载的组合柱[11-14]。研究表明，对于超短柱与短柱(L/D<4)，钢管可对核心混凝土产生较强的约束作用，从而较大程度地提高构件的承载力与延性[15-16]。在一定范围内，钢管屈服强度越高、径厚比越小，钢管约束混凝土短柱的轴压承载力越高[11,17-20]。由此可以看出，钢管约束混凝土的结构形式可以有效改善混凝土柱的脆性特征，提高构件承载能力。

经研究，外包钢管也可有效改善陶粒混凝土的延性。混凝土强度等级对于试件承载力的影响较小，增加配筋、降低径厚比可显著提高试件的极限承载力[21-24]。李帼昌等结合试验研究推导出了钢管约束下陶粒混凝土的本构关系与强度准则，吴东阳等则结合Samani等的研究成果，通过有限元模拟得到了圆钢管约束作用下核心陶粒混凝土的本构关系[25-26]。但以上研究均未考虑钢管与混凝土间摩擦等复杂因素对钢管约束陶粒混凝土轴压力学性能的影响，对于钢管约束陶粒混凝土承载力计算方面的研究也有待补充。

因此，本文对14个钢管约束陶粒混凝土进行轴压试验与理论分析，揭示了不同参数对钢管约束陶粒混凝土力学性能的影响，并结合承载力计算公式对试验结果进行对比分析。研究成果可为实际工程应用提供依据。

1 试验概况

1.1 试件设计与制作

试验设计并制作了 14个圆钢管约束陶粒混凝土短柱，主要参数为钢管屈服强度、径厚比、钢管与混凝土间的接触方式。按照钢管径厚比为13、19和30将试件分为3组。

钢管与混凝土间的接触采取对钢管内壁进行涂油(Oil)、贴聚四氟乙烯薄膜(PTFE)、聚氯乙烯薄膜(PVC)的处理方式。混凝土上下端部高于钢管10 mm，以确保钢管不直接承担纵向荷载。各试件设计参数见表1，试件尺寸见图1。

图1 试件几何尺寸 mm

表1 试件参数

1.2 材料性能

陶粒混凝土采用LC40的页岩陶粒混凝土，每立方米材料的用量分别为：水泥460 kg、页岩陶粒655 kg、河砂570 kg、硅灰40 kg、水155 kg、减水剂5 kg。根据GB/T 50081—2002《普通混凝土力学性能试验方法》与试件同条件养护28 d后，测试立方体试块抗压强度为47.8 MPa。

按照GB/T 228.1—2010《金属材料 拉伸试验：第一部分：室温试验方法》对钢管进行了拉伸试验，材料力学性能见表2。

表2 钢管材料特性

1.3 加载及测量方案

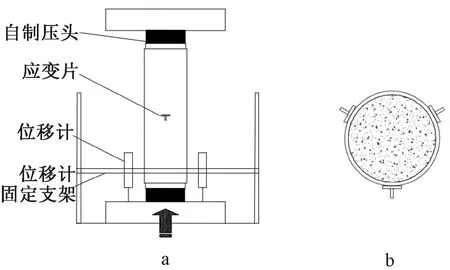
采用500 t液压试验机对试件进行轴压加载，加载装置见图2。试验采用分级加载方案：试验开始前需要反复预压对中。1 000 kN之前，加载速率为1.5 kN/s，持荷时间为1 min。在1 000 kN之后，控制加载速率为0.5 kN/s。并采用静态采集箱自动连续采集应变和位移数据。直至试件位移计示数到达60 mm或试件破坏，试验结束。

图2 试件加载及测量装置

整个过程中，环向间隔120°均匀布置三个竖向位移计记录竖向位移。跨中间隔120°布置环向和纵向应变片记录钢管应变，每个试件共计布置6个应变片，如图3所示。

a—钢管应变片布置立面； b—钢管应变片布置俯视。

2 试验结果及分析

2.1 试验现象

全部试件最终破坏形态如图4所示。在加载前期，试件均未见明显的破坏现象。加载至位移8 mm左右会产生页岩陶粒被挤压的声音，钢管与混凝土间用聚氯乙烯、聚四氟乙烯间隔开的试件会产生混凝土与内膜错动的声音，钢管无明显变形。加载至15 mm，上下端部混凝土发生溃烂、掉渣现象。加载至30 mm，距上下端部1/3处，外包钢管最终因为无法抵抗内部混凝土的膨胀及剪切破坏而屈服，导致环向鼓曲，如图5中黄框部分所示。试验临近结束，部分试件会产生侧弯，笔者分析有2点原因：1)加载过程中出现偏心受压；2)核心混凝土为非匀质材料，试件对混凝土进行轴压时，混凝土一旦产生非均匀破坏，在后续加载过程中会延续之前的变形情况，发展成为侧弯形态。

观察图4可以发现，降低径厚比，钢管与混凝土间填充薄膜，试件鼓曲越轻，说明上述方法增强了钢管对混凝土的约束作用。从图5和图6对比可以看出，试验结束时破坏试件端部的陶粒混凝土被压入钢管内，深度约10～40 mm。钢管屈服强度对试件破坏模式无显著影响。

a—D/t=30； b—D/t=19； c—D/t=13。

a—345-12-PTFE-LC； b—345-5-PTFE-LC。

图6 345-8-O-LC破坏模式

将破坏试件的钢管剖开，核心混凝土的最终破坏结果相似，均呈现出明显的剪切破坏。图5为试件235-12-PVC-LC 与345-5-PTFE-LC剖开示意，可以看出试件一半高度范围内存在一条明显的滑移斜裂缝，裂缝倾斜角度约60°。

2.2 钢管荷载-纵向变形曲线

各组试件的荷载(P)-纵向位移(Δ)关系曲线如图7所示。对于试件极限荷载取值方法，当轴向荷载-压缩变形有下降段时，取最大荷载；当轴向荷载-轴向压缩变形无明显下降段时，取轴向变形值为试件总高度1/15时(33.3 mm)对应的荷载或出现不适宜继续加载的终止加载点处对应的荷载[27]。其中纵向位移取3个位移计测得位移的平均值。

从图中可以看出，由于试件长径比较小且径厚比较大，上下端开口的情况下圆钢管约束轻骨料混凝土具有良好的塑性，荷载-位移变形曲线无明显下降段。

曲线存在三个阶段，第一阶段为弹性阶段，轴向变形随荷载值线性变化，刚度较大。第二个阶段为弹塑性阶段，刚度随着荷载逐渐降低。第三个阶段为塑性阶段，构件刚度趋于恒定，位移增长速度明显变快。图中前5 mm的荷载-位移曲线斜率较小是由于试验前在核心混凝土上下端部垫有海砂，初始加载时存在海砂被压实的过程。

对比图7可以看出径厚比越小，钢管屈服点出现的越晚，试件承载能力越高。说明径厚比越小，钢管对核心混凝土的约束效应越大，对承载力的提高越明显。同时可以发现钢管屈服强度越大，试件在后期承载力越高，轴压刚度则无明显变化。

a—D/t=30; b—D/t=19； c—D/t=13。

由图7c可以发现，弹性阶段钢管与核心混凝土间涂油的试件承载能力更高，加载至后期内部填充薄膜的试件承载力提高更显著。对于钢管与混凝土间涂油的试件，钢管与混凝土间的黏结摩擦更大，钢管承担较大的纵向力，因此前期承载力较大。对于钢管与混凝土间填充薄膜的试件，钢管承担的纵向力较小，对核心混凝土的约束作用发挥得更加充分，有助于改善后期钢管约束陶粒混凝土的延性，提高试件承载力。

2.3 钢管荷载-应变曲线

试件的荷载-应变曲线如图8所示，图中正向为纵向应变，负向为横向应变。

各组试件的钢管荷载-应变发展规律基本相同，横向应变与纵向应变较为接近，难以达到钢管不承担纵向荷载的理想约束状态。弹性阶段混凝土横向变形较小，钢管与混凝土间的相互作用较小，持续加载至弹塑性与塑性阶段，钢管与混凝土间的相互作用增强，钢管出现鼓曲，应变加速发展，曲线斜率变小。

对比图8可以发现：相同荷载水平下，径厚比越小，应变水平越低，荷载-应变曲线越光滑。D/t>19时，钢管屈服强度对应变无显著影响；当D/t≤19时，钢管屈服强度越大，应变越小。说明只有在径厚比较小(D/t≤19)时，屈服强度对于试件力学性能的改善作用才能充分发挥。

观察图8c可以发现：相同荷载水平下，当D/t>19时，接触对应变的影响不明显；D/t≤19时，钢管与混凝土间填充薄膜的试件应变水平低于钢管与混凝土间涂油的试件。这是因为此类结构形式下钢管被动受力，其应变滞后于混凝土应变，这种应变不协调导致钢管与混凝土间存在摩阻力，钢管与混凝土间填充薄膜可有效降低钢管与混凝土间的摩阻力，提高钢管对混凝土的约束作用，从而降低整体应变水平。

a—D/t=30； b—D/t=19； c—D/t=13。

2.4 钢管荷载-横向系数曲线

横向系数定义为试件轴压作用下的横向应变与纵向应变的比值，即：υc=εh/εv。式中εh和εv分别为同一级荷载下钢管的横向应变和纵向应变。相较于泊松比，横向系数可以更加真实可靠地反映不同阶段试件的变形特征。

观察图9可以发现，钢管的横向系数始终集中于0.1～3.0的范围。钢管的径厚比越大，横向系数越大且发展越不稳定,此时试件的鼓曲越明显，钢管对于核心混凝土的约束作用发挥越充分。钢管屈服强度越大，横向系数越大，钢管对混凝土的约束效应也越大。

a—D/t=30； b—D/t=19； c—D/t=13。

观察图9c可以发现，钢管与混凝土间填充薄膜的试件横向系数大于钢管与混凝土间涂油的试件。周绪红等的研究表明[19]，钢管约束混凝土在轴压受力过程中，核心混凝土最先受到压力产生变形，钢管由于变形协调的需要，在界面剪力的作用下纵向受力。界面剪力的来源有两点：1)固有黏结力，包含钢管与混凝土间的机械咬合力与胶结力；2)摩阻力，混凝土受压膨胀，钢管在界面产生摩阻力，表现为垂直方向的约束力。钢管与混凝土间填充薄膜，PTFE与PVC轻薄光滑，避免了钢管与混凝土的直接接触，可忽略固有黏结力，钢管与混凝土间的界面剪力主要由摩阻力产生。因此，此类接触可有效降低钢管的纵向受力，增强钢管对于核心混凝土的约束作用，从而提高试件后期承载力，虽仍达不到钢管不承担纵向荷载的理想状态，但可保证钢管与混凝土的协同变形，有利于构件在复杂工况下的受力性能。

3 单轴受压承载力计算方法

3.1 承载力分析

表3列出了各组试件的极限承载力，可以发现D/t≥19时试验极限承载力随着径厚比的减小而增大，D/t=13时，增大壁厚对于试验极限承载力提高并不显著。在本文的研究范围内，为充分利用钢管的约束作用，建议选取D/t≥19的构件用以工程实践。

对比表3可以看出，涂油试件的试验极限承载力大于钢管与混凝土贴膜处理的试件。结合图7，涂油处理的试件钢管与混凝土间摩擦力更大，钢管在加载初期承担较大的纵向力，因此初始刚度更大，前期承载力高。但后期钢管对混凝土的约束作用较弱，承载力提高较小。

表3 试验值与计算值对比

3.2 承载力计算公式

不考虑钢管与混凝土间接触对试件极限承载力的影响。约束区混凝土的抗压强度由非约束区混凝土的抗压强度fco和环向有效约束应力fr确定。本文采用Mander等[28]提出的轴心抗压公式：

(1)

由表4可知，试验极限承载力时，钢管已基本屈服。环向应力近似屈服应力，因此，钢管有效约束应力fr为：

(2)

则钢管约束陶粒混凝土短柱承载力计算公式如下：

Ne=fcoAc

(3)

式中：Ac为核心混凝土的面积；fco为核心约束混凝土的轴心抗压强度。

表3给出了本文公式计算结果与试验结果的对比，计算值与试验值之比的平均值为0.98，标准差为0.02，变异系数为2.1%。其中存在4组明显异常的数据，分别为：235-5-PTFE-LC，355-5-PTFE-LC、235-12-O-LC和355-12-O-LC。结合图4a可以看出，试件235-5-PTFE-LC与355-5-PTFE-LC存在明显侧弯,为偏心受压，试验极限承载力对应的横向应变远大于纵向应变，因此试验承载力与计算承载力误差较大。对于试件235-12-O-LC与试件355-12-O-LC，试验承载力均大于计算承载力，说明对于D/t≤19的试件，由于壁厚较厚，涂油处理无法有效降低钢管与混凝土间的界面剪力，钢管纵向受力较大,导致试件前期试验承载力较大。因此，对于D/t≤19的试件，建议采用钢管与混凝土间填充薄膜的接触方式，降低钢管纵向受力，提高试件后期承载力。

剔除异常数据后，计算值与试验值之比的平均值为0.97，标准差为0，变异系数为1.0%。可以看出采用Mander的计算模型可较为准确地计算圆钢管约束陶粒混凝土短柱的轴压承载力，计算结果较为保守。

4 结 论

本文对钢管约束陶粒混凝土短柱的单轴受压力学性能进行了试验研究和理论分析，并采用Mander模型对承载力进行计算，计算值与试验值拟合较好。主要结论如下：

1)钢管约束陶粒混凝土短柱在轴压荷载作用下上下端部1/3处发生明显鼓曲，剖开后混凝土呈现剪切破坏，剪切角约60°。降低钢管径厚比，钢管与混凝土间填充薄膜均可提高钢管对混凝土的约束作用，减轻鼓曲，改善破坏模式。

2)圆钢管约束陶粒混凝土短柱具有良好的塑性，荷载-位移曲线无明显下降段。D/t≥19时，钢管径厚比越小，试件承载力越大。钢管屈服强度越高，钢管与混凝土间贴膜，试件后期承载力提高越显著。

3)各组试件的横向应变与纵向应变较为接近。相同荷载水平下，径厚比越小，应变水平越低。当D/t≤19时，提高钢管屈服强度，钢管与混凝土间填充薄膜均可降低钢管应变水平，提高钢管对混凝土的约束作用。

4)钢管径厚比越大，屈服强度越高，钢管的横向变形系数越大。钢管与混凝土间填充薄膜的试件横向系数大于钢管与混凝土间涂油处理的试件。

5)基于Mander模型建议了钢管约束陶粒混凝土短柱轴压极限承载力计算公式，计算结果与试验结果吻合良好。