Weibull分布尺度参数变点的模型估计
程 静, 周菊玲
(新疆师范大学数学科学学院,乌鲁木齐 830017)
Weibull广泛应用在概率统计和可靠性分析中以及航空航天和生物医学的寿命检验上[1]. 周晓东等[2]用贝叶斯统计方法讨论并研究了删失数据下的Weibull分布参数问题;陈惠[3]在已知变点个数的情况下利用贝叶斯方法研究了Weibull分布的回归模型和变点问题;陈希孺[4]结合概率变点问题,介绍了极大似然估计方法、累计次数法和贝叶斯方法;程贝丽和周菊玲[5]利用极大似然法和贝叶斯方法研究了对数伽马分布变点模型的估计;何朝兵[6]通过添加缺损的寿命变量数据得到了在左截断右删失数据下Weibull 分布的完全数据似然函数,利用MCMC 法对该分布参数多变点进行了贝叶斯估计;师义民[7]就定数截尾样本讨论研究了Weibull分布三参数的贝叶斯估计;Meryem和Birgoren[8]利用极大似然估计方法和贝叶斯方法求解了材料的可靠寿命,蒙特卡罗模拟表明在相同的精度水平上,贝叶斯方法所需的样本量比极大似然估计方法更小. 温艳清和刘宝亮[9]利用N-R 算法、CM 算法及修正的CM 算法计算了完全数据下的Weibull 分布的极大似然估计,并分析了这三种算法处理问题时的优良性;戴迪昊等[10]参考数个气象台的样本数据,对最大风速序列的变点结合三参数的Weibull分布进行检验和估计. 乔世君和张世英[11]在定时截尾下,结合Gibbs抽样计算了Weibull 分布的贝叶斯估计,并且利用实际例子和经典的BLIE、BLUE 估计进行对比. 曾国桓[12]在定时截尾试验下对两参数威布尔分布的估计进行了研究. 李继政等[13]利用Weibull分布对极值波高进行研究分析,且选取贝叶斯方法和最大似然估计分别估计未知参数,最终从样本的拟合效果和设计波高计算两个方面分析这两种不同的估计方法所产生的效果. 对于Weibull分布变点的问题很少有人研究,本文利用极大似然估计和贝叶斯估计研究Weibull分布参数的变点估计问题,并通过随机模拟对这两种方法作比较.
1 Weibull分布单变点模型
设随机变量X服从Weibull分布,其分布函数和密度函数表达式分别如下:

其中:θ为尺度参数,η为形状参数,记为Weib(θ,η).
假设随机变量Xi(i=1,2,…,n)相互独立且满足
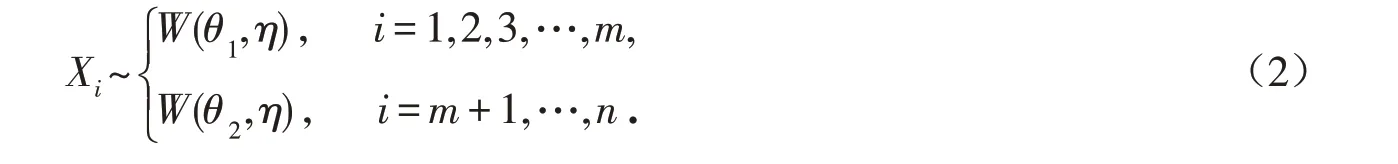
其中尺度参数θ1、θ2>0,且θ1、θ2、m都是未知的,当θ1≠θ2时正整数m就是要讨论的变点,该模型只有一个变点,称为Weibull分布尺度参数的单变点模型.
下面研究形状参数η为离散型随机变量时,Weibull分布尺度参数θ的单变点模型的极大似然估计和贝叶斯估计.
2 极大似然估计
设m为变点,当θ1≠θ2时,设X~Weib(θ,η),Xi(i=1,2,…,n)是总体的一个样本,其似然函数为:
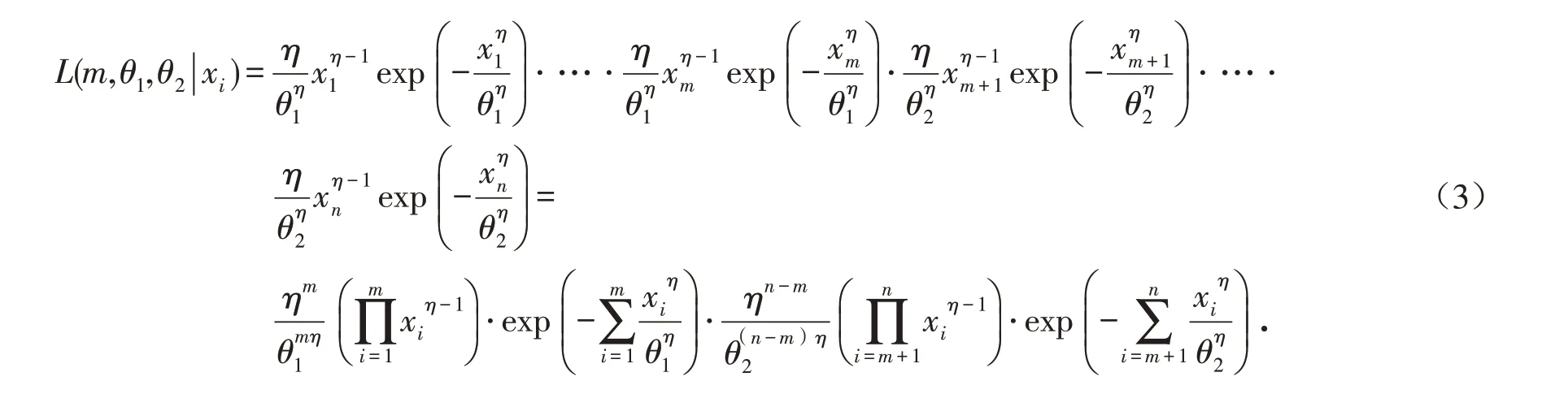
则对数似然函数为:

固定m,对θ1、θ2求极大,得:
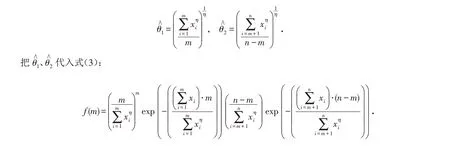

3 Weibull分布的贝叶斯估计
基于贝叶斯方法处理分布模型变点问题时,为了更好地得到统计推断结果,需引入先验分布,而选取先验分布一般通过分布的具体形式以及关于参数的历史数据信息,为此我们对m、θ1、θ2取如下先验分布:
1)对变点m取无信息先验分布:
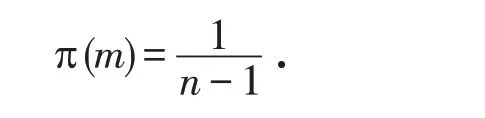
2)θ1、θ2的先验分布为逆伽马分布:
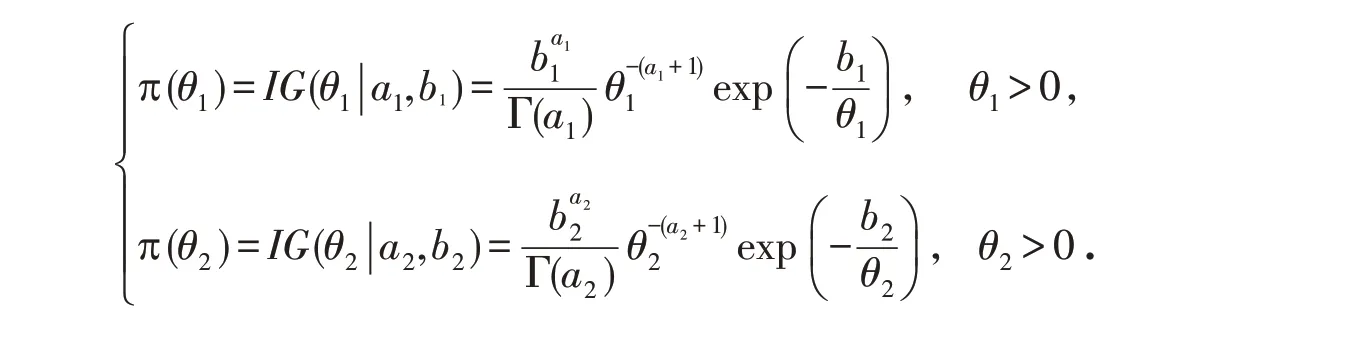
其中:a1>0,a2>0,b1>0,b2>0,m与θ1、θ2相互独立,则参数m、θ1、θ2的联合后验分布为:
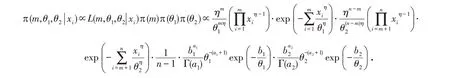
得到各参数的满条件分布:
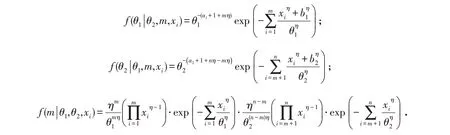
因为参数θ1、θ2的满条件分布形式比较简单,可以用Gibbs 抽样. 变点m的满条件分布较为复杂,用Gibbs抽样比较困难,所以我们在这可以利用M-H算法进行抽样. MCMC算法的具体步骤如下:


4 随机模拟
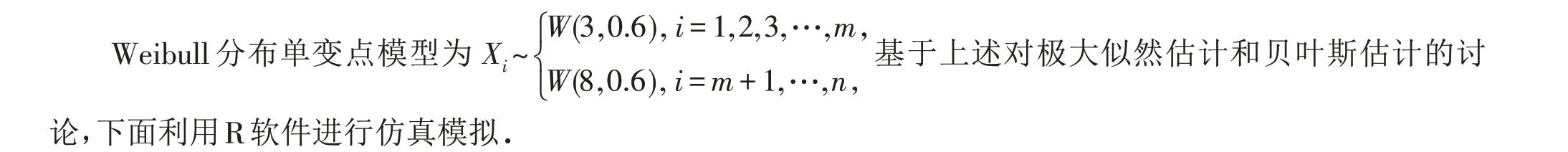
首先对极大似然估计进行模拟:
根据Weibull 分布的对数似然函数和极大似然估计式(5),利用R软件对未知参数m、θ1、θ2进行估计,结果如表1所示.

表1 参数m、θ1、θ2的极大似然估计Tab.1 Maximum likelihood estimation of parameter m,θ1,θ2
下面进行贝叶斯估计的随机模拟.
令n=200,取 参 数(m,θ1,θ2,η) 的 真 实 值 为(35,3,8,0.6),取M=20 000,B=10 000,根据参数m、θ1、θ2的满条件分布进行MCMC模拟,结果如表2所示.

表2 参数m、θ1、θ2的贝叶斯估计Tab.2 Bayesian estimation of parameter m,θ1,θ2
图1 是参数m的抽样迭代过程,从图中可以看出Gibbs 抽样波动较小,绝大多数在变点附近,即估计效果较好. 图2 是参数m的两条迭代链轨迹,可以看出这两条迭代链较稳定且逐渐重合,即收敛性比较好.
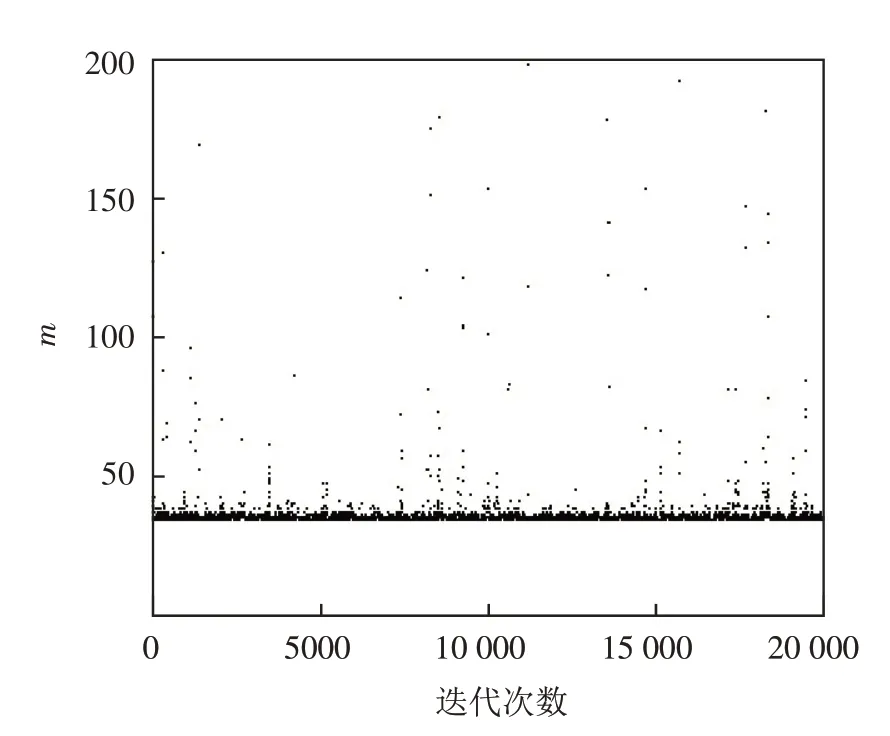
图1 参数m 的抽样迭代过程Fig.1 Sampling iteration process of parameter m
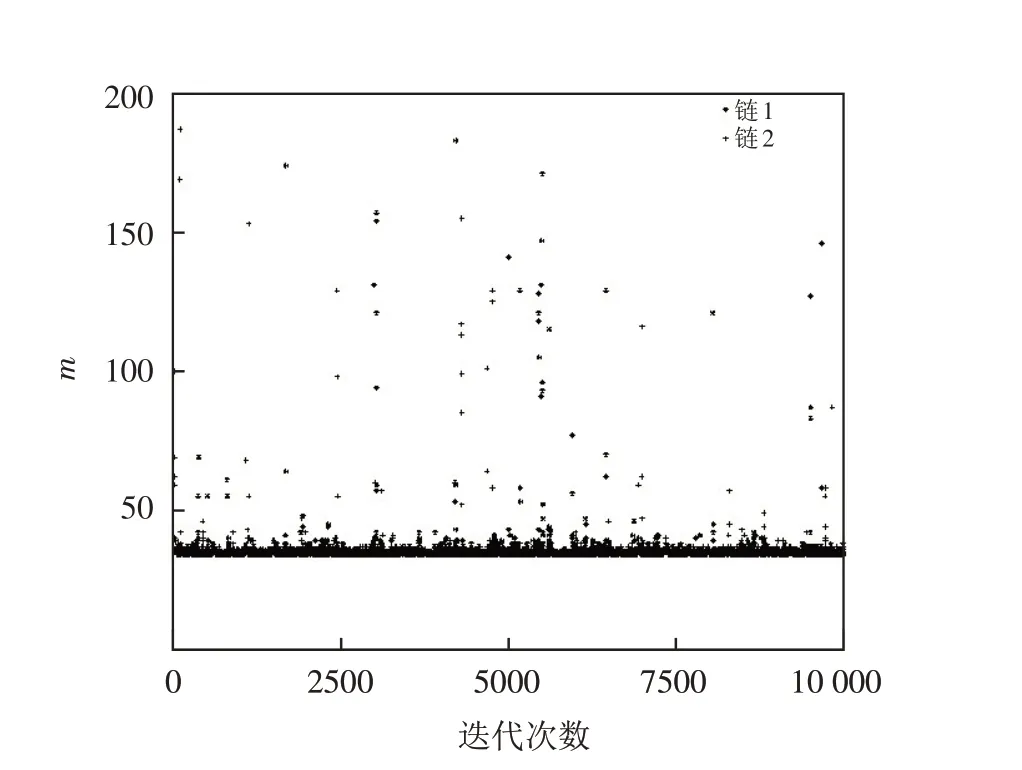
图2 参数m 的两条迭代链轨迹Fig.2 Two iterative chain trajectories of parameter m
从随机模拟结果来看,表1 中参数m、θ1、θ2的极大似然估计值与真值相差较大,精度不高;相比较表2三个参数的均值与真值差值较小,相对误差不超过6%,MC误差也较小,故整体上各参数的贝叶斯估计精度较高;各参数的标准差也比较小,说明数据比较稳定.
综上所述,Weibull分布参数的变点估计问题可以用MCMC方法实现,且估计效果都比较良好.

