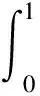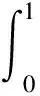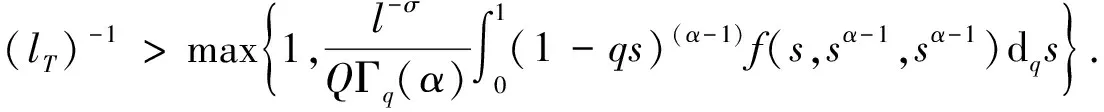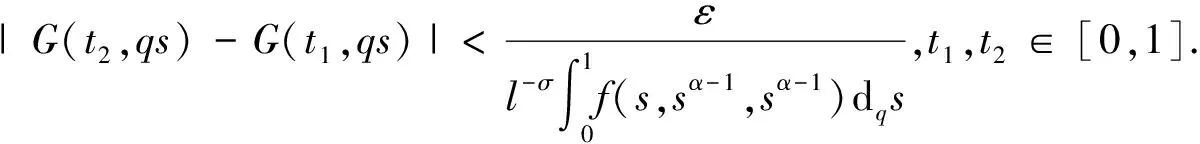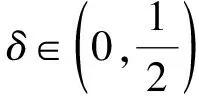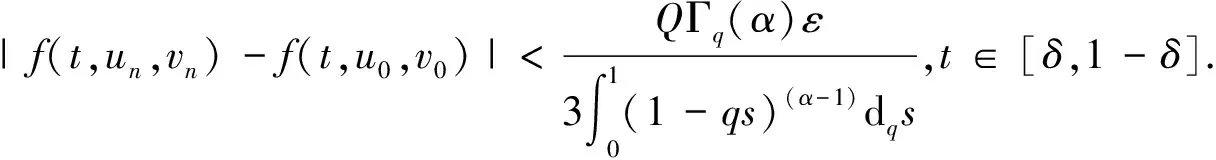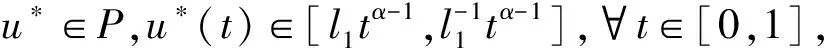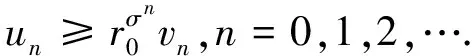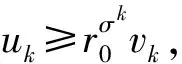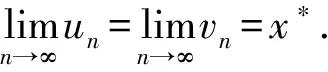一类非线性分数阶q-差分方程正解的存在性和唯一性*
胡紫寒, 张克梅
(曲阜师范大学数学科学学院,273165,山东省曲阜市 )
0 引 言
本文主要研究了以下具有分数阶q-差分的非线性边值问题
(1)
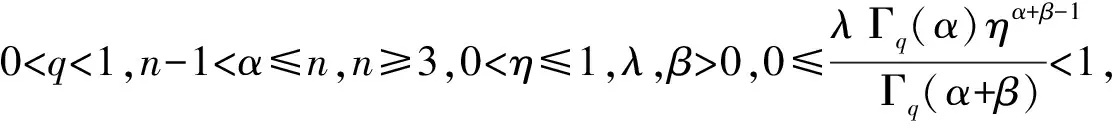
q-差分是一门古老的学科,它可以追溯到 Jackson[1,2]. 分数阶q-差分法来自 Al-Salam[3]和 Agarwal[4]. 目前,关于q-差分的研究有很多,此方面研究已被做了大量的工作[5-7].
在文献[8]中,考虑了以下分数阶q-差分Schrödinger方程
(2)
其中0 在文献[9]中,考虑了以下分数阶q-差分Schrödinger方程 (3) 其中0 在文献[10]中,考虑了一类带有非局部积分边值条件的非线性分数阶微分方程 (4) 本文运用了单调迭代方法和不动点理论,在一定条件下得到了问题(1)的最小最大耦合解;并在此基础上变换条件,运用单调迭代方法得到了问题(1)正解的唯一性. 关于本文,列出以下条件 (H1)f∈C((0,1)×[0,∞)×[0,∞),[0,∞)),其中(t,u,v)∈(0,1)×[0,∞)×[0,∞),f关于u是非增的,关于v是非减的,且存在一个正实数σ>0使得对任意的r∈(0,1],有 f(t,ru,r-1v)≥rσf(t,u,v). (H1′) 设条件(H1)中的其他条件满足,但其中σ满足0<σ<1,使得对任意的r∈(0,1],有 f(t,ru,r-1v)≥rσf(t,u,v). 注1.1由条件(H1)易知,对任意r>1,可得f(t,ru,r-1v)≤rσf(t,u,v). 本节中,将介绍一些符号和引理,它们将用于相关定理的证明. 定义2.1[5]设α>0,q∈(0,1)且f是定义在[0,1]上的函数.则函数f的Riemann-Liouville型的分数阶q积分定义为 定义2.2[5]设α>0,q∈(0,1).则α阶的Riemann-Liouville型分数阶q导数定义为 其中m是大于或等于α的最小整数. 引理2.3设α>0且p是一个正整数. 则下面的等式成立 引理2.4设y∈C([0,1],[0,+∞)).则以下边值问题 (5) 其中α∈(n-1,n],n≥3,n∈,0<η≤1,λ,β>0,有唯一解u(t)=G(t,qs)y(s)dqs,其中 证明由(5)式可知, 再由定义2.2和引理2.3,可知 c2=c3=…=cn=0, 将上式代入u(t)中,可得 则可得问题(5)的解为 当t≤η时,有 同理,当t≥η时,有 引理2.5定义在引理2.4的格林函数G(t,qs)满足以下性质 (1)G(t,qs)≥0,∀t,s∈[0,1]; (2)g1(s)tα-1≤G(t,qs)≤g2(s)tα-1,∀t,s∈[0,1],其中 当0≤qs≤t≤1,qs≤η时,有 G(t,qs)QΓq(α)Γq(α+β)=-QΓq(α+β)(t-qs)(α-1)+ Γq(α+β)(1-qs)(α-1)tα-1-Γq(α)λ(η-qs)(α+β-1)tα-1≥ -QΓq(α+β)tα-1(1-qs)(α-1)+Γq(α+β)(1-qs)(α-1)tα-1-Γq(α)ληα+β-1(1-qs)(α+β-1)tα-1≥ (-Q+1)Γq(α+β)tα-1(1-qs)(α-1)-Γq(α)ληα+β-1(1-qs)(α+β-1)tα-1≥ Γq(α)ληα+β-1tα-1{(1-qs)(α-1)-(1-qs)(α+β-1)}, 即 且有 G(t,qs)QΓq(α)Γq(α+β)=-QΓq(α+β)(t-qs)(α-1)+Γq(α+β)(1-qs)(α-1)tα-1- Γq(α)λ(η-qs)(α+β-1)tα-1≤Γq(α+β)(1-qs)(α-1)tα-1, 即 由此可知,当0≤qs≤t≤1,qs≤η时,G(t,qs)满足其性质,其他条件下,同理可得引理2.5成立. 在E中定义一个集合P如下, P={u|u∈C([0,1],[0,∞)),存在一个正常数0 定理3.1若(H1),(H2)成立,且存在一个正常数R>1使得 (6) 则分数阶q-差分方程(1)有最小最大耦合解(u*,v*)∈P,且存在常数0 且有单调迭代序列{un},{vn}如下: 证明显然,易知对任意的u,v∈E,有T:E×E→E. 下面证明算子T:P×P→P是全连续的. 首先,需要证明T:P×P→P. 由条件(H1)可知,算子T关于u是非增的,关于v是非减的. 对任意(u,v)∈P×P,由P的定义可知,存在一个正常数0 ltα-1≤u(t),v(t)≤l-1tα-1. (7) 通过引理2.5、(7)和条件(H1),可得 其中正常数lT满足 且 由(H2)可知 则算子T是良定义的. 综上可知,对任意(u,v)∈P,可得T(u,v)∈P,即算子T:P×P→P. 接下来证明算子T是全连续的. 令Ω是P上的有界集,存在一个正常数N>0,使得‖u‖,‖v‖≤N对任意的u,v∈Ω. 则由引理2.5 和(H2)可知, 因此可知,T(Ω)是一致有界的. 当u,v∈Ω时,对任意的ε>0,存在δ>0使得|t2-t1|<δ时,有 由以上条件可知 因此T(Ω)是等度连续的. 则由Arzela-Ascoli定理可知,T:P×P→P是紧的. 由f(t,u,v)在t∈[δ,1-δ]上的一致连续性和(un,vn)→(u0,v0),n→∞时,有 由以上条件可知 由上可知,算子T是连续的. 综上,T是全连续算子. 令PR={u|u∈P,‖u‖≤R},其中R满足(6)式. 下面证明T:PR×PR→PR. 由条件(H1)和(6)可知, 上式意味着‖T(u,v)‖≤R,因此,有T:PR×PR→PR. 令u0(t)=0,v0(t)=R,定义un(t)=T(un-1,vn-1)(t)和vn(t)=T(vn-1,un-1)(t),n=1,2,….由u0,v0∈PR和T:PR×PR→PR可知u1∈PR,v1∈PR. 由以上定义可知u1=T(u0,v0)=T(0,R)≥0=u0,通过归纳可知un+1≥un,un,vn∈PR,n=1,2,…. 由算子T的紧性可知{un}是相对紧集. 因此,存在u*∈PR使得un→u*,n→∞时. 同理,v1=T(v0,u0)=T(R,0)≤R=v0,通过归纳可知vn+1≤vn,un,vn∈PR,n=1,2,…. 由算子T的紧性可知{vn}是相对紧集. 因此,存在v*∈PR使得vn→v*,n→∞时. 由u0≤v0可知T(u0,v0)≤T(v0,u0),即u1≤v1,通过归纳,可得un≤vn,则有 u0≤u1≤…≤un≤vn≤…≤v1≤v0. 由上可得下式成立 u0≤u1≤…≤un≤…≤u*≤v*≤…≤vn≤…≤v1≤v0. 又由u*=T(u*,v*),v*=T(v*,u*),可知(u*,v*)是算子T在P×P上的耦合不动点. 下证(u*,v*)是算子T的最小最大耦合不动点. 设(u′,v′)是算子T在[u0,v0]×[u0,v0]中的任一耦合不动点. 于是u0≤u′≤v0,u0≤v′≤v0,假定n=k时,uk≤u′≤vk,uk≤v′≤vk,则有 uk+1=T(uk,vk)≤T(u′,v′)=u′≤T(vk,uk)=vk+1, uk+1=T(uk,vk)≤T(v′,u′)=v′≤T(vk,uk)=vk+1. 于是,根据归纳法,得un≤u′≤vn,un≤v′≤vn,则当n→∞时,有u*≤u′≤v*,u*≤v′≤v*.所以,(u*,v*)是算子T的最小最大耦合不动点,则分数阶q-差分方程(1)有最小最大耦合解(u*,v*). 定理3.2设(H1′),(H2)成立. 则问题(1)有唯一的正解x*(t)∈P,且对任意的u0,v0∈P,有 其中 证明由(H1′)中f(t,ru,r-1v)≥rσf(t,u,v)可知 (8) 由此可知T(rr-1u,r-1rv)=T(u,v)≥rσT(r-1u,rv),即 T(r-1u,rv)≤r-σT(u,v). (9) 令z(t)=tα-1,通过定理3.1可知T(z,z)∈P. 且令0 令 (10) 且 un=T(un-1,vn-1),vn=T(vn-1,un-1),n=1,2,…, 则有 u0,v0∈P,u0≪v0,u0=r0v0. 由(8)、(9)和(10)式可得 u1=T(u0,v0)≤T(v0,u0)=v1, 则通过归纳可知 u0≤u1≤…≤un≤…≤vn≤…≤v1≤v0. (11) 接下来,我们证明 (12) 则通过归纳总结,可知(12)式成立. 由(11)式和(12)式可知,对任意的自然数n和p*,可知 接下来,设y*(t)是(1)式的另一个正解,则存在一个正常数l*,使得l*tα-1≤y*(t)≤(l*)-1tα-1成立,其中l*∈(0,1),t∈[0,1]成立. 又因为r0足够小,则有u0(t)≤y*(t)≤v0(t),t∈[0,1],因T(y*,y*)=y*且算子T关于u是非增的,关于v是非减的,通过归纳总结可知 un(t)≤y*(t)≤vn(t),t∈[0,1]. (13) 当(13)式中n→∞时,可得y*=x*. 由上可知算子T有唯一的不动点x*,且对任意的u0,v0∈P,有 其中 un=T(un-1,vn-1),vn=T(vn-1,un-1),n=1,2,…. 综上,问题(1)在P上有唯一的正解x*(t),定理3.2成立.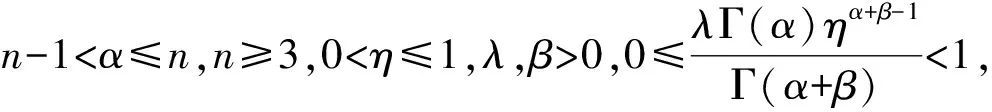
1 预备知识

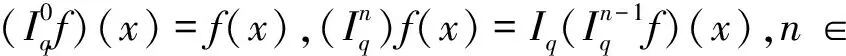
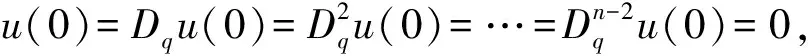



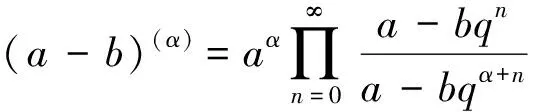
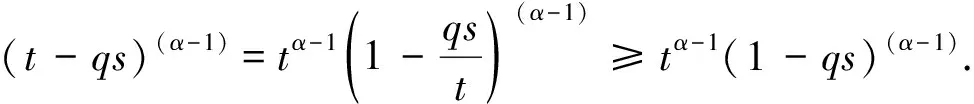
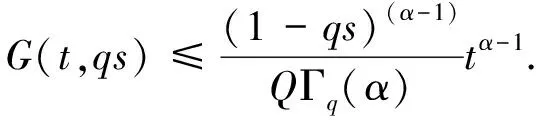

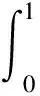
2 主要结论