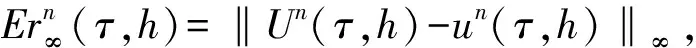RLW方程的高精度守恒紧致差分格式*
钟瑞华, 王晓峰, 宋 岩, 邓雅清
(闽南师范大学数学与统计学院,363000,福建省漳州市)
0 引 言
1966年,Peregine[1]在描述一个波形孔的发展时提出了正则长波(RLW)方程,该方程是非线性长波的一种表示形式,可以描述如浅水波和离子波等许多重要的物理现象. 目前对于RLW方程高精度差分法依然是近年来的研究热点之一. Bona[2]研究表明RLW方程解的存在性以及唯一性. 在限制初始条件和边界条件下,Wazwaz[3]给出了该方程的解析解. He[4]于1998年提出变分迭代法. Soliman[5]和Yusufoglu[6]分别在基于变分迭代法以收敛幂级数的形式和引入广义的拉格朗日乘子求解广义正则长波(GRLW)方程和RLW方程. 此外,王廷春[7]提出一种三层有限差分格式,在时间和空间上分别达到二阶精度并证明了格式的稳定性和收敛性. Kutluay[8]给出一种线性隐式有限差分方法得到RLW方程的数值解. 潘新田[9]对RLW方程提出一个守恒的三层差分格式,分析了格式的稳定性与收敛性,其收敛阶为O(τ2+h2). Zheng[10]提出一种新的Crank-Nicolson有限差分守恒格式,通过理查森外推法使得收敛阶达到O(τ2+h4). Wang[11]等人提出两种四阶守恒紧致有限差分格式求解RLW方程,分别为两层非线性和三层线性紧致差分格式,并证明了离散质量和能量的守恒性.
本文考虑如下RLW方程的初边值问题[7]
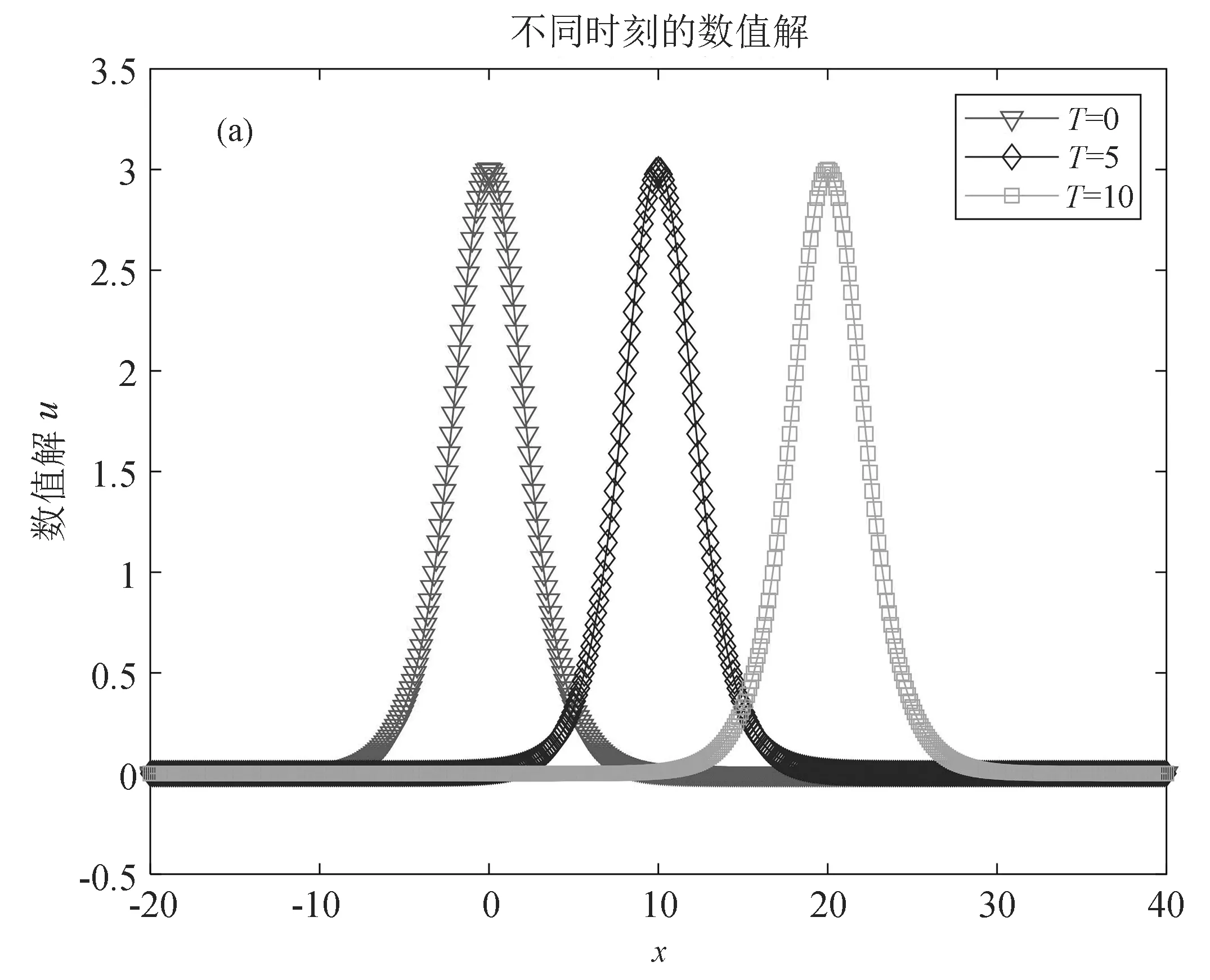
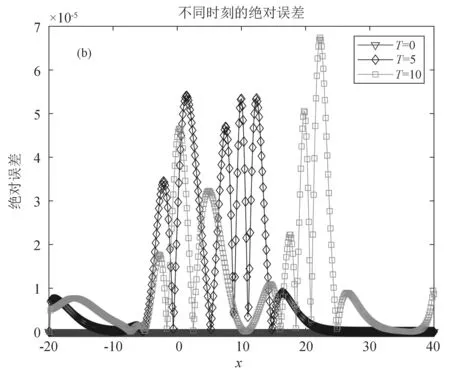
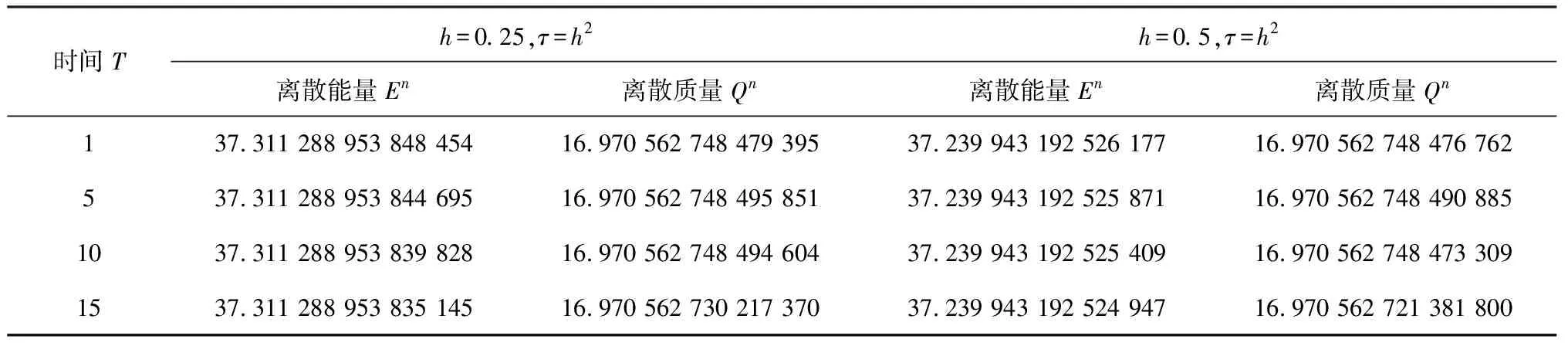
ut+εuux-μuxxt+ux=0,0 (1) u(x,0)=u0(x),α≤x≤β, (2) u(α,t)=0,u(β,t)=0,0 (3) 其中μ和ε是给定的正常数,且当x→±∞时,有u→0. 可以验证,问题(1)~(3)具有如下守恒律 (4) (5) 对求解区域[α,β]×[0,T]进行网格剖分,取空间步长h=(β-α)/J,时间步长τ=T/N,其中J,N为正整数,记网格点xj=α+jh(0≤j≤J),tn=nτ(0≤n≤N). 记 (6) (7) 对式(6)两端对x求二阶导数得 (8) 将式(8)代入式(7)可得 (9) 对式(9)应用如下二阶Taylor展开式 及在时间层上作平均,忽略截断误差项可得如下差分格式 (10) (11) (12) 由于格式(10)~(12)为三层线性隐格式,需求解u0和u1来启动计算,因此本文选取方程(11)和如下四阶两层线性格式来计算u1: (13) 证明对式(10)两边同时乘以h,并对j从1到J-1求和可得 由边界条件(12)整理可得 对上式作递推即可得Qn=Qn-1=…=Q0. (14) 由定义的差分算子和引理1,有 从而式(14)可以写成 (15) 把式(14)的n替换成l,并将l从1到n累加可得 故式(15)对n作递推即可得En=En-1=…=E0. 定理2差分格式(10)~(12)是唯一可解的. 证明根据式(11)可知u0,再用格式(13)计算u1,可知u0和u1是唯一确定的. 设u0,u1,…,un(n≤N-1)是唯一确定的,考虑式(10)中的un+1,则有 将上式与un+1作内积,且当h足够小使得1-h2/12>0时,有 即‖un+1‖=0,则差分格式(10)~(12)是唯一可解的. 证明令en=Un-un,则可得如下误差方程 (16) (17) (18) (19) 应用Cauchy-Schwarz不等式[13]和引理2,有 (20) (21) (22) 将式(20)~式(22)代入式(19)得 (23) 其中M0=min{1,μ(1-h2/12)}>0,则式(23)可以写成 (24) 对式(24)从1到n求和,对于h充分小,可得 即 其中 若τ和h充分小,使得M1=1/(1-Cτ/M0)>0,则 由离散Gronwall不等式[12]可得 An≤CM1(τ2+h4)2exp(CTM1/M0)≤C(τ2+h4)2, 考虑初始条件为[1]u(x,0)=3dsech2[k(x-x0)].则方程(1)精确解为 选取ε=1,μ=1,d=1,x0=0, 取h=0.05,τ=0.125,T=1和h=0.5,τ=h2,T=10,误差收敛阶的结果见表1和表2,分别验证了差分格式(10)~(12)在时间和空间上分别具有二阶和四阶的收敛精度. 该数值结果与理论分析结果一致. 表3验证了该格式的离散质量守恒以及能量守恒性. 取h=0.125,τ=h2在不同时刻的数值解和误差图,分别见图1(a)和图1(b). 图1和表3可见格式是稳定的. 以上结果表明所提的差分格式(10)~(12)的理论分析是有效可靠的. 表1 取不同时间步长时误差和收敛阶 表2 取不同时间和空间步长时的误差和空间收敛阶 图1 不同时刻的数值解和绝对误差 表3 取不同步长不同时刻下的离散守恒量1 差分格式的构造

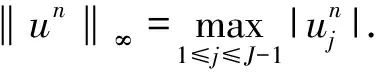
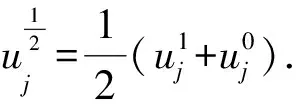
2 差分格式的守恒性和唯一可解性

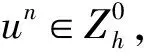
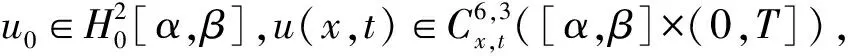
3 差分格式解的收敛性与稳定性
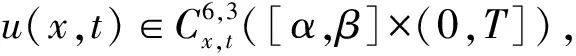

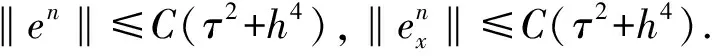
4 数值算例