暗室条件下强干扰信号多径效应对调零天线导航接收机测试影响分析

王雷钢，乔会东，周继航，王建路

暗室条件下强干扰信号多径效应对调零天线导航接收机测试影响分析

王雷钢，乔会东，周继航，王建路

（中国人民解放军63892部队，洛阳 471003）

在有限暗室条件下对自适应调零天线导航接收机进行抗干扰试验时，强干扰测试信号的多径反射功率经吸收、衰减后仍远大于导航信号，其是否影响调零天线抗干扰性能评估是决定测试可信度重要因素。基于多径下天线阵信号接收模型，通过对接收信号协方差矩阵分析，量化分析了多径信号引入与特征值、特征向量之间的关系；然后基于最小功率的调零模型，仿真验证了多径信号对调零天线权值造成的影响。结果表明，当干扰与其多径信号强度差小于一定值，天线阵零陷点会被从实际干扰来向点拉偏；但随着强度差增大，多径信号的引入对零陷点位置影响逐渐减小。

自适应调零天线；暗室；协方差矩阵；多径效应

0 引言

采用自适应调零天线的导航接收机是当前及未来主要卫星导航装备之一，其抗干扰能力敏感于干扰数量、来向分布等因素，如何构建出逼真立体的干扰信号环境，是实现对该类接收机客观测试的前提。辐射式导航暗室具有干扰信号环境构设可控易控、遍历充分、成本低等优势，是完成携带自适应调零天线导航接收机测试的重要手段之一。

在暗室环境中进行导航接收机抗干扰能力测试时，在有限的暗室尺寸和材料吸波能力条件下，干扰天线辐射出的干扰信号一部分直达天线口面，一部分则经吸波材料反射后以多径的形式到达天线口面。卫星信号强度到达天线口面通常约 -130 dBm，当前调零天线导航接收机抗干扰能力已达120 dB，当以此为准产生干扰信号时，天线口面直达干扰强度为-10 dBm，即使综合考虑暗室静区性能、极化隔离等因素，最强多径反射信号到天线口面功率仍会高于卫星信号。该多径信号是否影响暗室内调零天线抗干扰能力测试是需要明确的问题，具体而言即：该多径信号是否被视为新的干扰而降低调零天线的自由度，是否改变零陷位置和深度，从而影响测试结果的客观性。

当干扰及其多径信号引入到暗室内自适应调零天线的导航接收机时，其数学本质即为相干信号的处理问题。协方差矩阵是反映接收机接收信号关系一个重要变量，当前主要且工程化的一些自适应调零原则中，如基于最小均方误差、最大信干噪比、最小功率等[1]，所建立的优化目标均与协方差矩阵相关。各种原则虽基于不同前提约束以适用不同场合，但对稳态信号，所得的最优权均收敛于与协方差有关的维纳解[2]。因此，以协方差作为多径效应对调零天线导航接收机测试影响研究对象，具有较强的普适性。

为此，本文首先介绍了天线阵列信号接收模型和自适应调零模型，然后以此建立了多径干扰下的天线阵信号接收模型，推导接收信号协方差矩阵的特征值与特征向量，分析有无多径情况下协方差矩阵特征的差异性，以及这种差异性如何影响调零天线零陷数量、深度、位置等；最后采用功率倒置（Power Inverting，PI）算法进行了仿真，分析了多径对调零天线的影响。本文结论为在暗室内开展强干扰条件下自适应调零天线抗干扰测试的可行性、可信度提供理论支撑。

1 理论基础

文中所采用的符号说明如表1所示。

1.1 天线阵信号接收模型

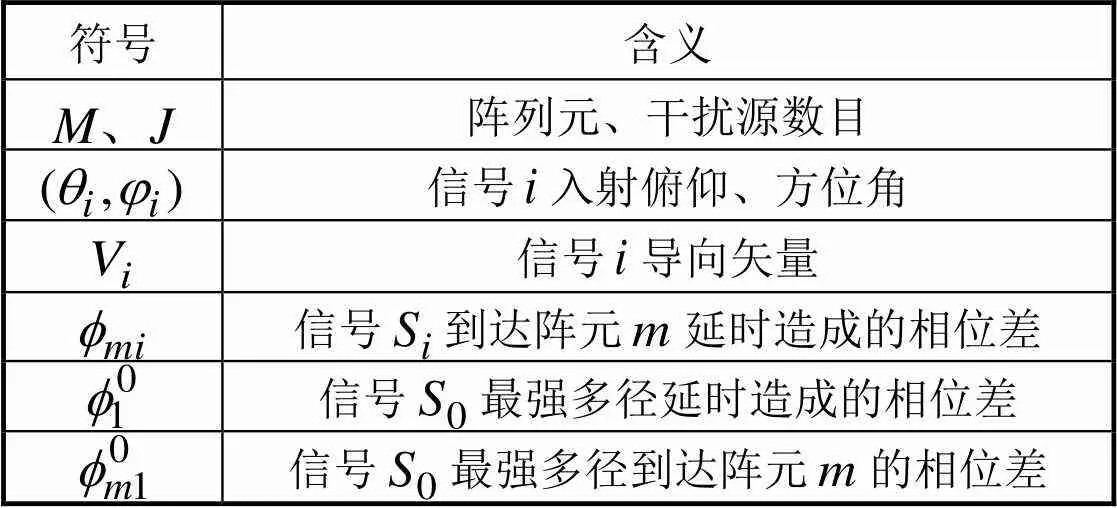
表1 文中主要采用符号定义

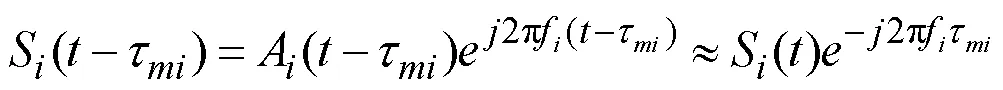
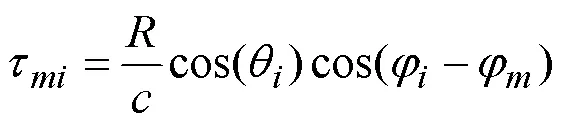
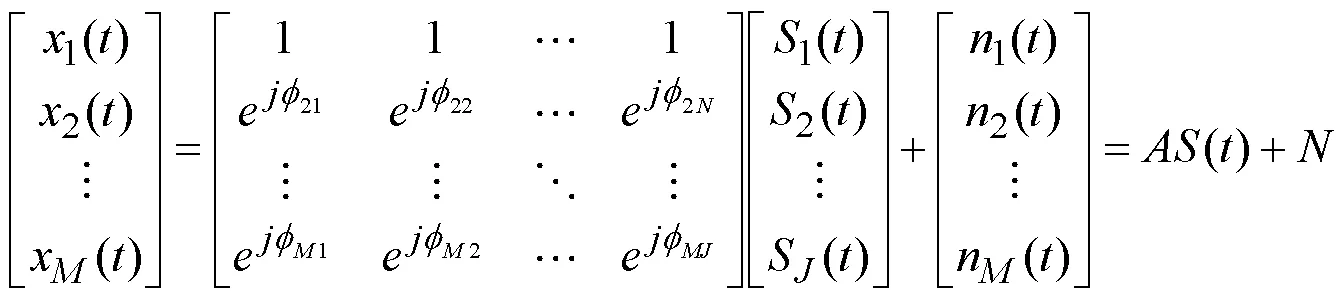
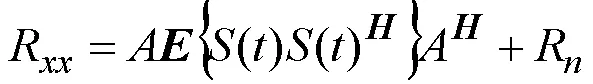
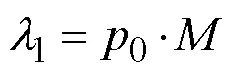
1.2 自适应调零模型

1.2.1 天线阵输出信号模型

自适应调零天线主要是对多个阵元接收到的信号进行处理，获得满足一定准则的合成信号输出于导航接收机。其过程一般是先采用一定的准则构建目标函数，然后通过优化处理算法，获得对各路输出采信的权值，并对此进行合成，合成后的输出模型可表示为：

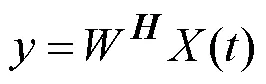
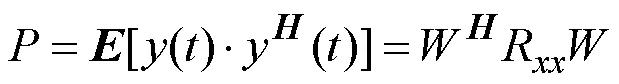
1.2.2 PI加权值优化

PI是一种实用的自适应调零天线权值优化原则，其优化目标是经处理后输出的信号功率最小，同时为保证优化后的权值不为零引入一线性约束，其优化目标函数为：

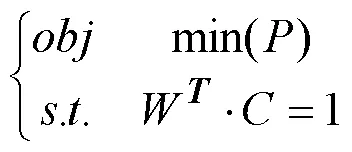
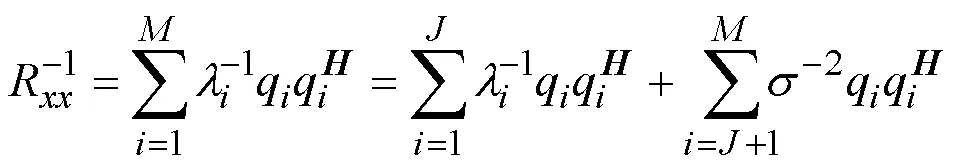
2 多径影响推导与分析

2.1 多径干扰下的天线阵信号接收模型

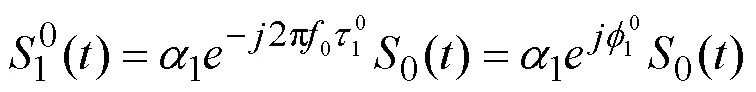
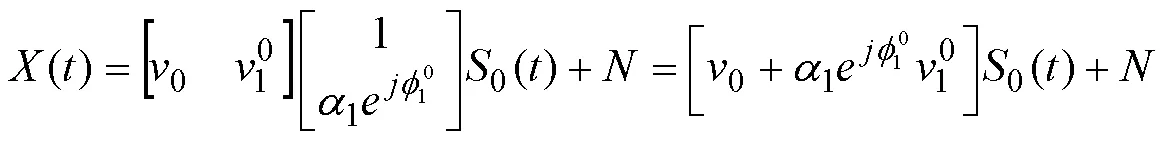
令：

则式（14）可进一步写为：

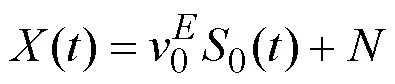
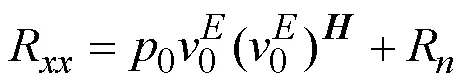
由此可见，在多径情况下，信号协方差矩阵仍只存在一个非零特征值，其值如式（20）所示：

2.2 多径影响分析

通过式（7）和式（20）对比，式（4）和式（18）对比，可得以下结论：

3 仿真验证

仿真采用4元Y型阵天线，调零权值算法采用最小功率准则。仿真基本参数设置为：接收机带宽2 MHz，卫星信号到达天线口面功率-130 dBm，载噪比45 dBHz。干扰采用噪声调频样式，干扰直达到天线口面功率-10 dBm。分无多径干扰（信号不同频、不同向）和有多径干扰（信号同频、不同向）两种情况分别进行仿真。

1）无多径时的干扰设置

设置三个频率不同、来向不同的干扰，参数设置如表2所示。

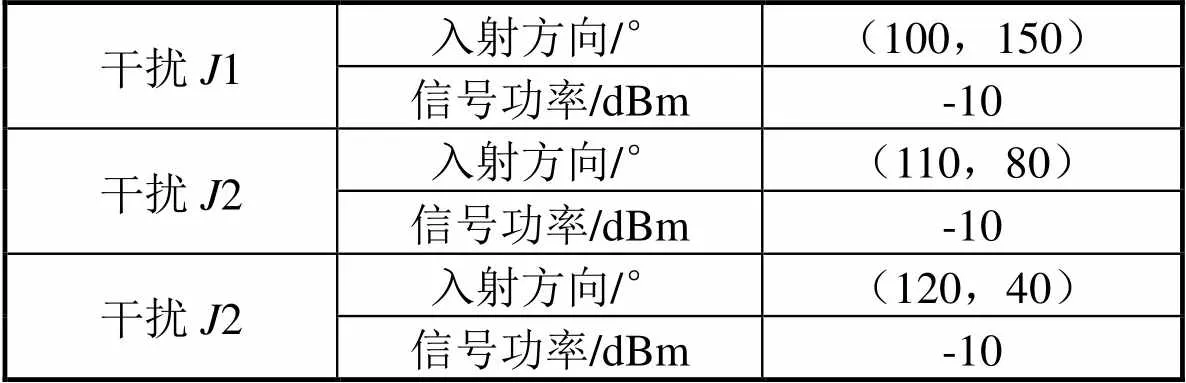
表2 干扰信号设置

接收信号的协方差矩阵存在三个特征值如表3所示，对应于三个不相干、不同向的干扰，方向图如图2所示，形成零陷与设置的干扰来向完全一致。说明在互不同向、互不相干的干扰下，调零天线能够在干扰入射方向正确地形成凹陷，干扰可以被明显地区分出。

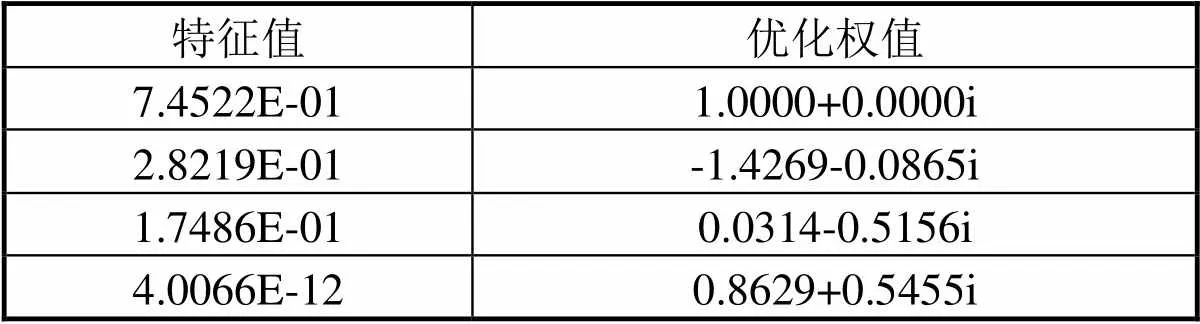
表3 特征值及优化权值结果数据

图2 三个不同频、不同向干扰下阵列增益图

2）有多径下的干扰设置

假设第一多径信号为2，信号1、2入射方向（120°，40°）、（100°，80°），相对于直达干扰信号1。

在不同功率差下，接收信号协方差矩阵的特征值如表4所示，可以看出当信号强度差超50 dB后，特征值基本不再发生变化。

信号1、2在不同强度差异下，自适应调零天线方向图如图3所示，可以看出当1、2强度差为20 dB时，如图3（a）所示，方向图零陷点从（120°，40°）被拉偏到（126°，57°），多径对方向图有影响；当1、2强度差达50 dB时，如图3（b）所示，零陷点回归至干扰信号入射方向（120°，40°），多径几乎对自适应调零天线方向图没有影响。

表4 接收信号协方差矩阵的特征值

图3 J1、J2强度差分别为20 dB、50 dB时自适应调零天线方向图

为验证直达、多径信号绝对功率对调零天线方向图的影响，将1信号强度设为-40 dBm，2信号强度设为-60 dBm（与图3（b）相同）。此时，方向图如图4所示，与图3（b）对比可知，零陷深度变浅，但由于1、2差较小，所以多径拉偏现象仍然存在，因此说明方向图零陷点位置与干扰1、2强度绝对值无关，而是由二者相对值所决定。

图4 信号功率J1=-40 dBm，J2=-60 dBm情况下自适应调零天线方向图

两路多径信号从不同角度入射情况下的自适应调零天线方向图如图5所示，信号功率分别为1=-10 dBm，2=-80 dBm，3=-90 dBm，对比图3（b），可见当直达和最强多径差达到一定程度后，若增加多径数量，方向图零陷位置点无变化。

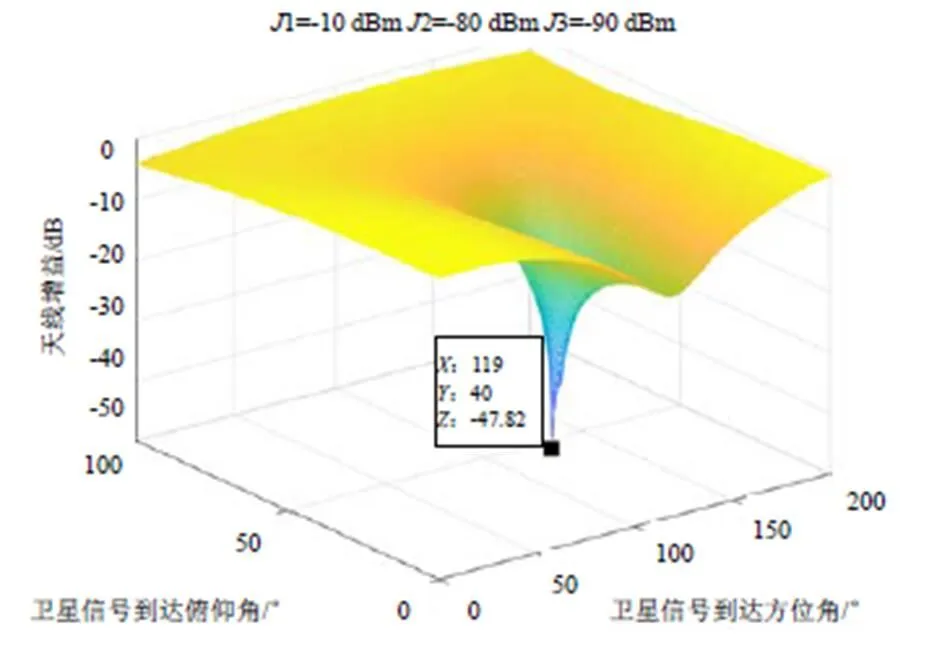
图5 两路多径信号入射下自适应调零天线方向图

4 结论

本文对暗室条件下多径对自适应调零天线影响进行了建模分析和仿真验证。当干扰及其多径进入到自适应调零天线时，理论上二者导向矢量等价成了一个导向矢量，该导向矢量既不指向干扰也不指向多径。该导向矢量虽不会额外增加方向图零陷点数目，但会造成零陷点从干扰位置拉偏，但随着干扰与多径信号强度差的拉大，多径的影响逐渐减弱。

[1] 吴仁彪，王文益，卢丹，等. 卫星导航自适应抗干扰技术[M]. 北京：科学出版社，2015.

[2] 田玉坤. 卫星导航自适应调零抗干扰算法研究与实现[D]. 西安：西安电子科技大学，2017.

[3] 赵飞，郎荣玲，李武涛. 基于子空间投影的功率倒置卫星导航抗干扰算法[J]. 现代导航，2017，10（5）：323-326.

[4] 樊昌信，张甫翊，徐炳祥，等. 通信原理[M]. 5版. 北京：国防工业出版社，2001.

[5] 马洪林. 卫星导航天线阵抗干扰测试场景设计技术研究[D]. 长沙：国防科技大学，2012.

[6] 李鹏程，冉一航，王淑君. 基于PI算法的自适应调零天线抗干扰技术研究[J]. 电子科技技术，2016，7（4）：471-474.

[7] 石荣，邓科，李渊，等. 两种功率倒置阵列天线调零模型的等效性分析[J]. 全球定位系统，2014，8（39）：4-7.

Analysis of Influence of Multipath Interference on Test of GNSS Array Anti-Jamming in Microwave Anechoic Chamber

WANG Leigang, QIAO Huidong, ZHOU Jihang, WANG Jianlu

When GNSS array anti-jamming performance is tested in microwave anechoic chamber, the power of multipath interference signal is still stronger than the navigation signal after absorption and attenuation. Whether the multipath affects the anti-jamming performance is an important factor of the test reliability. Based on the signal receiving model of antenna array, focusing on the covariance matrix of the received signal, the relationship between multipath signal and eigenvalue and eigenvector is analyzed in the paper. Then, based on power inverting model, the influence of multipath signal is simulated. The results show that when the strength difference between the interference and its multipath is less than a certain value, the null point of the array antenna will be pulled from the actual position; However, with the increase of the strength difference, the influence of multipath on the position of the null point decreases gradually.

Adaptive Nulling Antenna; Microwave Anechoic Chamber; Covariance Matrix; Multipath Effect

TN967.1

A

1674-7976-(2022)-01-001-06

2021-12-30。

王雷钢（1980.01—），河南禹州人，博士，助理研究员，主要研究方向为卫星导航及自适应导航接收机测试技术，协作导航定位技术等。