三维非齐次不可压缩Navier-Stokes-Vlasov方程组在移动区域上弱解的整体存在性
张师豪,王丽真
(1.西北大学 非线性科学研究中心,陕西 西安 710127;2.西北大学 数学学院,陕西 西安 710127)
在物理学中,喷雾指的是一种悬浮在气体(如空气)中的微小粒子的混合物,可以由流体和粒子通过摩擦力耦合得到的模型来描述。近年来,流体-粒子耦合模型已被广泛研究,并被应用于各个方面,如大气污染、沉降问题[1-2]、汽油发动机和柴油发动机中的燃料喷射器、火箭发动机的喷射器等工业原件[3-4]。本文考虑了三维非齐次不可压缩Navier-Stokes-Vlasov方程组在移动区域Ωt上弱解的整体存在性,方程组形式如下
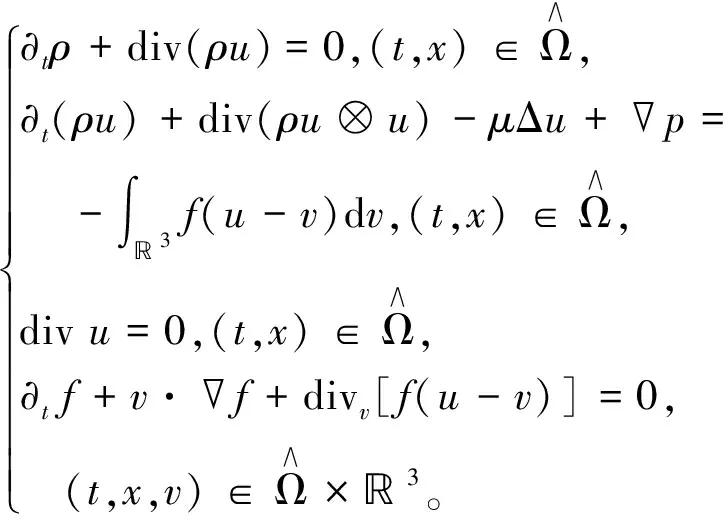
(1)
其中ρ(t,x)∈,u(t,x)∈3,p(t,x)∈分别为流体密度、速度以及压力,f(t,x,v)∈为粒子的密度分布函数,μ>0为流体的黏性系数。
考虑如下的初边值条件,其中初始条件为

(2)
边界条件为

(3)
在本文,设T>0为有限常数,B为3中的开球,Ω⊂3为有界开集且为∂Ω的单位外法向量,c1为正常数。此外,定义映射A∈C2(+×3;3),即
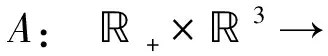
使得∀t∈[0,T],At是一个C1-微分同胚,在Bc中At=id。且在3中当t=0时,A0=id(id为3上的恒等映射)。定义欧拉速度ω满足
∂tA(t,y)=ω(t,At(y)),(t,y)∈[0,T]×3。
由上述At的假设知,
ω(t,x)≡0,(t,x)∈(0,T)×Bc。

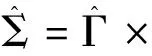
ηt(x)>0},
ηt(x)=0},

ηt(x)>0},∀t∈[0,T]。
近年来,流体-粒子耦合模型解的适定性研究被广泛关注,许多学者研究了该模型解的存在性并得到了一系列经典的结论。对于不可压缩的情形,最早的结果是Hamdache[5]考虑了在有界区域中Vlasov-Stokes方程组弱解的整体存在性和大时间行为。其次,Boudin等[6]证明了三维周期区域中不可压缩Navier-Stokes-Vlasov方程组弱解的整体存在性,他们将其结果在文献[7]中推广到了移动区域。Yu[8]证明了二维和三维有界区域中弱解的整体存在性。接着,Wang等[9]将其结果推广到了非齐次不可压缩Navier-Stokes-Vlasov方程组情形。接下来,Chen等[10]基于能量估计和弱收敛方法证明了非齐次不可压缩MHD与Vlasov方程耦合模型弱解的整体存在性。对于可压缩情形的结果相对较少,Mellet等[11]证明了可压缩Navier-Stokes-Vlasov-Fokker-Planck方程组弱解的整体存在性,并基于相对熵方法在文献[12]中得到了该方程组的流体动力学极限。对于其他相关模型解的存在性,Baranger等[3]证明了可压缩Euler-Vlasov方程组经典解的局部存在性。其次,Mathiaud[14]证明了Euler-Vlasov-Boltzmann方程组经典解的局部存在性。然而,到目前为止,三维非齐次不可压缩Navier-Stokes-Vlasov方程组在移动区域中弱解的整体存在性还未解决。本文基于文献[7]的想法,假设流体的初始密度有下界,得到了三维非齐次不可压缩Navier-Stokes-Vlasov方程组在移动区域中弱解的整体存在性。
本文证明的是三维非齐次不可压缩Navier-Stokes-Vlasov方程组在移动区域上弱解的整体存在性。与文献[7]相比,在证明过程中会遇到一些困难。首先,考虑初边值问题(1)~(3)时需处理密度函数ρ(t,x)和分布函数f(t,x,v)的存在唯一性。其次,利用弱收敛方法,在逼近方程组(12)中关于n取极限的过程中,由于无法得到估计

1 主要结论及逼近系统的构造
首先规定
1.1 能量不等式

(4)
对式(1)第2式两边同乘以(u-ω)并在Ωt上积分,并利用式(4)得
(5)

(6)
将式(5)与式(6)相加,可得
(7)
结合边界条件式(3)第2式知,
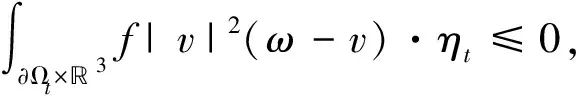
(8)
再利用
代入式(7)可得,
(9)
其中,
对式(9)两边关于时间在(0,t)上积分得
Eρ,u,f(0)。
(10)
此外,对式(1)第1式在Ωt上积分,并利用式(4)得
对式(1)第4式在Ωt×3上积分,并利用式(4)和式(8)得
从而式(10)可以进一步改写为如下形式,
(11)
利用Grönwall不等式,得
[CEρ,u, f(0)+C(ω,ρ0,f0,μ)T]eC(ω,ρ0,f0,μ)T。
为定义三维非齐次不可压缩Navier-Stokes-Vlasov方程组的初边值问题(1)~(3)的弱解,引入以下空间[7]:
监管部门应针对法律法规,制定出一套以碳会计信息披露系统为基础的监管体系,及时监督企业的碳会计信息披露情况。对碳信息披露不及时或消极披露碳信息的企业,要制定一套奖惩体系,明确责任,加大对碳会计信息的重视,将企业碳会计信息披露与信誉关联,对企业未来的经营形成一定影响。
L2(0,T;H1(Ωt))=
V={ψ∈L2(0,T;H1(Ωt))|divψ=0},
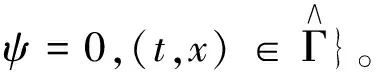

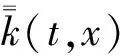

此外对任意p∈[1,∞),有
L∞(0,T;Lp(Ωt×3))={f为可测函数3×3))},

1.2 主要结论及预备知识
在给出主要结论之前,首先定义三维非齐次不可压缩Navier-Stokes-Vlasov方程组的初边值问题(1)~(3)的弱解。
定义1称(ρ,u,f)为三维非齐次不可压缩Navier-Stokes-Vlasov方程组的初边值问题(1)~(3)的弱解,如果下列条件成立:

iii)u-ω∈V0;


vii) ∀ψ∈V且对几乎处处的t∈[0,T],
viii) ∀φ∈W,∀t∈[0,T],
定理1三维非齐次不可压缩Navier-Stokes-
Vlasov方程组的初边值问题(1)~(3)在定义1的意义下至少存在一个弱解(ρ,u,f)。
为了证明定理1,下面将陈述本文中所需的主要引理。

引理2[7](Schaefer不动点定理)
设E为一个Banach空间,θ:E×[0,1]→E是一个连续映射,且将E×[0,1]中的有界集映为E中的相对紧集。记θσ=θ(·,σ),如果θ0=0以及集合{u|θσ(u)=u,σ∈[0,1]}在E中有界,则θ1在E中至少有一个不动点。
1.3 构造逼近系统
下面构造问题(1)~(3)的逼近系统,具体步骤如下:
第1步 将方程组(1)第2式中的对流项正则化,为保证逼近系统的能量估计,同时将方程组(1)第1式中对应的u正则化;
第3步 由于摩擦力项f(u-v)控制系统的耦合项,为了利用文献[17-18]中关于非齐次不可压缩Navier-Stokes方程组的标准存在性和正则性结果,这里需截断方程组(1)第2式等式右边的耦合项。此外,为了保持逼近系统的能量估计,在方程组(1)第4式中也做相同的截断。为此,引入一个递增且有界的奇函数χ∈C∞()满足∀z∈[0,∞),0≤χ(z)≤z。并且当z∈3时,χ(z)=(χ(z1),χ(z2),χ(z3))。
构造问题(1)~(3)的逼近系统如下:
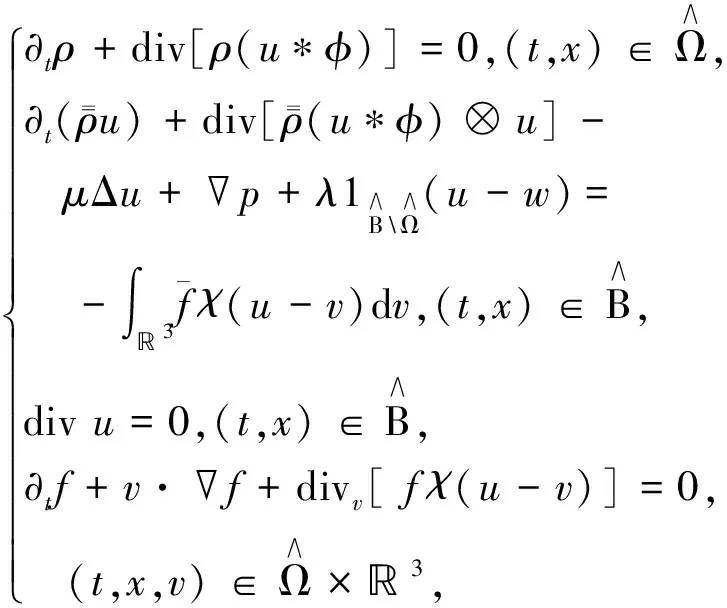
(12)


(13)
2 逼近系统解的存在性
本节将利用引理2证明逼近系统(12)~(13)弱解的存在性。

(14)
其中u0满足逼近系统(12)~(13)所定义的初值条件。故Schaefer不动点定理中映射θ可以定义为
2.1 ρu和fu的存在唯一性
2.1.1fu的存在唯一性fu的存在唯一性已由文献[7]给出证明,为了文章结构完整,现陈述如下:
考虑Vlasov方程初边值问题

(15)
其中,函数G(t,x,v),f0(x,v)给定。首先给出Vlasov方程初边值问题(15)的弱解定义。
定义2[7]若对任意测试函数φ∈W,且φ(T,·)=0有

引理3[7](fu的存在性定理)

exp(T‖divvG‖L∞(0,T;L∞(B×3)))
‖f0‖L1(Ω×3)∩L∞(Ω×3)。
引理4[7](迹定理)
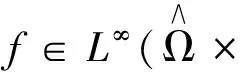
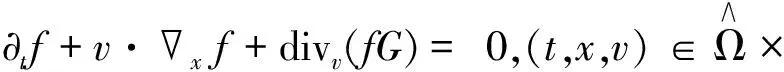
(16)
引理5[7](fu的唯一性定理)
令f∈L∞(0,T;L1(3×3))∩L∞(0,T;L∞(3×3))为Vlasov方程初边值问题(15)在定义2下的弱解,并且3))+L1(0,T;L∞(B×3)),则f≡0。
现令上述引理中G(t,x,v)=χ(u-v),可得Vlasov方程初边值问题(15)有唯一弱解fu。
2.1.2ρu的存在唯一性
考虑下述问题

(17)


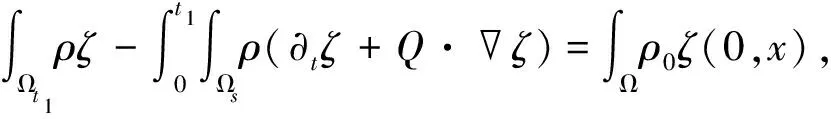
(18)

下面考虑Q(t,x)∈D(×3), 且对任意
s∈,x∈3,下述微分系统
ρ(t,x)=ρ0(xs(0))。

ρ(t,x)≥c1,
因此得到下述命题:

ρ(t,x)≥c1,
下面考虑问题(17)弱解ρu的唯一性。假设ρ1,ρ2都为问题(17)在定义3的弱解,且
接下来只需证明ρ≡0,即可说明问题(17)弱解的唯一性。

证明由于ρ为问题(17)在定义3下的弱解,取非负函数φ(x)∈D(3)使得

从而,
故

2.2 逼近系统解的存在性
要证明逼近系统(12)~(13)解的存在性,需证明Schaefer不动点定理所满足的条件:
i) 映射θ的良定性;
ii) 映射θ:E×[0,1]→E的连续性和紧性;
iii) 集合{u|θσ(u)=u,σ∈[0,1]}在E中的有界性。
若以上条件成立,则θ1至少存在一个不动点,即可证明逼近系统(12)~(13)解的存在性。
首先,证明映射θ的良定性。

现已将式(14)第1式中的对流项正则化,利用文献[17-18]中非齐次不可压缩Navier-Stokes方程组的标准存在性和正则性理论,只需证明
L2((0,T)×B),
由于
|λ|(‖u‖L2((0,T)×B)+‖ω‖L2((0,T)×B)),

其次,证明映射θ:E×[0,1]→E的连续性和紧性。
考虑序列(un,σn)∈E×[0,1],且当n→∞时,(un,σn)→(u,σ)。对∀n∈*,令要证θ的连续性,即证在空间E中
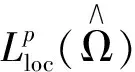



H1(0,T;L2(B))∩L2(0,T;H2(B))∩


由文献[17-18]中非齐次不可压缩Navier-Stokes方程组的标准存在性和正则性理论知,

‖f0‖L1(Ω×3)∩L∞(Ω×3)),
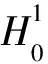
最后,证明集合{u|θσ(u)=u,σ∈[0,1]}在E中的有界性。
(19)
在式(16)中取t0=0,t1=t,G=χ(u-v),β(z)=z,ψ=|v|2,得
(20)


(21)
将式(21)乘以σ,再加上式(19)得
(22)

(23)
由Grönwall不等式,
故{u|θσ(u)=u,σ∈[0,1]}在E中有界。此时,由Schaefer不动点定理,逼近系统(12)~(13)弱解的存在性得证。
3 定理1的证明
在第2节中已证明逼近系统(12)~(13)弱解的存在性。故对任意n∈*,(ρn,un,fn)是下述逼近系统的解

(24)
其中{φn}为磨光序列,截断函数列{χn}是一个递增的有界奇函数列,且满足对∀n∈*,
{χn}⊂C∞(),
此外,系统(24)补充定义了以下初值条件:
(ρn(t,x),un(t,x),fn(t,x,v))|t=0=


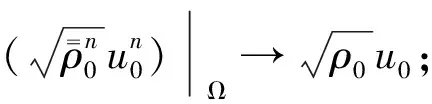
在Lp(Ω×3)(1≤p<∞)中,
在L∞(Ω×3)中,


对于上面的逼近系统(24),需要得到一个类似于式(23)的估计,但这个估计不能依赖于正整数n。类似于式(22),可得
(25)


(26)
从而,
(27)
将式(25)与式(27)相加,结合|χn(z)|2≤
χn(z)·z得

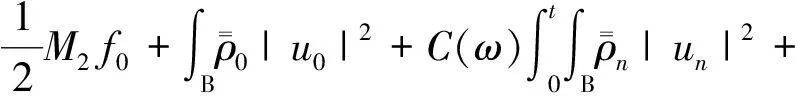
(28)
由Grönwall不等式得
(29)
且当n→∞时
故

在L∞(0,T;L∞(3×3))中,
在L2(0,T;L2(B))中,un⇀u,un⇀u;
在L∞(0,T;L∞(3×3))中,



其中,
φn‖L6(B)‖ψ‖L3(B)≤
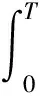
C‖ψ‖L3(0,T;W1,3(B))。
利用fn(t,x,v)关于v具有紧支集知,
C‖ψ‖L3(0,T;W1,3(B))。
从而,
利用文献[15]中定理2.4知,

在Lθ(0,T;L3θ(B))中,un→u,


由式(29)和引理1知,
可得,
其中常数C与n无关。故
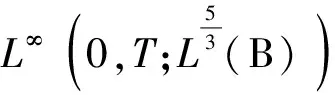



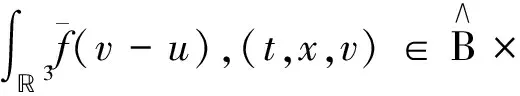
从而在分布的意义下,有
div[(ρn(un*φn)⊗un)]→


故三维非齐次不可压缩Navier-Stokes-Vlasov方程组在移动区域上弱解的整体存在性得证。

