利用首次积分法求解一致时空分数阶微分方程
王丽真,沈 翔
(1.西北大学 非线性科学研究中心,陕西 西安 710127; 2.西北大学 数学学院,陕西 西安 710127)
随着科学技术的深入发展,在热学、流变学、材料和力学系统、信号处理、系统识别、控制科学、生物科学、工程学、气象学等诸多领域中,整数阶微分方程已经不能满足人们的研究需求,进而分数阶微分方程被越来越多的研究者采用。早在300多年前,洛必达就提出了这样的问题:什么是二分之一阶导数?这个问题被后来的诸多科学家们不断研究,发展出了诸多分数阶导数的定义,常见的如Riemann-Liouville型分数阶导数、Caputo型分数阶导数,其中,Caputo型分数阶导数在物理领域应用更广泛[1]。但是,前人所定义的微分算子亦有其缺陷,即不满足整数阶导数所具备的一些运算性质。2014年,Khalil及其合作者发现了新的分数阶导数的定义,即一致分数阶导数,它具有许多经典微积分的性质,如半群性质、复合函数的链式法则[2]。2015年,Abdeljawad等人研究了一致分数阶微分算子的半群性质[3]。2015年,Çenesiz等人研究了基于一致傅里叶变换下的一致分数阶时空热方程的解[4]。2016年,Benkhettou等人研究了任意时间尺度上的一致分数阶微积分问题[5]。2016年,Mehmet等人研究了一致分数阶积分的Grönwall型不等式[6]。2017年,Ünal等人采用微分变换法研究了一致分数阶常微分方程的解[7]。2017年,Lazo等人研究了一致分数阶导数的变分法[8]。2018年,Thabet等人通过分数阶微分变换建立了一致时空分数阶偏微分方程的解析解[9]。2019年,李倩倩研究了一类一致分数阶微分方程解的稳定性[10]。2021年,闫立梅等人利用不变子空间方法求解了一致分数阶导数模型[11]。
本文介绍了一致分数阶微分算子及首次积分法;采用首次积分的方法求解了一类一致分数阶时空偏微分方程——修正的Benjamin-Bona-Mahoney方程(简称m-BBM方程);最后,借助Maple软件,给出了不同参数下解的图像。
1 一致分数阶微分算子及其性质
定义1给定一个函数f:[0,+∞)→。则f的α阶一致分数阶导数定义为
定理1若α∈(0,1],且f,g在点t是α阶可导的,则有
1)Dα(af+bg)=aDαf+bDαg,∀a,b∈,Dα(tm)=mtm-α,∀m∈,
2)Dα(f·g)=gDαf+fDαg,
5)Dαk=0,k∈。
2 首次积分法
冯兆生在2002年通过Hilbert-Nullstellensatz定理得到了双变量的除法定理,从而通过除法定理寻找方程的首次积分[12]。
假设存在一个关于独立变量x,y,t的一致分数阶非线性偏微分方程
Dαux,Dαuy,uxxx,…)=0,0<α<1。
(1)
首先,做变换

(2)
利用定理1,如下结论成立:
将上述结论代入式(1)中,从而得到一个新的非线性常微分方程:
G(u,u′,u″,u‴,…)=0 ,
(3)
其次,定义
X(ξ)=u(ξ),Y(ξ)=u′(ξ) 。
(4)
由式(3)、(4)引出一个非线性常微分方程组
由常微分方程定性理论,如果相同的条件下能找到该方程组的积分,那么它的一般解可以直接得到。
定理2(除法定理)假设P(x,y)和Q(x,y)是C[x,y]关于x和y的两个二元多项式,且P(x,y)在C[x,y]上是不可约的。若Q(x,y)在P(x,y)=0的点都为0,则存在一个C[x,y]中的多项式G(x,y),使得
Q(x,y)=P(x,y)G(x,y)。
3 Riccati方程及其精确解
利用首次积分法,通常会将方程化为一种特殊的常微分方程——Riccati方程。文献[13]介绍了如下Riccati方程:
U′=r+pU(ξ)+qU2,r,p,q∈,q≠0。
并给出了当Δ=p2-4rq<0时,方程的如下精确解:
其中A,B是非零实数,且满足B2-A2<0。
其中广义的三角函数定义如下:
4 利用首次积分法解一致时空分数阶m-BBM方程

为此考虑如下的一致时空分数阶m-BBM方程
η>0,μ≠0。
(5)
做变换
(6)
对式(6)应用定理1,则有

(7)
故原方程式(5)化为
-ωU′(ξ)-ληU2U′(ξ)+λ2ωμU‴(ξ)=0,
(8)
对式(8)两边同时积分,并取积分常数为0,得
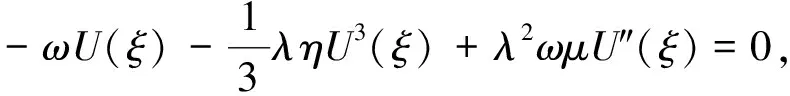
(9)
将式(9)化为

(10)
方便起见,记

(11)
故式(10)可化为
U″=MU+NU3,
(12)
由式(6),令
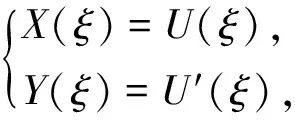
(13)
结合式(12)、(13),得到方程组

(14)
设X,Y是方程组(14)的非平凡解,并且存在不可约多项式
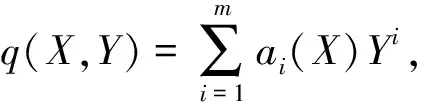
(15)
使得
q(X,Y)=0,
(16)
其中ai(X)(i=0,1,…,m)是关于X的多项式,并且am≠0。由定理2,存在多项式g(X)+h(X)Y使得
(17)
设m=1,则可由式(17),得
a0(X)g(X)+a1(X)g(X)Y+
a0(X)h(X)Y+a1(X)h(X)Y2=
a1(X)·[MX+NX3],
对比Yi(i=0,1,2)的系数,得到
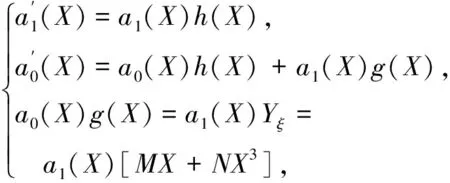
(18)
(19)
对比系数,并由式(11),解得

(20)
代入式(15)、(16),得
(21)
再由式(15)、(16),可知
(22)
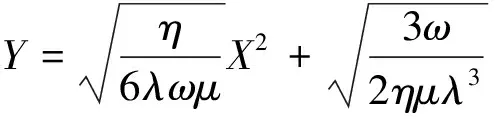

其中,A,B是非零实数,且满足B2-A2<0。
5 利用Maple软件画出精确解图像
使用Maple软件分别画出了所得部分精确解的图像,并对比了同一解取不同阶数时的行为和解的分布情况(见图1~6)。

注:λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.001,ξ0=0,μ=3,η=4图1 U5 的三维图和密度图(β=0.001)Fig.1 3-dimensionalFigure and densityFigure of U5(β=0.001)

注:λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.999,ξ0=0,μ=3,η=4图2 U5的三维图和密度图(β=0.999)Fig.2 3-dimensionalFigure and densityFigure of U5(β=0.999)
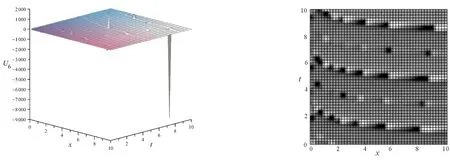
注: 取正号图3 U6的三维图和密度图(β=0.001)Fig.3 3-dimensionalFigure and densityFigure of U6(β=0.001)
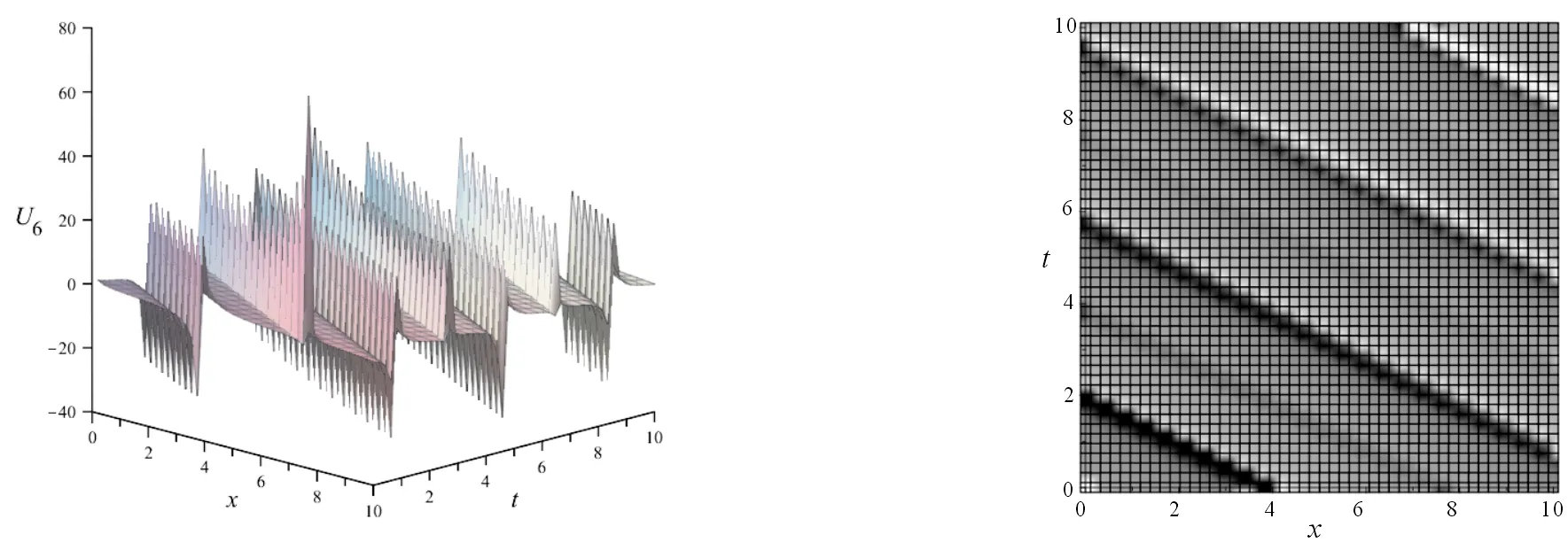
注: 取正号图4 U6的三维图和密度图(β=0.999)Fig.4 3-dimensionalFigure and densityFigure of U6(β=0.999)

注:λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.001,ξ0=0,μ=3,η=4图5 U9的三维图和密度图(β=0.001)Fig.5 3-dimensionalFigure and densityFigure of U9(β=0.001)

注:λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.999,ξ0=0,μ=3,η=4图6 U9的三维图和密度图(β=0.999)Fig.6 3-dimensionalFigure and densityFigure of U9(β=0.999)
通过对比U5、U6、U9的三维图和密度图可知,参数β对解的图像影响较大。在保持其他条件不变,取β=0.001时,其解整体振幅较小,但是在个别点的振幅非常大;而取β=0.999时,其振幅始终在一个相对较小的范围内。
6 结语
本文主要通过首次积分的方法,构造了一致时空分数阶m-BBM方程的精确解。先将偏微分方程化为常微分方程组;再利用除法定理求出解析解;最后,结合Riccati方程的已知解得到所求方程的精确解。研究表明,首次积分方法对于求解时空分数阶偏微分方程而言是一种简洁有效的方法。

