引入换手率相关指标的多因子模型——A股实证分析

李羊骥

(江苏师范大学科文学院， 江苏徐州 221000)

一、引言

作为新兴资本市场，中国A股市场的投资者在信息渠道、交易理念等方面都与西方发达国家成熟股市的投资者有较大的差异。我国的股市散户交易量庞大，信息不对称现象显著，散户交易追涨杀跌的羊群效应在极大程度上影响了市场定价。在基本面学派进行了大量的因子研究之后，诸如规模、盈利、财务状况、管理者能力、分红派息等各类因子已经被证明在A股市场有一定的解释力度，但是模型依然存在无法解释的市场异象。甚至某些在美股被证明有效的基本面因子，用A股数据进行验证之后发现因子收益率并不显著，或者收益率与基本面理论相悖。这些看似违背了金融学或会计学理论的研究结论，正是因为A股这种特殊的市场有其自己的定价特点。投资者本身的异常行为干涉了因子的正常定价，A股也缺乏有效的做空机制(融券的券源是很有限的，且成本太高)，而散户与机构投资者互相的博弈增加了特质波动率，最终使得传统多因子模型的回归结果不显著，出现了无法解释的异象。

为了探究除基本面因子之外的有效因子，本文从股票的换手率出发，分别构造传统的换手率因子和异常换手率因子尝试对A股进行定价，从历史回测的角度分析因子收益率的稳健性。最终发现，换手率因子和异常换手率因子都具有显著的解释力度，因子收益率显著，基于这两类因子构造的投资组合可以获取稳健的超额收益。

二、文献综述

20世纪30年代的Graham and Dodd在Security Analysis一书中提出了价值溢价的概念，被价值投资流派奉为经典[1]10-13。随后70年代的CAPM和APT模型的问世，第一次为资产定价领域带来定量分析模型。

虽然CAPM能够在一定程度上解释资产的超额收益，但是学术界的研究发现CAPM无法解释普遍存在的资产收益异象。1973年Fama和Macbeth提出了Fama-Macbeth回归方法，用以检验CAPM的有效性。该方法有效地规避了收益率随机扰动项的截面相关性的影响[2]。1993年Fama和French的三因子模型横空出世，该模型在CAPM的市场因子基础上，加入了代表便宜股效应的HML因子和代表小市值效应的SMB因子。该模型奠定了现代实证资产定价领域的基础,文章中首创的利用独立双重排序的方法排除单因子在其他因子上的暴露的做法，也为后世的学者提供了统一的分析方法，后续的多因子模型多数都会跟该模型做对比。随后二位学者又在2015年加入了投资因子和盈利因子，提出解释力度更强的Fama-French五因子模型。Carhart利用股票t-12到t-1个月之间的累计涨跌幅作为动量因子，剔除了最近一个月的反转效应，首次提出包含动量的四因子模型，证明了动量因子在美股市场的有效性[3]。Novy-Marx使用毛利率代替净利率作为盈利因子，该文认为毛利率受到的操纵性较低，而传统的ROA或ROE指标中的净利润容易受到上市公司的操纵，并且对因子进行了行业中性化处理，增强因子的可比性[4]。近年来，行为金融学领域的学者也开始进行多因子模型研究。Shefrin和Statman从认知偏差的角度区分噪声交易者和信息交易者，分析了噪声交易者的交易行为对股票价格、波动率、成交量的影响，最终发现噪声交易者的行为会弱化资产收益率与贝塔值之间的关系，对资产收益率产生影响[5]。Brown和Cliff指出尽管投资者情绪的波动与当期市场波动有较强的相关性，但情绪的波动对下一期的市场走势判断没有显著的预测能力[6]。Stambaugh和Yuan利用Fama-French三因子模型无法解释的11种异象够早了管理因子和表现因子，提出了行为金融学领域的多因子模型。该模型创造性的用行为金融学的指标作为定价因子[7]。

在中国的A股市场上，也有许多学者发现了有效的多因子模型。吴世农和许年行、潘莉和徐建国等国内学者将Fama-French三因子模型用于A股市场进行实证分析，得出三因子模型比CAPM更能解释A股超额收益的结论[8]。王美今和孙建军从理论上证明了投资者情绪会影响资产的均衡价格，利用A股数据进行实证分析，发现投资者情绪对市场收益有显著影响。伍燕然等从投资者情绪的角度，利用中国的封闭式基金数据进行实证研究，结果表明投资者情绪对市场短期收益有正向影响，而对市场长期收益有反向影响[9]。陈其安等建立了资产定价模型，分析了噪声交易者对股票市场价格与波动率的影响机理，进而认为中国股票市场中的异象在很大程度上是由噪声交易者造成的。Liu等人提出A股市场三因子模型，该文章针对A股借壳上市的“壳污染”问题，剔除了A股上市公司市值最小的30%的公司，并使用EP指标代替BM作为价值因子，使三因子模型的结论更可靠[10]。赵胜民等从行为金融领域的前景理论出发，将投资者偏好以定价因子的形式引入多因子模型，最终发现股票的前景理论价值与预期收益率之间存在显著的负相关关系[11]。

早期的学者普遍将换手率作为股票流动性的衡量指标，换手率的定义是一定时间窗口内的成交额除以股票的流通市值。早在20世纪20年代，著名交易员Jessie Livermore就曾在自己的回忆录中披露了成交量放大与趋势形成之间的关系[12]103-110。Barinov认为换手率与市场的总体波动率相关，他指出换手率异象在那些有期权形态的股权结构中最为显著[13]。Chen等人认为换手率因子与股价崩盘风险相关，发现换手率相对于过去6个月的趋势显著增长且在过去36个月内显著正收益的股票有着最高的崩盘风险[14]。Odean和Statman等指出换手率反映了投资者非理性的情绪，例如过度自信和盲目乐观，可以作为一种情绪代理指标[15]。Lee和Swaminathan认为换手率和投资者关注度以及投资者分歧显著相关。Chou等人发现换手率与股票预期收益率的负相关性无法被Fama和French三因子模型和CAPM解释[16]。此外，他们还发现换手率异象的高度持续，在之后的五年之内都可以获取显著的超额收益。

除了传统的换手率研究之外，不少学者针对异常换手率做了研究。

从行为金融学的角度来说，A股市场的散户交易量庞大，羊群效应、信息不对称等因素使得市场的有效性弱于欧美股市，在A股市场运用技术指标具备获取Alpha收益的基本条件。换手率是衡量股票流动性、交易热度的指标，高换手率的股票一般代表散户正在追涨杀跌，而低换手率的股票则代表还没有被炒作，未来有一定上涨空间。

现存的多因子研究主要集中于因子是否具备在统计学意义上的显著性。但是实证资产定价的最终目的还是应当回归到现实中，力求寻找出在二级市场上可以帮助投资者获取稳健超额收益的因子。本文的分析框架中除了传统的回归模型分析之外，还加入了历史回测部分，用以验证模型研究的结论在投资实战中的作用。

三、数据处理与因子构建

1.模型搭建

资产定价领域使用的计量方法主要有时间序列回归、横截面回归和Fama-Macbeth回归方法。本文选择的计量建模方法是Fama-Macbeth线性回归，该方法优点在于它规避了回归残差的截面相关性的影响，在学术界广泛用于因子的有效性检验。Fama-Macbeth回归方程如下：

Ri, t+1=β0, t+β1, t*Marketi, t+β2, t*Sizei, t+β3, t*BMi, t+β4, t*ROEi,t+β5, t*TORi,t+ei, t+1

其中：

Ri, t+1：股票i在t+1时刻的收益率，本文采用的是股票月度收益率。

β0, t：回归模型的截距项。

β1, t,β2, t,β3, t,β4, t,β5, t：因子的回归系数。

ei, t+1：回归模型的残差

Marketi, t：股票i在t时刻的市场因子，用252个交易日滚动窗口序列对大盘指数做回归得到的beta值作为市场因子。

Sizei, t：股票i在t时刻的规模因子，用股票流通市值的自然对数作为规模因子。

BMi, t：股票i在t时刻的价值因子，用BM指标即公司的账面价值除以市值作为价值因子。

ROEi, t：股票i在t时刻的盈利因子，采用净资产收益率ROE作为盈利因子。

TORi,t：股票i在t时刻的换手率/异常换手率因子，换手率因子计算方法详见下面的因子构建部分。

2.因子构建

本文的所有原始数据均来自国泰安数据库(CSMAR)，包括2000年1月至2020年12月的全部A股股票(剔除科创板)的月度K线数据、市值数据，以及季度、半年度以及年度财务报表数据。在剔除异常数据和滚动计算的缺失值之后，有效数据窗口为2000年6月至2020年11月。参考学术界的最新做法，用公司特征值亦即指标本身的数值作为因子暴露。

各因子暴露的计算方法如下：

(1)市场因子。使用252个交易日的滚动时间窗口序列，使用上证指数与深证成指对个股进行线性回归，得出个股的市场因子(beta值)。

(2)规模因子。对股票当月月末流通市值取自然对数，去除异常值。

(3)价值因子。用公司的归属于母公司所有者权益合计，除以月末的总市值，去除异常值。

(4)盈利因子。根据国泰安数据库中的归属于母公司净利润的季度数据，计算最近连续4个季度的归母净利润(TTM)。再用该数据除以月末的归属于母公司所有者权益合计，得出最终的ROE，去除异常值。

(5)换手率因子。用个股月度成交额除以月末流通市值得到换手率因子，用20日移动平均换手率除以252日移动平均换手率的比率，作为异常换手率因子。

使用公司特征值直接作为因子暴露是学术界的近期的流行做法。与常规的时间序列回归方法相比，公司特征值可以更直接地体现出股票在各个单因子上的暴露，且不会受到其他因子的影响。

四、模型结果

本文的回归建模所用到的数据为2000年6月至2020年11月，当月的五个因子暴露作为自变量，在t月用t+1月的个股超额收益率作为因变量，进行横截面回归，因此会有232次横截面回归。回归之后可以得到每个因子收益率的时间序列，在此基础上进行假设检验。

在学术界的研究框架中，学者习惯于将因子暴露先进行标准化处理，之后再做回归，便于分析不同因子对股票超额收益率的影响。本文为了尽量保证因子暴露的纯粹性，借鉴了石川的《因子投资》与Turan Ball、Robert Engle和Scott Murray的《实证资产定价》的做法，使用公司特征值(即因子指标)作为因子暴露，直接对未经标准化的因子暴露做回归。

为了让回归结果中不同因子的收益率具有可比性，将因子的月均收益率(即回归系数均值)乘以因子暴露的横截面标准差，得到影响系数。如影响系数为1%，意味着其他条件不变时，目标因子1个标准差的波动会带来股票超额收益率1%的波动。

加入传统换手率因子的五因子模型回归结果如表1：

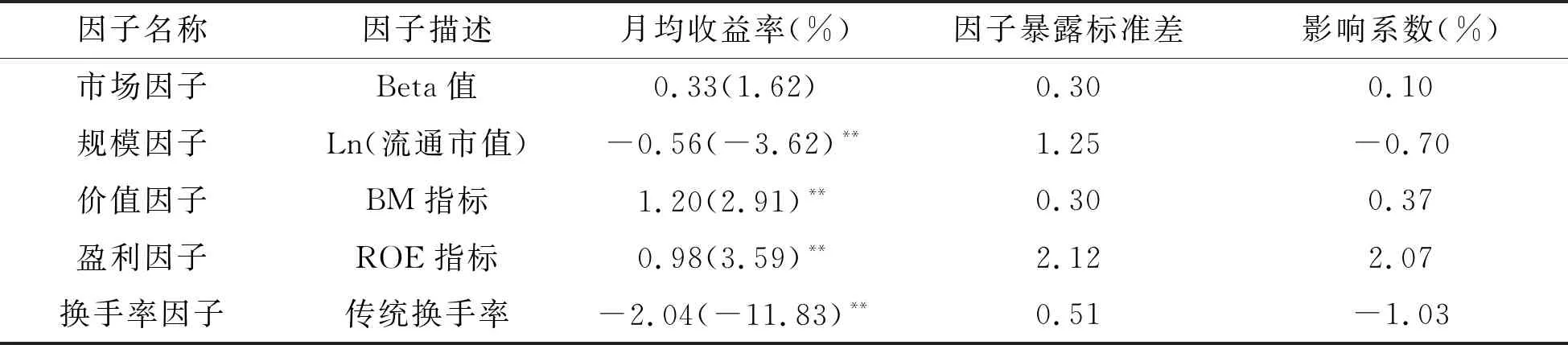
表1 五因子回归模型结果—传统换手率

表1显示，市场因子的收益率无法通过Newey-West调整后的t检验，其收益率与影响系数均很小。规模因子的收益率显著为负，价值因子和盈利因子收益率显著为正，这与传统的Fama-French三因子模型是一致的。换手率因子的收益率显著为负，-1.03%的影响系数表示换手率1个标准差的变化会带来股票超额收益率1.03%的反向变化。换手率因子收益率经过Newey-West调整之后的t值为-11.83，通过了5%显著性水平的t检验，可以看出换手率与股票超额收益率有显著的负相关关系。

从表2中可以清楚地看到，市场因子的收益率依然无法通过Newey-West调整后的t检验，而且这次变成了负数，与CAPM不符，但符合Black CAPM的结论。规模因子的收益率依然显著为负，价值因子和盈利因子收益率显著为正。异常换手率因子的收益率显著为负，-0.70%的影响系数表示换手率1个标准差的变化会带来股票超额收益率0.70%的反向变化。异常换手率因子收益率经过Newey-West调整之后的t值为-8.68，通过了5%显著性水平的t检验，可见异常换手率与股票超额收益率有显著的负相关关系。

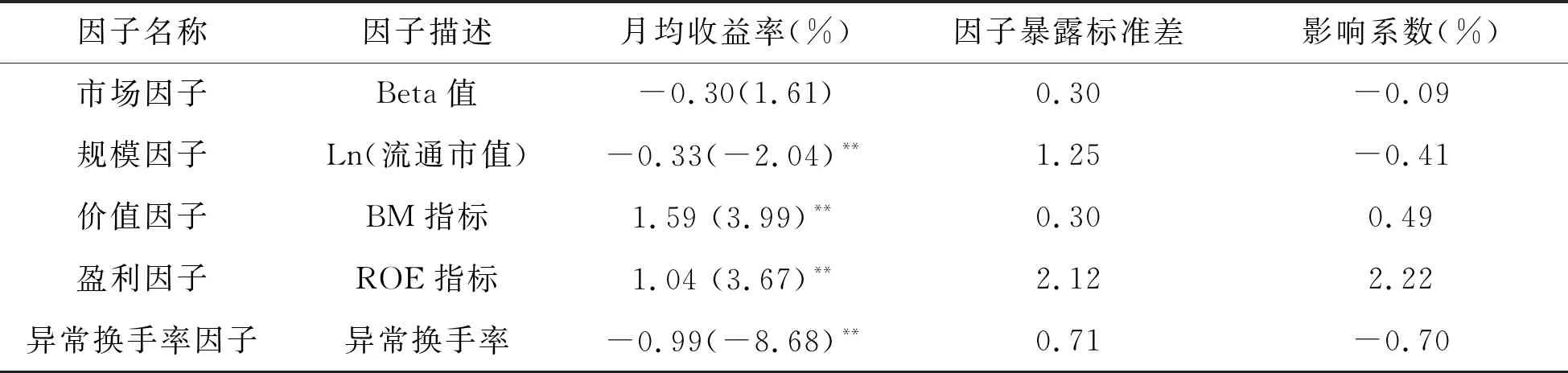
表2 五因子回归模型结果—异常换手率

五、历史回测分析

1.Rank IC、IR指标分析

量化投资业界挑选有效因子的时候比较注重的指标是IC和IR。IC的全称是Information Coefficient，即信息系数。其定义是t+1时刻的预测收益率与t时刻的指标值(例如代表规模因子的流通市值的自然对数)的相关系数。实际应用中更常用的是Rank IC，其定义是t+1时刻的收益率横截面排名与t时刻的指标值的横截面排名的相关系数，公式如下：

Rank IC =corr[Rank(Returni, t+1), Rank(factori, t)]

其中，Rank(Returni, t+1))表示股票月度收益率在t+1时刻的排名，Rank(factori, t)表示因子暴露在t时刻的排名。

IR全称为Information Ratio，即信息比率，是衡量IC稳定性的指标。其定义是IC序列的均值除以标准差。按照上述计算方法，包含传统换手率因子的五因子模型的Rank IC和IR值见表3：

表3 因子的Rank IC 和 IR值

根据业界传统，Rank IC均值的绝对值在2%以上，可以初步判定该因子是比较有效的。按照这个阈值来判断，市场因子的Rank IC无法通过检测，而换手率因子的Rank IC是最显著的，且IR的绝对值达到0.52。异常换手率的Rank IC也很高，且其IR是因子里面最高的，可以初步判断两种换手率因子的预测稳定性较强。

2.因子选股收益回测

在用Fama-Macbeth回归方法以及Rank IC和IR指标验证了换手率因子的有效性之后，还需要进行最后一个检验，即历史数据回测。通过历史回测可以清晰地看到换手率因子的选股收益情况，并且可以对收益的稳定性、最大回撤等指标做进一步分析。

根据A股市场的交易制度，回测时设定交易手续费为万分之1.5，印花税为千分之1。每个月末进行动调仓，等权重分配资金，结果如下：

从历史回测结果来看，换手率和异常换手率因子都可以获取显著的超额收益。选择换手率最低的前20%的股票，2000年6月至2020年12月可以获取9.68倍的资金曲线。选择异常换手率最低的前20%的股票可以获取11.33倍的资金曲线(见图1、图2)。

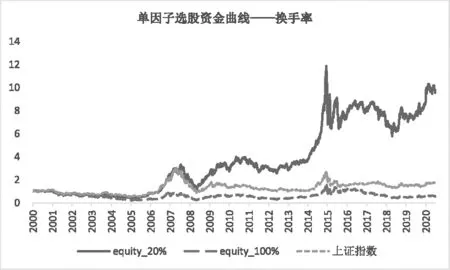
图1 换手率因子选股回测结果

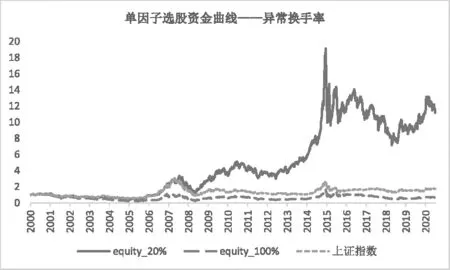
图2 异常换手率因子选股回测结果

表4列出两种单因子选股年化收益的单调性统计表，表格中的第一行数字为年化收益，括号中的数字为历史最大回撤：

表4 单因子选股收益率统计表

从表4中可以看出，换手率因子的收益除了第二组之外，大致符合单调性的要求，即随着换手率的提升，单因子选股收益率在降低。异常换手率因子五个组都符合单调性要求，两种因子选股的历史最大回撤比较接近。

尽管换手率和异常换手率均可以获取显著的超额收益，但是也应当注意到，A股的许多因子之所以有效，很大程度上是因为具有规模因子暴露。要想验证因子本身的有效性，还应当对因子的相关性进行考察，从换手率因子中将规模因子的暴露剥离出去再做回测(见表5)。

表5 因子暴露相关系数矩阵表

从上表5中可以看出，规模因子暴露与换手率因子暴露是负相关的，与异常换手率因子有微弱的正相关关系。换手率的计算公式是一定时间内的累计成交额除以流通市值，公式中已经自带去量纲处理，因此可以认为规模因子暴露并不会过多地影响换手率因子的收益情况。目前学术界使用公司特征值代替时间序列回归作为因子暴露，也是因为相比于时间序列回归，公司特征值可以更好地避开某个因子在其他因子上的暴露。

为了进一步规避规模因子的影响，剔除A股流通市值最小的前30%股票之后再做回测，规避市值过低的僵尸企业因借壳上市的炒作带来的“壳污染”问题(见表6)。

表6 单因子选股收益率统计表(剔除市值最小的前30%股票)

可以看出在剔除市值最小的前30%股票之后，换手率和异常换手率因子的选股收益率有所下滑，大致下滑了2～3个百分点。但是两个因子收益率的单调性还是和之前没有提出小市值股票时候保持一致，异常换手率因子依然有着出色的单调性，选择异常换手率最低的股票依然可以获得9.37%的年化收益率，亦即10年6.28倍的资金曲线。

结合Rank IC、IR、历史回测数据可以得出结论，按照量化投资业界的标准，传统的换手率和异常换手率均属于有效因子，相比之下异常换手率的效果更好。

六、结论与启示

利用Fama-Macbeth回归可以发现，换手率和异常换手率因子的收益率是显著的。从量化金融业界的常用指标ICIR可以发现，剔除小市值影响的两类换手率因子均可以获取稳健的超额收益。由此可见，在A股这类新兴市场，基于行为金融学理论构造的因子与基本面因子相关性较低，可以对传统的多因子模型进行有效补充。从行为金融学入手研究实证资产定价模型仍有很大的发展前途。

研究多因子模型不仅可以补充现有的资产定价模型，给投资者带来量化投资的建议，也可以协助监管者分析资本市场的波动与投资者非理性行为之间的关系。这对于构建多层次的资本市场、完善投资者保护政策、实现资本市场的可持续发展，都有重要意义。