山火条件下输电线路跳闸概率计算

刘辉，杨韬，林济铿，王京景，严波，刘潇

(1. 国网安徽省电力有限公司，安徽 合肥 230022；2. 同济大学 电子与信息工程学院，上海 200092；3. 安徽继远软件有限公司，安徽 合肥 230031)

0 引言

中国山地众多，大量的输电线路经过丛林和山区，近些年山火经常导致输电线路跳闸[1-4]，严重影响电网运行可靠性和安全性[5-6]。因此，如何较准确预测山火条件下输电线路跳闸概率以便采取有效预防措施是减少电网事故的关键。

目前，对于山火导致的输电线路跳闸的研究大致包括3方面：山火导致输电线跳闸的机理、山火蔓延机理和跳闸概率计算。

（1）山火导致输电线跳闸的机理研究。目前大多采用实验室试验的方法获得山火导致线路跳闸的机理。文献[7-8]论证了高温条件下火焰温度与相对空气密度的关系，火焰温度越低，激发流注发展所需要的电场强度就越低，相应使得线路绝缘被击穿的电压就越低。文献[9-10]通过实验得出火焰温度与距离地面高度的关系，火焰距离地面高度越高，火焰温度就越低。文献[11-13]采用单股导线、双分裂导线和四分裂导线做实验，证明火焰高温会影响线路平均击穿场强。文献[14-16]通过试验获得线路间隙中带电粒子浓度会因为植被燃烧过程产生的无机盐而提高，导致间隙的电导率增大的结论。文献[17]研究得出植燃烧过程中产生的离子和电子会使火焰呈弱等离子体性质，相应会降低火焰与线路间隙击穿电压，从而导致间隙击穿。植被燃烧产生的颗粒会进入放电通道，间隙放电机理也与一般间隙放电不同[18-19]。目前对于山火条件下输电线路跳闸机理的研究已受到较多重视，但所得到的结论还只是基于实验室试验，有待进一步工程实际验证。

（2）山火蔓延机理研究。目前大多基于Rothermel模型和王正非模型[20-22]，采用仿真策略模拟山火蔓延过程。文献[23]将 Rothermel 模型引入二维元胞自动机模型中，提出了更为准确的山火蔓延过程，但该方法由于其参数之间的多重嵌套关系，略显复杂。文献[24]在元胞自动机蔓延模型中引入了相关因素，使得山火蔓延过程更符合实际。文献[25-26]均建立三维元胞山火蔓延模型，实现了在复杂环境条件下山火蔓延过程的模拟。可以看出，如何更为准确的模拟山火蔓延仍是众多研究人员的关注重点之一。

（3）山火跳闸概率的计算研究。目前这方面的研究尚不多见，只有文献[20]和文献[27]在提出了考虑温度系数[28-29]和浓烟因素的绝缘击穿电压的修正方法之后，进一步提出了忽略植被及当地降雨情况等因素线路跳闸概率的计算方法。文献[30]运用了元胞自动机技术，但考虑因素不全。文献[31]只研究了监测和告警计算。可以看出，如何较为科学地计算山火导致的线路跳闸概率，仍有待提升和拓展。

综上，本文提出基于改进元胞自动机山火蔓延模型的输电线路跳闸概率计算新方法。首先引入火焰温度、植被类型、火点距离和降雨量等因素综合考虑其对输电线跳闸的影响；然后采用改进元胞自动机对山火蔓延过程进行准确的预测，根据其蔓延趋势得到更为精确的山火导致输电线跳闸的概率。

1 影响因子

山火发生时对于附近输电线路的跳闸有一定的影响，其影响机制复杂，迄今并没有系统方法描述和刻画。山火导致线路跳闸的原因包括：火焰温度、当日降雨量、植被可燃率以及火点与线路之间的距离。这几个因素的变化将导致输电线路中的空气间隙绝缘强度发生大幅下降而导致线路放电短路而跳闸。合理地考虑这些因素对于线路跳闸的影响，即可较为准确地计算其跳闸概率。

1.1 火焰温度

线路附近空气环境受植被火焰温度影响，从而引起线路间隙强度变化。火焰温度因子为

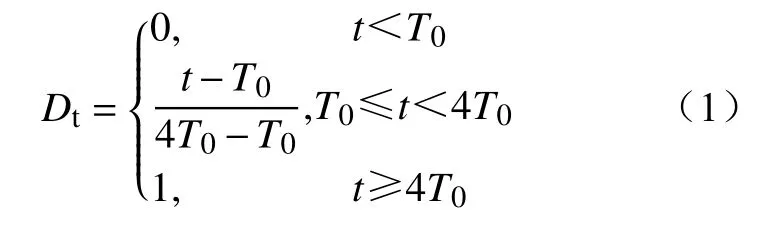
式中：T0为标准大气温度；t为发生山火时大气温度。

1.2 降雨因子

山火的产生和蔓延均与当日降雨量有关，其规律为：在预测地区内过去一小时和未来一小时降雨量均超过3 mm的话，植被被点燃或者火点保持燃烧的可能性几乎为0，山火无法蔓延。因此降雨因子为

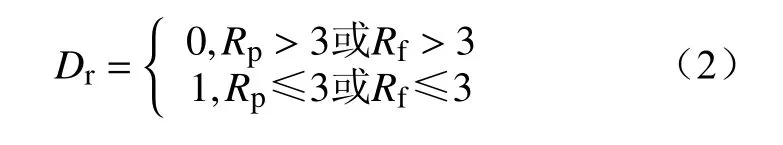
式中：Rp和Rf分别为过去一小时和未来一小时的降雨量。

1.3 植被因子

火点蔓延与火点周围植被类型有关。火点周围环境可划分为可燃区域和不可燃区域，可燃区域分为林木和草原等区域，不可燃区域分为荒漠和河道等区域。因此植被因子Dp根据其类型选择如表1所示。

表1 植被类型Table 1 Vegetation types

1.4 距离因子

只有山火蔓延至输电路下方或者一定范围内，输电线路才有可能跳闸。因此，山火与输电线路的距离也是导致跳闸的一个重要因素。

1.4.1 山火蔓延速度计算

由于山火蔓延速度会受到周围空气环境的影响，其蔓延速度为

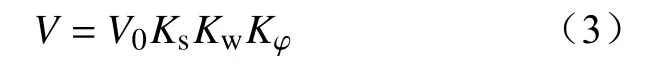
式中：V0、Ks、Kw及Kφ分别为初始蔓延速度，可燃物、风及坡度调整系数。

（1）初始蔓延速度V0的计算。当山火发生在无风和平坦的地表上时，初始蔓延速度为V0。在这种情况下，空气温度与湿度对它影响较大，因此计算表达式为

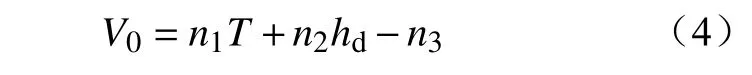
式中：n1=0.03，n2=0.01，n3=0.3；hd为日最小湿度；T为大气温度。

（2）可燃物调整系数Ks。不同植被对山火蔓延速度影响程度不同，可燃物系数Ks取值如表2所示。

表2 植被类型Table 2 Vegetation types

（3）风调整系数Kw。风速大小与风向的变化会对山火蔓延速度产生影响，Kw的计算表达式为

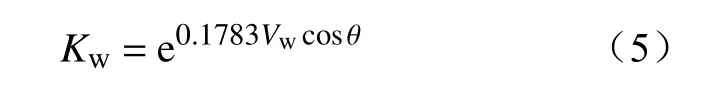
式中：Vw为风速；θ为蔓延方向与风向的夹角。

（4）坡度调整系数Kφ。坡向与坡度大小也会影响山火蔓延速度，上坡会加速山火的扩散，下坡会减缓山火的扩散，Kφ的计算表达式为

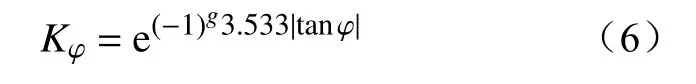
式中：g为坡向标志；当坡向为上坡时，g=0，当坡向为下坡时，g=1；φ为坡度角。

1.4.2 火点离线路初始距离

火点出现时，需要迅速找到与火点较近的输电线路的位置，计算出它们之间的距离。其具体计算过程如下。

（1）邻近网格的确定。

选取如图1所示的网格，边长为4 km，中心点（x’,y’）记作火点，4个顶点记作A、B、C、D，通过计算4个坐标，从而判断出位于网格里的输电线路。

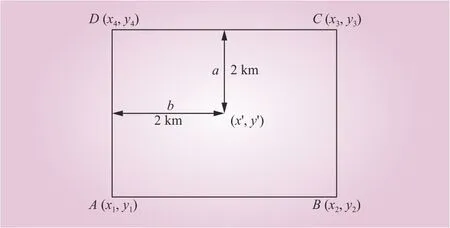
图1 火点网格Fig. 1 Fire grid

1.4.3 寻找网格中的输电线

找到网格内所包括的输电线路，并计算它们与火点的距离。记录网格内所有线路段并标记，设第i段线路中心坐标i（loni,lati），若满足式（11）条件，则表示线路中心坐标处在以火点为中心的网格内，便记录其坐标以便求取与火点距离L。

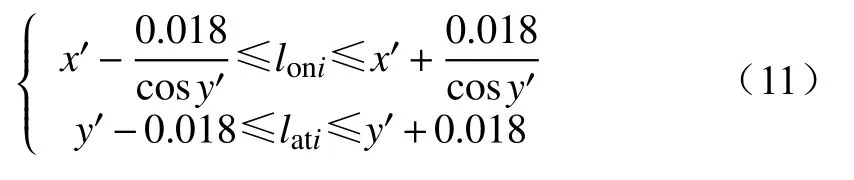
1.4.4 距离因子计算

当线路正下方发生火灾时，往往线路跳闸的概率越大。这是因为线路与火焰的距离不同，火焰对线路周围的空气，电导率以及颗粒的影响也会不同。离火点越近，其跳闸概率也越高。距离因子为

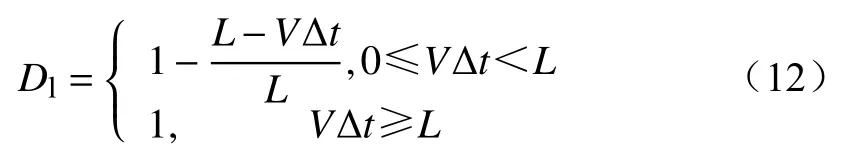
式中： Δt为山火持续时间；L为初始火点与线路中心的距离；V为山火蔓延速度。

2 山火条件下击穿电压修正

温度上升引起的大气压强、密度和湿度变化及烟尘浓度是造成大气环境下气隙绝缘强度下降的主要因素，相应地，在火焰区下，火焰温度、电导率以及颗粒和灰烬是造成气隙绝缘强度下降的主要因素。山火条件下，即使在正常工作电压下，山火蔓延至线路下方时，因线路各相间间隙被击穿而导致的线路相间短路故障时常出现。

2.1 大气环境下击穿电压修正

针对火焰温度以及烟尘引起的击穿电压下降，本文采用大气修正系数Kt和烟尘修正系数Kp计算击穿电压修正值，即

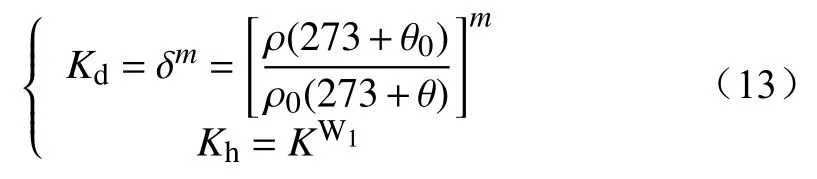
式中：m，W1及K取值可查阅国家标准[28]；δ为空气相对密度； ρ与 ρ0，θ与θ0分别为山火条件下和标准参考大气条件下的大气压强和大气温度。

若整个间隙都充满烟尘浓烟时，击穿电压下降到原击穿电压的1/15，烟尘修正系数为

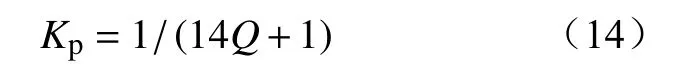
式中：Q为间隙中烟尘浓度，Q=0%表示无浓烟，Q=100%表示充满浓烟。

因此，山火条件下，考虑空气情况的下线路击穿电压需修正为

式中：U0为标准工况下的线路击穿电压；Ua为山火条件下的线路击穿电压。Kt=KdKh，参数Kd、Kh分别为空气密度和空气湿度修正系数。

2.2 火焰区域下击穿电压修正

当山火蔓延至线路下方时，线路的气隙可分为火焰区和非火焰区（烟尘区）。当山火火焰全包络输电线，即火焰充满整个间隙时，间隙在火焰区的击穿特性主要受火焰温度和电导率的影响。而火焰未包络整个间隙时，线路在非火焰区跳闸主要由颗粒和灰烬引起。山火条件下，火焰区域中的击穿电压需修正为

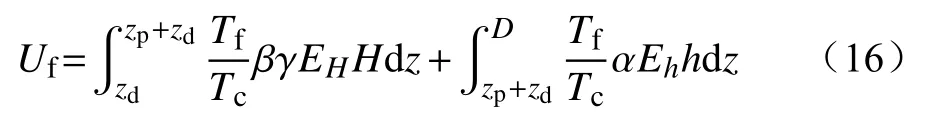
式中：Tf为火焰附近温度；Tc为火焰最高点温度；α为非火焰区的颗粒浮动修正系数；β和γ为火焰区颗粒浮动修正系数和电导率校正系数；h和H为非火焰区间隙长度和火焰区间隙长度；Eh和EH为分别为非火焰区和火焰区的平均击穿电压梯度。Tc为火焰温度随着距离地面高度变化的变化量[29]，即

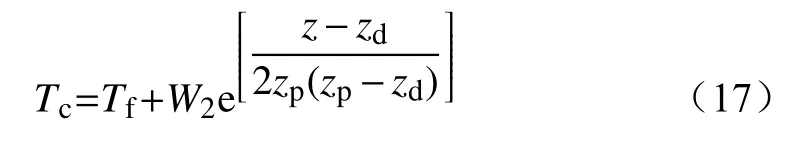
式中：W2为经验常数；zp为火焰高度；zd为植被高度。

综合考虑Ua，Uf山火条件下的击穿电压U最终结果为

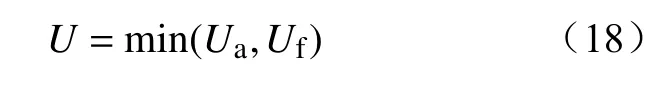
3 山火蔓延模型

合理预测山火过火区域，既能够有效预防山火灾害以及派遣相关人员及时扑救，又可更为准确地预测山火蔓延过程的线路因山火导致的跳闸概率。而元胞自动机模型能较好地模拟山火蔓延，因此本文采用改进元胞自动机算法进行山火蔓延模拟，以准确地预测附近线路的跳闸概率的变化情况。

中心元胞周围元胞的蔓延情况会对其燃烧面积产生影响，周边元胞燃烧状态可分为3种：（1）2个邻胞已燃烧完全，并向中心元胞扩散；（2）1个邻胞1个次邻胞已燃烧完全，并向中心元胞扩散；（3）2个邻胞1个次邻胞已燃烧完全，并向中心元胞扩散。

3.1 中心元胞新增燃烧面积的计算

（1）如图2所示，2个邻胞燃烧完全后的扩散过程，S1为邻胞（i，j−1）对中心元胞的蔓延面积；S2为邻胞（i+1，j）对中心元胞的蔓延面积；S为S1与S2的重叠面积。在时刻t蔓延的图形面积为

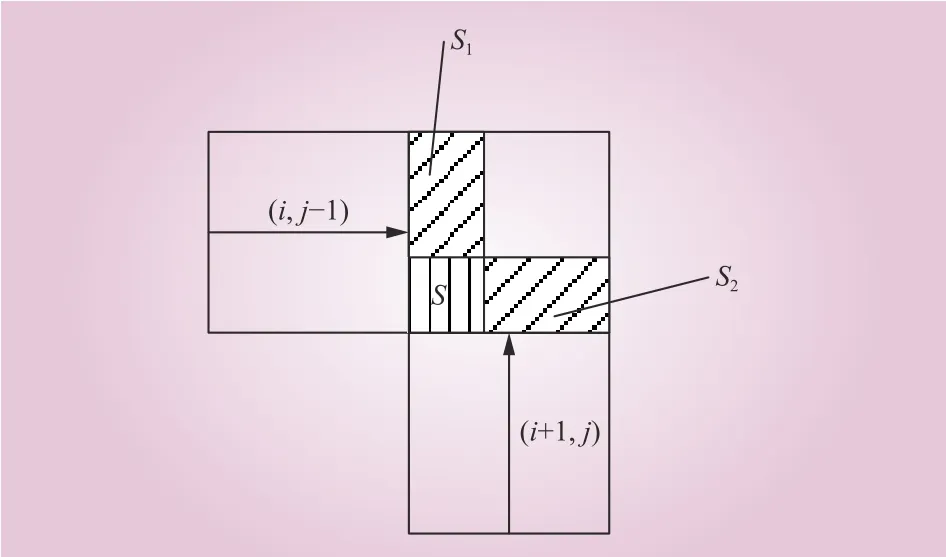
图2 两个邻胞完全燃烧蔓延面积Fig. 2 The completely burned spread areas of two neighbor cells

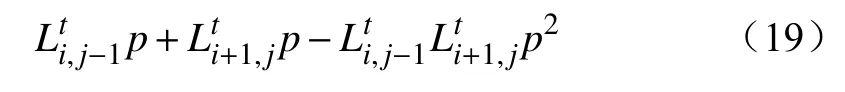
则时间增加 Δt的蔓延面积为

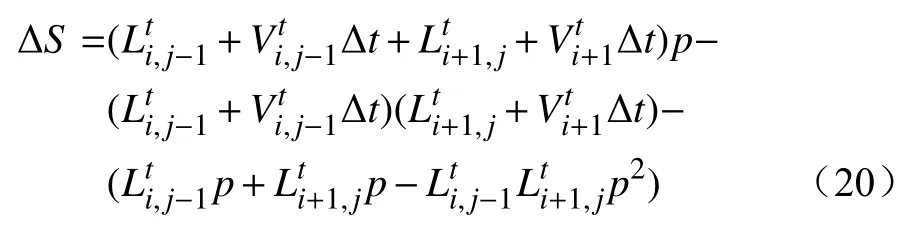
式中：ΔS为蔓延面积增长量；V为某元胞时刻t蔓延速度；L为蔓延面积宽度；p为元胞长度。

（2）由于邻胞和次邻胞蔓延速度不同，1个邻胞和1个次邻胞蔓延可分为几种情形：邻胞蔓延速度较快，导致邻胞蔓延面积完全包含次邻胞蔓延面积；次邻胞蔓延速度较快，导致次邻胞蔓延面积部分超过邻胞蔓延面积。由于现实条件下，2种情况的重叠面积相差不大，为简化过程，均以邻胞蔓延速率大于次邻胞蔓延速率情形处理，如图3所示。

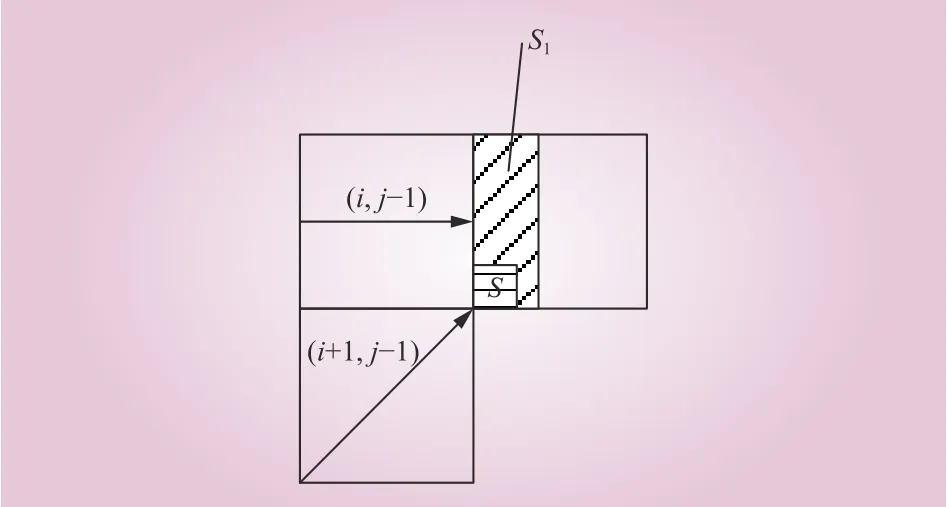
图3 单邻胞蔓延速率超过次邻胞蔓延速率Fig. 3 The spread rate of single neighbor cell exceeds that of the diagonal neighbor cell

在图3的情况下，邻胞蔓延速度超过次邻胞蔓延速度，因此重叠面积S为次邻胞蔓延面积S2。由于邻胞蔓延速度起决定作用，面积增长形状呈矩形，在经过Δt时刻后，蔓延面积ΔS增长为

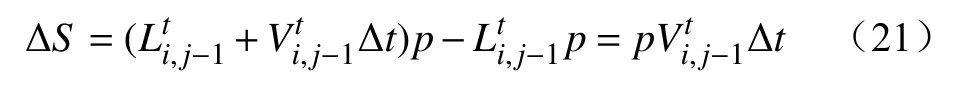
（3）由于邻胞和次邻胞蔓延速度不同，2个邻胞和1个次邻胞蔓延可分为如下情形：邻胞蔓延速度较快，导致邻胞蔓延面积完全包含次邻胞蔓延面积；次邻胞蔓延速度较快，导致次邻胞蔓延面积部分超过邻胞蔓延面积。由于现实条件下，两种情况的重叠面积相差不大，为简化过程，均以邻胞蔓延速率大于次邻胞蔓延速率情形处理，如图4所示。

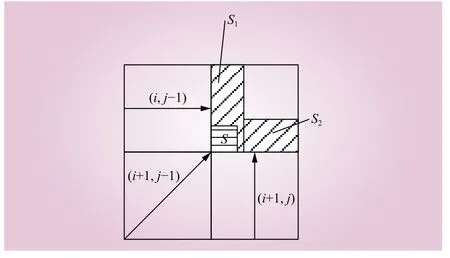
图4 双邻胞蔓延速率超过次邻胞蔓延速率Fig. 4 The spread rate of double neighbor cells exceed that of the diagonal neighbor cell

在图4的情况下，邻胞蔓延速度超过次邻胞蔓延速度，因此重叠面积S为次邻胞蔓延面积S1、S2以及次邻胞蔓延面积S3的重叠部分。在时刻t蔓延的图形面积为

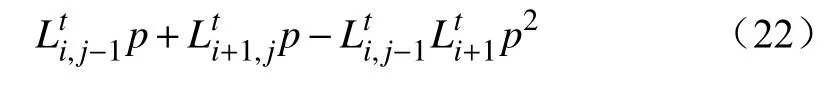
则时间增加Δt的蔓延面积ΔS为

3.2 新增蔓延面积计算规则

首先判断元胞（i，j）周围元胞的山火蔓延状态，对于不包含上文所述3种情况，则按传统元胞自动机计算规则进行处理；若包含上文所述3种情况，则计算规则为

4 山火条件下线路跳闸概率计算

气隙击穿的概率分布符合高斯分布特点[20]，因此在山火条件下气隙击穿概率的概率密度为

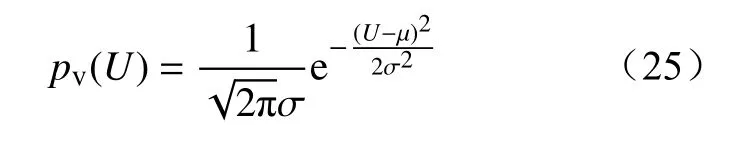
式中：U为修正后的击穿电压，标准差σ=U50zc，均值μ=U50；U50为50%击穿电压；zc为变异系数。因为不同间隙的电场形式和不同类型的击穿电压会导致分散性不同，在正常情况下，空间气隙工频击穿电压的分散性不大，取2%。但考虑山火发生时，颗粒导致空气间隙更不均匀，分散性更大。所以山火发生时，变异系数取4%。

山火条件下线路跳闸概率为

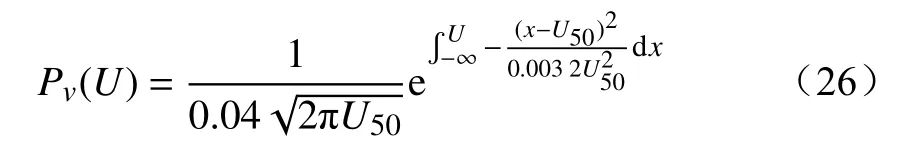
通过山火蔓延模型可以获得山火蔓延边界，选取边界元胞中心为火点坐标，依据第1节所述的邻近网格的概念，标识边界元胞周围的输电线路，计算初始点与标识目标距离L。基于第3节所述的山火蔓延模型，扩展速度为山火蔓延速度V，在综合考虑影响因子的情况下，输电线路综合跳闸概率为

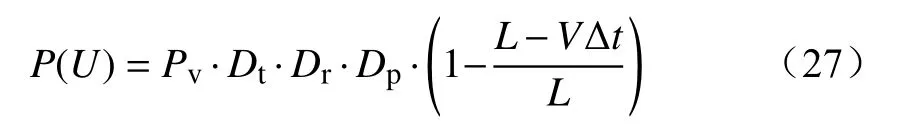
由于常规Pv计算时未能考虑火焰温度、当日降雨量、植被类型以及火点距离对概率计算的影响，所以通过引入影响因子使得计算结果更精确。在日降雨量过大或植被不可燃的条件下，山火无法蔓延至输电线路下方，跳闸概率为0；当满足蔓延条件时，火点与输电线路的距离会影响跳闸概率，蔓延至显露下方时，跳闸概率最高。

5 计算流程

基于本文的输电线路跳闸概率计算方法，其计算流程如图5所示。当出现火点时，通过采集火点坐标以及周边大气环境和地理条件，利用改进的元胞自动机山火蔓延模型对火点扩散区域进行合理预测，对有可能过火范围内的输电线路进行标记；采集被标记输电线路周边大气环境以及地理条件，计算影响因子以及校正击穿电压，最后计算得出各段输电线路跳闸概率。

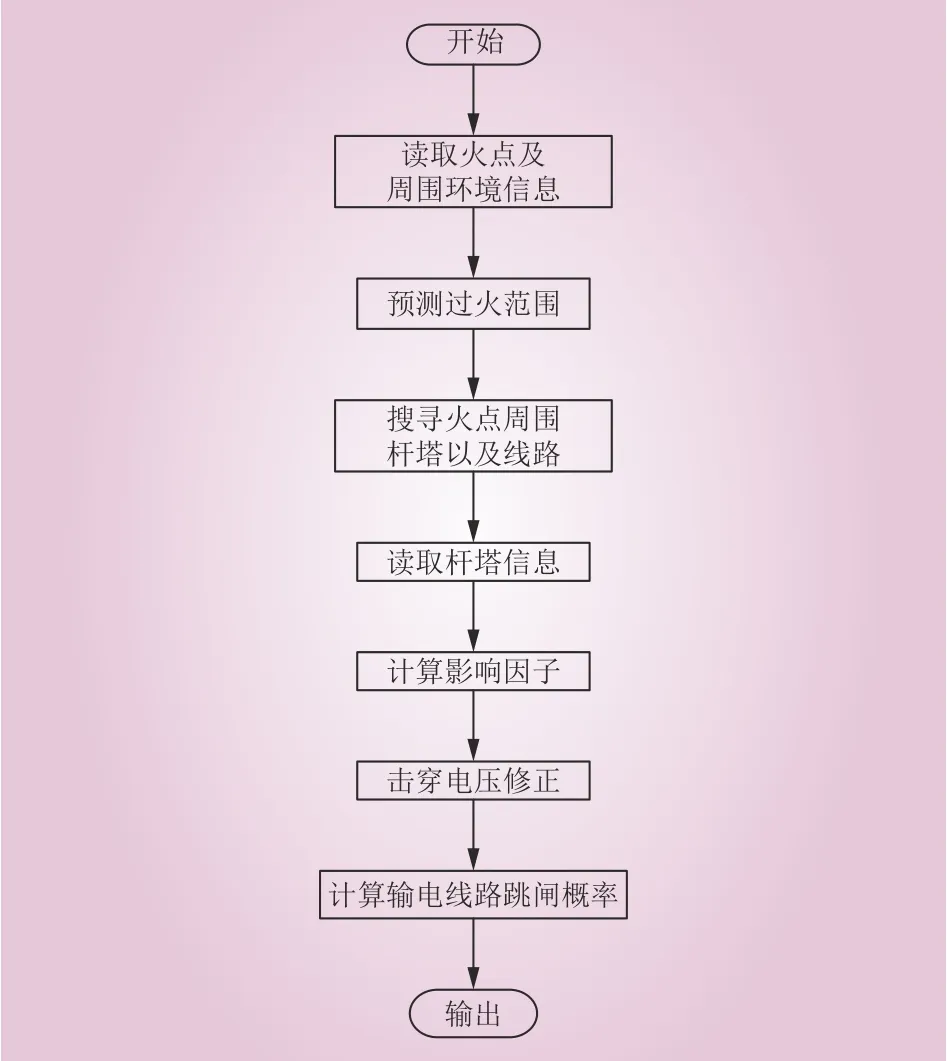
图5 山火条件下输电线路跳闸概率计算流程Fig. 5 Flow chart for transmission line trip probability calculation under forest fire conditions

6 算例分析

6.1 山火蔓延模拟

风速、温度、湿度、坡度以及可燃物均会影响山火蔓延速率。若风速1.5 m/s，气温27°C，相对湿度0.4，坡度30°，可燃物为茅草，根据前文所述计算山火初始蔓延速度计算方法，初始蔓延速度R0=0.59 m/min；场地为二维正方形200×200 m，元胞大小为1×1 m。设置火点元胞（100,100），输电线路在火点下方20 m处，并模拟山火蔓延100 min的蔓延情况。

图6和图7分别表示蔓延60 min和100 min后的山火蔓延情况。改进算法得出红色部分，传统算法得出黑色部分。可以看出改进区域实际上是蔓延的面积更小。图6和图7中的黑色X记号表示输电线位置。可以看到，由于传统算法的计算缺陷会导致模拟时，山火过早进入输电线路下方，相应其跳闸概率也偏大。而改进算法能够改善这种情况，使得山火蔓延计算可信度更高，工作人员可根据预测的蔓延地区标记出区域内的输电线路，随时做好停运相关线路的准备。

图6 山火蔓延60 minFig. 6 The forest fire spreading for 60 minutes

图7 山火蔓延100 minFig. 7 The forest fire spreading for 100 minutes

6.2 山火条件下线路停运概率

本文输电线路采用500 kV交流双回线输电线路为对象，线地距离为13.6 m，工频击穿电压为4 100 kV。在以茅草为可燃物，烟尘浓度为100%以及降雨量小于3 mm条件下，计算不同情况下的线路跳闸概率。

图8表示不同温度下，输电线路跳闸概率随着火焰高度的增长（即火焰区不同）而变化的情况。能够看出，跳闸概率的增长与火焰高度呈正比。火焰温度越高，输电线距离火焰区越近，击穿电压越低，线路跳闸概率就越高。

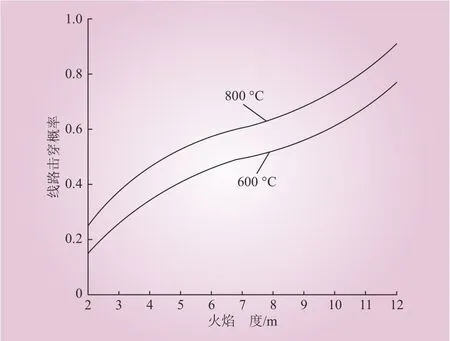
图8 火焰高度与线路跳闸之间的关系Fig. 8 The relationship between flame height and line trip probability

图9表示不同温度下，输电线跳闸概率随着火点与输电线距离变化而变化的情况。线路的跳闸概率随着火点与线路之间距离的减小而增大。

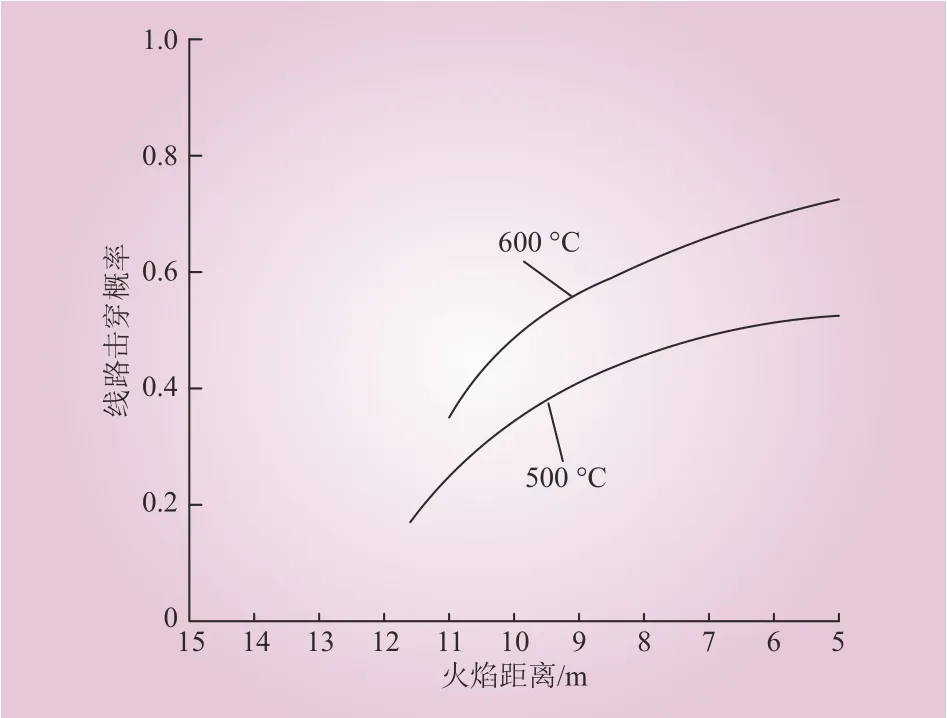
图9 火焰距离与跳闸概率之间的关系Fig. 9 The relationship between flame distance and line trip probability

从图8和图9可以看出，山火条件下，其线路跳闸的概率受到多种因素影响。当温度相同时，火点距离越近，火焰高度越高时，输电线路跳闸概率越大；当火点在线路正下方时，火焰温度越高，火焰高度越高，输电线路跳闸概率越大；当火焰高度相同时，火焰温度越高，输电线路跳闸概率越大。

7 结语

针对山火条件下输电线路的跳闸特性，引入火焰温度、植被类型、火点距离和降雨量等因素综合考虑对输电线跳闸的影响；然后采用改进元胞自动机对山火蔓延过程进行准确的预测，根据其蔓延趋势得到精确的山火导致输电线跳闸的概率。本文线路跳闸概率模型较为全面地考虑了山火跳闸的各种因素，并考虑山火的蔓延趋势，相应较为准确地给出了实际山火条件下的输电线路的跳闸概率计算。本文所建立的模型及算法可对在山火条件下线路跳闸进行预警，工作人员可根据预测的蔓延地区标记出相关线路，利用概率计算得到跳闸概率较高的线路，并针对线路跳闸设计电网安全运行方案，使得系统运行更安全可靠。