基于软件可量化计算的绿色建筑能耗控制仿真

王 芳，郭秀娟

(1. 吉林建筑科技学院管理工程学院，吉林 长春 130114；2. 吉林建筑大学电子信息与计算机学院，吉林 长春 130118)

1 引言

绿色建筑是将绿色理念应用在建筑的设计、规划和施工中，由第三方在指标评定标准的基础上完成建筑绿色度的认证和管理[1]。绿色建筑的目标为建设新型的建筑体，实现生态、经济和效益的结合，将当地特色资源和先进的技术成果应用在绿色建筑中[2]。在社会不断发展下人们对工作环境和居住环境提出了更高的舒适要求。为满足人们的需求，建筑的能耗不断增加。在社会能耗中我国建筑能耗占据1/3，并呈现持续增加趋势，因此需对绿色建筑能耗控制方法进行进一步分析和研究。

李林涛等人[3]提出基于逆向建模的绿色建筑能耗控制方法，该方法分析服务参数和室外温度对建筑能耗产生的影响，并拆分拟合建筑总能耗，在拟合参数的基础上构建能耗评价模型，根据评价结果控制绿色建筑能耗。但是该方法计算得到的权重稳定性较差，无法准确地预测建筑能耗组成。陈虹宇等人[4]提出基于信息化设计的绿色建筑能耗控制方法，该方法分析建筑可视度、光环境和风环境，根据分析结果构建评价指标体系和评价模型，对建筑能耗进行评价，根据评价结果对能耗进行控制。但是该方法没有对评价指标权重进行修正处理，预测的平均年能耗密度存在误差。李叶红等人[5]提出基于二次平均法的建筑能耗控制方法。该方法对建筑能耗的分布特征进行分析，通过二次平均法在能耗分布特征的基础上对建筑能耗进行评价，实现建筑能耗控制。该方法没有对评价指标进行量化处理，获得的评价结果误差较大，存在控制效果差的问题。

为解决上述方法中存在的问题，提出基于软件可量化计算的绿色建筑能耗控制新方法。

2 指标体系构建

对绿色建筑能耗的控制之前需要确定能耗影响因素，并分析因素之间存在的关系。基于软件可量化计算的绿色建筑能耗控制方法根据一定方法和规律按照影响因素的性质、客观因素和主观因素区分影响绿色建筑能耗的因素。

地理位置、天气和人文等影响因素的主观性较强，很难对其实现量化处理，客观因素可以进行量化分析，包括设备的使用状况、建造材料和建筑本身的属性等[6]。基于软件可量化计算的绿色建筑能耗控制方法为避免主观因素在能耗评价中的随机性，主要对客观因素进行分析。客观因素按照指标体系建立原则分为建筑设备及动力系统、围护结构和建筑规划三类。

确定绿色建筑能耗评价指标后，采用AHP法对指标进行量化处理：

对绿色建筑能耗评价指标进行划分，将其分为三个层次，分别是指标层、准则层和目标层[7]。

在专家意见的基础上分析评价指标对绿色建筑能耗的影响程度bij，根据分析结果构建判断矩阵，计算评价指标对应的权重，即在各个元素下分配绿色建筑能耗评价指标的权重。

利用影响程度bij构建判断矩阵Bk，其表达式如下

(1)

设W、λmax分别代表判断矩阵的特征向量和最大特征根。在满足一致性要求的基础上，根据矩阵理论可知，判断矩阵中存在非零的唯一最大特征根λmax=n，除此之外其余特征根在判断矩阵中的值均为零。因此可以通过判断矩阵的特征向量W和最大特征根λmax计算绿色建筑能耗评价指标对应的权重[8]。

假设判断矩阵B为n阶的，通过计算其特征向量W和符合BW=nW的特征根，获得绿色建筑能耗评价指标对应的权重，最大特征根λmax可通过下式计算得到

(2)

式中，(BW)i描述的是特征向量W与判断矩阵B乘积中存在的第i个元素。

为了提高分析结果的合理性，需要一致性检验判断矩阵，在判断矩阵B中计算除λmax之外所有特征根对应的负平均值，并将计算结果CI作为标准，检验判断矩阵的一致性

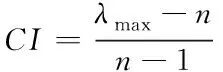
(3)

分析上式可知，判断矩阵的一致性随着λmax-n值的减小而增大，当λmax-n的值为零时，B的一致性最佳。

设CR代表随机一致性比率，其计算公式如下

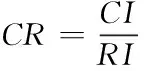
(4)

式中，RI代表判断不同阶数判断矩阵是否符合一致性的随机一致性指标。

当CR的值大于0.1时，需要修改调整判断矩阵；当CR的值小于0.1时，表明判断矩阵通过一致性检验[9]。

为了提高指标权重计算结果的稳定性，基于软件可量化计算的绿色建筑能耗控制方法采用群体性判断原则扩大样本数据的来源。

采用信息熵权法通过熵值修正绿色建筑能耗评价指标的权重，获得绿色建筑评价指标的修正权重W2，具体过程如下：

标准化处理权重矩阵W=(wij)m×n，获得判断矩阵A=(rij)m×n，其中rij描述的是数据经过标准化处理的结果。

设Hj代表修正系数，其计算公式如下

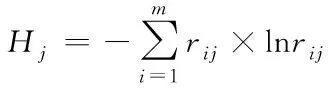
(5)

根据修正系数Hj建立权重修正模型

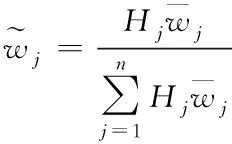
(6)

3 绿色建筑能耗评价模型

基于软件可量化计算的绿色建筑能耗控制方法在可变模糊基理论的基础上构建绿色建筑能耗评价模型，根据评价结果实现绿色建筑能耗的控制，具体过程如下：

1)设Xi代表待评价的绿色建筑；n代表绿色建筑能耗评价指标的数量；Xi={x1，x2，…，xn}代表特征向量，由绿色建筑能耗指标的样本值构成，X={Xi}，xij描述的是第i个绿色建筑评价指标在第j个样本中的特征值，由xij构成待评价的绿色建筑样本特征值矩阵X，其表达式如下

(7)

式中，m描述的是绿色建筑能耗评价指标的数量，i=1，2，…，m，j=1，2，…，n。

2)按c个等级对评价等级划分，一级为最好，根据评价等级对每个绿色建筑能耗评价指标进行划分，获得c个区间，建立评价区间矩阵Iab，其表达式如下

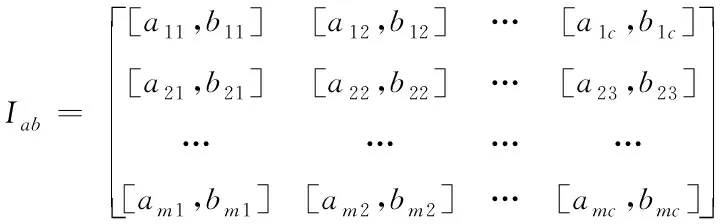
(8)

式中，[a，b]描述的是吸引域区间。

3)设Icd代表可变范围区间矩阵，可根据评价区间矩阵Iab计算得到

(9)

其中，区间[cih，dih]可通过下式计算得到

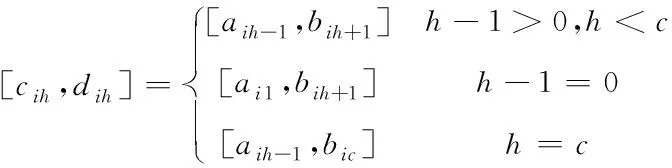
(10)

4)按照各个绿色建筑能耗评价指标的具体情况，根据评价区间矩阵Iab确定隶属度为1的点在区间[aih-1，bih+1]中对应的值，设矩阵M由隶属度为1的点构成，其表达式如下

(11)

当特征值xij落在Mih值的左侧和右侧时，对应的隶属函数如式(12)和式(13)所示

(12)

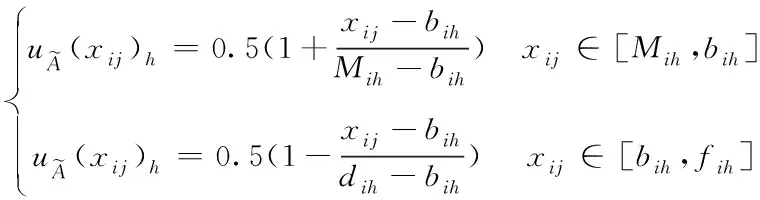
(13)

根据式(12)和式(13)的计算结果，构建隶属矩阵{u(Xj)}：

(14)

5)在隶属矩阵{u(Xj)}的基础上构建可变模糊综合评价识别模型，其表达式如下

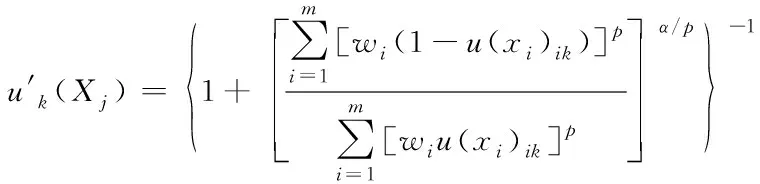
(15)

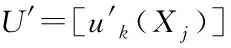
6)计算待评价绿色建筑样本j对应的级别特征值H=(1，2，…，c)·UT，实现可变模糊识别。

8)根据评价结果，实现绿色建筑能耗的控制。

4 实验与分析

为了验证基于软件可量化计算的绿色建筑能耗控制方法的整体有效性，需要对基于软件可量化计算的绿色建筑能耗控制方法进行测试。本次测试的实验平台为Simulink，分别采用基于软件可量化计算的绿色建筑能耗控制方法(所提方法)、基于逆向建模的绿色建筑能耗控制方法(文献[3]方法)、基于信息化设计的绿色建筑能耗控制方法(文献[4]方法)对绿色建筑能耗的照明能耗、供暖能耗、制冷能耗和风机能耗进行预测，预测结果如图1所示。

图1 能耗组成预测结果

分析图1中的数据可知，采用所提方法对绿色能耗的照明能耗、供暖能耗、制冷能耗和风机能耗进行预测时，获得的预测结果与实际结果基本相符，采用文献[3]方法对照明能耗、供暖能耗、制冷能耗和风机能耗进行预测，获得的预测值均小于实际值，采用文献[4]方法对照明能耗、供暖能耗、制冷能耗和风机能耗进行预测，获得的预测值均高于实际值。通过上述分析可知，所提方法可准确地对照明能耗、供暖能耗、制冷能耗和风机能耗进行预测，因为所提方法计算绿色能耗评价指标的权重时，采用群体性判断原则扩大了样本数据的来源，提高了权重的稳定性，进而提高了预测的精准度。

分别采用所提方法、文献[3]方法和文献[4]方法对绿色建筑能耗的平均年能耗密度进行评价，测试结果如图2所示。

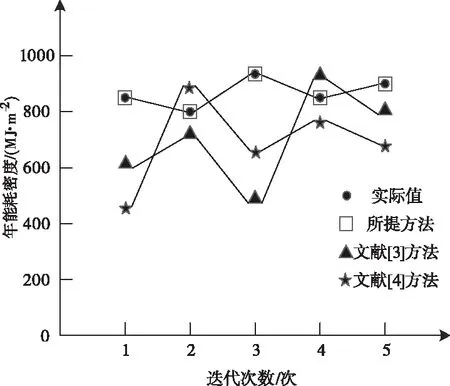
图2 平均年能耗密度测试结果

根据图2中的数据可知，在多次实验过程中，所提方法获得的年能耗密度值与实际值完全一致，文献[3]方法和文献[4]方法获得的年能耗密度值与实际值之间存在的误差较大。因为所提方法对绿色建筑能耗评价之前，通过信息熵权法对绿色建筑能耗评价指标的权重进行了修正，进而提高了绿色建筑能耗评价模型的精度，可准确地对绿色建筑能耗的平均年能耗密度进行评价，验证了所提方法的有效性。

通过能耗累积频率分布曲线验证所提方法、文献[3]方法和文献[4]方法的控制有效性，测试结果如图3所示。

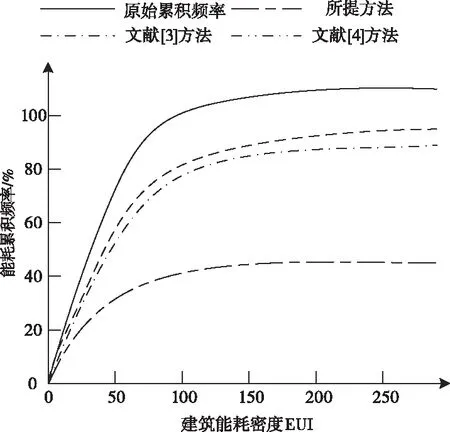
图3 累积频率分布曲线

根据图3中数据可知，采用所提方法对绿色建筑能耗进行控制后能耗累积频率曲线明显下降，表明采用所提方法对绿色建筑能耗控制后，建筑的能耗明显降低，采用文献[3]方法和文献[4]方法对绿色建筑能耗进行控制后，能耗累积频率曲线虽然降低但幅度较小，表明文献[3]方法和文献[4]方法对绿色建筑能耗控制的有效性较差，因为所提方法对绿色建筑能耗评价指标值进行了修正，在此基础上构建了高精度的绿色建筑能耗评价模型预测绿色建筑的能耗，根据预测结果可有效的控制绿色建筑能耗。

5 结论

为响应可持续发展理念，控制绿色建筑能耗。由于目前绿色建筑能耗控制方法无法准确地预测绿色建筑的能耗组成、平均年能耗密度，存在控制效果差的问题。提出基于软件可量化计算的绿色建筑能耗控制方法，选取绿色建筑能耗评价指标并计算指标权值，构建绿色建筑能耗评价模型，根据评价结果实现能耗控制，解决了目前方法中存在的问题，为我国绿色建筑的发展提供了保障。