去噪处理下的复杂网络聚类优化模型研究

姜广坤，裴洲奇

(大连海洋大学应用技术学院，辽宁 大连 116300)

1 引言

复杂网络是描述复杂系统的重要工具，对研究复杂系统具有较大的推动作用[1-2]。通过复杂网络的研究，人类可以更好地掌握和了解互联网的发展特点。21世纪是信息时代，互联网对国家的经济发展和国防建设等方面都产生了巨大的影响，更是与人类的生活密不可分。

现阶段，复杂网络的构建成为当前的研究热点，但是仍然存在很多问题需要相关专家进一步进行探索，例如加权复杂网络聚类结果不准确以及运行速度较慢等。为此，国内相关专家进行了大量研究，同时给出了一些较好的研究成果，例如郭圣等人[3]在深度自编码器中加入空间聚类的“自我表示”特性以及加权稀疏表示，进而实现空间聚类。段佳勇等人[4]通过自适应算法组建无标度网络改进模型，根据计算获取关联度的最优值和网络参数取值，进而获取理想的网络模型。同时进一步对自适应算法中的关联度进行数据学分析，进而实现网络模型聚类。在以上两种模型的基础上，提出一种基于空间关联性的加权复杂网络聚类模型。经实验测试结果表明，所提模型不仅可以有效提升聚类质量和聚类精度，同时还可以提升聚类速度。

2 加权复杂网络聚类方法

2.1 基于空间关联性的加权复杂网络数据去噪

针对不规则的网络构建投影高度图，建立局部三维坐标系，将邻域点集投影至坐标系中，进而获取投影高度。同时，对复杂网络的几何特征进行编码，获取较好的去噪效果[5-6]。

针对加权复杂网络中随机一个节点i而言，需要优先对三维空间的局部领域进行检索，使用K近邻检索，根据点的初始法向计算法向张量投票矩阵U(q(i))，如公式(1)所示：

(1)

上式中，Xn代表标准差；oi和oj分别代表节点i和节点j的高斯权重系数；q(i)代表节点i的法向信息；N(i)代表特征值。

通过公式(1)对加权复杂网络的特征进行分解，获取对应的特征值，将全部特征向量进行两两相交。

当建立好局部坐标系之后，需要将邻域点投影到平面xy上，同时计算各个节点i的投影高度以及投影坐标。为了有效避免投影高度出现负值的情况，需要将节点i和节点j的最大距离作为偏差加到高度值上。所以，采用公式(2)和公式(3)表示投影高度I(j)以及投影点坐标q(i，j)：

(2)

(3)

当得到邻域中全部点的投影高度之后，需要形成规则的高度图像，优先设定高度图像的长和宽，同时将图像放置到坐标系中，进而获取坐标系原点的三维坐标qc，如公式(4)所示：

(4)

当得到像素点的三维坐标以及投影点的三维坐标之后，需要采用高斯插值来计算高度图像中各个像素的强度值I(c)，如公式(5)所示：

(5)

上式中，β代表距离像素点。

将卷积神经网络应用到加权复杂网络数据的噪声滤除中[7-8]，主要采用基于法向滤波的卷积神经网络，优先将组建的高度图作为网络的输入，高度图对应的节点即为输出。卷积神经网络学习是通过高度图获取法向映射，进而输出滤波后的方向，使用L2损失对卷积神经网络进行优化，具体的计算式如下：

loss=(O(p)-O(g))2

(6)

上式中，O(p)代表原始网络数据中包含的噪声；O(g)代表噪声数据的法向。

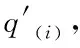
(7)

上式中，α代表固定的权重系数；(xa，xb)代表原始坐标位置。

另外，在网络训练的过程中，需要对训练数据进行预处理操作。同时为了避免空间坐标产生的影响，需要将全部网格都平移到以质心坐标为原点，同时对全部坐标进行标准化处理，将网格的平均边长设定为单位长度，有效降低坐标尺度之间的差异性。

将加权复杂网络中数据的空间相关性关系进行数字化描述，同时采用相关节点代表网络中传感器节点所在的坐标，通过相关系数描述不同感知数据之间的相关度，进而获取加权复杂网络中的空间相关性：

(8)

上式中，θi，j代表数据的空间相关性；cov(di，dj)代表传感器节点坐标。

通过上述分析，需要对卷积神经网络结构进行分析，获取对应的编码局部几何结构，同时通过加权复杂网络各个邻居之间感知数据的关联性进行噪声过滤，并且采用坐标更新算法调整噪声点位置，实现复杂网络数据去噪[11-12]，具体如公式(9)所示：

(9)

2.2 加权复杂网络聚类模型

为了更好理解加权复杂网络，以下给出网络中的相关参数：

1)度分布：

通过网络中节点的度来对各个节点之间的关联关系进行衡量，进而获取节点总数；度分布用来描述网络度的具体分布情况。

2)平均路径长度：

平均路径长度主要用来描述网络中随机一个节点到其他节点的平均距离，具体的计算式如下：

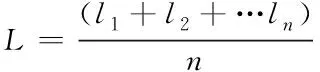
(10)

上式中，L代表平均路径长度；n代表路径总数。

平均路径长度在加权复杂网络连通的情况下有效，但是在大部分情况下网络并不是连通的。为了有效应对上述情况，以下采用一种全新的定义，具体如公式(11)所示：

(11)

上式中，F代表加权复杂网络的全局效率；eij代表路径上的边集合。

3)聚类系数：

聚类系数是用来描述加权复杂网络中各个节点的聚集程度，其中节点i的聚类系数可以表示为公式(12)的形式：

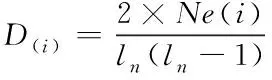
(12)

上式中，D(i)代表聚类系数；Ne(i)代表节点邻居间的真实边数。

4)度相关系数：

代表度和度之间的相关性，主要用来描述节点之间的连接倾向，当大度节点更加倾向于连接大度节点，则说明网络是正相关的；反之，则说明网络是负相关的。其中，度相关系数对应的计算式如下：

(13)

上式中，s代表度相关系数；m代表加权复杂网络的总边数。

5)节点强度：

节点强度主要用来描述有权网络中节点连通情况。其中，节点强度计算式为：

(14)

将加权复杂网络中的数据从输入空间非线性映射到特征空间，与线性子空间相比，一个特征子空间可以使用一组正交基向量表示，则特征值可以表示为公式(15)的形式：

(15)

上式中，G(I)代表特征值；〈xi，I〉代表网络参数。

多维独立成分分析属于一种线性生成模型[13-14]，因此可以将加权复杂网络数据的对数最大似然函数log2L(It(x，y)，t(i)(x，y))表示为以下形式：

log2L(It(x，y)，t(i)(x，y))

(16)

上式中，p〈xi，t〉代表可观测网络参数；det(i，j)代表概率密度。

在多维独立成分分析过程中，可以认为权值参数是正交的，所以需要选择合适的概率密度构建聚类模型，其中概率分布可以表示为公式(17)的形式：

(17)

当独立空间分析被应用于加权复杂网络中，同时将在子空间中投影的范数设定为网络的输出单元，其中网络第一层神经元的激活函数可以采用平方函数；第二层神经元的激活函数采用平方根函数。

近几年，随着高等教育、医疗卫生、科学研究等事业的迅猛发展，国家和地方政府经费的投入逐年增加,大量的资金被用于资源性基础条件建设，通过购置、研制、改造等渠道，大型设备设施数量明显上升。2018年5月，国家卫生健康委员会、国家药品监督管理局印发了《大型医用设备配置与使用管理办法》，从配置、使用、监督等方面，对促进大型医用设备合理配置和有效使用提出要求；财政部、教育部、科技部等部门也通过联合评议、工作评比等形式，不断推动规范和加强大型设备的使用。大型设备都比较昂贵、紧缺，普及率低，如何在保证设备安全使用的前提下，加强大型设备使用绩效管理，提高使用效率，是各单位共同关注的话题。

设定复杂网络的随机样本输入数据为Jt，则加权复杂网络的带权输入可以表示为公式(18)的形式：

(18)

(19)

上式中，wij代表网络参数权值。

通过多维独立成分分析可以有效提取加权复杂网络的特征，为了获取更加满意的性能，需要将原始网络数据的先验子空间信息加入到网络中，进而获取网络数据的本质特征。其中，加权复杂网络对应的损失函数可以表示为公式(19)的形式：

(20)

在对公式(20)进行求解的过程中，需要优先获取加权复杂网络的先验空间子信息。同时采用谱聚类算法构建加权复杂网络聚类模型，通过模型进行聚类[15]，详细的操作步骤如图1所示：

图1 加权复杂网络聚类模型建立流程图

1)设定网络参数，同时将数据集输入到加权复杂网络中。

2)对网络中的权值进行初始化处理。

3)通过计算构建先验信息矩阵。

4)将数据输入到加权复杂网络中。

5)计算网络输出和梯度，如公式(21)所示：

(21)

上式中，r(i)代表网络输出值；c(i)代表梯度值。

6)对梯度值进行更新。

7)通过谱聚类算法构建加权复杂网络聚类模型。

8)采用随机梯度下降法对加权复杂网络聚类模型进行训练，进而输出加权复杂网络的聚类结果。

3 仿真实验

为了验证所提基于空间关联性的加权复杂网络聚类模型的有效性，需要进行仿真实验测试。将文献[3]模型和文献[4]模型作为对比方法，将聚类精度作为测试指标，分析三种聚类模型在不同数据集上的聚类性能，详细的实验测试结果如图2所示：

分析图2中的实验数据可知，与另外两种聚类模型相比，所提模型可以获取更高的聚类精度，主要是因为所提模型对加权复杂网络数据进行了去噪处理，有效滤除数据中的噪声，使聚类精度得到有效增加。

为了进一步验证不同聚类模型的性能，选取聚类实际运行时间作为测试指标，详细的实验测试结果如图3所示：

图3 实际运行时间对比结果

分析图3中的实验数据可知，随着迭代次数的不断增加，各个聚类模型的实际运行时间也开始呈上升趋势。但是与另外两种模型相比，所提模型的实际运行时间明显更低，说明所提模型可以以更快的速度完成网络聚类。

为了验证所提模型的收敛性能，选取聚类质量(Q-value)作为测试指标，分析三种不同模型的聚类性能，详细的实验测试结果如表1所示：

表1 不同模型Q值测试结果对比

通过对表1中的实验数据进行分析可知，Q值会随着迭代次数的增加而增加。所提模型的Q值明显高于另外两种模型，说明所提模型可以获取较高的聚类质量。

4 结束语

为了获取更加满意的聚类结果，提出一种基于空间关联性的加权复杂网络聚类模型。和已有模型相比，所提模型可以有效提升聚类结果的准确性，同时还能够减少聚类实际运行时间，增强聚类质量。

所提模型现阶段已经得到十分广泛的应用，但是仍然存在很多问题需要进一步改进：

1)对先验信息矩阵维度进行改进，全面提升计算结果的准确性。

2)将其应用到多视角的任务分析中，检验是否可以获取满意的聚类结果。