基于去噪优化的动力系统关键参数辨识算法

房怀媛，杨中艳

(临沂大学，山东 临沂 273400)

1 引言

当前对于系统辨识问题的研究，主要是把离散系统当作对象实施参数估计，已经发展出了一整套研究方法和理论体系。随着数字电子与计算机等技术功能的不断强大与成本的逐渐降低，在控制系统领域，越来越多的工程技术工作者与研究人员开始追求纯数字化目标，使离散系统辨识问题获得了极大发展[1]。而与之相对的连续系统辨识问题则研究者整体较少。然而离散差分系数仅具备数学方面的含义，无法像连续系统对应的微分方程一样在物理上提供解释。这使连续模型辨识在近年来受到了越来越多的重视。当前的连续系统模型很多是针对离散模型实施相对变换而获得，然而后移算子仅在离散模型中存在算符，因此这种方式很容易产生信息丢失从而带来一定误差。具体来说，这种方式存在下列问题：会消除一些先验知识、可能出现数值敏感问题、容易出现不良的相位特性、无法反映相对阶次信息、系统稳定性会被改变、技术上存在困难[2]。针对以上问题，对动力学系统的参数辨识问题进行研究，为工业装备的特性动态辨识提供一些实用的方法。

对于动力学系统参数辨识问题的研究，目前有三种传统算法有着比较广泛的应用。一种是国外学者提出的基于等价准则的动力学系统参数辨识算法，这种方法主要基于等价准则思想对动力学系统参数辨识算法进行设计，实现其参数辨识。一种是国内学者提出的基于非线性定位的动力学系统参数辨识算法，该方法主要通过非线性定位算法设计参数辨识算法，对动力学系统进行参数辨识。还有一种是国内学者提出的数值模拟下的动力学系统参数辨识算法，该方法主要通过数值模拟方法进行参数辨识算法的设计。由于这三种传统方法存在辨识精度与辨识速度较低的问题[3-5]，因此，提出一种基于调制函数法的动力学系统参数辨识算法，解决上述问题。

2 算法设计

2.1 噪声处理

对模型噪声进行表示与替换，基于调制函数法构造辨识模型，通过递推算法对辨识模型进行处理以实现噪声的处理。将模型噪声用下式来表示：

e(k)=C(q-1)vy(k)+D(q-1)vu(k)

(1)

式(1)中，e(k)表示模型噪声；C(q-1)vy(k)表示输入端噪声测量的线性组合；D(q-1)vu(k)表示输出端噪声测量的线性组合。

由于式(1)形式较为复杂，通过辨识离散模型时的最小二乘增广估计原理对模型噪声进行替换，具体替换结果如下式所示：

E(k)=(1+c1q-1+c2q-2+…+ciq-i)ε(k)

(2)

式(2)中，ε(k)表示白噪声；ciq-i表示第i个滤波输出；ci表示滤波系数。

将模型噪声直接简化为白噪声的单位滤波输出，通过这种方法能够对模型噪声进行最大简化。通过式(2)替换式(1)的模型噪声，基于调制函数法构造辨识模型，具体如下式所示：

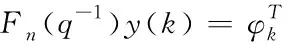
(3)

式(3)中，Fn(q-1)y(k)表示y(k)信号的i次微分调制函数；φk表示待辨识参数；T表示调制函数的间距；ϑ表示调制积分。

其中，调制积分的计算公式具体如下：

ϑ=[a1，a2…，an，b1，b2，…，bm，c1，c2…，cnc]T

(4)

式(4)中，an、bm、cnc表示不同的积分项。

待辨识参数的计算公式具体如下：

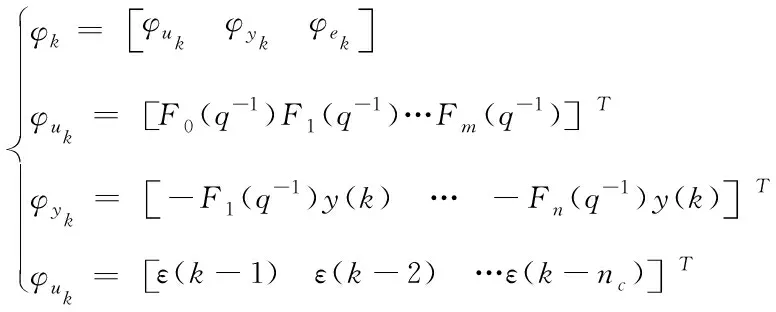
(5)

式(5)中，φuk、φyk、φek分别表示三种信号的待辨识参数。其中，φek中的分量均为未知的，因此，通过估计值对其分量进行代替，具体如下式所示：

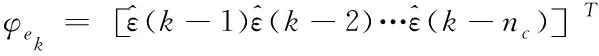
(6)

可以通过已知的、过去的参数估计量对估计误差进行计算，具体如下式所示：

(7)

(k)=[∑lk=1φkφTk]-1[∑lk=1φkFn(q-1)y(k)]

(8)

式(8)中，l表示最小二乘次数[6]。

通过递推算法对辨识模型进行处理，具体处理步骤如下：

1)传送数据。

2)设置初始值，具体公式如下：

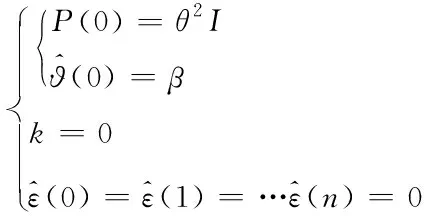
(9)

式(9)中，β表示实向量；P(0)、(0)表示初始条件；I表示单位阵；k表示递推次数。

4)对是否满足停机准则进行判断，停机准则具体如下式所示：

(10)

5)当不符合要求时，转到第3)步，直到满足要求以后即可停止运算。

2.2 构建动力学系统模型

构建动力学系统模型对于参数辨识来说是一个重要的过程，构建的动力学系统模型为行为模型[8]，具体如图1所示。

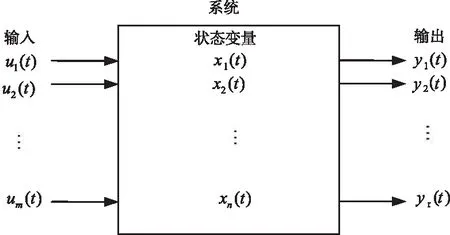
图1 动力学系统模型

2.3 构建参数辨识模型

为构造出与动力学系统模型相一致的参数辨识模型，基于上一节构造的模型构造参数辨识模型[9]。构造时需要遵循以下原则：

1)放宽对于激活函数的要求，也就是在参数辨识模型的神经网络拓扑结构中，激活函数为对各输入实施任意运算后所对应的函数，具体如下式所示：

Y=f[φ(X)]

(11)

式(11)中，Y表示网络输出；φ(X)表示任意函数；X表示网络输入；f(k)表示激活函数。

2)激活函数采用的是f(x)=x，偏差b的取值为0。

3)网络权值可以取待辨识的系统参数或系统参数函数[10]。

根据以上原则构建的参数辨识模型具体如图2所示。

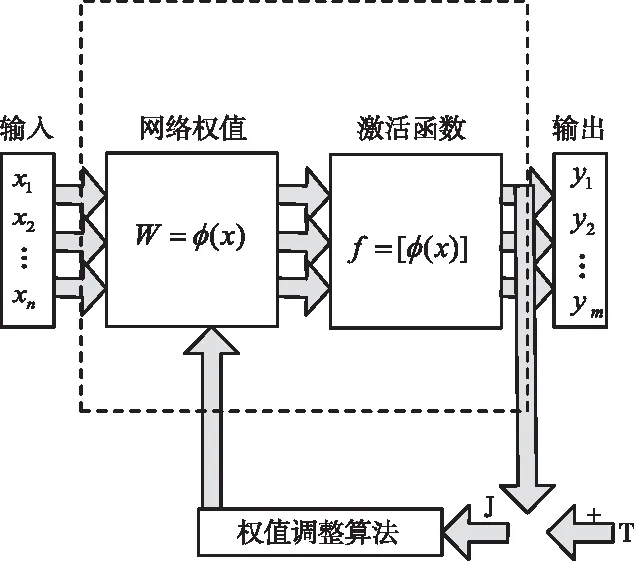
图2 参数辨识模型

2.4 权值调整

由于动力学系统存在输出误差，因此，需要对参数辨识模型的权值调整算法进行设置。动力学系统存在的输出误差可以用下式来表示：

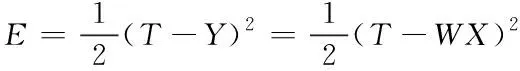
(12)

式(12)中，E表示动力学系统存在的输出误差；Y表示参数辨识模型输出矢量；W表示权值矩阵。

根据式(12)可知，动力学系统存在的输出误差最小值仅有一个，因此，通过梯度下降法对参数辨识模型的权值进行调整[11]。具体调整方法如下：

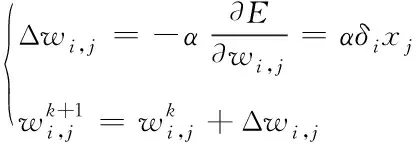
(13)

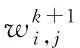
其中，α需要通过下式来确定：

(14)

2.5 参数辨识

利用参数辨识模型进行动力学系统的参数辨识，具体辨识步骤如下：

1)随机、均匀地取偏小的网络权值。

2)将输出、输入的实测数据组建成训练样本集。

3)在参数辨识模型的神经网络拓扑结构中输入训练样本，对输出Y进行计算。

4)对误差函数进行计算。

5)通过权值调整算法对权值进行调整。

6)对两次训练的前后权值误差进行计算，当计算结果小于给定误差，训练停止。并对训练次数进行比较，当训练次数比设定的终止次数大，训练停止，以避免由于权值不收敛带来异常结果[12]。

7)对训练网络取值进行转化，将其转化成动力学系统辨识参数。

3 仿真实验测试

3.1 实验动力学系统

在仿真实验中，利用基于调制函数法的动力学系统参数辨识算法对某伺服系统进行参数辨识，辨识的参数包括阻尼、刚度、惯性、死区四种物理参数。实验中的伺服系统是一个齿轮传动系统，由支撑结构、连接轴、负载、齿轮元件、电机构成，具体结构如图3所示。

图3 伺服系统具体结构

为了采集参数辨识数据，在负载端和电机端均对精度较高的编码器进行连接。实验伺服系统的参数具体如表1所示。

表1 实验伺服系统的参数

3.2 仿真方法

为满足仿真实验需要，搭建伺服系统仿真模型，将伺服系统仿真模型的姿态数据作为参数辨识模型神经网络拓扑结构的训练样本，具体如表2所示。

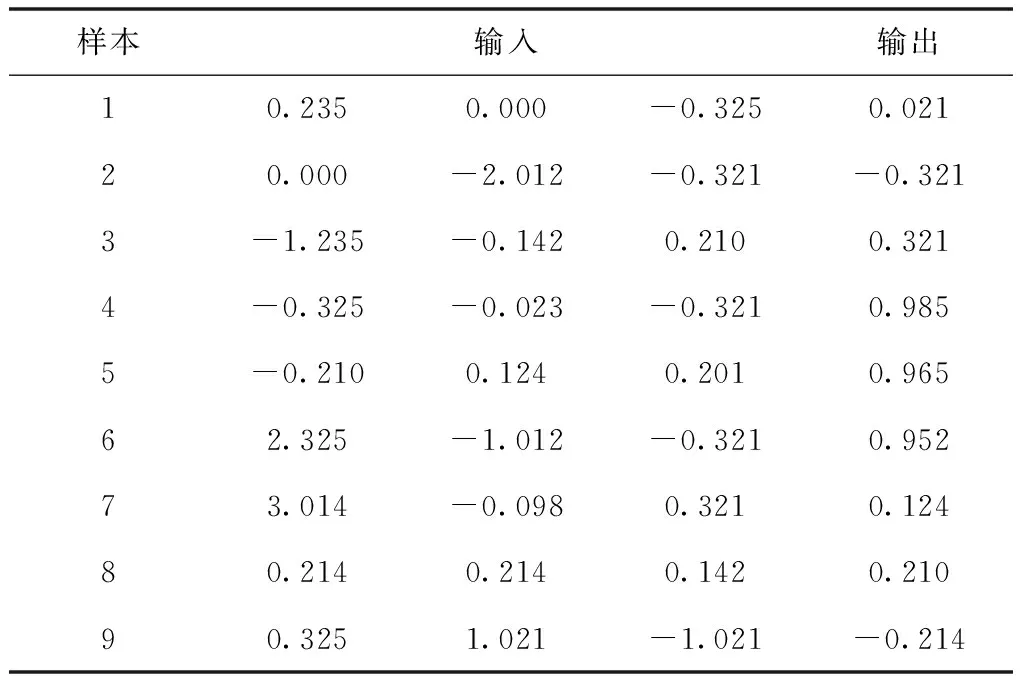
表2 训练样本

在利用设计算法对仿真模型进行参数辨识时，获取该方法的辨识精度数据、辨识速度数据。为使实验结果整体更加丰富、更具参考性，将现有的三种传统动力学系统参数辨识算法作为实验中的对比方法，进行对比实验。同样获取三种对比算法的辨识精度数据与辨识速度数据作为对比实验数据。这三种对比实验算法具体为基于等价准则、基于非线性定位、数值模拟下的动力学系统参数辨识算法。

3.3 实验数据分析

3.3.1 辨识精度实验数据分析

共辨识四种参数：阻尼、刚度、惯性、死区，测试基于调制函数法的动力学系统参数辨识算法与基于等价准则、基于非线性定位、数值模拟下的动力学系统参数辨识算法的参数辨识误差数据。四种参数的辨识误差实验数据具体如表3所示。

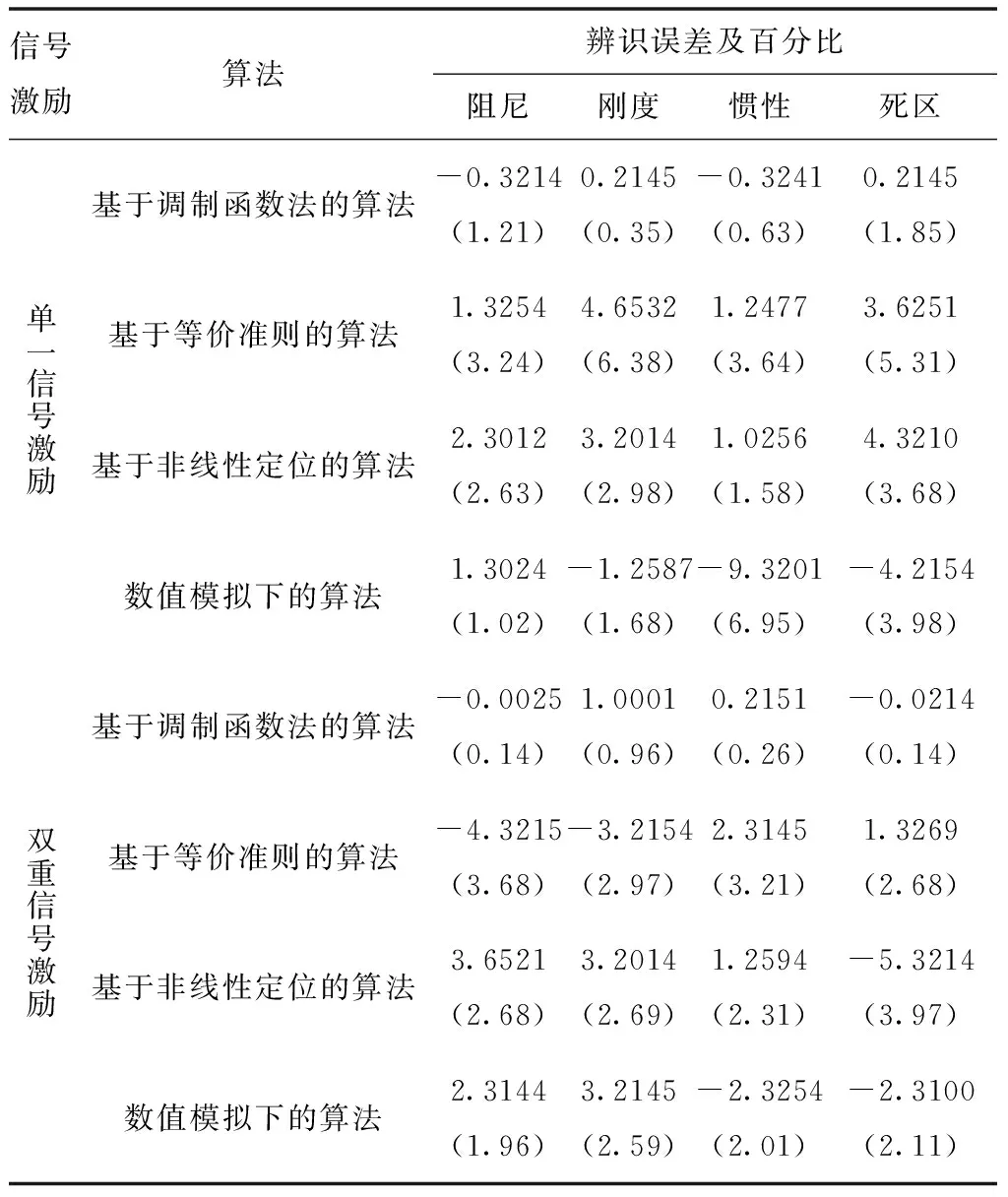
表3 四种参数的辨识误差实验数据

表3四种参数的辨识误差实验数据表明，对于阻尼、刚度、惯性、死区这四种参数，基于调制函数法的动力学系统参数辨识算法的辨识误差最低可达：0.14%、0.35%、0.26%、0.14%，整体辨识精度高于基于等价准则、基于非线性定位、数值模拟下的动力学系统参数辨识算法。

3.3.2 辨识速度实验数据分析

接着测试基于调制函数法的动力学系统参数辨识算法与基于等价准则、基于非线性定位、数值模拟下的动力学系统参数辨识算法的辨识时间，具体测试数据如表4所示。

表4 辨识时间具体测试数据

根据表4的辨识时间具体测试数据可知，设计算法的整体测试时间比数值模拟下、基于非线性定位、基于等价准则的动力学系统参数辨识算法低，说明该算法能够实现辨识时间的节约，提升参数辨识效率。

4 结束语

为了解决传统方法辨识精度与辨识速度较低的问题，提出基于调制函数法的动力学系统参数辨识算法。在对动力学系统参数辨识算法进行研究的过程中应用了调制函数法，实现了辨识误差的降低与辨识时间的缩短。在研究中发现该算法能够节省很大的计算消耗，是一种负担很轻的动力学系统参数辨识算法。