基于医疗行为的新型传染病传播模型仿真研究
黄 丽,叶春明
(1. 上海理工大学管理学院,上海 200093;2. 攀枝花学院智能制造学院,四川 攀枝花 617000)
1 引言
人类社会始终面临着新发传染病的严重威胁,据世界卫生组织统计,全球几乎每隔2-3年就会出现一种新型传染病。从2003年的非典SARS到2019年的新冠肺炎(COVID-19),新发传染病均对人类生命安全和社会经济生活造成了极大危害。根据2020年7月15日WHO公布的数据,爆发于2019年12月的新冠肺炎在全球的确诊病例超1300万,215个国家和地区均成为疫区,这已成为西班牙大流感以来全球最大规模的流行病,导致了1930年大萧条以来最大的经济停摆。
为应对新发、突发传染病重大疫情,建立疫情防控早期风险预测预警以及采取及时有效的应对措施是解决问题的关键。建立传染病传播模型,对预测传染病发展趋势和评估防疫措施等有基础作用[1]。经典的传染病数学模型有SIS模型,SIR模型和SEIR模型[2],随着研究的深入和新型传染病特征的出现,经典模型得到了系列扩展。文献[3]基于“病毒潜伏期”时滞特征和不同时段下的政府干预行为,提出了时变参数-SIR模型,分析了观测期内政府防控措施对疫情蔓延趋势的控制效果,并预测了疫情高峰的出现时间。文献[4]同时考虑了“病毒潜伏期”和“治疗周期”的时滞特征,以及政府干预行为,提出了时滞传染病动力学模型,预测了政府当前防疫力度对疫情发展趋势的影响。基于时滞传染病动力学模型,文献[5]结合中国疾控中心(CCDD)统计数据分布特征,建立了随机时滞传染病动力学模型,预测了疫情发展和峰值出现时间。为了实时预测疫情发展趋势,文献[6]将极限学习机与SIR模型结合,提出了一种新的极限IR预测模型,虽然对动力学模型进行了简化,但增强了模型的时变特性和实时预测功能。除此之外,还出现了其它一些预测模型,如分阶段非线性拟合的一般增长模型[7]。
用数学模型帮助预测传染病的发展趋势已成为共识[8],但针对现实的时变问题,数学建模的处理技术较为复杂。随着人工智能技术的发展,以元胞自动机等为代表的网络动力学模型又成了新的研究热点[9]。元胞自动机通过局部规则同步演化来反映整个系统的复杂变化,这与传染病的传播机制非常类似。由于规则调整灵活,仿真结果可视,元胞自动机特别适用于策略调整或改变的有效性研究。文献[10]以SARS为实例,用随机行走元胞自动机模拟人员移动对传染病疫情蔓延的影响,通过调整“移动比例”和“就医时间”规则,发现“限制人员移动”和“及时就医”能明显遏制疫情。文献[11]以甲型HIN1为实例,用元胞自动机模拟病毒在人群接触网络内的传播过程,通过调整“感染到治疗的间隔时长”,“疫苗注射比率”等规则,发现“及时就医”和适当的“疫苗注射比率”是控制传染病传播的有效防控策略。文献[12]以新冠肺炎为实例,通过元胞自动机将“积极防控”和“消极防控”规则下的感染人数做了可视化对比,从仿真角度证明了中国政府强有力的防控举措必要性。
尽管上述研究取得了不错的研究成果,但没有从传染病在医疗行为干预下的社群传播特征和演化规律视角,探索医疗资源有限下的医疗行为有效性,但这对政府应对未来新发传染病,增强社会防疫管控效力有着重要意义。
本文拟采用基于医疗行为变量的多态元胞自动机模型,以新冠病毒肺炎为例,试图在以下三方面进行创新和改进:一是模型的参数设定,尽量以官方报道或文献数据为依据,以期使研究结论更贴合实际;二是对医疗行为变量下的患者状态更加细分,以细化其在医疗行为变量下的病情发展;三是在演化规则上引入医疗行为变量“诊断”,“收治”和“疫苗注射”,研究其在“严防严控”和“复工复产”两种典型情景下对医疗资源需求和疫情控制的影响,同时通过“系统感染率”,“感染治愈率”和“医疗成本”来评估医疗行为在两种情景下的有效性。
2 新型传染病特征
新冠病毒(COVID-19)及其患者具有以下典型特征:①病毒的主要传播途径为“飞沫传播”和“接触传播”[13];②感染者患病状态多样性,患者的临床分型为“轻型、普通型、重型和危重型”,另外还有少量的无症状感染者;③存在多阶段时滞特征,即从“被感染”到“发病”阶段(潜伏期),从“发病”到“就诊”阶段,从“就诊”到“入院”阶段[13];④由于病毒超强传播力,几乎所有疫区都会经历“严格限制人员流动的联防联控”(简称“严防严控”)和“有限控制人员流动的复工复产”(简称“复工复产”)两个典型防控阶段。
3 基于医疗行为变量的多态元胞自动机模型
3.1 元胞自动机基本原理
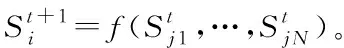
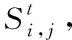

图1 二维元胞自动机Moore
3.2 建模假设
本文构建模型时提出以下基本假设:①研究区域内的人群总数保持不变,且人口呈均匀分布;②患者一旦被医院收治,则对外界易感人群不具有传染性;③患者如被确诊,但没有被医院收治,则对密切接触者仍有传染性,其传染强度减半;④基于发病期传染强度高于潜伏期传染强度[11],假定潜伏期患者和无症状感染者的传染强度相同,均低于发病期的传染强度;⑤考虑检测资源有限性和检测行为随机性,假定55%的患者会在“普通症”时接受检测,在“轻症”或“重症”时接受检测的患者分别约占35%和10%;⑥治愈患者获得免疫力,不会被再次感染。
3.3 元胞状态
元胞个体呈现多态性,表现为元胞在感染后在病情发展不同阶段接受“医疗检测”或“入院治疗”所呈现出的状态及其演化过程,如图2。
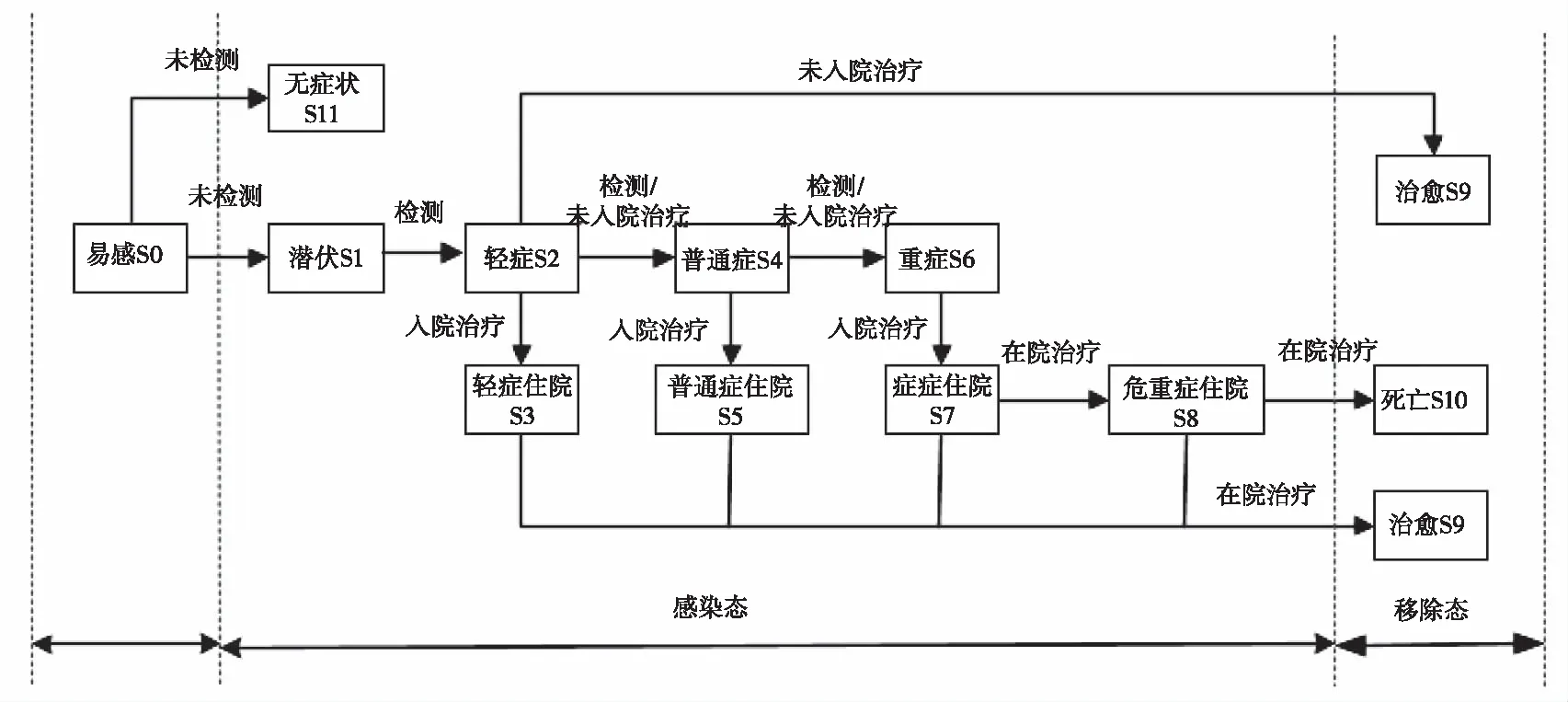
图2 不同时点医疗干预下的个体状态演化关系图元胞 在t时刻的状态和取值分别为:
1)易感态S0
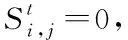
2)潜伏态S1,S11
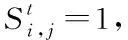
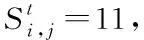
假定S1和S11既无症状,也未检测,都属于隐藏的传染者。
3)未入院治疗的发病态S2,S4,S6
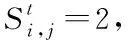
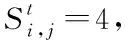
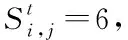
假定未入院治疗的发病个体S2,S4,S6,对外界均有传染力,但当“检测”确诊后,虽未入院但隔离增强,传染力减半;
4)入院治疗的发病态S3,S5,S7,S8
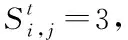
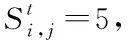
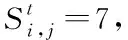

5)移除态S9,S10
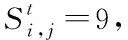
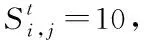
3.4 模型特性参数
通过免疫力参数,传染强度参数和时间参数来刻画传染病的传播特性。
1)免疫力参数
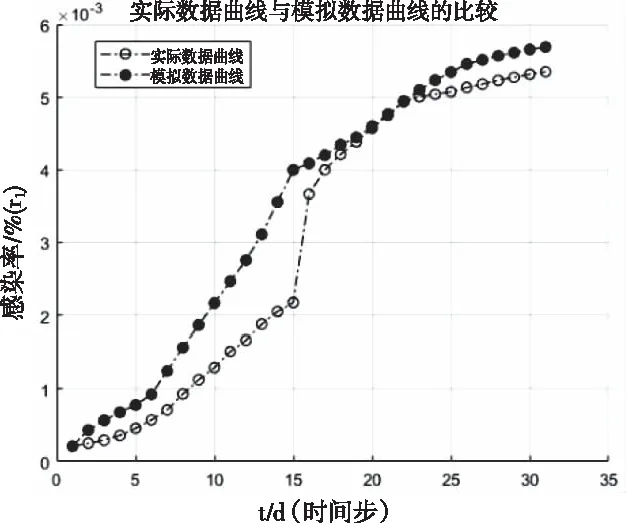
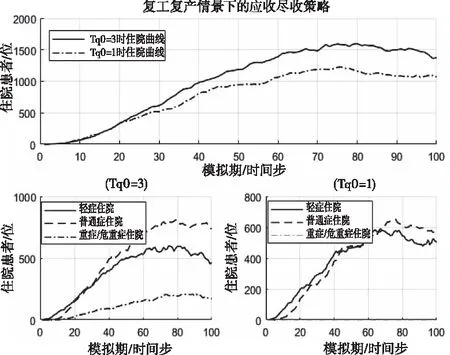
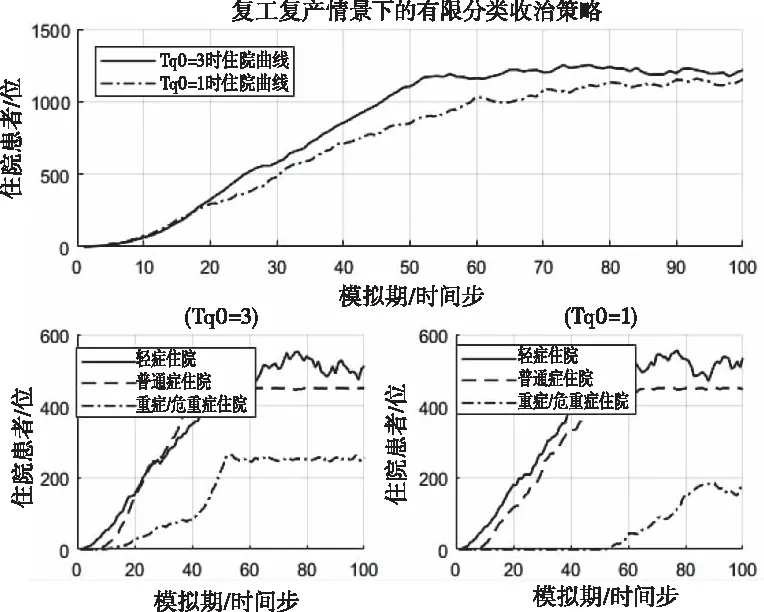
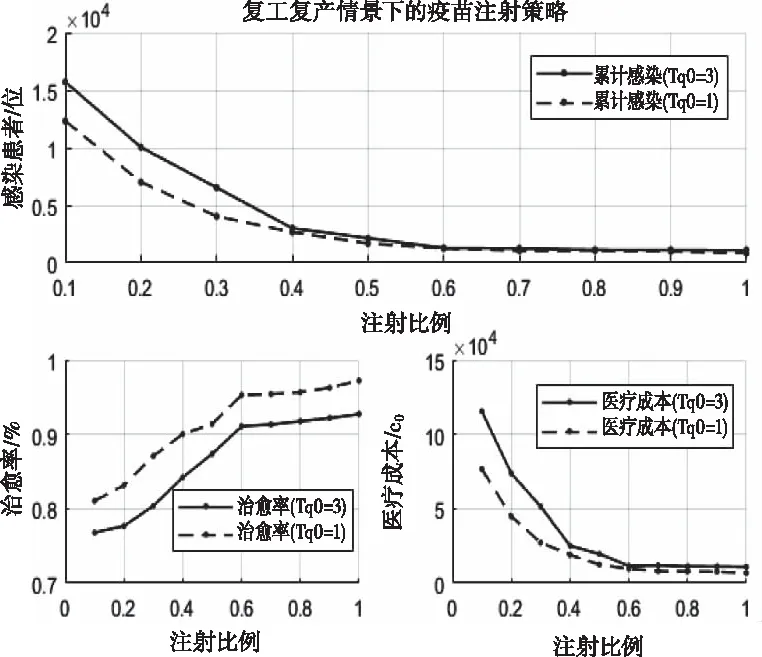
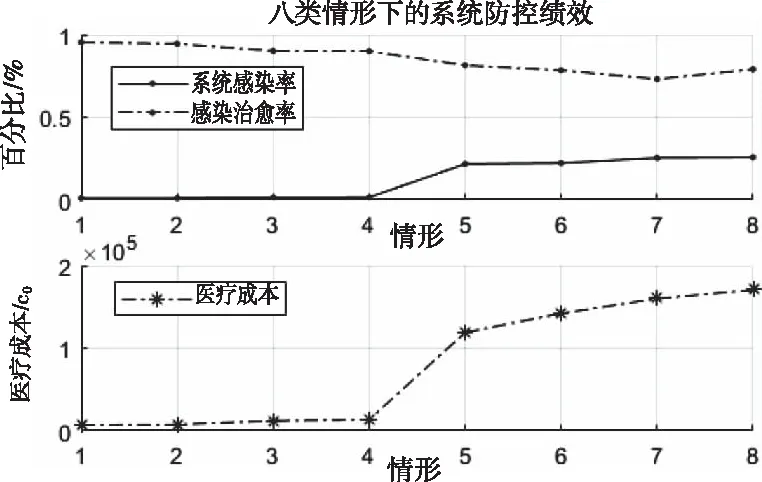
M1,易感态下的先天免疫力,0 M2,治愈后的免疫力,0 2)传染强度参数 I1,潜伏态下的传染强度,0 I2,发病态下的传染强度,0 3)时间参数 T1,平均潜伏时长,即从“被感染”到“发病”的平均时长; T2,平均轻症时长,即在未“入院治疗”中,“轻症”转“普通症”的平均时长; T3,平均普通症时长,即在未“入院治疗”中,“普通症”转“重症”的平均时长; T4,在院治疗中,“轻症”转“治愈”的平均时长; T5,在院治疗中,“普通症”转“治愈”的平均时长; T6,在院治疗中,“重症”转“治愈”的平均时长; T7,在院治疗中,“重症”转“危重症”的平均时长; T8,在院治疗中,“危重症”转“治愈”的平均时长; Tq,从发病到去医院检测的时长,Tq∈{Tq1,Tq2,Tq3},分别表示检测时状态为“轻症”,“普通症”,“重症”的检测时点; Tq0,从检测到确诊的时长; Tz,从确诊到入院的时长,Tz∈{Tz1,Tz2,Tz3},分别表示入院时为“轻症”,“普通症”,“重症”的入院等待时长。 4)概率参数 p0,无症状概率,当易感个体感染时,表现为无症状的概率为p0; p1,轻症在未入院治疗下的治愈概率; p2,在院治疗中,“重症”转“危重症”的概率; p3,死亡概率,在院治疗中,“危重症”以概率p3医治无效死亡。 (1) 由于几乎所有疫区都会经历“严防严控”和“复工复产”两个典型防控阶段,因此,考虑这两种典型情景下的医疗行为变量对疫情控制的影响。 1)两种典型情景下的移动性和隔离强度 情景Q1:严防严控 在此情景下,假定人们都被限制了随意移动,通常人们都只会和地理位置相邻的几个人接触;在元胞自动机模型里,中心元胞只会和邻胞有密切接触,即“接触式邻体传染”。 情景Q2:复工复产 在此情景下,假定人群的移动概率p和移动范围d均受到一定限制。每一次演化,假定未发病的个体只有50%的概率被允许做一次行走,即pm=0.5;由于人的活动范围有限,感染者更可能在距离自身较近的区域活动,因此采用非邻体高斯传染规则,选取一组取值,[σ=2,d=6],Pw=0.9887[15];其中σ表示方差,d表示移动范围,Pw表示活动范围内概率之和。因此,情景Q2的病毒传染规则是“接触式邻体传染”和“非邻体高斯传染”。 假定情景Q1的隔离强度高于Q2,其隔离强度值设置为:g1=5;g2=2。 2)医疗行为变量 医疗行为对传染病控制有重要影响,而医疗行为又受医疗资源的影响。这里研究的医疗行为主要有:a.诊断;b.收治;c.疫苗注射。 a.诊断变量 本文选取的诊断变量是Tq0,即医疗确诊时长“,取值为Tq0={1day, 3day}; b.收治变量 本文选取的收治变量主要体现为收治策略: 策略E1:应收尽收,即只要被确诊,就收治进医院进行隔离治疗;该策略的使用前提是假定医疗资源总是够用或无限; 策略E2:有限分类收治,即按照患者重症/危重症,普通症,轻症分类收治。假定轻症患者收治容量C21=N*0.01;普通症患者收治容量C22=N*0.005;重症/危重症患者收治容量C23=N*0.003;其中N表示研究区域人口总数。资源有限下的分类收治策略采用FCFS规则。 c.疫苗注射变量 本文选取的疫苗注射变量主要为疫苗注射比例R:0.1—1; 为评估两类典型情景下的医疗行为有效性,本文采用以下三个评估参数: 1)系统感染率r1 r1=Nr/N 其中,Nr表示模拟期结束时被感染的个体数,N表示模拟期总个体数; 2)感染治愈率r2 r2=Nz/Nr 其中,Nz表示模拟期结束时处于治愈状态的总个体数; 3)累计住院医疗成本Cg 以新冠病毒(COVID-19)引发的肺炎疫情为实例,对“严防严控”和“复工复产”两种典型情景下病毒在人群中传播过程进行模拟仿真,并在此基础上研究不同的医疗行为对医疗资源的需求和对病毒传播控制的影响。据文献报道,一项研究统计无症状感染者占总病例的0.04[16];患者平均潜伏时长5.2d[17],患者从发病到就诊平均时长:普通型5.9d,重型/危重型9.1d[18];患者住院平均时长:普通型11d,重型13d,危重型19d[19-20]。文献数据为模型参数设置提供了参考依据。 两种典型情景下的核心参数及控制变量设置见表1。 表1 两种典型情景下的模拟核心参数及控制变量 为验证模型有效性,选取2020年1月23日-2月22日[9]时段的武汉市,2020年1月23日武汉封城后,本地人口约有900万,基于平均潜伏时长,1月28日的确诊病例数可视为1月23日的感染病例数,即国家卫健委公布的1905例。这段时间的典型特征为“严防严控(情景Q1)”,具体表现从“封城”,“管制交通”到“封闭社区”等不断加强的隔离干预措施;采取的医疗措施有:①确诊时长由初期的3天以内缩短为中期的1天以内;②收治策略由初期的以收治重症/危重症为主调整成中期的“应收尽收”。 基于实例调研,模型元胞设置90000个,初始感染元胞设定为19例,基本实验参数不变,仿真时间设置31个时间步。隔离和医疗行为变量设置:①前15个时间步内,隔离强度g1=1.25;诊断时长Tq0=3,轻症患者不接收入院,普通症接收概率为0.3,重症/危重症接收概率1;②后16个时间步内,隔离强度g1=5;诊断时长Tq0=1,所有患者,一旦确诊,接收概率均为1。仿真运行30次,运用t-检验将2020年1月28日-2月27日实际公布的武汉确诊病例数和仿真的感染率做相关性分析,得相关性系数均值为0.975 031,说明模拟结果与实际公布数据接近,在一定程度上表明了模型的适用性。模拟感染率与实际感染率曲线见图3。 图3 实际数据与模拟数据的比较 在模型适用性基础上,展开“严防严控(Q1)”和“复工复产(Q2)”两种典型情景下几种重要医疗行为的效果分析。初始感染元胞设置为100例,仿真时间设置100步,基本实验参数不变。仿真运行30次。 在严防严控情景下,由于感染者数量得到了有效控制,医疗行为“诊断”和“收治”对医疗资源的需求均未达到系统上限,高峰持续时间短,能够在较短时间内控制住疫情。采用“应收尽收”策略或缩短诊断时长Tq0,均可进一步节省医疗资源。值得一提的是,从医疗资源的占用和释放速率来看,均是在短期内快速攀升(占用),达到顶峰后平缓下降(释放),在模拟期结束时控制在一个较低水平,见图4。 图4 Q1情景下患者住院曲线图 1)应收尽收策略分析 由于允许未发病人员在一定范围内移动,这对病毒传播的限制作用减弱。在医疗资源够用或无限前提下,采取“应收尽收”策略,住院患者数大幅增加,对医疗资源的最大需求量增加近10倍左右且高峰期持续时间长。在模拟期结束前,住院患者呈现出下降趋势,说明在“复工复产”情景下,大量充足的医疗资源投入能够在较长时间内控制住疫情。缩短诊断时长Tq0,可节省部分医疗资源,尤其是收治重症/危重症患者所需的高端医疗资源。Tq0的缩短在一定程度上抑制患者病情恶化,这对生命的保护和高端医疗资源需求的节省具有重要意义。值得一提的是,从医疗资源的占用速率来看,同样存在短期内快速攀升的现象,见图5。 图5 Q2情景E1策略下的住院曲线图 2)有效分类收治策略分析 采取“有效分类收治”策略,更符合医疗资源的有限性。在该策略下,住院患者从“快速增长”,到“缓慢增长”,直至“维持”在某一高位水平,这是由于随着患者数量的增加,某类医疗资源达到了容量上限而产生的瓶颈效应,使得医疗资源最高使用量的持续时间明显延长,截至模拟期结束,未见住院患者数有下降趋势。值得一提的是,在“复工复产”情景下,即使两种收治策略下的医疗资源最大使用量相差不大,但若受到医疗资源不足影响,医疗行为“诊断”和“收治”对疫情控制的有效性在较长时间内难见效果。截至模拟期结束,住院患者仍维持在高位水平,未出现下降趋势。在此情况下,诊断时长Tq0的缩短,对医疗资源的节省也非常有限,见图6。 图6 Q2情景E2策略下的住院曲线图 3)疫苗注射策略分析 如何在住院医疗资源有限约束下,有效开展复工复产,疫苗注射是传染病预防和控制的关键措施。假定在Q2情景E2策略下,易感群体的注射疫苗比例依次设置为0.1—1,见图7。 图7 Q2情景E2策略下的疫苗注射效果图 从图7看出,疫苗注射可以有效解决Q2情景E2策略出现的疫情控制难题。随着疫苗注射比例的增加,系统感染人数和医疗成本从显著减少到缓慢减少,治愈率从显著提升到缓慢提升,趋势线趋于平缓的转折点大约在0.6;即当注射比例达到60%时,系统的感染人数将维持在一个较低的水平,此时诊断时长Tq0的缩短对感染人数的减少和医疗成本的降低无明显效果,但对治愈率的提升仍然有效。 结合典型情景Q1和Q2,医院收治策略E1和E2,以及医疗诊断时长Tq0,共形成了8种情形,见表2。 表2 两类情景两类行为变量下的8种情形 这里的系统防控绩效主要表现为:①系统感染率r1;②感染治愈率r2;③住院医疗成本Cg。在8种情形中,前4种情形比后4种情形的防控绩效好,体现在较低的系统感染率,以及以较低的住院医疗成本获得较高的治愈率,说明了医疗行为“诊断”和“收治”在“严防严控”情景下的有效性。然而,相同的医疗行为组合在“复工复产”情景下,却表现出较差的防控绩效,不但所耗费的医疗成本急剧上升,而且系统感染率和感染治愈率均明显变差,可认为是行为失效的一种表现,见表2和图8。 对比表7和表8不难发现,在Q2情景E2策略下,当疫苗注射比例达到70%时,其系统防控绩效水平将得到大幅提升,相当于严防严控下的情形2。 图8 八类情形下的系统防控绩效 本文选取了“严防严控”和“复工复产”两个典型情景,基于新型传染病特征分析,构建了“诊断”,“收治”和“疫苗注射”三类医疗行为干预下的多态元胞自动机仿真模型,并通过新型冠状病毒实例验证了模型的适用性。研究发现,“严防严控”对阻断病毒传播起到了很强的隔离作用,使得医疗资源的需求量可控。缩短诊断时长和采用“应收尽收”策略均可进一步节省医疗资源。“复工复产”对医疗资源的需求量远大于“严防严控”,在疫情未得到有效控制前启动“复工复产”,可能会导致医疗资源不堪重负或面临疫情失控风险。 医疗行为“诊断”重在识别传染源,缩短诊断时长,不仅可以降低系统感染率,还可以减少患者向重症/危重症转化的概率;医疗行为“收治”重在隔离和救治感染者,“应收尽收”比“分类救治”能更早更快控制住疫情,但需要有充足的医疗资源保障;医疗行为“疫苗注射”重在保护易感人群,疫苗注射存在一个经济有效比例,值得去深入研究和探索。 最后,发现在疫情防控早期都会出现医疗资源需求在短期内快速攀升现象,这对医疗资源的应急配置与联合调度提出了较高的要求!从“严防严控”到“复工复产”,如何通过模型仿真推演将疫情防控阶段的转移风险降到最低,这将是下一步的研究重点和方向。3.5 模型演化规则
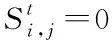
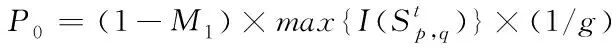
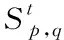
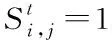
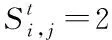
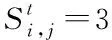
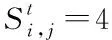
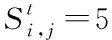
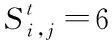
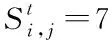

3.6 两种典型情景下的模型控制参数
3.7 模型评估参数
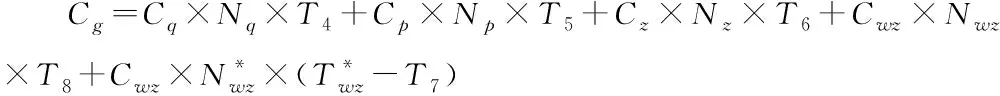
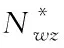
4 模型模拟与结果分析
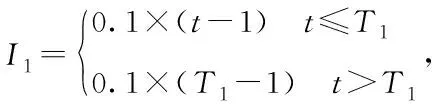

4.1 严防严控的情景分析
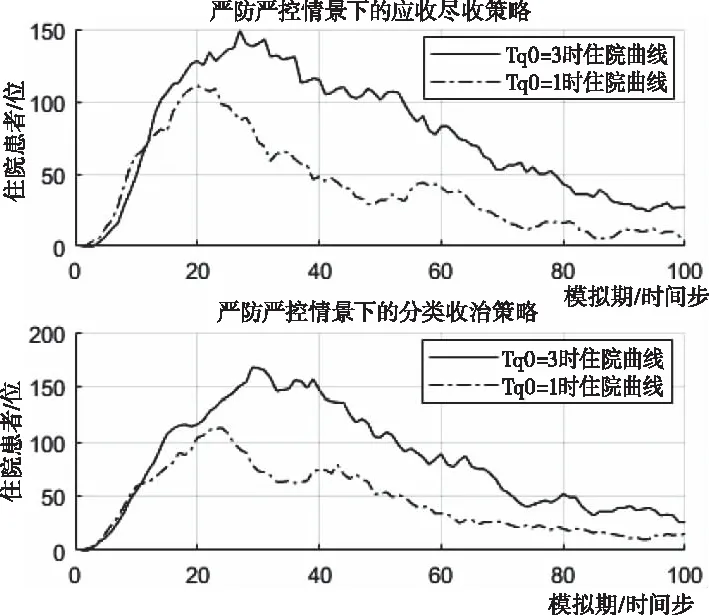
4.2 复工复产的情景分析
4.3 两类情景两类行为变量下的系统防控绩效

5 结论

