一种改进的卡尔曼目标实时检测与跟踪算法

邹航菲，罗婷婷

(1. 江西警察学院组织人事处，江西 南昌330103；2. 江西警察学院科研和发展规划处，江西 南昌330103)

1 引言

移动物体检测技术因其广泛的应用前景已成为当今世界一个重要的研究课题，在视频监控、视频索引、智能驾驶、智能机器人等领域发挥着重要作用，尤其是在模式识别和计算机视觉领域。从2015年至今，运动目标检测与跟踪发展迅速，一直以来不断有新的目标检测与跟踪算法被提出，例如Kalma算法、UPDT算法等，其中卡尔曼滤波算法就是一种功能强大的算法，它采用背景减法方法来检测视频中的运动物体，通过卡尔曼滤波器预测并估计物体的下一个状态，移动目标检测的定义是将移动目标与背景分离，获取目标的运动信息与位置，准确并实时标记运动目标。由于近年来检测前实施跟踪的思想被提出，国内外研究学者不断将跟踪与运动目标检测结合，来实现运动目标的检测与跟踪，目前比较流行的跟踪方法有粒子滤波器、动态规划法及机器学习算法等，以上方法都可以提高运动目标的跟踪能力，其中DSST、SAMF在应用中取得了良好的性能。

目标跟踪算法的改进主要从来两个方面来实施：①基于网络的改进，例如：SimRPN++算法、DLT算法等；②结合相关滤波器，包括ECO算法、C-COT算法等。但是在复杂环境条件下进行运动目标跟踪时，为了提升跟踪的稳定性，面临着许多挑战，诸如：形态变化、速度变化、尺度变化、图像模糊等等，这时通过将滤波算法与跟踪算法结合不断被研究者研究与尝试，例如有学者将KCF算法与C-COT算法结合对运动进行跟踪，提高了目标跟踪的准确性与鲁棒性[4]。

本文基于Kalman算法，提出一种在卡尔曼算法框架下结合粒子滤波器的优化方法，将检测前实施跟踪的思想引入其中，用于解决卡尔曼滤波算法在运动目标跟踪上不足的问题，满足检测精度更高、实时性更强、跟踪效果更好的需求，提升运动目标跟踪的稳定性。

2 标准Kalman滤波器检测原理

Kalman滤波器其实是一组数学方程，它通过最小化平方误差均值的方式，实现一种有效的计算递归方法来估计运动目标的状态。卡尔曼滤波器的方程可以分为两组：预测方程和校正方程：

①预测方程负责提前预测当前状态估计

(1)

(2)

②校正方程负责调整预测估计

(3)

(4)

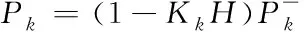
(5)

卡尔曼滤波器包含预测和修正两个部分覆盖高级操作的不同部分，一个标准的卡尔曼滤波器周期循环如图1所示。

图1 标准Kalman滤波算法循环

3 Kalman滤波算法与粒子滤波器相结合

卡尔曼滤波算法是基于预测进行运动目标检测与跟踪，跟踪效果差，实时性效果不能满足需求。将专门用于目标跟踪的粒子滤波器方法引入到卡尔曼滤波算法中，使粒子滤波器的跟踪效果传递给卡尔曼滤波算法，这样不仅实现了检测前实施跟踪的思想，而且达到了检测精度更高、实时性更强、跟踪效果更好的运动目标检测跟踪需求。卡尔曼滤波算法与粒子滤波器相结合的流程图如图2所示。

图2 卡尔曼滤波算法与粒子滤波器相结合流程图

卡尔曼滤波算法与粒子滤波器相结合的算法步骤：

①预测：第K帧目标位置在卡尔曼滤滤波算法公式进行计算，预测出第K+1帧运动目标的期望位置。

②目标跟踪定位：将步骤①中的预测位置导入到粒子滤波器中，在K+1帧期望位置进行搜索迭代，计算得到运动目标的真实位置。

③修正：根据步骤②中粒子滤波器计算得到的运动目标真实位置，Kalman滤波算法进行位置修正，更新运动目标位置状态。

④循环：不断循环步骤①②③，进行“预测-目标跟踪-目标修正”，完成运动目标实时检测与跟踪。

优化算法实现运动目标检测与跟踪的具体过程如图3所示。

图3 优化算法目标跟踪实现过程

除此之外，本文借鉴了分类树的原理方法，利用树形结构尺度自适应原理分别对运动目标的位置和尺度进行粒子滤波，具体实施过程分为两步：1)通过位置粒子滤波器的计算，确定运动目标的位置中心；2)在步骤1)的基础上进行树形尺度估计，精确定位运动目标位置。其原理示意图如图4所示。

图4 树形结构跟踪原理图

4 计算机仿真与分析

为了验证Kalman滤波算法与粒子滤波器结合后运动目标检测与跟踪的性能，本文进行了对比实验，分别对单纯的Kalman滤波和改进的算法在不同的应用场景下进行运动目标检测与跟踪。

4.1 单纯Kalman滤波算法

第一组实验只采用单纯的Kalman滤波算法，场景一在固定复杂背景下以人为运动目标的情况下进行运动检测跟踪，检测跟踪结果如图5所示，实验图像大小为364×289，整个图像共243帧，选取结果视频中的50帧、95帧、136帧、181帧、200帧、239帧作实验结果比较。

图5 场景一下Kalman算法效果图

场景二在运动背景下以运动的足球作为运动目标进行运动目标检测跟踪，检测跟踪结果如图6所示，实验图像大小为636×350，整个图像共346帧，选取结果视频中的46帧、100帧、147帧、253帧、298帧、326帧作实验结果比较。

图6 场景二下Kalman算法效果图

4.2 Kalman与粒子滤波器结合

为了验证改进算法的运动目标检测跟踪效果，分别对场景一和场景二进行仿真，如图7和图8所示，所有的实验参数与帧数选择与4.1中一致。

图7 场景一下Kalman+粒子滤波器结果图

图8 场景二下Kalman+粒子滤波器效果图

4.3 结果分析

从实验中运动目标检测跟踪的效果来看，Kalman与粒子滤波器结合算法在两种不同的环境及运动目标的情况下，不仅具有更高的检测精度，而且具有更好的实时性跟踪效果，克服了运动目标不断改变运动轨迹引起的跟踪失败问题，不论是在复杂背景还是动态背景下都能够实现准确跟踪。

通过对在场景一和场景二下不同算法目标跟踪准确率进行统计，得出如图9所示的运动目标检测跟踪准确率对比图。

图9 不同场景下跟踪准确率对比图

从图9中可以看出，在两种不同场景下单纯使用Kalman滤波算法的跟踪准确率分别为88%和89%，运动目标跟踪准确率较低，而经过结合粒子滤波器之后的改进算法跟踪准确率分别为98%和96%，两种场景下跟踪准确率得到明显提升。

为了验证改进算法的其它性能，本文分别对迭代次数、算法耗时进行了统计计算，每组对比实验共进行30次，分别计算出两种算法的平均迭代次数和平均算法耗时，具体数据如表1所示。

表1 两种算法性能对比图

从表1中可以看出，由于改进算法具有更好的跟踪效果，所以在迭代次数上会有所增加，但是在算法耗时上却比单纯的Kalman有所减少，这也证明了粒子滤波器的优越性，同时验证了改进算法具有更高的性能，可行有效。

5 结论

本文利用Kalman滤波算法与粒子滤波器的结合实现运动目标的检测与跟踪。该算法将粒子滤波器的跟踪方法引入到Kalman滤波算法当中，通过将Kalman预测的位置信息导入到粒子滤波器中，在K+1帧期望位置进行搜索迭代，计算得到运动目标的真实位置，实现实时跟踪。从仿真可知，改进后的算法较好的解决了Kalman滤波算法在目标实时跟踪上不足的问题，在不同应用场景下目标跟踪准确率都得到明显提升，且性能也具有优越性，更具稳定性。结果表明，本文提出的改进算法在视频监控等领域中的运动目标检测与跟踪具有显著意义。