NURBS及其偏移曲线的插补方法

马虎亮，王燕青，杨胜强，吕明

（太原理工大学 机械与运载工程学院, 太原 030024）

NURBS（非均匀有理B样条）曲线目前作为自由曲线的通用表达方式，由于其灵活性、易操作性等优点被广泛应用在机械设计领域[1]。NURBS曲线相对于一般直线、圆弧等常用曲线和Bezier、B样条等控制曲线相对复杂，计算效率不高。因此，NURBS曲线的插补计算也成为机械加工领域的重点和难点之一。

NURBS曲线的插补计算主要有3种方法：使用递推公式的直接计算法、矩阵法和De-Boor算法。学者们从不同的角度进行了研究：文献[2-4]分别引入Newton-Rapson、Runge-Kutta和牛顿迭代法来计算下一步的插补点；孔祥宏等[5]利用递推公式的显示方程改进计算过程；冯高杰等[6]用分段插补来调节加减速的自适应插补算法；王国勋等[7]提出了基于矩阵法的插补点快速求导方法。上述方法中NURBS曲线求解插补点的过程相对于一般曲线来说还是过于复杂，求取参数较多，计算量较大，并且对于样条曲线的刀补轨迹计算没有深入分析。

当前对于NURBS曲线的加工主要采用周期采样法,通过上位机粗插补和下位机精插补的结合提高加工精度，上位机根据采用周期采集曲线上的点。文献[8-11]研究了NURBS曲线插补中上位机实现加减速控制的方法。这些方法使用曲线上的点的数量较少，总的计算量不大，具有很高的速度控制功能，但精度较低，不适用与对精度要求高的场合。文献[12-15]是学者们采用插补或者补偿等方法对于不同应用场合减小误差所做的探索。

本文提出的参数跟踪法是一种通用曲线插补方法，应用在NURBS曲线的插补计算中，可以在保证精度的前提下减少计算量。首先介绍了参数跟踪法的基本原理，然后将其应用到NURBS曲线的插补计算中，随后将其扩展到曲线的刀具补偿和处理过程，最后研究了NURBS曲线的坐标补偿方法。

1 参数跟踪法的基本原理和计算过程

参数跟踪法以曲线的参数方程为研究对象，首先确定各个轴的参数表达式并进行归一化处理，使参数u的取值范围限制在[0，1]，然后以曲线的导矢为依据，对下一步的插补点进行计算，得到下一步插补点的坐标和当前步的插补结果，最后循环计算至终点。参数跟踪法得到的结果属于脉冲增量式，即单步插补结果是各个轴单步运动，插补精度高。

1.1 参数跟踪法的方程

参数跟踪法首先用到曲线的参数方程，表达式为

式中u为曲线的参数，u∈[0,1]。

对于参数范围不在[0，1]的参数曲线，需要对其参数值进行归一化，并且对参数方程进行调整。

在计算下一个插补点时，需要使用曲线的参数微分方程，即

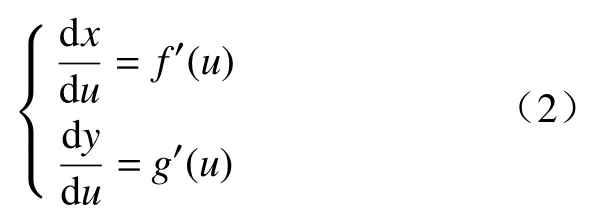
1.2 下一个插补点的计算

所有针对NURBS曲线的插补计算都是参数u从0到1的过程，每步插补计算参数的增加值称为跨步步长 Δu。不同的插补方法计算得到的跨步步长不同。根据二阶泰勒公式曲线任意点的坐标计算公式为

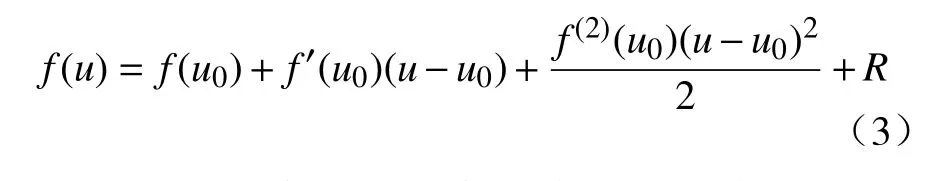
式中u0为对应参考点的参数值。在脉冲增量式的插补运算中，各轴的单个脉冲增量为 Δl，因此取Δl=f(u)−f(u0)； Δl的取值通常可以达到 0.1 ~ 1 μm，这样导致 Δu=u−u0，因此略去高阶导数，只使用一次项，得到

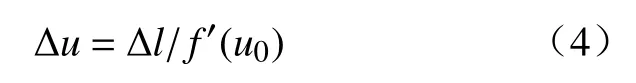
把各轴的微分方程代入式（4）计算可以得到各个轴的跨步步长，但由于各个轴的导数不同，因此各轴对应的 Δu也不同，这里取多个 Δu的最小值为跨步步长。再根据u=u0+Δu得到下一个插补点的参数值并可以计算各轴坐标值。

1.3 插补过程

参数跟踪法的运算流程如图1所示。

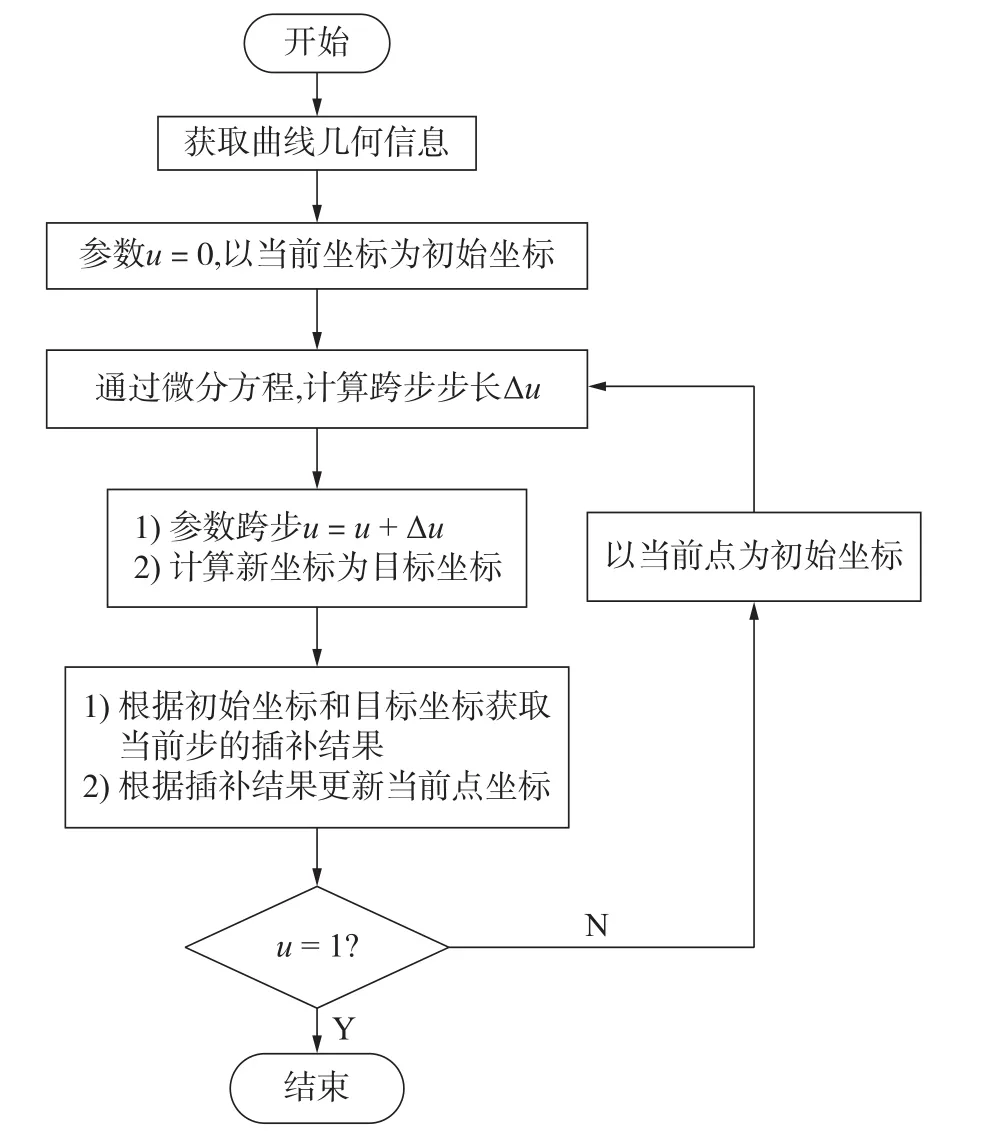
图1 参数跟踪法的运算流程

参数跟踪法的运算流程具体步骤如下：

步骤1 参数跟踪法在获取到曲线几何信息后，设置初始参数u=0，初始点坐标Q(xs,ys)。

步骤2 根据曲线参数微分方程式（4）求出各轴关于参数的导数，按照式（4）计算出各轴参数差值取最小值为跨步步长 Δu，更新参数值u=(u0+Δu)。计算新点的坐标Q(xm,ym)，然后根据新旧坐标的差值ΔQ(Δx,Δy)得到插补结果。插补结果多为单步和双步。

步骤3 循环步骤2 ，直到u=1，曲线到达终点。

由于每次获取插补结果都是以参数值对应点的坐标为目标，故名其为参数跟踪法。参数跟踪法每次插补目标都为曲线上的值，完成插补后的坐标误差都在单步之内。计算过程简单，只需要使用参数方程及其一阶导数。

2 NURBS 曲线的参数跟踪法计算

NURBS曲线的表达式符合参数跟踪法的计算要求，并且参数范围是[0，1]，不需要进行归一化处理。参数跟踪法可以用于NURBS曲线的插补计算。

2.1 NURBS曲线的计算基础

参数跟踪法的插补过程需要计算曲线上的点和导矢。NURBS曲线上点的表达式为

式中：wi为权因子；Pi为曲线的控制点；Ni,k(u)为与u相关的基函数。从式（5）来看，分子A(u)可以等同加权控制点wiPi的B样条曲线表达式，分母W(u)可以等同为权因子wi的B样条表达式。因此，NURBS曲线的计算可以转换为加权控制点的计算结果除以权因子的B样条函数计算结果。使用De-Boor算法可以快速计算B样条曲线上的点。

NURBS曲线上各点的导矢计算式为

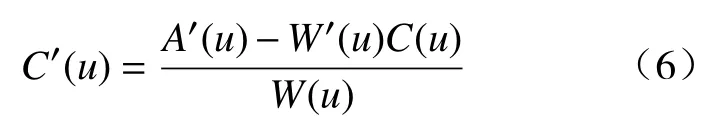
式中：A′(u) 为A(u)的的导数，即加权控制点wiPi的B样条函数导数；W′(u) 为W(u)的导数，即权因子wi的B样条函数导数。

式（6）是由式（5）对参数u进行求导所得，C(u)和W(u)在式（5）中已算出。

根据B样条曲线的性质，p次B样条曲线的导矢等于p−1次B样条曲线，其控制点表达式为

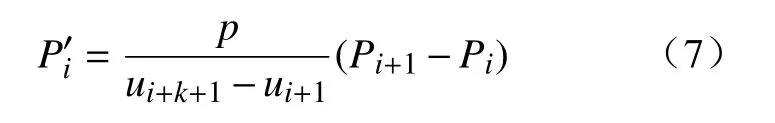
式中ui为对应的节点向量。将加权控制点wiPi和权因子wi代入可求得p−1次B样条曲线的控制点，再对节点向量进行对应处理即可计算得到A′(u)和W′(u)，最后根据式（6）得到 NURBS 曲线的任意点的导矢值。

2.2 参数跟踪法计算NURBS曲线实例

以NURBS曲线实例来说明NURBS的参数跟踪插补方法的计算过程。三次NURBS曲线的控制点和权因子如表1 所示。节点向量V=[0, 0, 0, 0,0.143, 0.286, 0.429, 0.571, 0.714, 0.857, 1, 1, 1, 1]，单个脉冲增量为 1 μm。

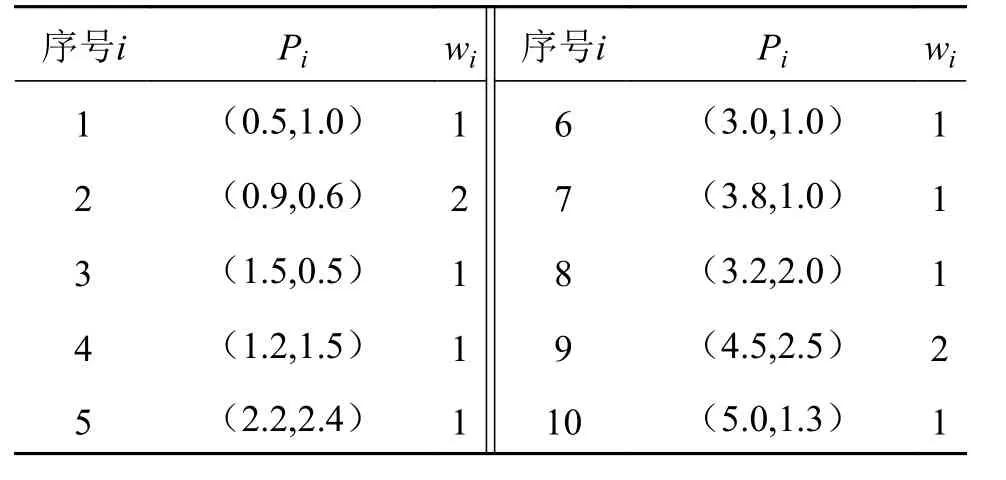
表1 NURBS 曲线控制点和权因子

NURBS曲线的插补计算过程：

步骤1 设定P1(0.5,1.0)为初始点，且u=0；

步骤2 根据式（7）计算当前点的导矢，得到dx/du和 dy/du的值，令 dx=dy=0.001 mm，计算X轴和Y轴对应的du，取较小值为跨步步长 Δu。然后更新参数u的值，根据式（6）计算当前点坐标，最后根据当前点坐标得到当前步的插补结果。

步骤3 判断u是否等于1，等于1结束，小于1循环步骤2。

插补结果共6402步，插补结果如图2a）中所示，图2b）为插补结果的局部放大图。从图中可以看出，插补结果精度高，没有累积误差。

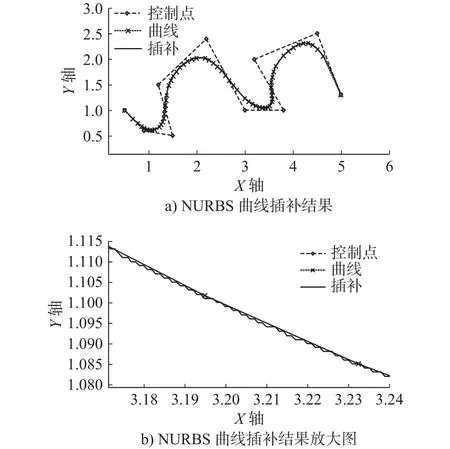
图2 NURBS 曲线插补结果

3 恒定刀具补偿的插补计算

数控加工中NURBS曲线的获得方式有两种方式，一种是在机械设计中直接使用NURBS曲线进行的设计，另外一种是通过测量曲面，然后使用NURBS曲线进行拟合得到的结果。两种方式得到的数据信息都包含了控制点、节点矢量和权因子，但都是属于加工前的轨迹信息，在实际加工中需要转换为加工轨迹。通常在加工中使用固定刀具加工NURBS曲线，因此加工轨迹与结果曲线相差一个刀具半径。

3.1 恒定刀具补偿的计算过程

曲线具有凹凸性，其刀具补偿为曲线各点沿法线方向偏移后的轨迹。根据补偿方向可分为左刀补和右刀补。NURBS曲线为参数表达式，因此曲线导矢方向与法线方向垂直，由于参数跟踪插补方法中包含了对导矢的求值，因此利用导矢求解左右刀补后的位置。如图3所示，根据参数微分方程可以求解曲线上点M的导矢(x′,y′)。左刀补为导矢方向逆时针旋转90°，右刀补为导矢方向顺时针旋转90°。计算时相应的XY轴分量进行旋转即可。

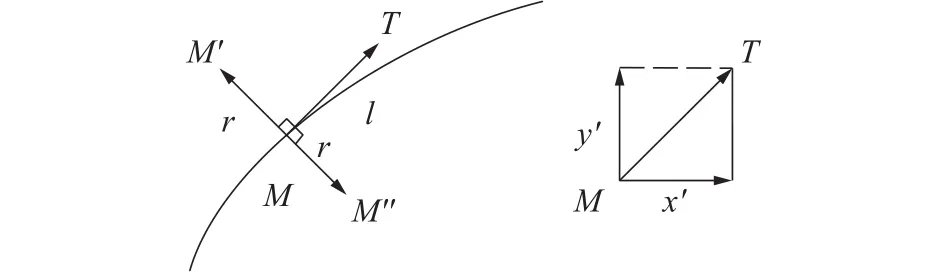
图3 导矢与刀补关系图

曲线上对应点的刀具中心位置计算公式为

式中：r为刀具补偿值；x′、y′ 为曲线当前点的导矢分量；l为导矢长度值，为符号，左刀补时取上方符号，右刀补时取下方符号。

3.2 插补结果后处理

刀具轨迹是曲线偏移后的结果，由于曲线的凹凸性，使其偏移曲线的长度有所增减。偏向凸的一侧曲线长度增加，数据点增多；偏向凹的一侧曲线长度减少，数据点减少。这是偏移曲线的特点之一。

直线、圆弧和圆锥曲线等几何元素在偏移时只考虑单个凹凸性。NURBS曲线由于其灵活性，可将多种曲线的特征包含在一条曲线中，因此其偏移后的轨迹可能既包含凹曲线也包含凸曲线的偏移结果。NURBS曲线偏移量较小时点不会重合，但偏移量如果过大时，偏移线会出现重合和交叉，这就是曲线偏移的自相交现象，应用在加工中导致发生过切。曲线自相交现象如图4a）和图4b）所示。

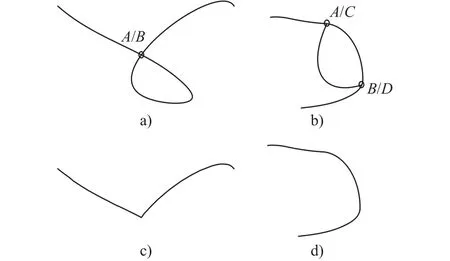
图4 偏移曲线的“打结”现象

处理NURBS曲线偏移的数学方法比较复杂，需要重新取型值点再反算控制点，计算过程复杂，而且在打结处，通常处理方式是打断曲线从而生成多个曲线。

本文提供了一种处理偏移曲线出现自相交现象的面向插补结果的处理办法——坐标消结法。坐标消结法是利用了插补结果具有确定精度坐标的特性：凡是打结必然会有重合点。坐标消结法利用包含了坐标值的插补结果，首先遍历插补点得到相同坐标的序号集合，然后对序号集合进行合并处理，最后在插补结果中去除打结段。

图4a）为最常见的交点情况，曲线只有一个交点的情况处理比较简单，记录A点和B点的序号去掉中间段即可。图4b）中重复点为一段曲线，点的序号从前到后一次为A→B→C→D，A和C共点、B和D共点，去除时需要保留AB段。图4c）和图4d）是去除自相交部分的曲线。

图5中补偿曲线是原有NURBS曲线使用3.1节的方法偏移0.3 mm后的插补结果，显示其中有两处自相交。在遍历插补点后得到的相同坐标的序号集合数量为16组，如表2中所示，需要对其进行合并处理。使用坐标消除法对插补结果处理后，需要消除的两段为 3 90→565和 3 634→4185共728步。插补结果步数从7218步减少到6490步。处理后结果如图5中处理曲线所示，去除掉偏移曲线的两个结，加工中不会产生过切现象。图5中所示处理曲线为便于观察纵坐标上移1 mm，可以看到坐标消结法去除了偏移曲线的交叉部分。

表2 插补结果中相同坐标点集合

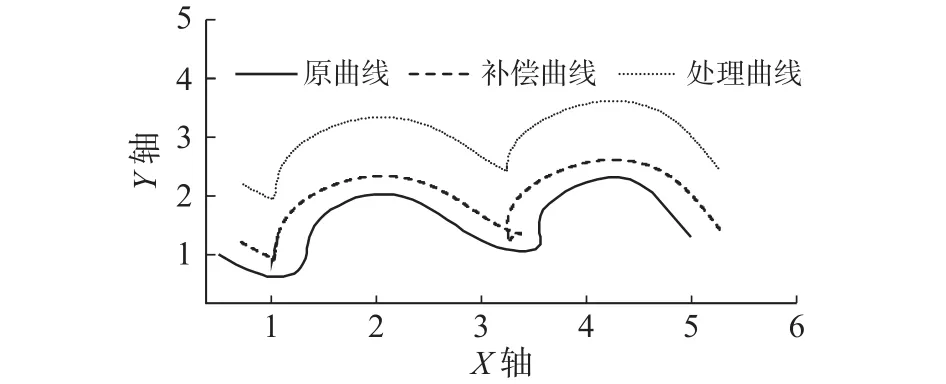
图5 NURBS 刀具补偿插补结果后处理

4 线性刀具补偿插补计算

恒定刀具补偿一般应用在铣削等加工刀具磨损量很小的场合。在电火花加工中电极随着加工时间是有损耗的，而且加工某些材料损时电极损耗量是非常可观的，此时就需要对电极进行补偿。由于电极损耗量在相同加工条件下是固定的，因此可以将补偿随加工时间进行线性变换。线性补偿的计算公式为

式中：r0为固定刀具补偿值，mm；k为电极补偿系数，mm/步；n为加工步数；r为刀具补偿值，mm。

由于插补过程是按照周期内步数来进行衡量的，因此电极的补偿系数需要转换成与步数相关。将式（8）中的补偿半径用式（9）计算，即可得到变补偿的曲线插补结果。取k=−0.000 04 mm/步，通过计算得到的插补结果如图6所示。曲线插补从左侧开始补偿值为0.3 mm，到右侧结束时根据式（9）计算变为0.04 mm，工具电极损耗得到补偿。

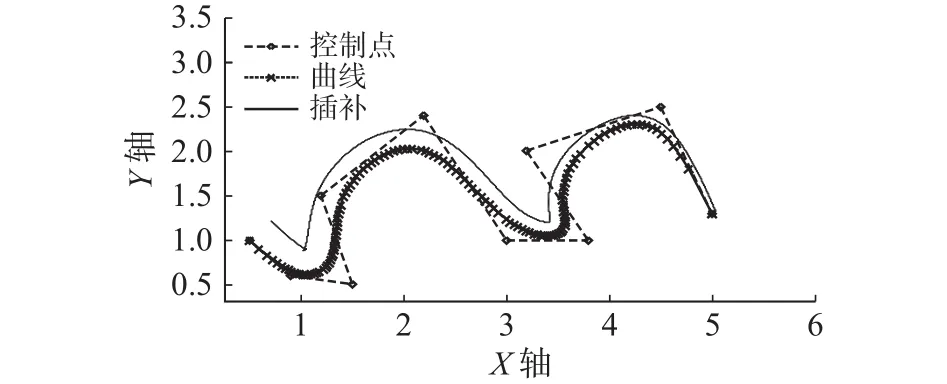
图6 NURBS 曲线线性补偿图

5 坐标补偿插补计算

在加工过程中，由于机床和刀具由于移动和受力等原因会在加工中产生振动，导致加工NURBS曲线时出现周期性或非周期性的坐标漂移现象，这是由于加工运动产生的坐标误差。坐标误差最终会反应加工后的曲线上，这种误差可以通过三坐标测量仪等轮廓测量装置测量。

坐标误差可以通过坐标补偿技术进行消减。具体办法是通过试加工得到曲线，再通过测量轮廓和目标曲线进行比较得到坐标误差表。再对坐标误差表进行多项式拟合，将拟合后的坐标公式与NURBS曲线的插补点坐标相加来消除坐标误差。

如图7所示，实际曲线表示加工后的曲线，与目标曲线有坐标误差，误差值拟合曲线为式（10），是一条4次多项式曲线。在计算出NURBS曲线x坐标后，可以通过式（10）计算出坐标误差的y坐标值，与曲线的y坐标值相加，最后再进行刀具补偿。机补曲线是实际曲线经过坐标补偿得到的曲线，与目标曲线重合。刀补曲线是机补曲线的刀具补偿插补结果。

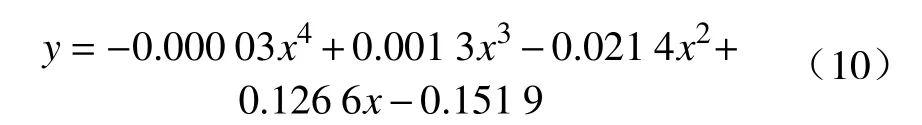
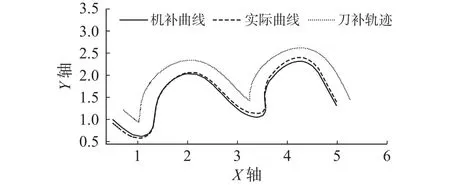
图7 坐标补偿与刀补轨迹

6 结论

参数跟踪法可以简洁有效地对NURBS及其偏移曲线进行插补。NURBS曲线在加工中出现的误差也可以利用多种补偿方法进行消除,从而提高NURBS曲线的加工精度。参数跟踪法对于NURBS曲线的计算方法可以扩展到其他类型的参数曲线，具有简化插补计算和提高插补效率的作用。