不同工质和蓄热介质下AA-CAES三联产系统特性研究
李 鹏,胡庆亚,韩中合
(1.华北电力大学 能源动力与机械工程学院,河北保定 071003;2.华北电力大学 河北省低碳高效发电技术重点实验室,河北保定 071003)
风能、太阳能和潮汐能等可再生能源已成为许多国家发展不可或缺的能源[1]。然而,可再生能源的波动性会对电网并网造成冲击[1-2]。电能储存技术和电气系统的集成是解决可靠性问题的重要方案之一[3]。其中,先进绝热压缩空气储能(AA-CAES)系统将压缩空气储能(CAES)系统与储热(TES)系统集成,不仅使并网过程更加可靠,还实现了化石燃料的零消耗和污染物的零排放[4-5]。
近年来,研究人员针对AA-CAES的建模仿真、核心部件分析、参数分析和可再生能源耦合等方面进行了深入研究。Mozayeni等[1]建立了AA-CAES系统的热力学模型,该模型主要包括压缩机、膨胀机、TES系统和储气设备。也有研究人员对AA-CAES系统进行了仿真分析,并研究了系统效率与核心部件之间的关系。He等[6]研究发现,通过匹配压缩机叶片进口角可以减小攻角损失,进而提升系统效率。Kushnir等[7]发现储气室壁面的传热对空气的温度和压力变化有很大影响。李雪梅等[8]发现压缩机级数相同时,膨胀机级数越多,单位质量空气释放的膨胀功越多。Yang等[9]发现换热器的压力损失越大,相应的系统储能效率越低。Jubeh等[10-11]研究了环境温度、最大压比、空气质量流量、压缩机和膨胀机效率在内的关键参数对系统效率的影响,结果表明环境温度和最大压比越低,空气质量流量、压缩机和膨胀机效率越高,系统的储能效率越高。Mohammadi等[12-16]分别分析了太阳能、风能、飞轮储能和抽水蓄能耦合到AA-CAES的系统特性,结果表明与传统AA-CAES系统相比,耦合可再生能源的系统能够产生更多的膨胀功,其储能效率及效率显著提高。
在实际生活中,需要满足用户对供电、供暖和制冷的多元化能源需求,因此He等[17-19]致力于将AA-CAES系统改造为冷热电三联产系统,并评估了其热力学性能。结果表明,与纯供电系统相比,冷热电三联产系统在满足电负荷的同时可提供可观的供热量和制冷量,使系统的储能密度和储能效率更高;另外,改变压缩机和膨胀机的运行方式及蓄热系统的热量分配比,也可以灵活应对系统负荷变化。
以上研究在对AA-CAES及其耦合系统的设计和优化过程中,忽略了不同工质和蓄热介质本身的热物性对换热器及整个系统的影响,只将换热器效能设定为定值。针对这一不足,笔者在上述文献的基础上建立基于AA-CAES的冷热电三联产系统,提出采用不同工质和蓄热介质的4种组合方案。在基本设计参数下,对系统进行能量分析和分析;并通过改变低温蓄热介质温度和对流传热系数,分析其对4种组合方案的系统性能的影响;同时以效率和储能密度作为目标函数,对系统进行多目标优化。研究结果为系统的工质和蓄热介质的选取提供了参考。
1 模型建立
1.1 系统概述
基于AA-CAES的三联产系统工作原理图如图1所示。该系统主要分为储能子系统和释能子系统2个子系统。其中,储能子系统包括压缩机(C1和C2)、电机(M)和冷却换热器(HE1和HE2);释能子系统包括膨胀机(E1和E2)、发电机(G)和升温换热器(HE3和HE4)。另外,泵(P1和P2)、冷却换热器、升温换热器、热罐(HT)和冷罐(CT)构成蓄热系统。
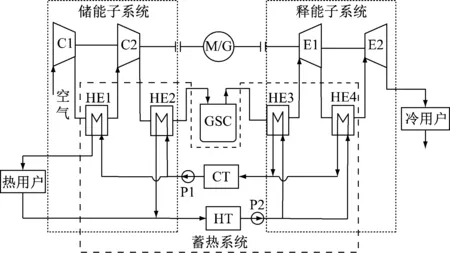
图1 基于AA-CAES的三联产系统示意图Fig.1 Schematic diagram of the tri-generative system based on AA-CAES
系统的运行过程如下:(1)储能阶段,M驱动C1和C2压缩气体工质,一部分从CT流来的蓄热介质在HE1吸收压缩气体的热量供给热用户再存于HT,另一部分在HE2吸收热量后直接存于HT,工质流入储气室(GSC);(2)储释能间隔阶段,压缩气体与GSC壁面存在温差并进行换热;(3)释能阶段,工质流出GSC,蓄热介质被泵出HT,两者在HE3和HE4进行换热,升温后的工质推动E1和E2做功,再带动G发电,E2尾部的低温工质向冷用户输送冷能。
1.2 系统运行方案
为了分析工质和蓄热介质对系统性能的影响,采用以下4种运行方案。
(1)方案1:空气为工质,水为蓄热介质。
(2)方案2:空气为工质,THERMINOL 66为蓄热介质。
(3)方案3:CO2为工质,水为蓄热介质。
(4)方案4:CO2为工质,THERMINOL 66为蓄热介质。
1.3 系统假设
为了便于进行系统性能计算,提出以下假设:(1)工质为理想气体,其比热容是常数;(2)工质与蓄热介质热容量相等;(3)压缩机和膨胀机的等熵效率恒定;(4)忽略储热系统的散热损失以及储气室和管道的泄漏损失。
2 热力学模型
2.1 能量分析
2.1.1 压缩机
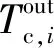
(1)
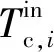
对于单位质量工质,第i级压缩机耗功wc,i为:
(2)
式中:cp,wo为工质比定压热容,J/(kg·K)。
总压缩功Wc为:
Wc=Pctc
(3)
式中:Pc为压缩功率,MW;tc为储能时间,h。
2.1.2 换热器
对于逆流布置的管壳式换热器,其换热器效能ε由式(4)决定:
(4)
式中:NTU为换热器传热单元数;Z为2种介质热容率的比值,设为1。
换热器传热单元数[20]定义为:
(5)
式中:L为换热管长,m;D为换热管直径,m;St1为工质侧斯坦顿数;St2为蓄热介质侧斯坦顿数。
工质流经换热器时会存在压力损失,其压力保持系数Lp[10]为:
(6)
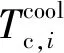
(7)
式中:Tcold为低温蓄热介质温度,K。
输送给热用户的热量Qhe为:
(8)
式中:chsm为蓄热介质比热容,J/(kg·K);qm,c,hsm为储能阶段蓄热介质质量流量,kg/s;t为系统运行时间,h。
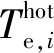
(9)
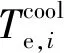
输送给冷用户的冷量Qco为:
(10)
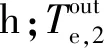
2.1.3 储气室
储能过程中,储气室内压比、温度与时间的关系如下:
(11)
(12)
式中:Tin为储气室进口温度,K;h为对流传热系数,W/(m2·K);Tw为储气室壁面温度,K;cV,wo为工质比定容热容,J/(kg·K);A为储气室表面积,m2;Rg为气体常数,J/(kg·K);β为储气室内压比;V为储气室体积,m3;T为储气室内工质温度,K;qm,c为储气室进口工质质量流量,kg/s;p0为环境压力,Pa。
储释能间隔阶段,储气室内压比和温度随时间的变化可表示为:
(13)
(14)
释能过程中,储气室内压比和温度随时间的变化可表示为:
(15)
(16)
式中:Tout为储气室出口温度,K;qm,e为储气室出口工质质量流量,kg/s。
2.1.4 膨胀机
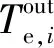
(17)
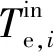
对于单位质量工质,第i级膨胀机耗功we,i为:
(18)
总膨胀功We为:
We=Pete
(19)
式中:Pe为膨胀功率,MW。
(20)
式中:Two为工质温度,K;pwo为工质压力,Pa;qm,wo为工质质量流量,kg/s。
(21)
式中:Thsm为蓄热介质温度,K;phsm为蓄热介质压力,Pa;qm,hsm为蓄热介质质量流量,kg/s。
(22)
(23)
Ex,out,i-Ex,in,i-Wc,i+I=0
(24)
Ex,out,i-Ex,in,i+We,i+I=0
(25)
Ex,out,i-Ex,in,i+I=0
(26)
式中:Ex,out,i为第i级压缩机、膨胀机或部件的出口,J;Ex,in,i为第i级压缩机、膨胀机或部件的进口,J;I为损,J;Wc,i为第i级压缩机功,J。
2.3 系统性能评价指标

(27)
储能密度Den为:
(28)
3 运行结果与分析
3.1 4种方案性能对比分析
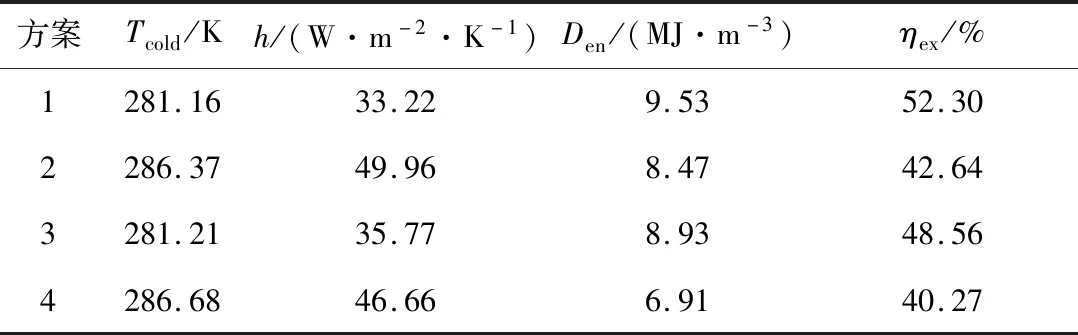
基于AA-CAES的冷热电三联产(CCHP)系统基本运行参数见表1。通过计算,4种运行方案的系统性能如表2所示。方案1的储释能时间、压缩功、膨胀功以及向用户输送的热能/均最大,方案3次之,方案4最小;方案4向冷用户输送的冷量最多,方案2次之,方案1最少。这是因为系统的换热器效能与工质和蓄热介质的种类有关。空气的雷诺数和普朗特数均高于CO2,因此前者的斯坦顿数小于后者。同理,当工质确定时,水的斯坦顿数比THERMINOL 66小。工质侧和蓄热介质侧的斯坦顿数越小,换热器传热单元数越小,换热器效能越大,因此方案1的换热器效能最大。储能过程中,换热器效能增大,蓄热介质吸收的热量随之增加,C2进口温度降低,根据理想气体状态方程,压缩在GSC的工质质量增加,因此充放电时间得以延长。因此,方案1储能过程的压缩功、热量和热均最大。释能过程中,换热器效能增大,蓄热介质返回给工质的热量增加,两级膨胀机进口温度升高,因此方案1的膨胀功最大。然而,膨胀机进口温度升高也会引起E2出口温度与环境温度之差降低,因此方案1的冷量和冷最小。
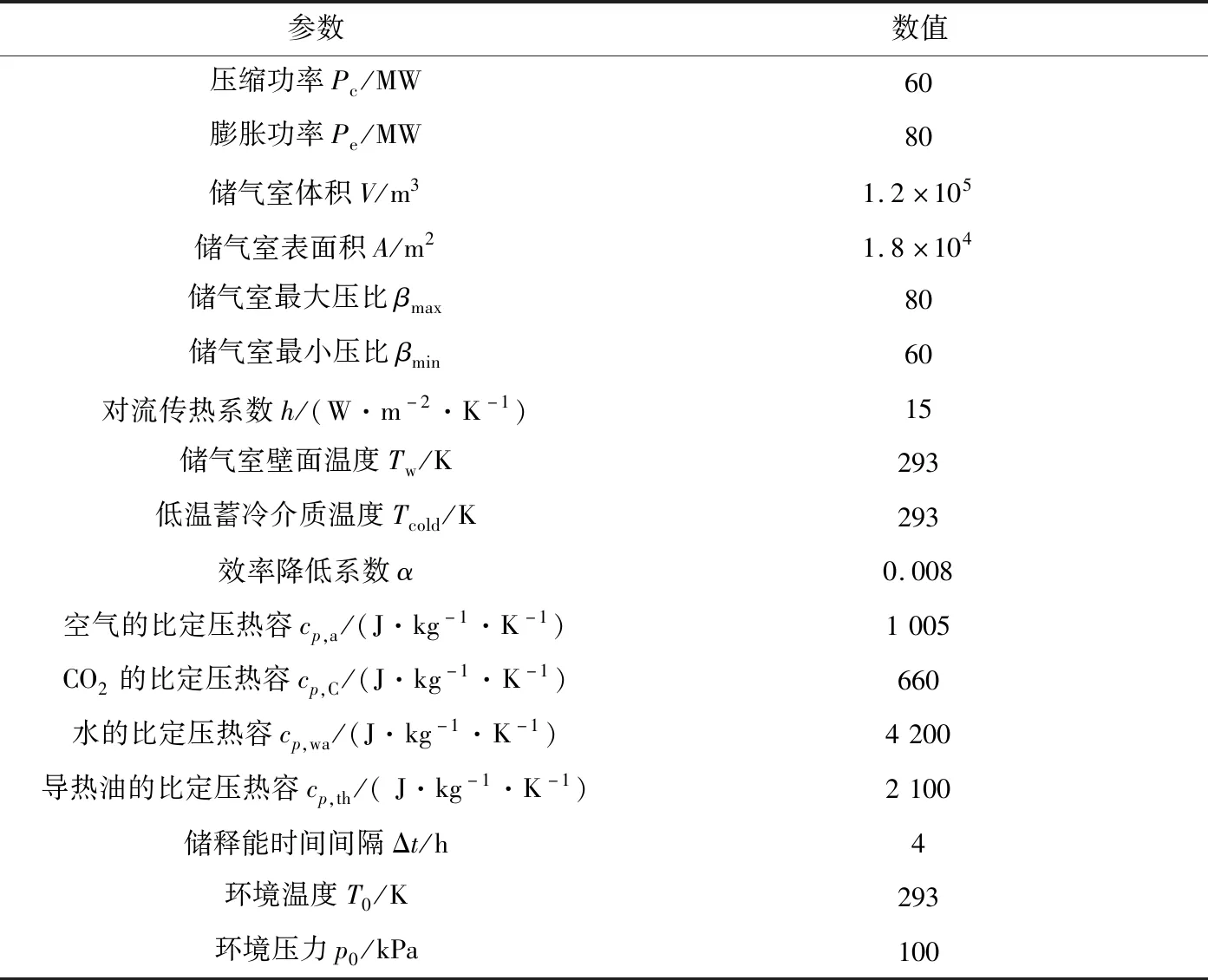
表1 系统基本运行参数Tab.1 Main operating parameters of the system

表2 4种运行方案的系统性能比较Tab.2 Comparison of the system performance of the four operating schemes
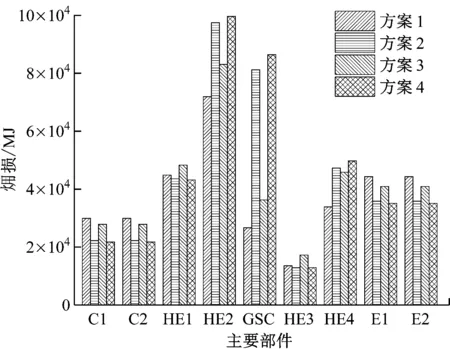
图2 系统主要部件的损Fig.2 Exergy destructions of main components of the system
3.2 低温蓄热介质温度对系统性能的影响
低温蓄热介质温度的变化会影响不同部件的进出口温度,从而导致整个系统的热力学性能发生变化,如图3和图4所示。
从图3和图4可以看出,随着低温蓄冷介质温度的升高,释能过程中膨胀机进口工质温度会有所升高,E2排出的气体与环境的温差降低,对于单位质量工质,系统产生的膨胀功增加,冷量和冷减少。然而,低温蓄冷介质温度的升高将导致GSC进口温度升高,根据理想气体定律,储气总质量会出现下降。在以上因素的综合影响下,系统产生的膨胀功、热量及冷量的总量减少,因此系统的储能密度随之降低。同时系统的膨胀功、热及冷的总量也降低,其降低幅度要小于系统储能阶段压缩机耗功的减少幅度,因此系统的效率随之增加。

图3 低温蓄冷介质温度对效率的影响Fig.3 Influence of the low-temperature cold storage medium temperature on exergy efficiency

图4 低温蓄冷介质温度对储能密度的影响Fig.4 Influence of the low-temperature cold storage medium temperature on energy storage density
3.3 对流传热系数对系统性能的影响
对于不同地质条件的GSC,其内部的对流传热系数变化很大,因而会极大地影响GSC的换热量、充电时间和GSC内工质温度等,进而影响整个系统的性能,如图5和图6所示。
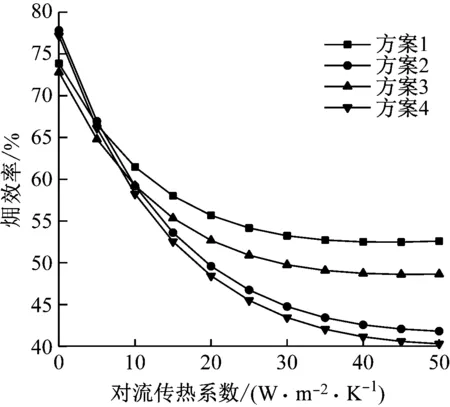
图5 对流传热系数对效率的影响Fig.5 Influence of convective heat transfer coefficient on exergy efficiency
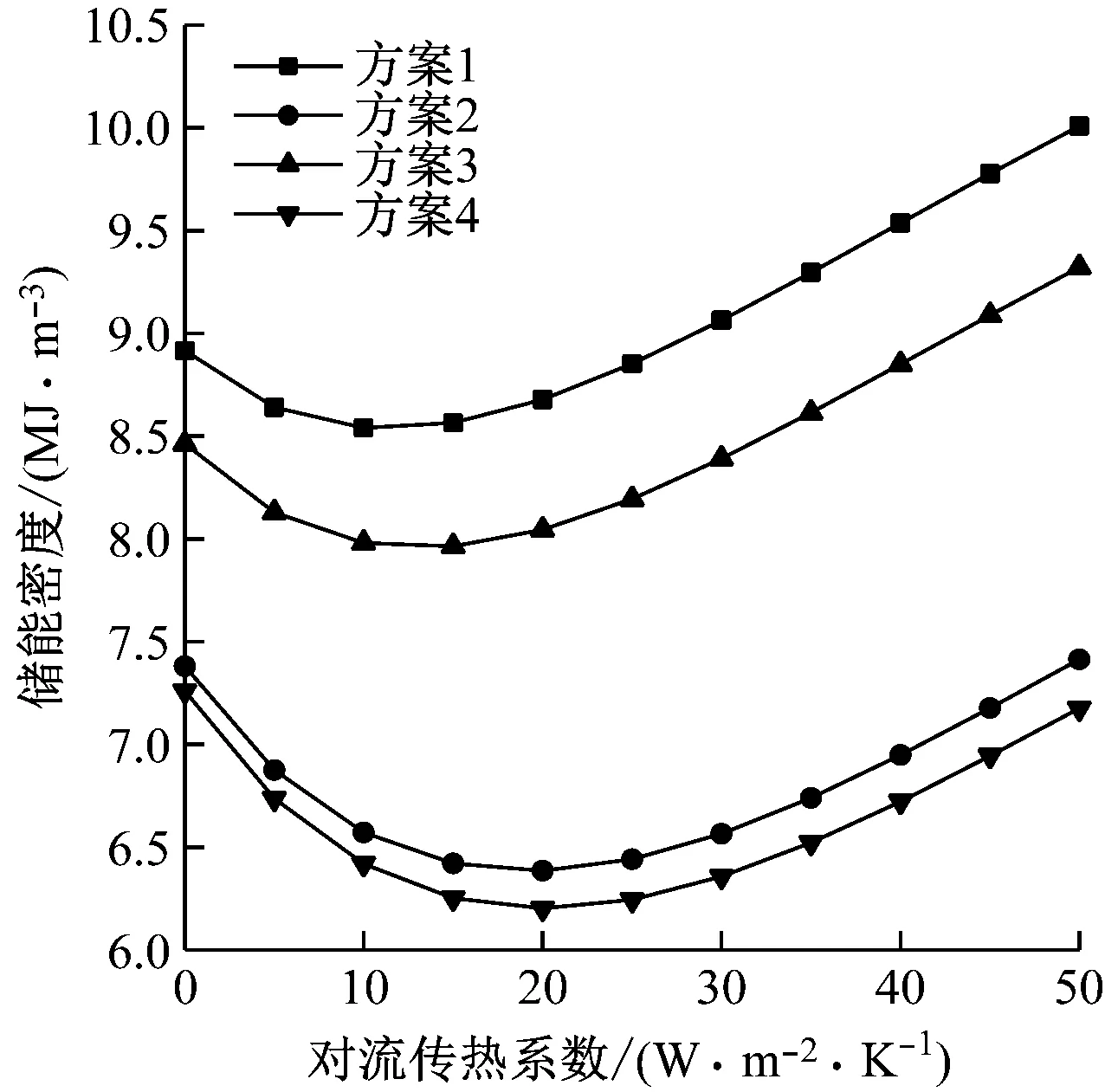
图6 对流传热系数对储能密度的影响Fig.6 Influence of convective heat transfer coefficient on energy storage density
3.4 多目标优化
对系统进行灵敏度分析后发现,低温蓄热介质温度和对流传热系数对系统性能有很大影响,因此采用非支配排序遗传算法(NSGA-II)[21],选择效率和储能密度作为目标函数,低温蓄热介质温度和对流传热系数作为决策变量,对4种运行方案进行多目标优化的范围为:237 K 4种运行方案的帕累托最优解如图7所示。当储能密度降低时,系统的效率增加,系统不能同时获得最大的效率和储能密度。因此,笔者基于优劣解距离法(TOPSIS)计算靠近正理想解和远离负理想解的程度来进行排序,从而选出最终最优解[22],该最优解最接近于正理想解。图中箭头所指即为4种运行方案最终的帕累托最优解。 图7 各个运行方案的帕累托最优解Fig.7 Pareto optimal solution of each scheme 4种运行方案的优化结果如表3所示。由表3可知,方案1~方案4的最优效率分别为52.30%、42.64%、48.56%和40.27%,最优储能密度分别为9.53 MJ/m3、8.47 MJ/m3、8.93 MJ/m3和6.91 MJ/m3。可以看出,4种运行方案的最优储能密度和最优效率的变化趋势与3.1节相同,都是方案1的储能密度和效率最高,方案4最低。从表3还可以看出,当系统采用较低温度的蓄热介质和中等对流传热系数时,可以得到最优储能密度和效率。 表3 4种运行方案的优化结果Tab.3 Optimization results of four opertating schemes (4)当系统采用较低温度的蓄热介质以及中等对流传热系数时,方案1~方案4的最优效率分别为52.30%、42.64%、48.56%和40.27%,最优储能密度分别为9.53 MJ/m3、8.47 MJ/m3、8.93 MJ/m3和6.91 MJ/m3。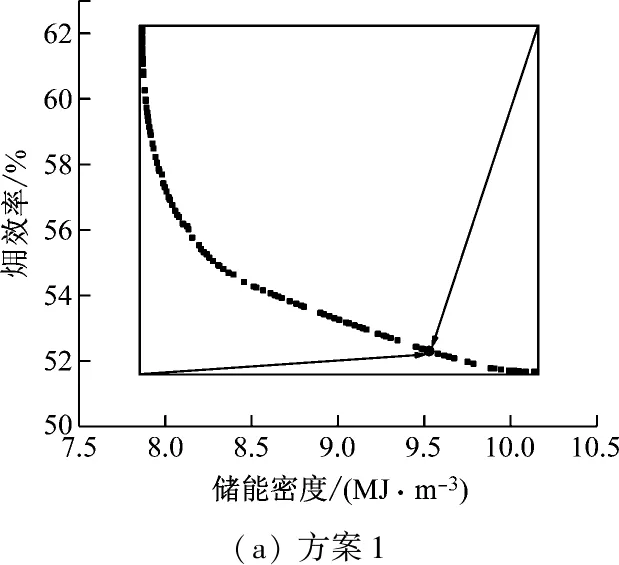
4 结 论

